Sin 18, Cos 18, Tan 18
Sin 18$^0$ = .....
Penyelesaian:
$\begin{align}\sin 36^\circ &= \sin (90^\circ -54^\circ ) \\ \sin 36^\circ &= \cos 54^\circ \\ \sin 36^\circ &= \cos (36^\circ +18^\circ ) \\ \sin 36^\circ &= \cos 36^\circ \cos 18^\circ -\sin 36^\circ \sin 18^\circ \\ 2\sin 18^\circ \cos 18^\circ &= \cos 36^\circ \cos 18^\circ -2\sin 18^\circ \cos 18^\circ \sin 18^\circ \\ 2\sin 18^\circ &= \cos 36^\circ -2{{\sin }^{2}}18^\circ \\ 2\sin 18^\circ &= 1-2{{\sin }^{2}}18^\circ -2{{\sin }^{2}}18^\circ \\ 0 &= -4{{\sin }^{2}}18^\circ -2\sin 18^\circ +1 \\ 0 &= 4{{\sin }^{2}}18^\circ +2\sin 18^\circ -1 \end{align}$
karena $18^\circ $ di kuadran I maka $\sin 18^\circ $ bernilaia positif.
Dengan menggunakan rumus abc maka dari persamaan kuadrat $4{{\sin }^{2}}18^\circ +2\sin 18^\circ -1=0$ diperoleh:
$\begin{align}\sin 18^\circ &= \frac{-2+\sqrt{{{2}^{2}}-4.4.(-1)}}{2.4} \\ &= \frac{-2+\sqrt{20}}{8} \\ &= \frac{-2+2\sqrt{5}}{8} \\ \sin 18^\circ &= \frac{-1+\sqrt{5}}{4} \end{align}$
Untuk menentukan nilai $\cos 18^o$ kita gunakan konsep dasar perbandingan trigonometri seperti berikut ini:
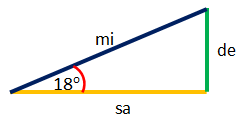
Ingat: $\sin x = \frac{de}{mi}$ maka:
$\sin x = \frac{-1+\sqrt{5}}{4}=\frac{de}{mi}$, diperoleh $de = -1 +\sqrt{5}$ dan $mi = 4$, dengan menggunakan teorema phythagoras
$sa =\sqrt{mi^2 - de^2}$
$sa = \sqrt{4^2 - (-1 + \sqrt{5})^2}$
$sa = \sqrt{10 + 2\sqrt{5}}$
$\cos 18^o = \frac{sa}{mi}$
$\cos 18^o = \frac{\sqrt{10+2\sqrt{5}}}{4}$
Sedangkan untuk nilai $\tan 18^o$ kita gunakan: $\tan x = \frac{\sin x}{\cos x}$, diperoleh:
$\tan 18^o = \frac{\sin 18^o}{\cos 18^o}$
$\tan 18^o = \frac{-1 + \sqrt{5}}{\sqrt{10 + 2\sqrt{5}}}$
Penyelesaian:
$\begin{align}\sin 36^\circ &= \sin (90^\circ -54^\circ ) \\ \sin 36^\circ &= \cos 54^\circ \\ \sin 36^\circ &= \cos (36^\circ +18^\circ ) \\ \sin 36^\circ &= \cos 36^\circ \cos 18^\circ -\sin 36^\circ \sin 18^\circ \\ 2\sin 18^\circ \cos 18^\circ &= \cos 36^\circ \cos 18^\circ -2\sin 18^\circ \cos 18^\circ \sin 18^\circ \\ 2\sin 18^\circ &= \cos 36^\circ -2{{\sin }^{2}}18^\circ \\ 2\sin 18^\circ &= 1-2{{\sin }^{2}}18^\circ -2{{\sin }^{2}}18^\circ \\ 0 &= -4{{\sin }^{2}}18^\circ -2\sin 18^\circ +1 \\ 0 &= 4{{\sin }^{2}}18^\circ +2\sin 18^\circ -1 \end{align}$
karena $18^\circ $ di kuadran I maka $\sin 18^\circ $ bernilaia positif.
Dengan menggunakan rumus abc maka dari persamaan kuadrat $4{{\sin }^{2}}18^\circ +2\sin 18^\circ -1=0$ diperoleh:
$\begin{align}\sin 18^\circ &= \frac{-2+\sqrt{{{2}^{2}}-4.4.(-1)}}{2.4} \\ &= \frac{-2+\sqrt{20}}{8} \\ &= \frac{-2+2\sqrt{5}}{8} \\ \sin 18^\circ &= \frac{-1+\sqrt{5}}{4} \end{align}$
Untuk menentukan nilai $\cos 18^o$ kita gunakan konsep dasar perbandingan trigonometri seperti berikut ini:
Ingat: $\sin x = \frac{de}{mi}$ maka:
$\sin x = \frac{-1+\sqrt{5}}{4}=\frac{de}{mi}$, diperoleh $de = -1 +\sqrt{5}$ dan $mi = 4$, dengan menggunakan teorema phythagoras
$sa =\sqrt{mi^2 - de^2}$
$sa = \sqrt{4^2 - (-1 + \sqrt{5})^2}$
$sa = \sqrt{10 + 2\sqrt{5}}$
$\cos 18^o = \frac{sa}{mi}$
$\cos 18^o = \frac{\sqrt{10+2\sqrt{5}}}{4}$
Sedangkan untuk nilai $\tan 18^o$ kita gunakan: $\tan x = \frac{\sin x}{\cos x}$, diperoleh:
$\tan 18^o = \frac{\sin 18^o}{\cos 18^o}$
$\tan 18^o = \frac{-1 + \sqrt{5}}{\sqrt{10 + 2\sqrt{5}}}$
Semoga postingan: Sin 18, Cos 18, Tan 18 ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.
Post a Comment for "Sin 18, Cos 18, Tan 18"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.