Soal dan Pembahasan Matematika IPA SBMPTN 2018 Kode 402
SBMPTN 2018 Matematika IPA Kode 402 No. 1
Jika fungsi $f(x)=a^2\sin (ax) + 10$ mempunyai periode $\frac{\pi}{2}$, maka nilai minimum fungsi $f$ adalah ...
A. -16 B. -6 C. 1 D. 6 E. 9
Pembahasan:
Dari fungsi $f(x)=a^2\sin (ax) + 10$ diperoleh periode (p) = $\frac{2\pi }{a}$, maka:
$\frac{2\pi }{a}=\frac{\pi }{2}\Leftrightarrow a\pi =4\pi \Leftrightarrow a=4$,
$f(x)=a^2\sin (ax) + 10$
$f(x)=16\sin 4x+10$, nilai fungsi $f$minimum jika $\sin 4x=-1$, diperoleh:
$f(x)=16.(-1)+10$
$f(x)=-6$
Kunci: B
Pembahasan:
Dari fungsi $f(x)=a^2\sin (ax) + 10$ diperoleh periode (p) = $\frac{2\pi }{a}$, maka:
$\frac{2\pi }{a}=\frac{\pi }{2}\Leftrightarrow a\pi =4\pi \Leftrightarrow a=4$,
$f(x)=a^2\sin (ax) + 10$
$f(x)=16\sin 4x+10$, nilai fungsi $f$minimum jika $\sin 4x=-1$, diperoleh:
$f(x)=16.(-1)+10$
$f(x)=-6$
Kunci: B
SBMPTN 2018 Matematika IPA Kode 402 No. 2
Jika titik $P(-1,3)$ digeser sejauh $a$ satuan ke kanan dan $b$ satuan ke bawah lalu dicerminkan ke garis $x=2$, maka bayangannya adalah $P'(3,-6)$. Nilai $a-b$ adalah ..
A. -1 B. -3 C. -5 D. -7 E. -9
Pembahasan:
Permasalahan di atas menggunakan translasi.
$P(-1,3)\xrightarrow{\left( \begin{matrix} a \\ -b \\ \end{matrix} \right)}P'(-1+a,3-b)$
$P'(-1+a,3-b)$ dicerminkan ke garis $x=2$ menghasilkan:
$P''(2.2-(-1+a),3-b)=P''(3,-6)$
$P''(5-a,3-b)=P''(3,-6)$
$5-a=3\Leftrightarrow a=2$
$3-b=-6\Leftrightarrow b=9$
Maka: $a-b=2-9=-7$
Kunci: D
Pembahasan:
Permasalahan di atas menggunakan translasi.
$P(-1,3)\xrightarrow{\left( \begin{matrix} a \\ -b \\ \end{matrix} \right)}P'(-1+a,3-b)$
$P'(-1+a,3-b)$ dicerminkan ke garis $x=2$ menghasilkan:
$P''(2.2-(-1+a),3-b)=P''(3,-6)$
$P''(5-a,3-b)=P''(3,-6)$
$5-a=3\Leftrightarrow a=2$
$3-b=-6\Leftrightarrow b=9$
Maka: $a-b=2-9=-7$
Kunci: D
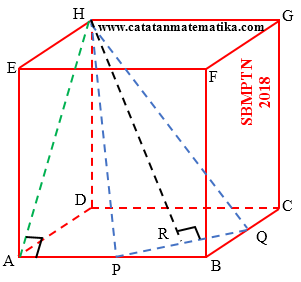
SBMPTN 2018 Matematika IPA Kode 402 No. 3
Diketahui kubus ABCD.EFGH dengan panjang rusuk $2\sqrt{2}$ cm. Jika titik $P$ ditengah-tengah AB dan titik Q ditengah-tengah BC, maka jarak antara titik H dengan garis PQ adalah ... cm.
A. $\sqrt{15}$ B. 4 C. $\sqrt{17}$ D. $3\sqrt{2}$ E. $\sqrt{19}$
Pembahasan:
$AB=2\sqrt{2}\Rightarrow PB=\sqrt{2}$
$BC=2\sqrt{2}\Rightarrow BQ=\sqrt{2}$
$PQ=\sqrt{P{{B}^{2}}+B{{Q}^{2}}}\Leftrightarrow PQ=2$
Perhatikan segitiga HAP siku-siku di titik A, $AP=\sqrt{2}$, $AH=4$, maka:
$HP=\sqrt{A{{H}^{2}}+A{{P}^{2}}}$
$HP=\sqrt{{{4}^{2}}+{{(\sqrt{2})}^{2}}}$
$HP=3\sqrt{2}$, $HP=HQ$
Maka garis tinggi HR membagi dua PQ, sehingga $PR=\frac{1}{2}PQ=1$
jarak antara titik H dengan garis PQ adalah panjang HR.
Perhatikan segitiga PRH siku-siku di titik R, maka:
$HR=\sqrt{H{{P}^{2}}+P{{R}^{2}}}$
$HR=\sqrt{{{(3\sqrt{2})}^{2}}-{{1}^{2}}}$
$HR=\sqrt{17}$
Kunci: C
SBMPTN 2018 Matematika IPA Kode 402 No. 4
$\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin (x)\cos (x)}{\sqrt{\pi +2\sin (x)}-\sqrt{\pi }}=...$ A. $-2\sqrt{\pi }$ B. $-\sqrt{\pi }$ C. 0 D. $\sqrt{\pi }$ E. $2\sqrt{\pi }$
Pembahasan:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin (x)\cos (x)}{\sqrt{\pi +2\sin (x)}-\sqrt{\pi }}=...$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{\frac{1}{2} \sin 2x}{\sqrt{\pi +2\sin (x)}-\sqrt{\pi }}$ (gunakan dalil L’Hopital)
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{\frac{1}{2}.2\cos 2x}{\frac{2\cos x}{2\sqrt{\pi +2\sin x}}}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{\cos 2x.\sqrt{\pi +2\sin x}}{\cos x}$
$=\frac{\cos 2.0.\sqrt{\pi +2\sin 0}}{\cos 0}$
$=\sqrt{\pi }$
Kunci: D
SBMPTN 2018 Matematika IPA Kode 402 No. 5
Diketahui barisan geometri $U_n$, dengan $U_2+1$ adalah rata-rata $U_1$ dan $U_3$. Jika $U_1=8$, maka jumlah 4 suku pertama yang mungkin adalah ...
A. 15 B. 20 C. 25 D. 30 E. 35
Pembahasan:
Barisan Geometri: ${{U}_{n}}=a{{r}^{n-1}}$
${{U}_{2}}+1=\frac{{{U}_{1}}+{{U}_{3}}}{2}$
$ar+1=\frac{a+a{{r}^{2}}}{2}$
$2ar+2=a+a{{r}^{2}}$
$2.8.r+2=8+8.{{r}^{2}}$
$8{{r}^{2}}-16r+6=0$
$4{{r}^{2}}-8r+3=0$
$(2r-1)(2r-3)=0$
$r=\frac{1}{2}$ atau $r=\frac{3}{2}$
${{S}_{n}}=\frac{a({{r}^{n}}-1)}{r-1}$
$r=\frac{1}{2}\Rightarrow {{S}_{4}}=\frac{8\left( \frac{1}{16}-1 \right)}{\frac{1}{2}-1}=15$
Kunci: A
SBMPTN 2018 Matematika IPA Kode 402 No. 6
Daerah $R$ dibatasi oleh $y=bx^4$, $y=b$, $x=2$, dan garis sumbu $x$ positif, dengan $b > 0$. Jika volume benda padat yang didapat dengan memutar $R$ terhadap sumbu $x$ adalah $\frac{10}{9}\pi$, maka $b$ = ...
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan: -
Kunci: A
SBMPTN 2018 Matematika IPA Kode 402 No. 7
Ari dan Ira merupakan anggota dari suatu kelompok yang terdiri dari 9 orang. Banyaknya cara membuat barisan, dengan syarat Ari dan Ira tidak berdampingan, adalah ...
A. $7 \times 8!$ B. $6 \times 8!$ C. $5 \times 8!$ D. $7 \times 7!$ E. $6 \times 7!$
Pembahasan:
Banyak barisan 9 orang secara bebas = 9!
Banyak barisan dengan Ari dan Ira berdampingan = 2!8!
Banyak barisan dengan Ari dan Ira tidak berdampingan adalah:
= 9! – 2!8!
= 9.8! – 2.8!
= 7 x 8!
Kunci: A
SBMPTN 2018 Matematika IPA Kode 402 No. 8
Jika panjang jari-jari lingkaran $x^2 + y^2 + Ax + 2Ay+C=0$ dan $x^2+y^2+Ax+3Ay+C=0$ berturut-turut adalah 2 dan $\sqrt{10}$, maka nilai C adalah ...
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan:
Teori: ${{x}^{2}}+{{y}^{2}}+Ax+By+C=0$ maka $r=\sqrt{\frac{{{A}^{2}}+{{B}^{2}}-4C}{4}}$
$x^2 + y^2 + Ax + 2Ay+C=0$, r = 2 maka:
$2=\sqrt{\frac{{{A}^{2}}+4{{A}^{2}}-4C}{4}}$
$4=\frac{5{{A}^{2}}-4C}{4}$
$5{{A}^{2}}-4C=16$ persamaan 1)
$x^2+y^2+Ax+3Ay+C=0$; r = $\sqrt{10}$ maka:
$\sqrt{10}=\sqrt{\frac{{{A}^{2}}+9{{A}^{2}}-4C}{4}}$
$10=\frac{10{{A}^{2}}-4C}{4}$
$10{{A}^{2}}-4C=40$
$5{{A}^{2}}-2C=20$… persamaan 2)
Eliminasi ${{A}^{2}}$ sehingga dengan persamaan 1) dikurang persamaan 2) diperoleh:
$-2C=-4\Leftrightarrow C=2$
Kunci: B
SBMPTN 2018 Matematika IPA Kode 402 No. 9
Sisa pembagian $p(x)=x^3+Ax^2+Bx+C$ oleh $x+3$ adalah 2. Jika $p(x)$ habis dibagi oleh $x+1$ dan $x-1$, maka $A+2B-3C$ = ...
A. 10 B. 11 C. 12 D. 13 E. 14
Pembahasan:
$p(x)=x^3+Ax^2+Bx+C$ dibagi $x+3$ sisa 2, maka: $p(-3)=2$
$p(-3)={{(-3)}^{3}}+A{{(-3)}^{2}}+B(-3)+C=2$
$-27+9A-3B+C=2$
$9A-3B+C=29$… persamaan 1
$p(x)=x^3+Ax^2+Bx+C$ habis dibagi oleh $x+1$ dan $x-1$, maka $p(-1)=0$ dan $p(1)=0$
$p(-1)={{(-1)}^{3}}+A{{(-1)}^{2}}+B(-1)+C=0$
$A-B+C=1$… persamaan 2
$p(1)={{1}^{3}}+A{{.1}^{2}}+B.1+C$
$A+B+C=-1$… persamaan 3
Dari persamaan 1) dan 2) eliminasi C dengan mengurangkan kedua persamaan tersebut, diperoleh:
$8A-2B=28$… persamaan 4
Dari persamaan 1) dan 3) eliminasi C dengan mengurangkan kedua persamaan tersebut, diperoleh:
$8A-4B=30$… persamaan 5
Dari persamaan 4) dan 5) eliminasi A dengan mengurangkan kedua persamaan tersebut, diperoleh:
$2B=-2\Leftrightarrow B=-1$ substitusi ke persamaan 4)
$8A-2B=28$
$8A+2=28\Leftrightarrow A=\frac{26}{8}=\frac{13}{4}$, substitusi ke persamaan 2)
$A-B+C=1$
$\frac{13}{4}+1+C=1\Leftrightarrow C=-\frac{13}{4}$
$A+2B-3C=\frac{13}{4}+2.(-1)-3.\left( -\frac{13}{4} \right)$
$A+2B-3C=11$
Kunci: B
SBMPTN 2018 Matematika IPA Kode 402 No. 10
Garis yang melalui titik O(0,0) dan P(a,b) berpotongan tegak lurus dengan garis singgung kurva $y=\frac{9}{2}-x^2$ di P(a,b). Jika titik P berada di kuadran II, maka $a+b$ adalah ...
A. $-\frac{3}{2}$
B. $-\frac{27}{50}$
C. $\frac{6-\sqrt{6}}{2}$
D. $\frac{8-\sqrt{2}}{2}$
E. $\frac{15-2\sqrt{3}}{4}$
Pembahasan:
Gradien garis melalui titik O(0,0) dan P(a,b) adalah ${{m}_{1}}=\frac{b}{a}$
Gradien garis singgung kurva $y=\frac{9}{2}-x^2$ di titik P(a,b) adalah:
$\frac{dy}{dx}=-2x$
${{m}_{2}}={{\left. \frac{dy}{dx} \right|}_{x=a}}=-2a$
Syarat tegak lurus:
${{m}_{1}}.{{m}_{2}}=-1$
$\frac{b}{a}.(-2a)=-1\Leftrightarrow b=\frac{1}{2}$
P(a,b) berada pada kurva$y=\frac{9}{2}-x^2$, maka:
$b=\frac{9}{2}-{{a}^{2}}$
$\frac{1}{2}=\frac{9}{2}-{{a}^{2}}$
${{a}^{2}}=4$
$a=\pm 2$, karena titik P(a,b) berada pada kuadran II maka $a=-2$
$a+b=-2+\frac{1}{2}=-\frac{3}{2}$
Kunci: A
SBMPTN 2018 Matematika IPA Kode 402 No. 11
$\int\limits_{1/8}^{1/3}{\frac{3}{{{x}^{2}}}\sqrt{1+\frac{1}{x}}dx}$
A. 19 B. 38 C. 57 D. 76 E. 95
Pembahasan:
$\int\limits_{1/8}^{1/3}{\frac{3}{{{x}^{2}}}\sqrt{1+\frac{1}{x}}dx}=\int\limits_{1/8}^{1/3}{\frac{3}{{{x}^{2}}}{{\left( 1+\frac{1}{x} \right)}^{\frac{1}{2}}}dx}$
$=\left. \frac{1}{\frac{1}{2}+1}.{{\left( 1+\frac{1}{x} \right)}^{\frac{1}{2}+1}}.\frac{{}^{3}/{}_{{{x}^{2}}}}{{}^{-1}/{}_{{{x}^{2}}}} \right|_{1/8}^{1/3}$
$=\left. \frac{2}{3}.\left( 1+\frac{1}{x} \right)\sqrt{1+\frac{1}{x}}.(-3) \right|_{1/8}^{1/3}$
$=\left. -2\left( 1+\frac{1}{x} \right)\sqrt{1+\frac{1}{x}} \right|_{1/8}^{1/3}$
$=-2\left( 1+\frac{1}{1/3} \right)\sqrt{1+\frac{1}{1/3}}-\left[ -2\left( 1+\frac{1}{1/8} \right)\sqrt{1+\frac{1}{1/8}} \right]$
$=-2.4.2+2.9.3$
$=38$
Kunci: B
Diketahui barisan geometri $U_n$, dengan $U_2+1$ adalah rata-rata $U_1$ dan $U_3$. Jika $U_1=8$, maka jumlah 4 suku pertama yang mungkin adalah ...
A. 15 B. 20 C. 25 D. 30 E. 35
Pembahasan:
Barisan Geometri: ${{U}_{n}}=a{{r}^{n-1}}$
${{U}_{2}}+1=\frac{{{U}_{1}}+{{U}_{3}}}{2}$
$ar+1=\frac{a+a{{r}^{2}}}{2}$
$2ar+2=a+a{{r}^{2}}$
$2.8.r+2=8+8.{{r}^{2}}$
$8{{r}^{2}}-16r+6=0$
$4{{r}^{2}}-8r+3=0$
$(2r-1)(2r-3)=0$
$r=\frac{1}{2}$ atau $r=\frac{3}{2}$
${{S}_{n}}=\frac{a({{r}^{n}}-1)}{r-1}$
$r=\frac{1}{2}\Rightarrow {{S}_{4}}=\frac{8\left( \frac{1}{16}-1 \right)}{\frac{1}{2}-1}=15$
Kunci: A
SBMPTN 2018 Matematika IPA Kode 402 No. 6
Daerah $R$ dibatasi oleh $y=bx^4$, $y=b$, $x=2$, dan garis sumbu $x$ positif, dengan $b > 0$. Jika volume benda padat yang didapat dengan memutar $R$ terhadap sumbu $x$ adalah $\frac{10}{9}\pi$, maka $b$ = ...
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan: -
Kunci: A
SBMPTN 2018 Matematika IPA Kode 402 No. 7
Ari dan Ira merupakan anggota dari suatu kelompok yang terdiri dari 9 orang. Banyaknya cara membuat barisan, dengan syarat Ari dan Ira tidak berdampingan, adalah ...
A. $7 \times 8!$ B. $6 \times 8!$ C. $5 \times 8!$ D. $7 \times 7!$ E. $6 \times 7!$
Pembahasan:
Banyak barisan 9 orang secara bebas = 9!
Banyak barisan dengan Ari dan Ira berdampingan = 2!8!
Banyak barisan dengan Ari dan Ira tidak berdampingan adalah:
= 9! – 2!8!
= 9.8! – 2.8!
= 7 x 8!
Kunci: A
SBMPTN 2018 Matematika IPA Kode 402 No. 8
Jika panjang jari-jari lingkaran $x^2 + y^2 + Ax + 2Ay+C=0$ dan $x^2+y^2+Ax+3Ay+C=0$ berturut-turut adalah 2 dan $\sqrt{10}$, maka nilai C adalah ...
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan:
Teori: ${{x}^{2}}+{{y}^{2}}+Ax+By+C=0$ maka $r=\sqrt{\frac{{{A}^{2}}+{{B}^{2}}-4C}{4}}$
$x^2 + y^2 + Ax + 2Ay+C=0$, r = 2 maka:
$2=\sqrt{\frac{{{A}^{2}}+4{{A}^{2}}-4C}{4}}$
$4=\frac{5{{A}^{2}}-4C}{4}$
$5{{A}^{2}}-4C=16$ persamaan 1)
$x^2+y^2+Ax+3Ay+C=0$; r = $\sqrt{10}$ maka:
$\sqrt{10}=\sqrt{\frac{{{A}^{2}}+9{{A}^{2}}-4C}{4}}$
$10=\frac{10{{A}^{2}}-4C}{4}$
$10{{A}^{2}}-4C=40$
$5{{A}^{2}}-2C=20$… persamaan 2)
Eliminasi ${{A}^{2}}$ sehingga dengan persamaan 1) dikurang persamaan 2) diperoleh:
$-2C=-4\Leftrightarrow C=2$
Kunci: B
SBMPTN 2018 Matematika IPA Kode 402 No. 9
Sisa pembagian $p(x)=x^3+Ax^2+Bx+C$ oleh $x+3$ adalah 2. Jika $p(x)$ habis dibagi oleh $x+1$ dan $x-1$, maka $A+2B-3C$ = ...
A. 10 B. 11 C. 12 D. 13 E. 14
Pembahasan:
$p(x)=x^3+Ax^2+Bx+C$ dibagi $x+3$ sisa 2, maka: $p(-3)=2$
$p(-3)={{(-3)}^{3}}+A{{(-3)}^{2}}+B(-3)+C=2$
$-27+9A-3B+C=2$
$9A-3B+C=29$… persamaan 1
$p(x)=x^3+Ax^2+Bx+C$ habis dibagi oleh $x+1$ dan $x-1$, maka $p(-1)=0$ dan $p(1)=0$
$p(-1)={{(-1)}^{3}}+A{{(-1)}^{2}}+B(-1)+C=0$
$A-B+C=1$… persamaan 2
$p(1)={{1}^{3}}+A{{.1}^{2}}+B.1+C$
$A+B+C=-1$… persamaan 3
Dari persamaan 1) dan 2) eliminasi C dengan mengurangkan kedua persamaan tersebut, diperoleh:
$8A-2B=28$… persamaan 4
Dari persamaan 1) dan 3) eliminasi C dengan mengurangkan kedua persamaan tersebut, diperoleh:
$8A-4B=30$… persamaan 5
Dari persamaan 4) dan 5) eliminasi A dengan mengurangkan kedua persamaan tersebut, diperoleh:
$2B=-2\Leftrightarrow B=-1$ substitusi ke persamaan 4)
$8A-2B=28$
$8A+2=28\Leftrightarrow A=\frac{26}{8}=\frac{13}{4}$, substitusi ke persamaan 2)
$A-B+C=1$
$\frac{13}{4}+1+C=1\Leftrightarrow C=-\frac{13}{4}$
$A+2B-3C=\frac{13}{4}+2.(-1)-3.\left( -\frac{13}{4} \right)$
$A+2B-3C=11$
Kunci: B
SBMPTN 2018 Matematika IPA Kode 402 No. 10
Garis yang melalui titik O(0,0) dan P(a,b) berpotongan tegak lurus dengan garis singgung kurva $y=\frac{9}{2}-x^2$ di P(a,b). Jika titik P berada di kuadran II, maka $a+b$ adalah ...
A. $-\frac{3}{2}$
B. $-\frac{27}{50}$
C. $\frac{6-\sqrt{6}}{2}$
D. $\frac{8-\sqrt{2}}{2}$
E. $\frac{15-2\sqrt{3}}{4}$
Pembahasan:
Gradien garis melalui titik O(0,0) dan P(a,b) adalah ${{m}_{1}}=\frac{b}{a}$
Gradien garis singgung kurva $y=\frac{9}{2}-x^2$ di titik P(a,b) adalah:
$\frac{dy}{dx}=-2x$
${{m}_{2}}={{\left. \frac{dy}{dx} \right|}_{x=a}}=-2a$
Syarat tegak lurus:
${{m}_{1}}.{{m}_{2}}=-1$
$\frac{b}{a}.(-2a)=-1\Leftrightarrow b=\frac{1}{2}$
P(a,b) berada pada kurva$y=\frac{9}{2}-x^2$, maka:
$b=\frac{9}{2}-{{a}^{2}}$
$\frac{1}{2}=\frac{9}{2}-{{a}^{2}}$
${{a}^{2}}=4$
$a=\pm 2$, karena titik P(a,b) berada pada kuadran II maka $a=-2$
$a+b=-2+\frac{1}{2}=-\frac{3}{2}$
Kunci: A
SBMPTN 2018 Matematika IPA Kode 402 No. 11
$\int\limits_{1/8}^{1/3}{\frac{3}{{{x}^{2}}}\sqrt{1+\frac{1}{x}}dx}$
A. 19 B. 38 C. 57 D. 76 E. 95
Pembahasan:
$\int\limits_{1/8}^{1/3}{\frac{3}{{{x}^{2}}}\sqrt{1+\frac{1}{x}}dx}=\int\limits_{1/8}^{1/3}{\frac{3}{{{x}^{2}}}{{\left( 1+\frac{1}{x} \right)}^{\frac{1}{2}}}dx}$
$=\left. \frac{1}{\frac{1}{2}+1}.{{\left( 1+\frac{1}{x} \right)}^{\frac{1}{2}+1}}.\frac{{}^{3}/{}_{{{x}^{2}}}}{{}^{-1}/{}_{{{x}^{2}}}} \right|_{1/8}^{1/3}$
$=\left. \frac{2}{3}.\left( 1+\frac{1}{x} \right)\sqrt{1+\frac{1}{x}}.(-3) \right|_{1/8}^{1/3}$
$=\left. -2\left( 1+\frac{1}{x} \right)\sqrt{1+\frac{1}{x}} \right|_{1/8}^{1/3}$
$=-2\left( 1+\frac{1}{1/3} \right)\sqrt{1+\frac{1}{1/3}}-\left[ -2\left( 1+\frac{1}{1/8} \right)\sqrt{1+\frac{1}{1/8}} \right]$
$=-2.4.2+2.9.3$
$=38$
Kunci: B
SBMPTN 2018 Matematika IPA Kode 402 No. 12
Diketahui $(a_n)$ dan $(b_n)$ adalah dua barisan aritmetika dengan $a_1=5$, $a_2=8$, $b_1=3$, dan $b_2=7$. Jika A = {$a_1$, $a_2$, ..., $a_{100}$} dan B = {$b_1$, $b_2$, ..., $b_{100}$}, maka banyaknya anggota $A\cap B$ adalah ...
A. 20 B. 21 C. 22 D. 23 E. 24
Pembahasan:
$a_1=5$, $a_2=8$, b = 8 – 5 = 3, maka:
$b_1=3$, $b_2=7$, b = 7 – 3 = 4, maka:
A = {5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38, 41, 44, 47
B = {3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47
Jika diperhatikan polanya maka:
$A\cap B$ = {${{a}_{3}}$, ${{a}_{7}}$, ${{a}_{11}}$, …, ${{a}_{n}}$}
Membentuk barisan aritmetika:
3, 7, 11, …, ${{U}_{n}}$
${{U}_{n}}=4n-1\le 100\Leftrightarrow n=25$
Jadi banyak anggota $A\cap B$ adalah 25.
Kunci: Tidak ada opsi
$a_1=5$, $a_2=8$, b = 8 – 5 = 3, maka:
$b_1=3$, $b_2=7$, b = 7 – 3 = 4, maka:
A = {5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38, 41, 44, 47
B = {3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47
Jika diperhatikan polanya maka:
$A\cap B$ = {${{a}_{3}}$, ${{a}_{7}}$, ${{a}_{11}}$, …, ${{a}_{n}}$}
Membentuk barisan aritmetika:
3, 7, 11, …, ${{U}_{n}}$
${{U}_{n}}=4n-1\le 100\Leftrightarrow n=25$
Jadi banyak anggota $A\cap B$ adalah 25.
Kunci: Tidak ada opsi
SBMPTN 2018 Matematika IPA Kode 402 No. 13
Himpunan semua bilangan real $x$ pada selang $[\pi,2\pi]$ yang memenuhi $2\cos \text{ }\left( \frac{\pi }{2}-x \right)\text{ }\cos x\ge 1-\cos 2x$ berbentuk $[a,b]$. Nilai $a+b$ adalah ...
A. $\frac{9\pi}{4}$
B. $3\pi$
C. $\frac{13\pi}{4}$
D. $\frac{14\pi}{4}$
E. $\frac{15\pi}{4}$
Pembahasan:
$2\cos \text{ }\left( \frac{\pi }{2}-x \right)\text{ }\cos x\ge 1-\cos 2x$
$2\sin x\cos x\ge 1-\cos 2x$
$2\sin x\cos x\ge 2{{\sin }^{2}}x$
$\sin x\cos x\ge {{\sin }^{2}}x$
${{\sin }^{2}}x-\sin x\cos x\le 0$
$\sin x(1-\cos x)\le 0$
Karena $1-\cos x\ge 0$, maka $\sin x\le 0$ ini dipenuhi pada kuadran ketiga dan keempat yaitu pada selang $[\pi ,2\pi ]=[a,b]$ maka $a+b=\pi +2\pi =3\pi $
Kunci: B
Pembahasan:
$2\cos \text{ }\left( \frac{\pi }{2}-x \right)\text{ }\cos x\ge 1-\cos 2x$
$2\sin x\cos x\ge 1-\cos 2x$
$2\sin x\cos x\ge 2{{\sin }^{2}}x$
$\sin x\cos x\ge {{\sin }^{2}}x$
${{\sin }^{2}}x-\sin x\cos x\le 0$
$\sin x(1-\cos x)\le 0$
Karena $1-\cos x\ge 0$, maka $\sin x\le 0$ ini dipenuhi pada kuadran ketiga dan keempat yaitu pada selang $[\pi ,2\pi ]=[a,b]$ maka $a+b=\pi +2\pi =3\pi $
Kunci: B
SBMPTN 2018 Matematika IPA Kode 402 No. 14
Diketahui $f(x)=9^{x^2-x+2}$ dan $g(x)=3^{x^2+2x+1}$. Jika $(a,b)$ adalah interval dengan grafik $y=f(x)$ berada di bawah grafik $y=g(x)$, maka nilai $a+2b$ adalah ...
A. 2 B. 4 C. 5 D. 7 E. 9
Pembahasan:
$y=f(x)$ berada di bawah grafik $y=g(x)$, maka:
$f(x)
${{9}^{{{x}^{2}}-x+2}} < {{3}^{{{x}^{2}}+2x+1}}$
${{\left( {{3}^{2}} \right)}^{{{x}^{2}}-x+2}} < {{3}^{{{x}^{2}}+2x+1}}$
${{3}^{2{{x}^{2}}-2x+4}} < {{3}^{{{x}^{2}}+2x+1}}$
$2{{x}^{2}}-2x+4 < {{x}^{2}}+2x+1$
${{x}^{2}}-4x+3 < 0$
$(x-1)(x-3) < 0$
$x=1$ atau $x=3$
$1 < x < 3$maka $a=1$ dan $b=3$
Maka: $a+2b=1+2.3=7$
Kunci: D
$y=f(x)$ berada di bawah grafik $y=g(x)$, maka:
$f(x)
${{9}^{{{x}^{2}}-x+2}} < {{3}^{{{x}^{2}}+2x+1}}$
${{\left( {{3}^{2}} \right)}^{{{x}^{2}}-x+2}} < {{3}^{{{x}^{2}}+2x+1}}$
${{3}^{2{{x}^{2}}-2x+4}} < {{3}^{{{x}^{2}}+2x+1}}$
$2{{x}^{2}}-2x+4 < {{x}^{2}}+2x+1$
${{x}^{2}}-4x+3 < 0$
$(x-1)(x-3) < 0$
$x=1$ atau $x=3$
$1 < x < 3$maka $a=1$ dan $b=3$
Maka: $a+2b=1+2.3=7$
Kunci: D
SBMPTN 2018 Matematika IPA Kode 402 No. 15
Diketahui dua lingkaran $x^2+y^2=2$ dan $x^2+y^2=4$. Garis $l_1$ menyinggung lingkaran pertama di titik $(1,-1)$. Garis $l_2$ menyinggung lingkaran kedua dan tegak lurus dengan garis $l_1$. Titik potong garis $l_1$ dan $l_2$ adalah ...
A. ($1+\sqrt 2$, $\sqrt 2-1$)
B. ($1-\sqrt 2$, $\sqrt 2-1$)
C. ($1+\sqrt 2$, $\sqrt 2+1$)
D. ($1-\sqrt 2$, $\sqrt 2-2$)
E. ($1+\sqrt 2$, $\sqrt 2+2$)
Pembahasan:
${{l}_{1}}$ adalah persamaan garis singgung lingkaran $x^2+y^2=2$ di titik $(1,-1)$ maka:
${{l}_{1}}\equiv {{x}_{1}}.x+{{y}_{1}}.y={{r}^{2}}$
${{l}_{1}}\equiv x-y=2$
${{l}_{1}}\equiv y=x-2\Rightarrow {{m}_{1}}=1$
${{l}_{1}}\bot {{l}_{2}}\Rightarrow {{m}_{1}}.{{m}_{2}}=-1\Leftrightarrow {{m}_{2}}=-1$
${{l}_{2}}$ adalah persamaan garis singgung lingkaran $x^2+y^2=4$ dengan gradien $-1$
$y=mx\pm r\sqrt{{{m}^{2}}+1}$
$y=-x\pm 2\sqrt{2}$
${{l}_{2}}\equiv y=-x+2\sqrt{2}$ atau ${{l}_{2}}\equiv y=-x-2\sqrt{2}$
Titik potong garis ${{l}_{1}}\equiv y=x-2$ dan garis ${{l}_{2}}\equiv y=-x+2\sqrt{2}$ adalah:
$y=y$
$x-2=-x+2\sqrt{2}$
$2x=2+2\sqrt{2}\Leftrightarrow x=1+\sqrt{2}$
$y=x-2$
$y=1+\sqrt{2}-2\Leftrightarrow y=\sqrt{2}-1$
Titik potongnya adalah $\left( 1+\sqrt{2},\sqrt{2}-1 \right)$
Kunci: A
Pembahasan:
${{l}_{1}}$ adalah persamaan garis singgung lingkaran $x^2+y^2=2$ di titik $(1,-1)$ maka:
${{l}_{1}}\equiv {{x}_{1}}.x+{{y}_{1}}.y={{r}^{2}}$
${{l}_{1}}\equiv x-y=2$
${{l}_{1}}\equiv y=x-2\Rightarrow {{m}_{1}}=1$
${{l}_{1}}\bot {{l}_{2}}\Rightarrow {{m}_{1}}.{{m}_{2}}=-1\Leftrightarrow {{m}_{2}}=-1$
${{l}_{2}}$ adalah persamaan garis singgung lingkaran $x^2+y^2=4$ dengan gradien $-1$
$y=mx\pm r\sqrt{{{m}^{2}}+1}$
$y=-x\pm 2\sqrt{2}$
${{l}_{2}}\equiv y=-x+2\sqrt{2}$ atau ${{l}_{2}}\equiv y=-x-2\sqrt{2}$
Titik potong garis ${{l}_{1}}\equiv y=x-2$ dan garis ${{l}_{2}}\equiv y=-x+2\sqrt{2}$ adalah:
$y=y$
$x-2=-x+2\sqrt{2}$
$2x=2+2\sqrt{2}\Leftrightarrow x=1+\sqrt{2}$
$y=x-2$
$y=1+\sqrt{2}-2\Leftrightarrow y=\sqrt{2}-1$
Titik potongnya adalah $\left( 1+\sqrt{2},\sqrt{2}-1 \right)$
Kunci: A
Artikel Terkait:
|
Semoga postingan: Soal dan Pembahasan Matematika IPA SBMPTN 2018 Kode 402 ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.
Post a Comment for "Soal dan Pembahasan Matematika IPA SBMPTN 2018 Kode 402"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.