Pembahasan Soal UTUL UGM 2014 Matematika IPA Kode 532

Berikut ini adalah Soal dan Pembahasan Matematika IPA UM-UGM 2014 Kode 532. Saya berharap kiranya pembahasan ini kiranya berguna bagi adik-adik yang berkeingin melanjutkan pendidikan tinggi ke salah satu PTN (Perguruan Tinggi Negeri) yang terletak di Daerah Istimewa Yogyakarta yaitu Universitas Gadjah Mada (UGM). Agar adik-adik dapat diterima sebagai mahasiswa/i baru di UGM maka perlu mempersiapkan diri dengan melatih diri menjawab soal-soal ujian tulis (UTUL) UGM tahun-tahun sebelumnya. Mari kita belajar dan berdiskusi melalui kolom komentar yang ada.

Matematika IPA UM-UGM 2014 No. 1

Tiga pria dan empat wanita akan duduk dalam satu baris. Banyak cara mereka duduk sehingga yang berjenis kelamin sama tidak berdampingan adalah ...
A. 24
B. 49
C. 144
D. 288
E. 5040
Pembahasan:
L = pria
P = wanita

= 4! × 3!
= 24 × 6
= 144
Kunci: C

Matematika IPA UM-UGM 2014 No. 2

Untuk setiap bilangan asli $n$ didefinisikan ${{A}_{n}}=\left( \begin{matrix} n & 2n \\ 3n & 4n \\ \end{matrix} \right)$. Jika $det(A_1+A_2+...+A_k)$ = -4050, maka $det(A_{2k})$ = ...
A. -800
B. -648
C. -512
D. -392
E. -288
Pembahasan:
${{A}_{1}}+{{A}_{2}}+{{A}_{3}}+...+{{A}_{k}}$ = $\left( \begin{matrix} 1+2+...+k & 2(1+2+...+k) \\ 3(1+2+...+k) & 4(1+2+...+k) \\ \end{matrix} \right)$
$\det \left( {{A}_{1}}+{{A}_{2}}+{{A}_{3}}+...+{{A}_{k}} \right)$ = $\left( \begin{matrix}
1+2+...+k & 2(1+2+...+k) \\ 3(1+2+...+k) & 4(1+2+...+k) \\ \end{matrix} \right)$
$-4050$ = $4{{(1+2+...+k)}^{2}}-6{{(1+2+...+k)}^{2}}$
$-4050$ = $-2{{(1+2+...+k)}^{2}}$
$2025$ = ${{\left( 1+2+...+k \right)}^{2}}$
$2025$ = ${{\left[ \frac{k(k+1)}{2} \right]}^{2}}$
$45$ = $\frac{k(k+1)}{2}$
$90=k(k+1)\Rightarrow k=9$
$\det {{A}_{2k}}=-2{{(-2k)}^{2}}$
$\det {{A}_{2k}}=-8{{k}^{2}}=-8.81=-648$
Kunci: B

Matematika IPA UM-UGM 2014 No. 3

Diketahui persamaan $x^2+px+q=0$ mempunyai akar-akar positif $x_1$ dan $x_2$. Jika $x_1$, 6, $x_2$ adalah tiga suku pertama barisan geometri dan $x_1$, $x_2$, 14 tiga suku pertama barisan aritmetika, maka $p+q$ = ...
A. 23
B. 24
C. 25
D. 26
E. 27
Pembahasan:
$x^2+px+q=0$, $x_1+x_2=-p$, $x_1.x_2=q$
Barisan Geometri: $x_1$, 6, $x_2$, maka:
$36={{x}_{1}}.{{x}_{2}}\Leftrightarrow 36=q$
$\frac{36}{{{x}_{2}}}={{x}_{1}}$
Barisan Aritmetika: $x_1$, $x_2$, 14, maka:
$2{{x}_{2}}={{x}_{1}}+14$
$2{{x}_{2}}=\frac{36}{{{x}_{2}}}+14$, kali dengan ${{x}_{2}}$
$2x_{2}^{2}-14x-36=0$
$x_{2}^{2}-7x-18=0$
$({{x}_{2}}-9)({{x}_{2}}+2)=0$
${{x}_{2}}=9$
$\frac{36}{{{x}_{2}}}={{x}_{1}}\Leftrightarrow \frac{36}{9}={{x}_{1}}=4$
${{x}_{1}}+{{x}_{2}}=-p\Leftrightarrow 9+4=-p\Leftrightarrow -13=p$
$p+q=-13+36=23$
Kunci: A

Matematika IPA UM-UGM 2014 No. 4

Jika $f(x)=(\sin x + \cos x)(\cos 2x + \sin 2x)$ dan $f'(x)=2\cos 3x + g(x)$ maka $g(x)$ = ...
A. $\cos 3x + \sin x$
B. $\cos 3x - \sin x$
C. $\cos x + \sin x$
D. $\cos x - \sin x$
E. $-\cos x + \sin x$
Pembahasan:
$f(x)=(\sin x + \cos x)(\cos 2x + \sin 2x)$
$=\sin x\cos 2x+\sin x\sin 2x$
$+\cos x\cos 2x+\cos x\sin 2x$
$=\sin x\cos 2x+\cos x\sin 2x$
$\cos 2x\cos x+\sin 2x\sin x$
$f(x)=\sin 3x+\cos x$
$f'(x)=3\cos 3x-\sin x$; $f'(x)=2\cos 3x + g(x)$
$2co3x+g(x)=3\cos 3x-\sin x$
$g(x)=\cos 3x-\sin x$
Kunci: B

Matematika IPA UM-UGM 2014 No. 5

Diketahui $D_1$ adalah daerah di kuadran I yang dibatasi oleh parabola $y=\frac{9}{4}x^2$, parabola $y=x^2$, dan garis $x=2$, dan ${{D}_{2}}$ daerah yang dibatasi oleh garis $x=2$, garis $y=9$, parabola $y={{x}^{2}}$. Jika luas $D_1=a$, maka luas $D_2$ adalah ...
A. $\frac{7}{10}a$
B. $\frac{8}{10}a$
C. $\frac{9}{10}a$
D. $\frac{11}{10}a$
E. $\frac{13}{10}a$
Pembahasan:
Perhatikan gambar berikut ini!

$L.{{D}_{1}}=\frac{1}{3}.alas.({{t}_{2}}-{{t}_{1}})$
$L.{{D}_{1}}=\frac{1}{3}.2.(9-4)$
$L.{{D}_{1}}=\frac{10}{3}=a$
$L.{{D}_{2}}=\int\limits_{2}^{3}{(9-{{x}^{2}})dx}$
$L.{{D}_{2}}=\left. 9x-\frac{1}{3}{{x}^{3}} \right]_{2}^{3}=\frac{8}{3}$
$\frac{L.{{D}_{2}}}{L.{{D}_{1}}}=\frac{L.{{D}_{2}}}{a}$
$\frac{\frac{8}{3}}{\frac{10}{3}}=\frac{L.{{D}_{2}}}{a}$
$\frac{8}{10}a=L.{{D}_{2}}$
Kunci: B

Matematika IPA UM-UGM 2014 No. 6

Diketahui matriks A berukuran 3 x 3 dan memenuhi: $A\left( \begin{matrix} 1 \\ 2 \\ 1 \\ \end{matrix} \right)=\left( \begin{matrix} 2 \\ 2 \\ 2 \\ \end{matrix} \right)$ dan $A\left( \begin{matrix} 1 \\ 2 \\ 3 \\ \end{matrix} \right)=\left( \begin{matrix} 2 \\ 4 \\ 2 \\ \end{matrix} \right)$. Jika $x=\left( \begin{matrix} 2 \\ 4 \\ 10 \\ \end{matrix} \right)$ maka $Ax$ = …
A. $\left( \begin{matrix} 8 \\ 4 \\ 8 \\ \end{matrix} \right)$
B. $\left( \begin{matrix} 4 \\ 12 \\ 4 \\ \end{matrix} \right)$
C. $\left( \begin{matrix} 12 \\ 8 \\ 12 \\ \end{matrix} \right)$
D. $\left( \begin{matrix} 4 \\ 8 \\ 4 \\ \end{matrix} \right)$
E. $\left( \begin{matrix} 8 \\ 12 \\ 8 \\ \end{matrix} \right)$
Pembahasan:
Misalkan matriks $A=\left( \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right)$, maka:
$\left( \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right)\left( \begin{matrix} 1 \\ 2 \\ 1 \\ \end{matrix} \right)=\left( \begin{matrix} 2 \\ 2 \\ 2 \\ \end{matrix} \right)$
$a+2b+c=2$ … persamaan (1)
$d+2e+f=2$ …persamaan (2)
$g+2h+i=2$ … persamaan (3)
$\left( \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right)\left( \begin{matrix} 1 \\ 2 \\ 3 \\ \end{matrix} \right)=\left( \begin{matrix} 2 \\ 4 \\ 2 \\ \end{matrix} \right)$
$a+2b+3c=2$ … persamaan (4)
$d+2e+3f=4$… persamaan (5)
$g+2h+3i=2$ … persamaan (6)
Dari (1) dan (4) diperoleh: c = 0, dan $a+2b=2$
Dari (2) dan (5) diperoleh: f = 1, dan $d+2e=1$
Dari (3) dan (6) diperoleh: I = 0, dan $g+2h=2$
$Ax=\left( \begin{matrix} a & b & 0 \\ d & e & 1 \\ g & h & 0 \\ \end{matrix} \right)\left( \begin{matrix} 2 \\ 4 \\ 10 \\ \end{matrix} \right)$
$=\left( \begin{matrix} 2a+4b \\ 2d+4e+10 \\ 2g+4h \\ \end{matrix} \right)$
$=\left( \begin{matrix} 2(a+2b) \\ 2(d+2e)+10 \\ 2(g+2h) \\ \end{matrix} \right)$
$=\left( \begin{matrix} 2.2 \\ 2.1+10 \\ 2.2 \\ \end{matrix} \right)=\left( \begin{matrix} 4 \\ 12 \\ 4 \\ \end{matrix} \right)$
Kunci: B

Matematika IPA UM-UGM 2014 No. 7

Diberikan segitiga ABC dengan $\angle A=\alpha $, $\angle B={{90}^{o}}$, dan $\angle C=\gamma $. Jika $\cos \alpha = x$, maka $\cos (\alpha +2\gamma )$ = …
A. $-x$
B. $-\sqrt{1-{{x}^{2}}}$
C. $x$
D. $\sqrt{1-{{x}^{2}}}$
E. 1
Pembahasan:
Perhatikan gambar berikut!

$\alpha +\gamma ={{90}^{o}}$
$\cos (\alpha +2\gamma )=\cos (\alpha +\gamma +\gamma )$
$=\cos ({{90}^{o}}+\gamma )$
$=-\sin \gamma $
$=-x$
Kunci: A

Matematika IPA UM-UGM 2014 No. 8

Jika garis $y=mx+k$ menyinggung lingkaran ${{x}^{2}}+{{y}^{2}}-10x+6y+24=0$ di titik $(8,-4)$ maka nilai $(m+k)$ adalah …
A. -26
B. -25
C. -24
D. -23
E. -22
Pembahasan:
Persamaan garis singgung ${{x}^{2}}+{{y}^{2}}-10x+6y+24=0$ di titik $(8,-4)$ adalah:
${{x}_{1}}.x+{{y}_{1}}.y-\frac{10}{2}(x+{{x}_{1}})+\frac{6}{2}(y+{{y}_{1}})+24=0$
$8x-4y-5(x+8)+3(y-4)+24=0$
$3x-y-28=0$
$y=3x-28$
$y=mx+k$
$m=3,k=-28\Rightarrow m+k=-25$
Kunci: B

Matematika IPA UM-UGM 2014 No. 9

Sebuah prisma ABCD.EFGH memiliki alas berbentuk persegi. Titik T adalah titik tengah diagonal HF. Jika $\angle EAT=\frac{\pi }{6}$ dan volume prisma tersebut $4\sqrt{6}$, maka tinggi prisma adalah …
A. $\sqrt{6}$
B. $\sqrt{3}$
C. $\sqrt{2}$
D. $\frac{\sqrt{3}}{2}$
E. $\frac{\sqrt{2}}{2}$
Pembahasan:

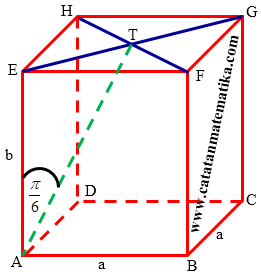
Perhatikan segitiga AET siku-siku di E, maka:
$\tan A=\frac{ET}{EA}$
$\tan \frac{\pi }{6}=\frac{\frac{1}{2}a\sqrt{2}}{b}$
$\frac{1}{\sqrt{3}}=\frac{\frac{1}{2}a\sqrt{2}}{b}$
$b=\frac{a}{2}\sqrt{6}$
Volume prisma = $4\sqrt{6}$
$V={{a}^{2}}b$
$4\sqrt{6}={{a}^{2}}.\frac{a}{2}\sqrt{6}$
$8={{a}^{3}}\Leftrightarrow a=2$
Tinggi prisma = $b=\frac{a}{2}\sqrt{6}=\sqrt{6}$
Kunci: A

Matematika IPA UM-UGM 2014 No. 10

Diketahui vektor $\vec{a}$ dan $\vec{b}$ membentuk sudut sebesar $\theta $. Jika panjang proyeksi vektor $\vec{b}$ pada $\vec{a}$ sama dengan $2\sin \theta $ dan panjang vektor $\vec{b}$ adalah 1, maka $\tan 2\theta $ = …
A. $\frac{1}{3}$
B. $\frac{2}{3}$
C. 1
D. $\frac{4}{3}$
E. $\frac{5}{3}$
Pembahasan:
$\angle (\vec{a},\vec{b})=\theta $, $|\vec{b}|=1$
$\frac{\vec{b}.\vec{a}}{|\vec{a}|}=2\sin \theta $
$\frac{|\vec{b}|.|\vec{a}|.cos\theta }{|\vec{a}|}=2\sin \theta $
$\cos \theta =2\sin \theta $
$\tan \theta =\frac{1}{2}$
$\tan 2\theta =\frac{2\tan \theta }{1-{{\tan }^{2}}\theta }$
$\tan 2\theta =\frac{2.\frac{1}{2}}{1-\frac{1}{4}}=\frac{1}{\frac{3}{4}}=\frac{4}{3}$
Kunci: D

Matematika IPA UM-UGM 2014 No. 11

Semua nilai $a$ agar $\sqrt{2{{x}^{2}}-x+14}\ge \sqrt{{{x}^{2}}-ax+10}$ benar untuk semua bilangan real $x$ adalah …
A. $|a|\le 6$
B. $a\le -3$ atau $a\ge 5$
C. $a\le -5$ atau $a\ge 3$
D. $-3\le a\le 5$
E. $-6\le a\le -5$ atau $3\le a\le 6$
Pembahasan:
(*) $\sqrt{2{{x}^{2}}-x+14}\ge \sqrt{{{x}^{2}}-ax+10}$
$2{{x}^{2}}-x+14\ge {{x}^{2}}-ax+10$
${{x}^{2}}+(a-1)x+4\ge 0$, definit positif, maka:
$D\le 0$
${{B}^{2}}-4AC\le 0$
${{(a-1)}^{2}}-4.1.4\le 0$
${{a}^{2}}-2a-15\le 0$
$(a+3)(a-5)\le 0$
$-3\le a\le 5$
(**) syarat:
$2{{x}^{2}}-x+14\ge 0$
${{x}^{2}}-ax+10\ge 0$
$D\le 0$
${{B}^{2}}-4AC\le 0$
${{a}^{2}}-4.1.10\le 0$
$(a+\sqrt{40})(a-\sqrt{40})\le 0$
$-\sqrt{40}\le a\le \sqrt{40}$
Dari (*) dan (**) diperoleh penyelesaian $-3\le a\le 5$
Kunci: D

Matematika IPA UM-UGM 2014 No. 12

Jika $P(x)={{x}^{5}}+a{{x}^{4}}+{{x}^{2}}+bx+2$ dibagi $h(x)={{x}^{3}}+2{{x}^{2}}-x-2$ memberikan sisa $r(x)={{x}^{2}}-3x+4$ maka $a+b$ = …
A. -2
B. -1
C. 1
D. 2
E. 3
Pembahasan:
Yang dibagi = pembagi x hasil + Sisa
$P(x)=h(x).hasil+r(x)$
${{x}^{5}}+a{{x}^{4}}+{{x}^{2}}+bx+2$$=({{x}^{3}}+2{{x}^{2}}-x-2).hasil+{{x}^{2}}-3x+4$
${{x}^{5}}+a{{x}^{4}}+{{x}^{2}}+bx+2$$=(x-1)(x+1)(x-2).hasil+{{x}^{2}}-3x+4$
x=1, maka:
$1+a+1+b+2=1-3+4$
$a+b=2$
Kunci: D

Matematika IPA UM-UGM 2014 No. 13

Jika $a$ memenuhi persamaan ${}^{2}\log 2x+{}^{3}\log 3x={}^{4}\log 4{{x}^{2}}$, maka ${}^{a}\log 3$ = …
A. -3
B. -2
C. -1
D. 1
E. 2
Pembahasan:
${}^{2}\log 2+{}^{2}\log x+{}^{3}\log 3+{}^{3}\log x$$={}^{4}\log 4+{}^{4}\log {{x}^{2}}$
$1+{}^{2}\log x+1+{}^{3}\log x=1+{}^{{{2}^{2}}}\log {{x}^{2}}$
$1+{}^{2}\log x+1+{}^{3}\log x=1+{}^{{{2}^{2}}}\log {{x}^{2}}$
${}^{3}\log x=-1$
$x={{3}^{-1}}=a$
${}^{a}\log 3={}^{{{3}^{-1}}}\log 3=-1$
Kunci: C

Matematika IPA UM-UGM 2014 No. 14

Diketahui $f(x)=\sqrt{1+x}$. Nilai $\underset{h\to 0}{\mathop{\lim }}\,\frac{f(3+2{{h}^{2}})-f(3-3{{h}^{2}})}{{{h}^{2}}}$ adalah …
A. 0
B. $\frac{2}{3}$
C. $\frac{6}{7}$
D. $\frac{9}{8}$
E. $\frac{5}{4}$
Pembahasan:
$\underset{h\to 0}{\mathop{\lim }}\,\frac{f(3+2{{h}^{2}})-f(3-3{{h}^{2}})}{{{h}^{2}}}$
$=\underset{h\to 0}{\mathop{\lim }}\,\frac{\sqrt{1+3+2{{h}^{2}}}-\sqrt{1+3-3{{h}^{2}}}}{{{h}^{2}}}$
$=\underset{h\to 0}{\mathop{\lim }}\,\frac{\sqrt{4+2{{h}^{2}}}-\sqrt{4-3{{h}^{2}}}}{{{h}^{2}}}\times \frac{\sqrt{4+2{{h}^{2}}}+\sqrt{4-3{{h}^{2}}}}{\sqrt{4+2{{h}^{2}}}+\sqrt{4-3{{h}^{2}}}}$
$=\underset{h\to 0}{\mathop{\lim }}\,\frac{4+2{{h}^{2}}-(4-3{{h}^{2}})}{{{h}^{2}}\sqrt{4+2{{h}^{2}}}+\sqrt{4-3{{h}^{2}}}}$
$=\underset{h\to 0}{\mathop{\lim }}\,\frac{5{{h}^{2}}}{{{h}^{2}}\sqrt{4+2{{h}^{2}}}+\sqrt{4-3{{h}^{2}}}}$
$=\underset{h\to 0}{\mathop{\lim }}\,\frac{5}{\sqrt{4+2{{h}^{2}}}+\sqrt{4-3{{h}^{2}}}}$
$=\frac{5}{\sqrt{4+{{2.0}^{2}}}+\sqrt{4-{{3.0}^{2}}}}$
$=\frac{5}{4}$
Kunci: E

Matematika IPA UM-UGM 2014 No. 15

Diketahui jumlah empat suku pertama suatu barisan aritmetika sama dengan jumlah tiga suku selanjutnya. Jika jumlah 10 suku pertama adalah 270, maka suku pertama barisan tersebut adalah …
A. 2
B. 3
C. 6
D. 9
E. 18
Pembahasan:
Barisan Arimetika:
${{S}_{4}}={{U}_{5}}+{{U}_{6}}+{{U}_{7}}$
$\frac{4}{2}(2a+3b)=a+4b+a+5b+a+6b$
$4a+6b=3a+15b$
$a=9b$
${{S}_{10}}=270$
$\frac{10}{2}(2a+9b)=270$
$2a+9b=54$
$2.9b+9b=54$
$27b=54$
$b=2$
$a=9b\Leftrightarrow a=9.2=18$
Kunci: E

Semoga postingan: Pembahasan Soal UTUL UGM 2014 Matematika IPA Kode 532 ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :