Pembahasan Soal SIMAK UI 2018 Matematika IPA Kode 416
Berikut ini adalah Soal dan Pembahasan Matematika IPA SIMAK UI 2018 dengan Kode Soal 416. Soal ini merupakan salah satu alat tes untuk menyeleksi mahasiswa/i tahun ajaran 2018/2019 yang akan mengecap pendidikan tinggi di universitas ternama di Indonesia yaitu Universitas Indonesia (UI). Universitas Indonesia terletak di Jl. Margonda Raya, Beji, Pondok Cina Kota Depok Jawa Barat. Pembahasan SIMAK UI 2018/2019 ini adalah hasil pemikiran sederhana saya yang tentu masih jauh dari kata sempurna. Saya sangat menghargai kritik dan saran dari pengunjung setia Catatan Matematika yang sifatnya membangun dan mari diskusi dan belajar bersama melalui kolom komentar di akhir postingan ini.
A. 12
B. 10
C. 9
D. 8
E. 5
Suku banyak $f(x)$ dibagi $x^2+x-2$ bersisa $ax+b$, maka:
$f(x)$ = ($x^2+x-2$)Hasil + $ax+b$
$f(x)$ = $(x+2)(x-1)$Hasil + $ax+b$
$f(-2)$ = $(-2+2)(-2-1)$Hasil + $-2a+b$
$f(-2)$ = $-2a+b=7$ … persamaan (1)
$f(1)$ = $(1+2)(1-1)$Hasil + $a+b$
$f(1)$ = $a+b$ … persamaan (2)
Suku banyak $f(x)$ dibagi $x^2-4x+3$ bersisa $2bx+a-1$, maka:
$f(x)$ = ($x^2-4x+3$)Hasil + $2bx+a-1$
$f(x)$ = $(x-1)(x-3)$Hasil + $2bx+a-1$
$f(1)$ = $(1-1)(1-3)$Hasil + $2b+a-1$
$f(1)$ = $2b+a-1$ substitusi ke persamaan (2), maka:
$2b+a-1=a+b$
$b=1$
Substitusi ke persamaan (1), maka:
$-2a+b=7\Leftrightarrow -2a+1=7\Leftrightarrow a=-3$
${{a}^{2}}+{{b}^{2}}={{(-3)}^{2}}+{{1}^{2}}=10$
Jawaban: B
A. {$x\in R:-4\le x\le 4$}
B. {$x\in R:-4\le x\le 3$}
C. {$x\in R:x\le -4$ atau $x\ge 4$}
D. {$x\in R:0\le x\le 3$}
E. {$x\in R:x\le -4$ atau $x\ge 3$}
$16-x^2\le |x+4|$
$16-x^2\le x+4$
$12-x^2-x\le 0$
$x^2+x-12\ge 0$
$(x+4)(x-3)\ge 0$
$x\le -4$ atau $x\ge 3$
yang memenuhi syarat $x\ge -4$ adalah $x\ge 3$.
(ii) Untuk $x\le 4$, maka:
$16-x^2\le |x+4|$
$16-x^2\le -(x+4)$
$20-x^2+x\le 0$
$x^2-x-20\ge 0$
$(x-5)(x+4)\ge 0$
$x\le -4$ atau $x\ge 5$
yang memenuhi syarat $x\le 4$ adalah $x\le -4$
Dari i) dan (ii) diperoleh:
{$x\in R:x\le -4$ atau $x\ge 3$}
Jawaban: E
A. $\frac{\pi }{3}$
B. $\frac{2\pi }{3}$
C. $\pi $
D. $\frac{4}{3}\pi $
E. $2\pi $
$2(1-{{\cos }^{2}}x)-\cos x=1$
$2{{\cos }^{2}}x+\cos x-1=0$
$(2\cos x-1)(\cos x+1)=0$
$\cos x=\frac{1}{2}\Rightarrow {{x}_{1}}={{60}^{o}}$ atau
$\cos x=-1\Leftrightarrow {{x}_{2}}={{180}^{o}}$
${{x}_{1}}+{{x}_{2}}={{60}^{o}}+{{180}^{o}}$
${{x}_{1}}+{{x}_{2}}={{240}^{o}}=\frac{{{240}^{o}}}{{{180}^{o}}}\pi =\frac{4}{3}\pi $
Jawaban: D
A. -4
B. -2
C. 0
D. 2
E. 4
$\underset{x\to -3}{\mathop{\lim }}\,\frac{3+ax}{3ax(b{{x}^{3}}+27)}=-\frac{1}{{{3}^{5}}}$
Untuk $x=-3$ maka:
$3+ax=0\Leftrightarrow 3-3a=0\Leftrightarrow a=1$
Untuk $x=-3$ maka:
$b{{x}^{3}}+27=0\Leftrightarrow b.{{(-3)}^{3}}+27=0\Leftrightarrow b=1$
$a+b=1+1=2$
Jawaban: E
A. 5
B. 10
C. 15
D. 18
E. 27
$\int\limits_{y=1}^{y=9}{f(3y+3)dy}$
$x=3y+3$ maka $\frac{dx}{dy}=3\Leftrightarrow dy=\frac{1}{3}dx$
$y=1\Rightarrow x=6$
$y=9\Rightarrow x=30$
$\int\limits_{1}^{9}{f(3y+3)dy}=\int\limits_{6}^{30}{f(x).\frac{1}{3}dx}$
$=\frac{1}{3}\int\limits_{6}^{30}{f(x)dx}$
$=\frac{1}{3}.30=10$
Jawaban: B
A. $\frac{\sqrt{35}}{36}$
B. $\frac{\sqrt{37}}{36}$
C. $\frac{\sqrt{38}}{36}$
D. $\frac{\sqrt{39}}{36}$
E. $\frac{\sqrt{41}}{36}$

Bidang $\alpha$ adalah bidang MNN’O (berupa persegipanjang)
Perhatikan segitiga MM’N siku-siku di titik M, dengan MM’ = 6 cm, M’N = 1 cm, maka:
$MN=\sqrt{{{6}^{2}}+{{1}^{1}}}=\sqrt{37}$
Luas bidang $\alpha$ adalah:
$=N'N\times MN$
$=2\sqrt{37}$
Luas permukaan balok adalah:
$=2(p.l+p.t+l.t)$
$=2(6.3+6.2+3.2)=72$
$\frac{\alpha }{L.balok}=\frac{2\sqrt{37}}{72}=\frac{\sqrt{37}}{36}$
Jawaban: B
A. $-\frac{7\sqrt{11}}{33}$
B. $-\frac{7\sqrt{11}}{44}$
C. $\frac{7\sqrt{11}}{33}$
D. $\frac{7\sqrt{11}}{44}$
E. $\frac{7\sqrt{11}}{55}$

Sudut terbesar antara rusuk CG dan bidang PBD adalah $\alpha $, dengan $\alpha ={{180}^{o}}-\angle CPQ$
$CQ=7\sqrt{2}$, CP = 10, maka:
$PQ=\sqrt{C{{Q}^{2}}+C{{P}^{2}}}$
$PQ=\sqrt{{{(7\sqrt{2})}^{2}}+{{10}^{2}}}$
$PQ=3\sqrt{22}$
$\sin \alpha =\sin ({{180}^{o}}-\angle CPQ)$
$\sin \alpha =\sin \angle CPQ$
$\sin \alpha =\frac{CQ}{PQ}$
$\sin \alpha =\frac{7\sqrt{2}}{3\sqrt{22}}$
$\sin \alpha =\frac{7}{3\sqrt{11}}\times \frac{\sqrt{11}}{\sqrt{11}}=\frac{7\sqrt{11}}{33}$
Jawaban: C
A. 72
B. 80
C. 81
D. 86
E. 88
Misal: ${{3}^{x}}=a$ dan ${{3}^{y}}=b$ , maka
$a+b=18\Leftrightarrow a=18-b$ nilai maksimum $ab=...?$
$L=a.b$
$L=a(18-a)$
$L=18a-{{a}^{2}}$
Maksimum/minimum, maka $L'=0$
$18-2a=0\Leftrightarrow a=9$
$L=18a-{{a}^{2}}\Leftrightarrow L=18.9-{{9}^{2}}=81$
Jawaban: C
A. $\frac{1}{6}$
B. $\frac{4}{3}$
C. 3
D. 4
E. 6

Dari gambar diperoleh:
Lingkaran melalui berpusat di titik (-2,-1) dan berjari-jari 1, maka persamaan lingkarannya adalah:
${{(x+2)}^{2}}+{{(y+1)}^{2}}={{1}^{2}}$, $y=sx$
${{(x+2)}^{2}}+{{(sx+1)}^{2}}=1$
$x^2+4x+4+{{s}^{2}}x^2+2sx+1=1$
$({{s}^{2}}+1)x^2+(2s+4)x+4=0$, syarat menyinggung $D=0$,
${{b}^{2}}-4ac=0$
${{(2s+4)}^{2}}-4({{s}^{2}}+1)4=0$
$4{{s}^{2}}+16s+16-16{{s}^{2}}-16=0$
$-12{{s}^{2}}+16s=0$
$-4s(3s-4)=0$
$-4s=0$ atau $3s=4$
Jawaban: D
A. 6
B. 7
C. 8
D. 9
E. 10
$A=a-2$, $B=\sqrt{3}(1-a)$, $C=a-2$,
Selalu berada di atas sumbu-X (definit positif), maka:
(1) $A > 0\Leftrightarrow a-2 > 0\Leftrightarrow a>2$
(2) $D < 0$
$B^2-4AC < 0$
${{[\sqrt{3}(1-a)]}^{2}}-4(a-2)(a-2) < 0$
$3(1-2a+{{a}^{2}})-4({{a}^{2}}-4a+4) < 0$
$3-6a+3{{a}^{2}}-4{{a}^{2}}+16a-16 < 0$
$-{{a}^{2}}+10a-13 < 0$
${{a}^{2}}-10a+13 > 0$, dengan rumus abc maka:
$a=\frac{10\pm \sqrt{48}}{2}$
$a=\frac{10\pm 4\sqrt{3}}{2}$
$a=5\pm 2\sqrt{3}$
$a < 5-2\sqrt{3}$ atau $a > 5+2\sqrt{3}$
Dari (1) dan (2) diperoleh batas nilai $a$ adalah:
$a > 5+2\sqrt{3}\Leftrightarrow a > 5+\sqrt{12}$
$a-2 > 5+\sqrt{12}-2$, karena diminta bilangan bulat terkecil, maka:
$a-2=5+\sqrt{16}-2=7$
Jawaban: B
A. 0
B. 1
C. 2
D. 3
E. 6
$a+b=2+c$
${{(a+b)}^{2}}={{(2+c)}^{2}}$
${{a}^{2}}+{{b}^{2}}+2ab={{c}^{2}}+4c+4$
${{a}^{2}}+{{b}^{2}}-4{{c}^{2}}=2$
-----------------------------------(-)
$2ab+4{{c}^{2}}={{c}^{2}}+4c+2$
$3{{c}^{2}}-4c+2ab-2=0$, diketahui $ab=\frac{3}{2}{{c}^{2}}$
$3{{c}^{2}}-4c+2.\frac{3}{2}{{c}^{2}}-2=0$
$6{{c}^{2}}-4c-2=0$
$3{{c}^{2}}-2c-1=0$
$(3c+1)(c-1)=0$
$c=-\frac{1}{3}$ atau $c=1$
Jawaban: B
A. 3
B. 16
C. 32
D. 64
E. 254
(1) $\vec{u}+k\vec{v}$ tegak lurus $\vec{u}$ bila $k=\frac{17}{18}$
(2) sudut antara $\vec{u}$ dan $\vec{v}$ adalah sudut tumpul.
(3) $||pro{{y}_{{\vec{u}}}}\vec{v}||=6$
(4) Jarak antara $\vec{u}$ dan $\vec{v}$ sama dengan $||\vec{u}+\vec{v}||$
$\vec{u}+k\vec{v}$ tegak lurus $\vec{u}$, maka:
$(\vec{u}+k\vec{v}).\vec{u}=0$
$\left( \begin{matrix} 2+4k \\ -1+10k \\ 2-8k \\ \end{matrix} \right).\left( \begin{matrix} 2 \\ -1 \\ 2 \\ \end{matrix} \right)=0$
$4+4k+1-10k+4-16k=0$
$-22k=-9\Leftrightarrow k=\frac{9}{22}$,
Pernyataan (1) SALAH
Pernyataan (2)
$\cos (u,v)=\frac{u.v}{|u||v|}$
$\cos (u,v)=\frac{\left( \begin{matrix} 2 \\ -1 \\ 2 \\ \end{matrix} \right).\left( \begin{matrix} 4 \\ 10 \\ -8 \\ \end{matrix} \right)}{\sqrt{4+1+4}.\sqrt{16+100+64}}$
$\cos (u,v)=\frac{8-10-16}{3.6\sqrt{5}}$
$\cos (u,v)=\frac{-18}{18\sqrt{5}}$, karena nilainya negatif maka sudut antara $\vec{u}$ dan $\vec{v}$ adalah sudut tumpul. Pernyataan (2) BENAR.
Berdasarkan petunjuk C, tanpa mengecek pernyataan (4) maka opsi yang memenuhi adalah C.
Jawaban: C
(1) nilai minimum lokal $y=b-\frac{2}{3}{{a}^{\frac{3}{2}}}$
(2) nilai maksimum lokal $y=b+\frac{2}{3}{{a}^{\frac{3}{2}}}$
(3) $y$ stasioner saat $x={{a}^{\frac{1}{2}}}$
(4) naik pada interval $\left[ -\infty ,-{{a}^{\frac{1}{2}}} \right]$
$\frac{dy}{dx}=x^2-a=0$, karena $a > 0$ maka:
$(x+\sqrt{a})(x-\sqrt{a})=0$
$x=-\sqrt{a}$ atau $x=\sqrt{a}$,
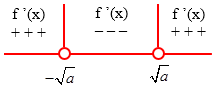
Dari gambar garis bilangan, maka: pernyataan (3) dan (4) BENAR.
$y=\frac{1}{3}{{x}^{3}}-ax+b$
$x=-\sqrt{a}\Rightarrow y=b+\frac{2}{3}{{a}^{\frac{3}{2}}}$ (nilai maksimum lokal), pernyataan (1) BENAR.
$x=\sqrt{a}\Rightarrow y=b-\frac{2}{3}{{a}^{\frac{3}{2}}}$ (nilai minimum lokal), pernyataan (2) BENAR.
Jawaban: E
(1) ${{\sin }^{4}}\alpha +{{\cos }^{4}}\alpha =\frac{6}{8}$
(2) ${{\sin }^{6}}\alpha +{{\cos }^{6}}\alpha =\frac{12}{16}$
(3) ${{\cos }^{4}}\alpha =\frac{1}{2}-\frac{1}{4}\sqrt{3}$
(4) ${{\sin }^{4}}\alpha =\frac{7}{16}-\frac{1}{4}\sqrt{3}$
$\sin {{15}^{o}}=\sin ({{45}^{o}}-{{30}^{o}})$
$\sin {{15}^{o}}=\sin {{45}^{o}}\cos {{30}^{o}}-\cos {{45}^{o}}\sin {{30}^{o}}$
$\sin {{15}^{o}}=\frac{1}{2}\sqrt{2}.\frac{1}{2}\sqrt{3}-\frac{1}{2}\sqrt{2}.\frac{1}{2}$
$\sin {{15}^{o}}=\frac{\sqrt{6}-\sqrt{2}}{4}$
${{\sin }^{2}}{{15}^{o}}={{\left( \frac{\sqrt{6}-\sqrt{2}}{4} \right)}^{2}}$
${{\sin }^{2}}{{15}^{o}}=\frac{2-\sqrt{3}}{4}$
${{\sin }^{4}}{{15}^{o}}={{\left( \frac{2-\sqrt{3}}{4} \right)}^{2}}=\frac{7}{16}-\frac{1}{4}\sqrt{3}$, pernyataan (4) BENAR.
Dengan cara yang sama:
$\cos {{15}^{o}}=\frac{\sqrt{6}+\sqrt{2}}{4}$
${{\cos }^{2}}{{15}^{o}}=\frac{2+\sqrt{3}}{4}$
${{\cos }^{4}}{{15}^{o}}={{\left( \frac{2+\sqrt{3}}{4} \right)}^{2}}=\frac{7}{16}-\frac{1}{4}\sqrt{3}$, pernyataan (3) SALAH.
Dengan logika, berdasarkan petunjuk C maka kita sudah dapat menentukan opsi yang memenuhi adalah D.
Jawaban: D
Soal SIMAK UI 2018 - Matematika IPA No. 1
Diketahui suku banyak $f(x)$ dibagi ${{x}^{2}}+x-2$ bersisa $ax+b$ dan dibagi ${{x}^{2}}-4x+3$ bersisa $2bx+a-1$. Jika $f(-2)=7$, maka ${{a}^{2}}+{{b}^{2}}$ = …A. 12
B. 10
C. 9
D. 8
E. 5
Penyelesaian: Lihat/Tutup
Yang dibagi = Pembagi x Hasil bagi + SisaSuku banyak $f(x)$ dibagi $x^2+x-2$ bersisa $ax+b$, maka:
$f(x)$ = ($x^2+x-2$)Hasil + $ax+b$
$f(x)$ = $(x+2)(x-1)$Hasil + $ax+b$
$f(-2)$ = $(-2+2)(-2-1)$Hasil + $-2a+b$
$f(-2)$ = $-2a+b=7$ … persamaan (1)
$f(1)$ = $(1+2)(1-1)$Hasil + $a+b$
$f(1)$ = $a+b$ … persamaan (2)
Suku banyak $f(x)$ dibagi $x^2-4x+3$ bersisa $2bx+a-1$, maka:
$f(x)$ = ($x^2-4x+3$)Hasil + $2bx+a-1$
$f(x)$ = $(x-1)(x-3)$Hasil + $2bx+a-1$
$f(1)$ = $(1-1)(1-3)$Hasil + $2b+a-1$
$f(1)$ = $2b+a-1$ substitusi ke persamaan (2), maka:
$2b+a-1=a+b$
$b=1$
Substitusi ke persamaan (1), maka:
$-2a+b=7\Leftrightarrow -2a+1=7\Leftrightarrow a=-3$
${{a}^{2}}+{{b}^{2}}={{(-3)}^{2}}+{{1}^{2}}=10$
Jawaban: B
Soal SIMAK UI 2018 - Matematika IPA No. 2
Himpunan penyelesaian $16-x^2\le |x+4|$ adalah …A. {$x\in R:-4\le x\le 4$}
B. {$x\in R:-4\le x\le 3$}
C. {$x\in R:x\le -4$ atau $x\ge 4$}
D. {$x\in R:0\le x\le 3$}
E. {$x\in R:x\le -4$ atau $x\ge 3$}
Penyelesaian: Lihat/Tutup
(i) Untuk $x\ge -4$ maka:$16-x^2\le |x+4|$
$16-x^2\le x+4$
$12-x^2-x\le 0$
$x^2+x-12\ge 0$
$(x+4)(x-3)\ge 0$
$x\le -4$ atau $x\ge 3$
yang memenuhi syarat $x\ge -4$ adalah $x\ge 3$.
(ii) Untuk $x\le 4$, maka:
$16-x^2\le |x+4|$
$16-x^2\le -(x+4)$
$20-x^2+x\le 0$
$x^2-x-20\ge 0$
$(x-5)(x+4)\ge 0$
$x\le -4$ atau $x\ge 5$
yang memenuhi syarat $x\le 4$ adalah $x\le -4$
Dari i) dan (ii) diperoleh:
{$x\in R:x\le -4$ atau $x\ge 3$}
Jawaban: E
Soal SIMAK UI 2018 - Matematika IPA No. 3
Jika ${{x}_{1}}$ atau ${{x}_{2}}$ memenuhi persamaan $2{{\sin }^{2}}x-\cos x=1$, $0\le x\le \pi $, nilai ${{x}_{1}}+{{x}_{2}}$ adalah …A. $\frac{\pi }{3}$
B. $\frac{2\pi }{3}$
C. $\pi $
D. $\frac{4}{3}\pi $
E. $2\pi $
Penyelesaian: Lihat/Tutup
$2{{\sin }^{2}}x-\cos x=1$$2(1-{{\cos }^{2}}x)-\cos x=1$
$2{{\cos }^{2}}x+\cos x-1=0$
$(2\cos x-1)(\cos x+1)=0$
$\cos x=\frac{1}{2}\Rightarrow {{x}_{1}}={{60}^{o}}$ atau
$\cos x=-1\Leftrightarrow {{x}_{2}}={{180}^{o}}$
${{x}_{1}}+{{x}_{2}}={{60}^{o}}+{{180}^{o}}$
${{x}_{1}}+{{x}_{2}}={{240}^{o}}=\frac{{{240}^{o}}}{{{180}^{o}}}\pi =\frac{4}{3}\pi $
Jawaban: D
Soal SIMAK UI 2018 - Matematika IPA No. 4
Jika $\underset{x\to -3}{\mathop{\lim }}\,\frac{\frac{1}{ax}+\frac{1}{3}}{b{{x}^{3}}+27}=-\frac{1}{{{3}^{5}}}$, nilai $a+b$ untuk $a$ dan $b$ bilangan bulat positif adalah …A. -4
B. -2
C. 0
D. 2
E. 4
Penyelesaian: Lihat/Tutup
$\underset{x\to -3}{\mathop{\lim }}\,\frac{\frac{1}{ax}+\frac{1}{3}}{b{{x}^{3}}+27}=-\frac{1}{{{3}^{5}}}$$\underset{x\to -3}{\mathop{\lim }}\,\frac{3+ax}{3ax(b{{x}^{3}}+27)}=-\frac{1}{{{3}^{5}}}$
Untuk $x=-3$ maka:
$3+ax=0\Leftrightarrow 3-3a=0\Leftrightarrow a=1$
Untuk $x=-3$ maka:
$b{{x}^{3}}+27=0\Leftrightarrow b.{{(-3)}^{3}}+27=0\Leftrightarrow b=1$
$a+b=1+1=2$
Jawaban: E
Soal SIMAK UI 2018 - Matematika IPA No. 5
Jika $f(x)$ fungsi kontinu di interval $[1,30]$ dan $\int\limits_{6}^{30}{f(x)dx}=30$, maka $\int\limits_{1}^{9}{f(3y+3)dy}$ = …A. 5
B. 10
C. 15
D. 18
E. 27
Penyelesaian: Lihat/Tutup
Misal:$\int\limits_{y=1}^{y=9}{f(3y+3)dy}$
$x=3y+3$ maka $\frac{dx}{dy}=3\Leftrightarrow dy=\frac{1}{3}dx$
$y=1\Rightarrow x=6$
$y=9\Rightarrow x=30$
$\int\limits_{1}^{9}{f(3y+3)dy}=\int\limits_{6}^{30}{f(x).\frac{1}{3}dx}$
$=\frac{1}{3}\int\limits_{6}^{30}{f(x)dx}$
$=\frac{1}{3}.30=10$
Jawaban: B
Soal SIMAK UI 2018 - Matematika IPA No. 6
Pada balok ABCD.EFGH, dengan AB = 6, BC = 3, dan CG = 2, titik M, N, dan O masing-masing terletak pada rusuk EH, FG, dan AD. Jika 3EM = EH, FN = 2NG, 3DO = 2DA, dan $\alpha$ adalah bidang irisan balok yang melalui M, N, dan O, perbandingan luas bidang $\alpha$ dengan luas permukaan balok adalah …A. $\frac{\sqrt{35}}{36}$
B. $\frac{\sqrt{37}}{36}$
C. $\frac{\sqrt{38}}{36}$
D. $\frac{\sqrt{39}}{36}$
E. $\frac{\sqrt{41}}{36}$
Penyelesaian: Lihat/Tutup
Berdasarkan informasi soal, maka dapat dibuat gambar sebagai berikut:
Bidang $\alpha$ adalah bidang MNN’O (berupa persegipanjang)
Perhatikan segitiga MM’N siku-siku di titik M, dengan MM’ = 6 cm, M’N = 1 cm, maka:
$MN=\sqrt{{{6}^{2}}+{{1}^{1}}}=\sqrt{37}$
Luas bidang $\alpha$ adalah:
$=N'N\times MN$
$=2\sqrt{37}$
Luas permukaan balok adalah:
$=2(p.l+p.t+l.t)$
$=2(6.3+6.2+3.2)=72$
$\frac{\alpha }{L.balok}=\frac{2\sqrt{37}}{72}=\frac{\sqrt{37}}{36}$
Jawaban: B
Soal SIMAK UI 2018 - Matematika IPA No. 7
Diberikan kubus ABCD.EFGH. Sebuah titik P terletak pada rusuk CG sehingga CP : PG = 5 : 2. Jika $\alpha $ adalah sudut terbesar antara rusuk CG dan bidang PBD, maka $\sin \alpha $ = …A. $-\frac{7\sqrt{11}}{33}$
B. $-\frac{7\sqrt{11}}{44}$
C. $\frac{7\sqrt{11}}{33}$
D. $\frac{7\sqrt{11}}{44}$
E. $\frac{7\sqrt{11}}{55}$
Penyelesaian: Lihat/Tutup
Karena CP : PG = 5 : 2 untuk mempermudah perhitungan misalkan panjang rusuk kubus 14 cm, maka CP = 10 cm dan PG = 4 cm. Perhatikan gambar berikut ini!
Sudut terbesar antara rusuk CG dan bidang PBD adalah $\alpha $, dengan $\alpha ={{180}^{o}}-\angle CPQ$
$CQ=7\sqrt{2}$, CP = 10, maka:
$PQ=\sqrt{C{{Q}^{2}}+C{{P}^{2}}}$
$PQ=\sqrt{{{(7\sqrt{2})}^{2}}+{{10}^{2}}}$
$PQ=3\sqrt{22}$
$\sin \alpha =\sin ({{180}^{o}}-\angle CPQ)$
$\sin \alpha =\sin \angle CPQ$
$\sin \alpha =\frac{CQ}{PQ}$
$\sin \alpha =\frac{7\sqrt{2}}{3\sqrt{22}}$
$\sin \alpha =\frac{7}{3\sqrt{11}}\times \frac{\sqrt{11}}{\sqrt{11}}=\frac{7\sqrt{11}}{33}$
Jawaban: C
Soal SIMAK UI 2018 - Matematika IPA No. 8
Jika ${{3}^{x}}+{{5}^{y}}=18$, nilai maksimum ${{3}^{x}}{{.5}^{y}}$ adalah …A. 72
B. 80
C. 81
D. 86
E. 88
Penyelesaian: Lihat/Tutup
${{3}^{x}}+{{5}^{y}}=18$Misal: ${{3}^{x}}=a$ dan ${{3}^{y}}=b$ , maka
$a+b=18\Leftrightarrow a=18-b$ nilai maksimum $ab=...?$
$L=a.b$
$L=a(18-a)$
$L=18a-{{a}^{2}}$
Maksimum/minimum, maka $L'=0$
$18-2a=0\Leftrightarrow a=9$
$L=18a-{{a}^{2}}\Leftrightarrow L=18.9-{{9}^{2}}=81$
Jawaban: C
Soal SIMAK UI 2018 - Matematika IPA No. 9
Diketahui $sx-y=0$ adalah garis singgung sebuah lingkaran yang titik pusatnya di kuadran ketiga dan berjarak 1 satuan ke sumbu-$x$. Jika lingkaran tersebut menyinggung sumbu-$x$ dan titik pusatnya dilalui garis $x=-2$, nilai $3s$ adalah …A. $\frac{1}{6}$
B. $\frac{4}{3}$
C. 3
D. 4
E. 6
Penyelesaian: Lihat/Tutup
Berdasarkan informasi soal, maka dapat dibuat gambar sebagai berikut!
Dari gambar diperoleh:
Lingkaran melalui berpusat di titik (-2,-1) dan berjari-jari 1, maka persamaan lingkarannya adalah:
${{(x+2)}^{2}}+{{(y+1)}^{2}}={{1}^{2}}$, $y=sx$
${{(x+2)}^{2}}+{{(sx+1)}^{2}}=1$
$x^2+4x+4+{{s}^{2}}x^2+2sx+1=1$
$({{s}^{2}}+1)x^2+(2s+4)x+4=0$, syarat menyinggung $D=0$,
${{b}^{2}}-4ac=0$
${{(2s+4)}^{2}}-4({{s}^{2}}+1)4=0$
$4{{s}^{2}}+16s+16-16{{s}^{2}}-16=0$
$-12{{s}^{2}}+16s=0$
$-4s(3s-4)=0$
$-4s=0$ atau $3s=4$
Jawaban: D
Soal SIMAK UI 2018 - Matematika IPA No. 10
Jika kurva $y=(a-2)x^2+\sqrt{3}(1-a)x+a-2$ selalu berada di atas sumbu-$x$, bilangan bulat terkecil $a-2$ yang memenuhi adalah …A. 6
B. 7
C. 8
D. 9
E. 10
Penyelesaian: Lihat/Tutup
$y=(a-2)x^2+\sqrt{3}(1-a)x+a-2$ maka:$A=a-2$, $B=\sqrt{3}(1-a)$, $C=a-2$,
Selalu berada di atas sumbu-X (definit positif), maka:
(1) $A > 0\Leftrightarrow a-2 > 0\Leftrightarrow a>2$
(2) $D < 0$
$B^2-4AC < 0$
${{[\sqrt{3}(1-a)]}^{2}}-4(a-2)(a-2) < 0$
$3(1-2a+{{a}^{2}})-4({{a}^{2}}-4a+4) < 0$
$3-6a+3{{a}^{2}}-4{{a}^{2}}+16a-16 < 0$
$-{{a}^{2}}+10a-13 < 0$
${{a}^{2}}-10a+13 > 0$, dengan rumus abc maka:
$a=\frac{10\pm \sqrt{48}}{2}$
$a=\frac{10\pm 4\sqrt{3}}{2}$
$a=5\pm 2\sqrt{3}$
$a < 5-2\sqrt{3}$ atau $a > 5+2\sqrt{3}$
Dari (1) dan (2) diperoleh batas nilai $a$ adalah:
$a > 5+2\sqrt{3}\Leftrightarrow a > 5+\sqrt{12}$
$a-2 > 5+\sqrt{12}-2$, karena diminta bilangan bulat terkecil, maka:
$a-2=5+\sqrt{16}-2=7$
Jawaban: B
Soal SIMAK UI 2018 - Matematika IPA No. 11
Jika $a+b-c=2$, ${{a}^{2}}+{{b}^{2}}-4{{c}^{2}}=2$, dan $ab=\frac{3}{2}{{c}^{2}}$, nilai $c$ adalah …A. 0
B. 1
C. 2
D. 3
E. 6
Penyelesaian: Lihat/Tutup
$a+b-c=2$$a+b=2+c$
${{(a+b)}^{2}}={{(2+c)}^{2}}$
${{a}^{2}}+{{b}^{2}}+2ab={{c}^{2}}+4c+4$
${{a}^{2}}+{{b}^{2}}-4{{c}^{2}}=2$
-----------------------------------(-)
$2ab+4{{c}^{2}}={{c}^{2}}+4c+2$
$3{{c}^{2}}-4c+2ab-2=0$, diketahui $ab=\frac{3}{2}{{c}^{2}}$
$3{{c}^{2}}-4c+2.\frac{3}{2}{{c}^{2}}-2=0$
$6{{c}^{2}}-4c-2=0$
$3{{c}^{2}}-2c-1=0$
$(3c+1)(c-1)=0$
$c=-\frac{1}{3}$ atau $c=1$
Jawaban: B
Soal SIMAK UI 2018 - Matematika IPA No. 12
Jika ${{S}_{n}}$ adalah jumlah sampai suku ke-n dari barisan geometri, ${{S}_{1}}+{{S}_{6}}=1024$ dan ${{S}_{3}}\times {{S}_{4}}=1023$, maka $\frac{{{S}_{11}}}{{{S}_{8}}}$ = …A. 3
B. 16
C. 32
D. 64
E. 254
Penyelesaian: Lihat/Tutup
Soal Keliru
Gunakan petunjuk C dalam menjawab soal nomor 13 sampai nomor 15.
Petunjuk C yaitu pilihlah:
A. Jika (1), (2), (3) benar.
B. Jika (1) dan (3) benar.
C. Jika (2) dan (4) benar.
D. Jika hanya (4) yang benar.
E. Jika semuanya benar.
Petunjuk C yaitu pilihlah:
A. Jika (1), (2), (3) benar.
B. Jika (1) dan (3) benar.
C. Jika (2) dan (4) benar.
D. Jika hanya (4) yang benar.
E. Jika semuanya benar.
Soal SIMAK UI 2018 - Matematika IPA No. 13
Jika vektor $\vec{u}=(2,-1,2)$ dan $\vec{v}=(4,10,-8)$, maka …(1) $\vec{u}+k\vec{v}$ tegak lurus $\vec{u}$ bila $k=\frac{17}{18}$
(2) sudut antara $\vec{u}$ dan $\vec{v}$ adalah sudut tumpul.
(3) $||pro{{y}_{{\vec{u}}}}\vec{v}||=6$
(4) Jarak antara $\vec{u}$ dan $\vec{v}$ sama dengan $||\vec{u}+\vec{v}||$
Penyelesaian: Lihat/Tutup
Pernyataan (1)$\vec{u}+k\vec{v}$ tegak lurus $\vec{u}$, maka:
$(\vec{u}+k\vec{v}).\vec{u}=0$
$\left( \begin{matrix} 2+4k \\ -1+10k \\ 2-8k \\ \end{matrix} \right).\left( \begin{matrix} 2 \\ -1 \\ 2 \\ \end{matrix} \right)=0$
$4+4k+1-10k+4-16k=0$
$-22k=-9\Leftrightarrow k=\frac{9}{22}$,
Pernyataan (1) SALAH
Pernyataan (2)
$\cos (u,v)=\frac{u.v}{|u||v|}$
$\cos (u,v)=\frac{\left( \begin{matrix} 2 \\ -1 \\ 2 \\ \end{matrix} \right).\left( \begin{matrix} 4 \\ 10 \\ -8 \\ \end{matrix} \right)}{\sqrt{4+1+4}.\sqrt{16+100+64}}$
$\cos (u,v)=\frac{8-10-16}{3.6\sqrt{5}}$
$\cos (u,v)=\frac{-18}{18\sqrt{5}}$, karena nilainya negatif maka sudut antara $\vec{u}$ dan $\vec{v}$ adalah sudut tumpul. Pernyataan (2) BENAR.
Berdasarkan petunjuk C, tanpa mengecek pernyataan (4) maka opsi yang memenuhi adalah C.
Jawaban: C
Soal SIMAK UI 2018 - Matematika IPA No. 14
Jika $y=\frac{1}{3}{{x}^{3}}-ax+b$, $a > 0$, dan $a,b\in R$, maka …(1) nilai minimum lokal $y=b-\frac{2}{3}{{a}^{\frac{3}{2}}}$
(2) nilai maksimum lokal $y=b+\frac{2}{3}{{a}^{\frac{3}{2}}}$
(3) $y$ stasioner saat $x={{a}^{\frac{1}{2}}}$
(4) naik pada interval $\left[ -\infty ,-{{a}^{\frac{1}{2}}} \right]$
Penyelesaian: Lihat/Tutup
$y=\frac{1}{3}{{x}^{3}}-ax+b$$\frac{dy}{dx}=x^2-a=0$, karena $a > 0$ maka:
$(x+\sqrt{a})(x-\sqrt{a})=0$
$x=-\sqrt{a}$ atau $x=\sqrt{a}$,
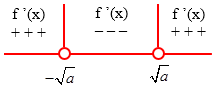
Dari gambar garis bilangan, maka: pernyataan (3) dan (4) BENAR.
$y=\frac{1}{3}{{x}^{3}}-ax+b$
$x=-\sqrt{a}\Rightarrow y=b+\frac{2}{3}{{a}^{\frac{3}{2}}}$ (nilai maksimum lokal), pernyataan (1) BENAR.
$x=\sqrt{a}\Rightarrow y=b-\frac{2}{3}{{a}^{\frac{3}{2}}}$ (nilai minimum lokal), pernyataan (2) BENAR.
Jawaban: E
Soal SIMAK UI 2018 - Matematika IPA No. 15
Jika $\alpha =-\frac{\pi }{12}$, maka …(1) ${{\sin }^{4}}\alpha +{{\cos }^{4}}\alpha =\frac{6}{8}$
(2) ${{\sin }^{6}}\alpha +{{\cos }^{6}}\alpha =\frac{12}{16}$
(3) ${{\cos }^{4}}\alpha =\frac{1}{2}-\frac{1}{4}\sqrt{3}$
(4) ${{\sin }^{4}}\alpha =\frac{7}{16}-\frac{1}{4}\sqrt{3}$
Penyelesaian: Lihat/Tutup
$\alpha =-\frac{\pi }{12}=-{{15}^{o}}$$\sin {{15}^{o}}=\sin ({{45}^{o}}-{{30}^{o}})$
$\sin {{15}^{o}}=\sin {{45}^{o}}\cos {{30}^{o}}-\cos {{45}^{o}}\sin {{30}^{o}}$
$\sin {{15}^{o}}=\frac{1}{2}\sqrt{2}.\frac{1}{2}\sqrt{3}-\frac{1}{2}\sqrt{2}.\frac{1}{2}$
$\sin {{15}^{o}}=\frac{\sqrt{6}-\sqrt{2}}{4}$
${{\sin }^{2}}{{15}^{o}}={{\left( \frac{\sqrt{6}-\sqrt{2}}{4} \right)}^{2}}$
${{\sin }^{2}}{{15}^{o}}=\frac{2-\sqrt{3}}{4}$
${{\sin }^{4}}{{15}^{o}}={{\left( \frac{2-\sqrt{3}}{4} \right)}^{2}}=\frac{7}{16}-\frac{1}{4}\sqrt{3}$, pernyataan (4) BENAR.
Dengan cara yang sama:
$\cos {{15}^{o}}=\frac{\sqrt{6}+\sqrt{2}}{4}$
${{\cos }^{2}}{{15}^{o}}=\frac{2+\sqrt{3}}{4}$
${{\cos }^{4}}{{15}^{o}}={{\left( \frac{2+\sqrt{3}}{4} \right)}^{2}}=\frac{7}{16}-\frac{1}{4}\sqrt{3}$, pernyataan (3) SALAH.
Dengan logika, berdasarkan petunjuk C maka kita sudah dapat menentukan opsi yang memenuhi adalah D.
Jawaban: D

how about no 12?
ReplyDeleteNo 10 kok dr akar 12 jadi akar 16 ya ?
ReplyDeletePada pembahasan sudah dijelaskan. Pada soal diminta bilangan bulat terkecil. Nah $\sqrt{12}$ bukan bilangan bulat, maka bilangan bulat terkecil yang lebih besar dari $\sqrt{12}$ adalah $\sqrt{16}$.
Deletekalo bilangan bulat terkecil kenapa enggak pake yang akar 9 yang lebih kecil dari akar 12 dan akar 16
DeletePertanyaannya? Bilangan bulat terkecil yang lebih dari (>)
Delete