Pembahasan Soal SIMAK UI 2012 Matematika Dasar Kode 223
Berikut ini saya share soal dan pembahasan Matematika Dasar SIMAK UI Tahun 2012 untuk bahan belajar teman-teman berlatih soal-soal SIMAK UI, sehingga peluang untuk bisa diterima semakin besar. Sebelum membaca pembahasan ini, sebaiknya kalian download soalnya terlebih dahulu, dijawab secara mandiri, setelah itu kamu periksa jawaban kamu melalui pembahasan ini.
Download Soal Matematika Dasar SIMAK UI 2012 Kode 223
Matematika Dasar SIMAK UI 2012 No. 1
Jika $4\sin x-\frac{4}{\cos x}=-1$, maka diskriminan dari persamaan kuadrat $(\sin x){{a}^{2}}+\sqrt{\cos x}.a-\cos x=0$ adalah …
A. -4 B. -2 C. 0 D. 2 E. 4
Pembahasan:
$4\sin x-\frac{4}{\cos x}=-1$
$4\sin x.\cos x-4=-\cos x$
$4\sin x.\cos x+\cos x=4$
Diskriminan dari persamaan:
$(\sin x){{a}^{2}}+\sqrt{\cos x}.a-\cos x=0$
$A=\sin x$, $B=\sqrt{\cos x}$, $C=-\cos x$
$D={{B}^{2}}-4AC$
$D={{(\sqrt{\cos x})}^{2}}-4.\sin x.(-\cos x)$
$D=\cos x+4.\sin x.\cos x$
$D=4$
Jawaban: E
Matematika Dasar SIMAK UI 2012 No. 2
Jika f(2) = 3, f ‘(2) = 4, g(2) = 2, dan g’(2) = 5, maka untuk x = 2, nilai dari $\frac{\frac{d}{dx}[{{f}^{2}}(x)+{{g}^{3}}(x)]}{\frac{d}{dx}[f(g(x))]}$ adalah …
A. 3,6 B. 4,2 C. 4,8 D. 5,6 E. 7
Pembahasan:
f(2) = 3, f ‘(2) = 4, g(2) = 2, dan g’(2) = 5
$\frac{\frac{d}{dx}[{{f}^{2}}(x)+{{g}^{3}}(x)]}{\frac{d}{dx}[f(g(x))]}$
$=\frac{2f(x).f'(x)+3{{g}^{2}}(x).g'(x)}{g'(x).f'(g(x))}$
x = 2, maka:
$=\frac{2f(2).f'(2)+3{{g}^{2}}(2).g'(2)}{g'(2).f'(g(x2))}$
$=\frac{2.3.4+{{3.2}^{2}}.5}{5.4}=4,2$
Jawaban: B
Matematika Dasar SIMAK UI 2012 No. 3
Jika ${{(a+b+c+d+e+f+g+h+i+j)}^{2}}$ diuraikan dan disederhakan, maka banyaknya suku yang berbeda adalah …
A. 10 B. 20 C. 45 D. 55 E. 100
Pembahasan:
Banyak suku dari ${{(a+b+c+d+e+f+g+h+i+j)}^{2}}$ adalah:
Suku yang terdiri dari satu variabel ada sebanyak:
${}_{10}{{C}_{1}}=\frac{10!}{1!.(10-1)!}=\frac{10.9!}{1.9!}=10$
Suku yang terdiri dari dua variabel ada sebanyak:
${}_{10}{{C}_{2}}=\frac{10!}{2!.(10-2)!}=\frac{10.9.8!}{2.1.8!}=45$
Jadi, banyak suku seluruhnya adalah 10 + 45 = 55.
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 4
Ahmad dan Aisyah teman satu sekolah di sebuah SMA di kota Depok. Saat ini mereka duduk di kelas 1. Mereka mencatat jumlah seluruh siswa kelas 1 di sekolah mereka. Aisyah mencatat, 5/17 dari temannya di kelas 1 adalah laki-laki, sedangkan menurut catatan Ahmad, 2/7 dari temannya di kelas 1 adalah laki-laki. Jika catatan mereka berdua tidak salah, maka banyaknya jumlah siswa perempuan kelas 1 di sekolah mereka adalah …
A. 35 B. 55 C. 65 D. 85 E. 120
Pembahasan:
Misal, jumlah siswa seluruhnya = n, dan banyak siswa laki-laki = L maka:
Data Aisyah:
5/17 dari temannya, teman Aisyah = n -1 maka:
$\frac{5}{17}(n-1)=L$
Data Ahmad:
2/7 dari temannya (n – 1) di kelas 1 adalah laki-laki (L-1, sebab Ahmad tidak termasuk), maka:
$\frac{2}{7}(n-1)=L-1$
$\frac{2}{7}(n-1)+1=L$
$\frac{2}{7}(n-1)+1=\frac{5}{17}(n-1)$
$\left( \frac{2}{7}-\frac{5}{17} \right)(n-1)=-1$
$\left( \frac{-1}{119} \right)(n-1)=-1$
$n-1=119\Leftrightarrow n=120$
$L=\frac{5}{17}(n-1)\Leftrightarrow L=\frac{5}{17}(120-1)=35$
Perempuan = 120 - 35 = 85 orang.
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 5
Jika $-3\le x\le 4$, $-2\le y\le 5$, $4\le z\le 10$, dan $w=z-xy$, maka nilai terbesar yang mungkin untuk $w$ adalah …
A. 10 B. 16 C. 18 D. 25 E. 30
Pembahasan:
$-3\le x\le 4$
$-2\le y\le 5$
$4\le z\le 10$
$w=z-xy$ maka agar w maksimum maka nilai z = 10,
Agar w maksimum maka xy harus minimum
Itu diperoleh jika x = -3 dan y = 5, maka xy = -15
${{w}_{maks}}=z-xy\Leftrightarrow w=10-(-15)=25$
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 6
Jika $\sqrt{2+2\cos 2x}=\frac{3}{\sqrt{1+4\cos 2x}}$ untuk $0 < x < 2\pi$, $4\cos 2x\ne -1$, maka jumlah nilai x yang memenuhi adalah ….
A. ${{720}^{o}}$
B. ${{480}^{o}}$
C. ${{390}^{o}}$
D. ${{360}^{o}}$
E. ${{240}^{o}}$
Pembahasan:
$\sqrt{2+2\cos 2x}=\frac{3}{\sqrt{1+4\cos 2x}}$
$2+2\cos 2x=\frac{9}{1+4\cos 2x}$
Misal: cos 2x = p, maka:
$2+2p=\frac{9}{1+4p}$
$2+8p+2p+8{{p}^{2}}=9$
$8{{p}^{2}}+10p-7=0$
$(4p+7)(2p-1)=0$
$p=-\frac{7}{4}$ atau $p=\frac{1}{2}$
$p=-\frac{7}{4}\Rightarrow \cos 2x=-\frac{7}{4}(TM)$
$p=\frac{1}{2}$, maka:
$\cos 2x=\frac{1}{2}$
$\cos 2x=\cos {{60}^{o}}$
$2x=\pm {{60}^{o}}+k{{.360}^{o}}$
$x=\pm {{30}^{o}}+k{{.180}^{o}}$
$k=0\Rightarrow {{x}_{1}}={{30}^{o}}$
$k=1\Rightarrow {{x}_{2}}={{210}^{o}},{{x}_{3}}={{150}^{o}}$
$k=2\Rightarrow {{x}_{4}}={{330}^{o}}$
Jumlah semua x adalah:
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}={{720}^{o}}$
Jawaban: A
Matematika Dasar SIMAK UI 2012 No. 1
Jika $4\sin x-\frac{4}{\cos x}=-1$, maka diskriminan dari persamaan kuadrat $(\sin x){{a}^{2}}+\sqrt{\cos x}.a-\cos x=0$ adalah …
A. -4 B. -2 C. 0 D. 2 E. 4
Pembahasan:
$4\sin x-\frac{4}{\cos x}=-1$
$4\sin x.\cos x-4=-\cos x$
$4\sin x.\cos x+\cos x=4$
Diskriminan dari persamaan:
$(\sin x){{a}^{2}}+\sqrt{\cos x}.a-\cos x=0$
$A=\sin x$, $B=\sqrt{\cos x}$, $C=-\cos x$
$D={{B}^{2}}-4AC$
$D={{(\sqrt{\cos x})}^{2}}-4.\sin x.(-\cos x)$
$D=\cos x+4.\sin x.\cos x$
$D=4$
Jawaban: E
Matematika Dasar SIMAK UI 2012 No. 2
Jika f(2) = 3, f ‘(2) = 4, g(2) = 2, dan g’(2) = 5, maka untuk x = 2, nilai dari $\frac{\frac{d}{dx}[{{f}^{2}}(x)+{{g}^{3}}(x)]}{\frac{d}{dx}[f(g(x))]}$ adalah …
A. 3,6 B. 4,2 C. 4,8 D. 5,6 E. 7
Pembahasan:
f(2) = 3, f ‘(2) = 4, g(2) = 2, dan g’(2) = 5
$\frac{\frac{d}{dx}[{{f}^{2}}(x)+{{g}^{3}}(x)]}{\frac{d}{dx}[f(g(x))]}$
$=\frac{2f(x).f'(x)+3{{g}^{2}}(x).g'(x)}{g'(x).f'(g(x))}$
x = 2, maka:
$=\frac{2f(2).f'(2)+3{{g}^{2}}(2).g'(2)}{g'(2).f'(g(x2))}$
$=\frac{2.3.4+{{3.2}^{2}}.5}{5.4}=4,2$
Jawaban: B
Matematika Dasar SIMAK UI 2012 No. 3
Jika ${{(a+b+c+d+e+f+g+h+i+j)}^{2}}$ diuraikan dan disederhakan, maka banyaknya suku yang berbeda adalah …
A. 10 B. 20 C. 45 D. 55 E. 100
Pembahasan:
Banyak suku dari ${{(a+b+c+d+e+f+g+h+i+j)}^{2}}$ adalah:
Suku yang terdiri dari satu variabel ada sebanyak:
${}_{10}{{C}_{1}}=\frac{10!}{1!.(10-1)!}=\frac{10.9!}{1.9!}=10$
Suku yang terdiri dari dua variabel ada sebanyak:
${}_{10}{{C}_{2}}=\frac{10!}{2!.(10-2)!}=\frac{10.9.8!}{2.1.8!}=45$
Jadi, banyak suku seluruhnya adalah 10 + 45 = 55.
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 4
Ahmad dan Aisyah teman satu sekolah di sebuah SMA di kota Depok. Saat ini mereka duduk di kelas 1. Mereka mencatat jumlah seluruh siswa kelas 1 di sekolah mereka. Aisyah mencatat, 5/17 dari temannya di kelas 1 adalah laki-laki, sedangkan menurut catatan Ahmad, 2/7 dari temannya di kelas 1 adalah laki-laki. Jika catatan mereka berdua tidak salah, maka banyaknya jumlah siswa perempuan kelas 1 di sekolah mereka adalah …
A. 35 B. 55 C. 65 D. 85 E. 120
Pembahasan:
Misal, jumlah siswa seluruhnya = n, dan banyak siswa laki-laki = L maka:
Data Aisyah:
5/17 dari temannya, teman Aisyah = n -1 maka:
$\frac{5}{17}(n-1)=L$
Data Ahmad:
2/7 dari temannya (n – 1) di kelas 1 adalah laki-laki (L-1, sebab Ahmad tidak termasuk), maka:
$\frac{2}{7}(n-1)=L-1$
$\frac{2}{7}(n-1)+1=L$
$\frac{2}{7}(n-1)+1=\frac{5}{17}(n-1)$
$\left( \frac{2}{7}-\frac{5}{17} \right)(n-1)=-1$
$\left( \frac{-1}{119} \right)(n-1)=-1$
$n-1=119\Leftrightarrow n=120$
$L=\frac{5}{17}(n-1)\Leftrightarrow L=\frac{5}{17}(120-1)=35$
Perempuan = 120 - 35 = 85 orang.
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 5
Jika $-3\le x\le 4$, $-2\le y\le 5$, $4\le z\le 10$, dan $w=z-xy$, maka nilai terbesar yang mungkin untuk $w$ adalah …
A. 10 B. 16 C. 18 D. 25 E. 30
Pembahasan:
$-3\le x\le 4$
$-2\le y\le 5$
$4\le z\le 10$
$w=z-xy$ maka agar w maksimum maka nilai z = 10,
Agar w maksimum maka xy harus minimum
Itu diperoleh jika x = -3 dan y = 5, maka xy = -15
${{w}_{maks}}=z-xy\Leftrightarrow w=10-(-15)=25$
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 6
Jika $\sqrt{2+2\cos 2x}=\frac{3}{\sqrt{1+4\cos 2x}}$ untuk $0 < x < 2\pi$, $4\cos 2x\ne -1$, maka jumlah nilai x yang memenuhi adalah ….
B. ${{480}^{o}}$
C. ${{390}^{o}}$
D. ${{360}^{o}}$
E. ${{240}^{o}}$
Pembahasan:
$\sqrt{2+2\cos 2x}=\frac{3}{\sqrt{1+4\cos 2x}}$
$2+2\cos 2x=\frac{9}{1+4\cos 2x}$
Misal: cos 2x = p, maka:
$2+2p=\frac{9}{1+4p}$
$2+8p+2p+8{{p}^{2}}=9$
$8{{p}^{2}}+10p-7=0$
$(4p+7)(2p-1)=0$
$p=-\frac{7}{4}$ atau $p=\frac{1}{2}$
$p=-\frac{7}{4}\Rightarrow \cos 2x=-\frac{7}{4}(TM)$
$p=\frac{1}{2}$, maka:
$\cos 2x=\frac{1}{2}$
$\cos 2x=\cos {{60}^{o}}$
$2x=\pm {{60}^{o}}+k{{.360}^{o}}$
$x=\pm {{30}^{o}}+k{{.180}^{o}}$
$k=0\Rightarrow {{x}_{1}}={{30}^{o}}$
$k=1\Rightarrow {{x}_{2}}={{210}^{o}},{{x}_{3}}={{150}^{o}}$
$k=2\Rightarrow {{x}_{4}}={{330}^{o}}$
Jumlah semua x adalah:
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}={{720}^{o}}$
Jawaban: A
Matematika Dasar SIMAK UI 2012 No. 7
Banyaknya bilangan ratusan kelipatan 5 yang dapat disusun dari digit 0, 1, 2, 3, 4, 5 dengan digit yang berbeda adalah …
A. 24 B. 30 C. 32 D. 36 E. 40
Pembahasan:
Dengan pengisian tempat yang tersedia, misalkan bilangan itu adalah ABC.
A = angka ratusan, B = angka puluhan, dan C = angka satuan.
Langkah:
1. pilih angka untuk satuan (C)
2. pilih angka untuk ratusan (A)
3. pilih angka untuk puluhan (B)
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 8
Jika diketahui $x$ dan $y$ adalah bilangan riil dengan $x > 1$ dan $y > 0.$ Jika $xy={{x}^{y}}$ dan $\frac{x}{y}={{x}^{5y}}$ maka ${{x}^{2}}+3y$ = …
A. 29 B. 28 C. 27 D. 26 E. 25
Pembahasan:
$x > 0$ dan $y > 0$
$xy={{x}^{y}}$
$y={{x}^{y-1}}$ … (1)
$\frac{x}{y}={{x}^{5y}}$
$x={{x}^{5y}}.y$
$x={{x}^{5y}}.{{x}^{y-1}}$
${{x}^{1}}={{x}^{6y-1}}$
$1=6y-1$
$2=6y\Leftrightarrow y=\frac{2}{6}=\frac{1}{3}$
$y={{x}^{y-1}}$
$\frac{1}{3}={{x}^{\frac{1}{3}-1}}$
$\frac{1}{3}=\frac{1}{{{x}^{\frac{2}{3}}}}$
${{x}^{\frac{2}{3}}}=3\Leftrightarrow x={{3}^{\frac{3}{2}}}$
maka,
${{x}^{2}}+3y={{\left( {{3}^{\frac{3}{2}}} \right)}^{2}}+3.\frac{1}{3}=27+1=28$
Jawaban: B
Matematika Dasar SIMAK UI 2012 No. 9
Dalam sebuah bujur sangkar dibuat empat buah persegipanjang yang sama sehingga terdapat bujursangkar kecil di dalamnya (seperti tampak dalam gambar). Jika diketahui luas bujursangkar besar adalah sembilan kali lebih besar dari luas bujursangkar kecil, maka perbandingan sisi panjang dan sisi pendek dari persegi panjang adalah ….
A. $\frac{5}{4}$ B. $\frac{4}{3}$ C. $\frac{3}{2}$ D. 2 E. $\frac{5}{2}$
Pembahasan:
Luas bujur sangkar besar = 9 x Luas bujur sangkar kecil
Maka: ${{s}_{b}}=3;{{s}_{k}}=1$
A. $\frac{5}{4}$ B. $\frac{4}{3}$ C. $\frac{3}{2}$ D. 2 E. $\frac{5}{2}$
Pembahasan:
Luas bujur sangkar besar = 9 x Luas bujur sangkar kecil
Maka: ${{s}_{b}}=3;{{s}_{k}}=1$
Jadi, $\frac{sisiterpanjang}{sisiterpendek}=\frac{2}{1}=2$
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 10
Dua parabola mempunyai titik puncak yang sama. Parabola pertama memotong sumbu X di titik (a, 0) dan (b, 0) serta memotong sumbu Y di (0, -32). Parabola kedua definitif positif dan memotong sumbu Y di titik (0, 40). Jika a dan b dua bilangan bulat positif pertama yang habis dibagi 4, maka persamaan parabola kedua adalah …
A. $y={{x}^{2}}+40$
B. $y={{x}^{2}}-30$
C. $y={{x}^{2}}-12x-32$
D. $y={{x}^{2}}+12x+40$
E. $y={{x}^{2}}-12x+40$
Pembahasan:
a dan b dua bilangan bulat positif pertama yang habis dibagi 4, diperoleh a = 4 dan b = 8.
parabola I (${{y}_{1}}$) memotong sumbu X di $(4,0)$ dan $(8,0)$ maka:
${{y}_{1}}=k(x-4)(x-8)$, melalui titik $(0,-32)$
$-32=k(0-4)(0-8)$
$-32=32k\Leftrightarrow k=-1$
${{y}_{1}}=-1(x-4)(x-8)$
Puncak ${{y}_{1}}$ di $x=\frac{4+8}{2}=6$
${{y}_{1}}=-1(6-4)(6-8)=4$
Puncak ${{y}_{1}}$ sama dengan puncak parabola II (${{y}_{2}}$) yaitu di $(6,4)$, maka:
${{y}_{2}}=p{{(x-6)}^{2}}+4$ melalui titik $(0,40)$
$40=p{{(0-6)}^{2}}+4\Leftrightarrow p=1$
${{y}_{2}}=1{{(x-6)}^{2}}+4$
${{y}_{2}}={{x}^{2}}-12x+40$
Jawaban: E
Matematika Dasar SIMAK UI 2012 No. 11
Jika garis singgung parabola $y=4x-{{x}^{2}}$ di titik M(1, 3) juga merupakan garis singgung parabola $y={{x}^{2}}-6x+k$, maka nilai dari $5-\sqrt{k-1}$ adalah …
A. 0 B. 1 C. 2 D. 3 E. 4
Pembahasan:
Persamaan garis singgung Parabola I:
$y=4x-{{x}^{2}}$
$y'=4-2x$ di titik M(1, 3) adalah:
$m={{\left. y' \right|}_{x=1}}\Leftrightarrow m=4-2.1=2$
$y-{{y}_{1}}=m(x-{{x}_{1}})$
$y-3=2(x-1)$
$y=2x+1$
Persamaan garis singgung Parabola II sama dengan garis singgung parabola I:
$y={{x}^{2}}-6x+k$
$y'=2x-6\Leftrightarrow 2=2x-6\Leftrightarrow {{x}_{2}}=4$
Garis singgungnya:
$y=2x+1\Leftrightarrow {{y}_{2}}=2.4+1=9$
$y={{x}^{2}}-6x+k$ melalui titik $(4,9)$ maka:
$9={{4}^{2}}-6.4+k\Leftrightarrow k=17$
$5-\sqrt{k-1}=5-\sqrt{17-1}=1$
Jawaban: B
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 10
Dua parabola mempunyai titik puncak yang sama. Parabola pertama memotong sumbu X di titik (a, 0) dan (b, 0) serta memotong sumbu Y di (0, -32). Parabola kedua definitif positif dan memotong sumbu Y di titik (0, 40). Jika a dan b dua bilangan bulat positif pertama yang habis dibagi 4, maka persamaan parabola kedua adalah …
A. $y={{x}^{2}}+40$
B. $y={{x}^{2}}-30$
C. $y={{x}^{2}}-12x-32$
D. $y={{x}^{2}}+12x+40$
E. $y={{x}^{2}}-12x+40$
Pembahasan:
a dan b dua bilangan bulat positif pertama yang habis dibagi 4, diperoleh a = 4 dan b = 8.
parabola I (${{y}_{1}}$) memotong sumbu X di $(4,0)$ dan $(8,0)$ maka:
${{y}_{1}}=k(x-4)(x-8)$, melalui titik $(0,-32)$
$-32=k(0-4)(0-8)$
$-32=32k\Leftrightarrow k=-1$
${{y}_{1}}=-1(x-4)(x-8)$
Puncak ${{y}_{1}}$ di $x=\frac{4+8}{2}=6$
${{y}_{1}}=-1(6-4)(6-8)=4$
Puncak ${{y}_{1}}$ sama dengan puncak parabola II (${{y}_{2}}$) yaitu di $(6,4)$, maka:
${{y}_{2}}=p{{(x-6)}^{2}}+4$ melalui titik $(0,40)$
$40=p{{(0-6)}^{2}}+4\Leftrightarrow p=1$
${{y}_{2}}=1{{(x-6)}^{2}}+4$
${{y}_{2}}={{x}^{2}}-12x+40$
Jawaban: E
Matematika Dasar SIMAK UI 2012 No. 11
Jika garis singgung parabola $y=4x-{{x}^{2}}$ di titik M(1, 3) juga merupakan garis singgung parabola $y={{x}^{2}}-6x+k$, maka nilai dari $5-\sqrt{k-1}$ adalah …
A. 0 B. 1 C. 2 D. 3 E. 4
Pembahasan:
Persamaan garis singgung Parabola I:
$y=4x-{{x}^{2}}$
$y'=4-2x$ di titik M(1, 3) adalah:
$m={{\left. y' \right|}_{x=1}}\Leftrightarrow m=4-2.1=2$
$y-{{y}_{1}}=m(x-{{x}_{1}})$
$y-3=2(x-1)$
$y=2x+1$
Persamaan garis singgung Parabola II sama dengan garis singgung parabola I:
$y={{x}^{2}}-6x+k$
$y'=2x-6\Leftrightarrow 2=2x-6\Leftrightarrow {{x}_{2}}=4$
Garis singgungnya:
$y=2x+1\Leftrightarrow {{y}_{2}}=2.4+1=9$
$y={{x}^{2}}-6x+k$ melalui titik $(4,9)$ maka:
$9={{4}^{2}}-6.4+k\Leftrightarrow k=17$
$5-\sqrt{k-1}=5-\sqrt{17-1}=1$
Jawaban: B
Matematika Dasar SIMAK UI 2012 No. 12
$\frac{{{x}^{2}}+2x-3}{{{x}^{2}}-x-6}\ge 0$
$\frac{(x+3)(x-1)}{(x-3)(x+2)}\ge 0$
Himpunan penyelesaian dari pertidaksamaan berikut, $\sqrt{\frac{{{x}^{2}}+2x-3}{{{x}^{2}}-x-6}} < \left| \frac{x-1}{x+2} \right|$ adalah …
A. {$x|x < -3 \cup -2 < x \le -\frac{1}{3}, x \in R$}
B. {$x|x \le -3 \cup -2 < x < -\frac{1}{3}, x \in R$}
C. {$x|x < -\frac{1}{3} \cup 1 < x < 3, x \in R$}
D. {$x|x \le -3 \cup -2 < x \le 1, x \in R$}
E. {$x|-3 \le x < -2 \cup 1 \le x < 3, x \in R$}
Pembahasan:
(i)$\frac{{{x}^{2}}+2x-3}{{{x}^{2}}-x-6}\ge 0$
$\frac{(x+3)(x-1)}{(x-3)(x+2)}\ge 0$
$x\ge -3$ atau $-2 < x \le 1$ atau $x > 3$
(ii)
$\sqrt{\frac{{{x}^{2}}+2x-3}{{{x}^{2}}-x-6}} < \left| \frac{x-1}{x+2} \right|$
$\frac{{{x}^{2}}+2x-3}{{{x}^{2}}-x-6} < \frac{{{\left( x-1 \right)}^{2}}}{{{\left( x+2 \right)}^{2}}}$
$\frac{(x+3)(x-1)}{(x-3)(x+2)}-\frac{{{\left( x-1 \right)}^{2}}}{{{\left( x+2 \right)}^{2}}} < 0$
$\frac{(x+3)(x-1)(x+2)}{(x-3)(x+2)(x+2)}-\frac{{{\left( x-1 \right)}^{2}}(x-3)}{{{\left( x+2 \right)}^{2}}(x-3)} < 0$
$\frac{(3x+1)(x-1)}{{{\left( x+2 \right)}^{2}}(x-3)} < 0$
$x < \frac{1}{3}$ atau $1 < x < 3$, $x\ne -2$
Dari (i) dan (ii) maka diperoleh penyelesaian:
$x \le -3$ atau $-2 < x < -\frac{1}{3}$
Jawaban: B
Matematika Dasar SIMAK UI 2012 No. 13
Jika kedua akar persamaan $p{{x}^{2}}+8x+3p=0$ bernilai negatif, maka jumlah kuadrat kedua akar-akar tersebut bernilai …
A. maksimum 30
B. minimum 30
C. minimum 6
D. maksimum 6
E. minimum -15/2
Pembahasan:
$p{{x}^{2}}+8x+3p=0$, ${{x}_{1}} < 0$ dan ${{x}_{2}} < 0$
1) ${{x}_{1}}+{{x}_{2}} < 0 \Leftrightarrow \frac{-8}{p} < 0\Leftrightarrow p > 0$
2) ${{x}_{1}}.{{x}_{2}} > 0 \Leftrightarrow \frac{3p}{p} > 0 \Leftrightarrow 3 > 0$ (memenuhi)
3) $D\ge 0\Leftrightarrow {{b}^{2}}-4ac\ge 0$
${{8}^{2}}-4.p.3p\ge 0$
$64-12{{p}^{2}}\ge 0$
$3{{p}^{2}}-16\le 0$
${{p}^{2}}\le \frac{16}{3}\Leftrightarrow \frac{1}{{{p}^{2}}}\le \frac{3}{16}$
$\begin{align}x_{1}^{2}+x_{2}^{2}&={{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-2{{x}_{1}}.{{x}_{2}} \\ & ={{\left( \frac{-8}{p} \right)}^{2}}-2.\frac{3p}{p} \\ & =\frac{64}{{{p}^{2}}}-6 \\ {{(x_{1}^{2}+x_{2}^{2})}_{\min }}&=64.\frac{3}{16}-6=6 \end{align}$
Jawaban: C
Matematika Dasar SIMAK UI 2012 No. 14
Sebuah lingkaran memiliki jari-jari $\log {{a}^{2}}$ dan keliling $\log {{b}^{4}}$, maka ${}^{a}\log b$ = …
A. $\frac{1}{4\pi }$ B. $\frac{1}{\pi }$ C. $\pi $ D. $2\pi $ E. ${{10}^{2\pi }}$
Pembahasan:
$r=\log {{a}^{2}}$
$\begin{align} k&=\log {{b}^{4}} \\ 2\pi r &=\log {{b}^{4}} \\ 2\pi .\log {{a}^{2}} &=\log {{b}^{4}} \\ 2\pi .2.\log a &=4.\log b \\ \pi .\log a &=\log b \\ \pi &=\frac{\log b}{\log a} \\ {}^{a}\log b &=\pi \end{align}$
Jawaban: C
Matematika Dasar SIMAK UI 2012 No. 15
Misalkan a dan b adalah sudut lancip yang dibentuk oleh sumbu X dengan garis singgung kurva $y=-{{x}^{2}}+6x-8$ di titik potong kurva tersebut dengan garis $y=2x-5$, maka $\sin (a-b)$ = …
A. $\frac{1}{4}$
B. $\frac{1}{2}$
C. $\frac{3}{\sqrt{15}}$
D. $\frac{4}{17}\sqrt{17}$
E. 4
Pembahasan:
*) Titik potong
$y=-{{x}^{2}}+6x-8$ dan $y=2x-5$
$-{{x}^{2}}+6x-8=2x-5$
$-{{x}^{2}}+4x-3=0$
${{x}^{2}}-4x+3=0$
$(x-1)(x-3)=0$
${{x}_{1}}=1$ atau ${{x}_{2}}=3$
*) Menentukan tan a dan tan b
$y=-{{x}^{2}}+6x-8$
$y'=-2x+6$
$\tan a=y'{{|}_{x=1}}=-2.1+6=4$
$\tan b=y'{{|}_{x=3}}=-2.3+6=0$
$\tan (a-b)=\frac{\tan a-\tan b}{1+\tan a.\tan b}$
$\tan (a-b)=\frac{4-0}{1+4.0}=\frac{4}{1}=\frac{de}{sa}$
$mi=\sqrt{d{{e}^{2}}+s{{a}^{2}}}=\sqrt{{{4}^{2}}+{{1}^{2}}}=\sqrt{17}$
$\sin (a-b)=\frac{de}{mi}=\frac{4}{\sqrt{17}}=\frac{4}{17}\sqrt{17}$
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 16
Jika titik A(a, c) dan B(b, d) adalah dua titik berbeda yang terletak pada kurva $y={{x}^{2}}+x+3$, maka garis AB akan memotong sumbu Y pada …
A. $y=\frac{a+b+3}{ab-3}$
B. $y={{a}^{2}}+a+3$
C. $y={{b}^{2}}+b+3$
D. $y={{a}^{2}}-{{b}^{2}}+3$
E. $y=3-ab$
Pembahasan:
$y={{x}^{2}}+x+3$
$A(a,c)\Rightarrow c={{a}^{2}}+a+3$
$B(b,d)\Rightarrow d={{b}^{2}}+b+3$
Kurangkan kedua persamaan maka:
$d-c=({{b}^{2}}+b+3)-({{a}^{2}}+a+3)$
$d-c={{b}^{2}}-{{a}^{2}}+b-a$
$d-c=(b+a)(b-a)+(b-a)$
Persamaan garis yang melalui titik A dan titik B
$y-c=\left( \frac{d-c}{b-a} \right)(x-a)$
Menentukan titik potong sumbu Y
$y=\left( \frac{d-c}{b-a} \right)(x-a)+c$
$y=\left( \frac{(b+a)(b-a)+(b-a)}{b-a} \right)(0-a)+c$
$y=\left( b+a+1 \right)(-a)+{{a}^{2}}+a+3$
$y=-ab-{{a}^{2}}-a+{{a}^{2}}+a+3$
$y=3-ab$
Jawaban: E
Matematika Dasar SIMAK UI 2012 No. 17
Misalkan rata-rata nilai ujian matematika dari 30 siswa adalah 8,4. Jika nilai yang terkecil tidak diperhitungkan, maka rata-ratanya menjadi 8,5, sedangkan jika nilai terbesarnya tidak diperhitungkan, maka rata-ratanya menjadi 8,2. Jangkauan dari nilai ujian matematika adalah …
A. 6,7 B. 7,4 C. 7,8 D. 8,2 E. 8,7
Pembahasan:
Misalkan data: ${{x}_{1}},{{x}_{2}},{{x}_{3}},...,{{x}_{30}}$, maka:
${{x}_{30}}=30(8,4)-29(8,2)=14,2$
${{x}_{1}}=30(8,4)-29(8,5)=5,5$
Jangkauan = ${{x}_{30}}-{{x}_{1}}=14,2-5,5=8,7$
Jawaban: E
Gunakan petunjuk C dalam menjawab soal nomor 18 sampai 20.
Matematika Dasar SIMAK UI 2012 No. 18
Apabila $k=x+y$, maka ${{k}^{2}}-k=1$ dan apabila $k=x-y$, maka ${{k}^{2}}+k=1$, maka $x+y$ = …
(1) $\frac{1}{2}+\frac{1}{2}\sqrt{5}$
(2) $\frac{1}{2}$
(3) $\frac{1}{2}-\frac{1}{2}\sqrt{5}$
(4) $\frac{1}{2}\sqrt{5}$
Pembahasan:
$k=x+y$, maka:
${{k}^{2}}-k=1$
${{(x+y)}^{2}}-(x+y)=1$
${{x}^{2}}+{{y}^{2}}+2xy-x-y=1$ …. (1)
$k=x-y$, maka:
${{(x-y)}^{2}}+(x-y)=1$
${{x}^{2}}+{{y}^{2}}-2xy+x-y=1$ …. (2)
Persamaan (1) dikurang dengan persamaan (2), diperoleh:
$4xy-2x=0$
$2x(2y-1)=0$
$x=0$ atau $y=\frac{1}{2}$
$x=0\Rightarrow y=\frac{1\pm \sqrt{5}}{2}\Rightarrow x+y=\frac{1}{2}\pm \frac{1}{2}\sqrt{5}$
$y=\frac{1}{2}\Rightarrow x=\pm \frac{1}{2}\sqrt{5}\Rightarrow x+y=\frac{1}{2}\pm \frac{1}{2}\sqrt{5}$
Jadi, pernyataan (1) dan (3) BENAR, maka opsi B
Jawaban: B
Matematika Dasar SIMAK UI 2012 No. 19
Jika persamaan matriks ${{D}^{-1}}.{{B}^{-1}}-{{D}^{-1}}.{{C}^{-1}}=A$, $A\ne 0$, maka pernyataan tersebut setara dengan …
(1) BD = CD
(2) B = C
(3) ABD = ACD
(4) ${{B}^{-1}}-{{C}^{-1}}=DA$
Pembahasan:
${{D}^{-1}}.{{B}^{-1}}-{{D}^{-1}}.{{C}^{-1}}=A$
$D({{D}^{-1}}.{{B}^{-1}}-{{D}^{-1}}.{{C}^{-1}})=D.A$
${{B}^{-1}}-{{C}^{-1}}=D.A$
Jawaban: D
Matematika Dasar SIMAK UI 2012 No. 20
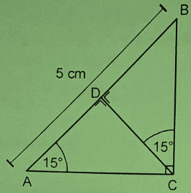
Pada segitiga siku-siku ABC dengan siku-siku di C, besar $\angle A={{15}^{o}}$ dan panjang sisi AB = 5 cm. Titik D pada sisi AB sedemikian sehingga CD tegak lurus AB dan $\angle BCD=\angle A$. Pernyataan berikut ini yang benar adalah …
(1) $AD=5{{\sin }^{2}}{{15}^{o}}$
(2) $CD=5\sin {{15}^{o}}\cos {{15}^{o}}$
(3) AD < CD
(4) BD < AD
Pembahasan:
Perhatikan gambar berikut:
*) AC = $5\cos {{15}^{o}}$
*) BC = $5\sin {{15}^{o}}$
*) CD = AC.$\sin {{15}^{o}}$, maka:
CD = $5\sin {{15}^{o}}.\cos {{15}^{o}}$ (BENAR)
*) AD = AC.$\cos {{15}^{o}}$
AD = 5.${{\cos }^{2}}{{15}^{o}}$
*) $AD
$\cos {{15}^{o}} < \sin {{15}^{o}}$ (SALAH)
*) BD < AD
$5-AD < AD$
$5-5{{\cos }^{2}}{{15}^{o}} < 5{{\cos }^{2}}{{15}^{o}}$
$5(1-{{\cos }^{2}}{{15}^{o}}) < 5{{\cos }^{2}}{{15}^{o}}$
$si{{n}^{2}}{{15}^{o}} < {{\cos }^{2}}{{15}^{o}}$ (BENAR)
Jawaban: C
Artikel Terkait:
|






Post a Comment for "Pembahasan Soal SIMAK UI 2012 Matematika Dasar Kode 223"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.