Pembahasan Matematika Dasar SNMPTN/SBMPTN 2012
Semangat pagi, semua! saya berharap semua masih tetap fokus untuk meraih impian menjadi sukses, masuk Perguruan Tinggi Negeri (PTN) yang diidam-idamkan. Coba bayangkan, jika kalian ingin mencapai suatu tempat di seberang sungaitentu harus melakukan suatu usaha untuk bisa berada di seberang dan dalam melakukan usaha tersebut dibutuhkan kemampuan berpikir beberapa pemikiran yang mungkin adalah berenang, melihat sekelilingnya apakah ada pohon pisang atau bambu yang dapat dijadikan sebuah rakit. Begitu jugalah untuk bisa menjadi pemenang PTN kalian harus melakukan usaha dan konsisten. Konsisten? Ya, harus konsisten, seperti ilustrasi tadi, coba kalau kalian berenangnya tidak konsisten, berhenti ditengah sungai, apa yang terjadi? tentu, tenggelam bukan? terbawa arus yang tak jelas. Jadi, adik-adik tetap fokus dan konsisten belajarnya ya....! Semangat!!! nih b4ngrp aja tetap semangat share soal dan pembahasan supaya kalian bisa belajar. seperti biasa... masih ingat aturan belajarnya? Download terlebih dahulu soalnya, jawab sendiri kemudian bolehlah diintip pembahasan ini.
Matematika Dasar SBMPTN 2012 No. 1
Jika $a$ dan $b$ adalah bilangan bulat positif yang memenuhi ${{a}^{b}}={{2}^{20}}-{{2}^{19}}$, maka nilai $a+b$ adalah …
A. 3 B. 7 C. 19 D. 21 E. 23
Pembahasan:
${{a}^{b}}={{2}^{20}}-{{2}^{19}}$
${{a}^{b}}={{2}^{19}}(2-1)$
${{a}^{b}}={{2}^{19}}\Leftrightarrow a=2;b=19$
$a+b=2+19=21$
Jawaban: D
Matematika Dasar SBMPTN 2012 No. 2
Nilai minimum fungsi objektif (tujuan) $f(x,y)=3x+4y$ dengan kendala $x+y\ge 20$, $x\ge 5$, dan $y\ge 5$ adalah …
A. 75 B. 65 C. 60 D. 55 E. 50
Pembahasan:

$A(15,5)\Rightarrow f(15,5)=3.15+4.5=65$
$A(5,15)\Rightarrow f(5,15)=3.5+4.15=75$
Jadi, nilai minimum adalah 65.
Jawaban: B
Matematika Dasar SBMPTN 2012 No. 3
Jika $p+1$ dan $p-1$ adalah akar-akar pesamaan ${{x}^{2}}-4x+a=0$, maka nilai $a$ adalah …
A. 0 B. 1 C. 2 D. 3 E. 4
Pembahasan:
${{x}^{2}}-4x+a=0$ akar-akarnya adalah $p+1$ dan $p-1$, maka:
$(p+1)+(p-1)=\frac{-(-4)}{1}$
$2p=4\Leftrightarrow p=2$
$(p+1).(p-1)=\frac{a}{1}$
$(2+1).(2-1)=a\Leftrightarrow a=3$
Jawaban: D
Matematika Dasar SBMPTN 2012 No. 4
Rata-rata nilai tes matematika 10 siswa adalah 65. Jika ditambah 5 nilai siswa lainnya maka rata-ratanya menjadi 70. Nilai rata-rata 5 siswa yang ditambahkan tersebut adalah …
A. 75 B. 78 C. 80 D. 82 E. 85
Pembahasan:
${{n}_{1}}=10$ dan ${{\bar{x}}_{1}}=65$
${{n}_{2}}=5$ dan ${{\bar{x}}_{total}}=70$
${{\bar{x}}_{2}}=...$
${{\bar{x}}_{total}}=\frac{{{n}_{1}}.{{{\bar{x}}}_{1}}+{{n}_{2}}.{{{\bar{x}}}_{2}}}{{{n}_{1}}+{{n}_{2}}}$
$70=\frac{10.65+5.{{{\bar{x}}}_{2}}}{10+5}$
$1050=650+5{{\bar{x}}_{2}}$
$400=5{{\bar{x}}_{2}}\Leftrightarrow {{\bar{x}}_{2}}=80$
Jawaban: C
Matematika Dasar SBMPTN 2012 No. 5
Jika $x+2y+z=2$, $2x+y=4$, dan $y+2z=1$, maka nilai $x-2y-3z$ adalah …
A. -4 B. -2 C. 0 D. 1 E. 2
Pembahasan:
$2x+y=4$
$x+2y+z=2$
----------------- (-)
$x-y-z=2$
$y+2z=1$
----------------- (-)
$x-2y-3z=1$
Jawaban: D
Matematika Dasar SBMPTN 2012 No. 6
Jika $f(x)=2x+5$, $g(x)=ax+4$, dan $g(f(1))=25$, maka nilai $g(1)$ adalah …
A. 1 B. 3 C. 5 D. 6 E. 7
Pembahasan:
$f(x)=2x+5\Rightarrow f(1)=2.1+5=7$
$g(f(1))=25$
$g(7)=25$
$g(7)=7a+4=25\Rightarrow a=3$
$g(x)=3x+4\Rightarrow g(1)=3.1+4=7$
Jawaban: E
Matematika Dasar SBMPTN 2012 No. 7
Jika diagram batang di bawah ini memperlihatkan frekuensi kumulatif hasil tes matematika siswa kelas XII, maka persentase siswa yang memperoleh nilai 8 adalah …
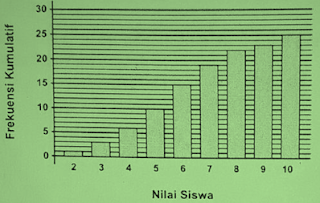
A. 12% B. 15% C. 20% D. 22% E. 80%
Pembahasan:

Persentase nilai 8:
$=\frac{3}{25}\times 100%=12%$
Jawaban: A
Matematika Dasar SBMPTN 2012 No. 8
Jika $f$ adalah fungsi kuadrat yang grafiknya melalui titik $(1,0)$, $(3,0)$, dan $(0,3)$, maka nilai $f(8)$ adalah …
A. 7 B. 14 C. 21 D. 28 E. 35
Pembahasan:
$(1,0)\Rightarrow {{x}_{1}}=1$
$(3,0)\Rightarrow {{x}_{2}}=3$
$f(x)=a(x-{{x}_{1}})(x-{{x}_{2}})$
$f(x)=a(x-1)(x-3)$
Melalui titik $(0,3)$, maka:
$3=a(0-1)(0-3)\Rightarrow a=1$
$f(8)=1.(8-1)(8-3)=35$
Jawaban: E
Matematika Dasar SBMPTN 2012 No. 9
Jika matriks $A=\left[ \begin{matrix} 2 & 3 \\ 1 & 0 \\ \end{matrix} \right]$, $B=\left[ \begin{matrix} 2 & 0 \\ 1 & 3 \\ \end{matrix} \right]$, dan $C=\left[ \begin{matrix} -5 & -6 \\ 2 & 8 \\ \end{matrix} \right]$, maka determinan matriks AB + C adalah …
A. 2 B. 3 C. 4 D. 5 E. 6
Pembahasan:
$AB+C=\left[ \begin{matrix} 2 & 3 \\ 1 & 0 \\ \end{matrix} \right].\left[ \begin{matrix} 2 & 0 \\ 1 & 3 \\ \end{matrix} \right]+\left[ \begin{matrix} -5 & -6 \\ 2 & 8 \\ \end{matrix} \right]$
$AB+C=\left[ \begin{matrix} 7 & 9 \\ 2 & 0 \\ \end{matrix} \right]+\left[ \begin{matrix} -5 & -6 \\ 2 & 8 \\ \end{matrix} \right]$
$AB+C=\left[ \begin{matrix} 2 & 3 \\ 4 & 8 \\ \end{matrix} \right]$
$\det (AB+C)=2.8-3.4=4$
Jawaban: C
Matematika Dasar SBMPTN 2012 No.10
Jika $a$ adalah suku pertama, $r$ adalah rasio, dan ${{S}_{n}}={{5}^{n+2}}-25$ adalah jumlah $n$ suku pertama deret geometri, maka nilai $a+r$ adalah …
A. 95 B. 105 C. 125 D. 225 E. 500
Pembahasan:
${{S}_{n}}={{5}^{n+2}}-25$
$a={{S}_{1}}={{5}^{1+2}}-25=100$
${{U}_{2}}={{S}_{2}}-{{S}_{1}}$
${{U}_{2}}=({{5}^{2+2}}-25)-100$
${{U}_{2}}=500$
$ar=500$
$100.r=500$
$r=5$
$a+r=100+5=105$
Jawaban: B
Matematika Dasar SBMPTN 2012 No. 11
Jika suatu persegi dengan panjang sisi satu satuan dibagi menjadi 5 persegi panjang dengan luas yang sama seperti ditunjukkan pada gambar, maka panjang ruas garis AB adalah …
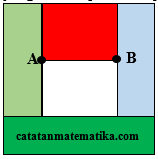
A. $\frac{1}{5}$ B. $\frac{1}{4}$ C. $\frac{2}{5}$ D. $\frac{1}{2}$ E. $\frac{3}{5}$
Pembahasan:

${{L}_{1}}=\frac{1}{5}\Rightarrow x=\frac{1}{5}$
${{L}_{2}}=(1-x).y=\frac{1}{5}$
$(1-\frac{1}{5}).y=\frac{1}{5}$
$\frac{4}{5}y=\frac{1}{5}\Leftrightarrow y=\frac{1}{4}$
$AB=1-2y=1-2.\frac{1}{4}=\frac{1}{2}$
Jawaban: D
Matematika Dasar SNMPTN/SBMPTN 2012 No. 12
Jika sebuah barang diberi potongan harga sebesar 20%, maka untuk mengembalikan ke harga semula harganya harus dinaikkan sebesar …
A. 10% B. 20% C. 25% D. 30% E. 40%
Pembahasan:
Misalkan harga barang = Rp. 100.000
Potongan harga 20% maka harganya menjadi Rp. 80.000
Agar harga kembali ke harga semula maka harga harus dinaikkan 20.000
Persentasenya adalah:
$=\frac{20.000}{80.000}$ x 100% =25%
Jawaban: C
Matematika Dasar SBMPTN 2012 No. 13
Semua nilai $x$ yang memenuhi $(x-3)(x+3)\ge (x+3)$ adalah …
A. $x\le -3$ atau $x\ge 4$
B. $-3\le x\le 4$
C. $-2\le x\le 4$
D. $x\ge -2$
E. $x\ge -4$
Pembahasan:
$(x-3)(x+3)\ge (x+3)$
${{x}^{2}}-9\ge x+3$
${{x}^{2}}-x-12\ge 0$
$(x-4)(x+3)\ge 0$
$x=4,x=-3$
$x\le -3$ atau $x\ge 4$
Jawaban: A
Matematika Dasar SBMPTN 2012 No. 14
Jika suatu barisan aritmetika mempunyai suku pertama sama dengan empat kali beda barisan tersebut dan jumlah empat suku pertamanya adalah 66, maka suku kelima barisan tersebut adalah …
A. 16 B. 18 C. 20 D. 22 E. 24
Pembahasan:
Barisan aritmetika:
$a=4b$
${{S}_{n}}=\frac{n}{2}(2a+(n-1)b)$
${{S}_{4}}=\frac{4}{2}(2a+3b)=66$
$2a+3b=33$
$2.4b+3b=33$
$11b=33\Rightarrow b=3;a=12$
${{U}_{5}}=a+4b=12+4.3=24$
Jawaban: E
Matematika Dasar SBMPTN 2012 No. 15
Jika ${}^{3}\log 5=x$ dan $^{2}\log 3=y$, maka nilai ${}^{3}\log 10$ adalah …
A. $\frac{xy+1}{y}$
B. $\frac{xy+1}{x}$
C. $\frac{xy}{y+1}$
D. $\frac{xy}{x+1}$
E. $\frac{xy+1}{y+1}$
Pembahasan:
$^{2}\log {{3.}^{3}}\log 5=y.x$
$^{2}\log 5=xy$
${}^{3}\log 10=\frac{{}^{2}\log 10}{{}^{2}\log 3}$
$=\frac{{}^{2}\log 5.2}{{}^{2}\log 3}$
$=\frac{{}^{2}\log 5+{}^{2}\log 2}{{}^{2}\log 3}$
$=\frac{xy+1}{y}$
Jawaban: A
Matematika Dasar SBMPTN 2012 No. 1
Jika $a$ dan $b$ adalah bilangan bulat positif yang memenuhi ${{a}^{b}}={{2}^{20}}-{{2}^{19}}$, maka nilai $a+b$ adalah …
A. 3 B. 7 C. 19 D. 21 E. 23
Pembahasan:
${{a}^{b}}={{2}^{20}}-{{2}^{19}}$
${{a}^{b}}={{2}^{19}}(2-1)$
${{a}^{b}}={{2}^{19}}\Leftrightarrow a=2;b=19$
$a+b=2+19=21$
Jawaban: D
Matematika Dasar SBMPTN 2012 No. 2
Nilai minimum fungsi objektif (tujuan) $f(x,y)=3x+4y$ dengan kendala $x+y\ge 20$, $x\ge 5$, dan $y\ge 5$ adalah …
A. 75 B. 65 C. 60 D. 55 E. 50
Pembahasan:

$A(15,5)\Rightarrow f(15,5)=3.15+4.5=65$
$A(5,15)\Rightarrow f(5,15)=3.5+4.15=75$
Jadi, nilai minimum adalah 65.
Jawaban: B
Matematika Dasar SBMPTN 2012 No. 3
Jika $p+1$ dan $p-1$ adalah akar-akar pesamaan ${{x}^{2}}-4x+a=0$, maka nilai $a$ adalah …
A. 0 B. 1 C. 2 D. 3 E. 4
Pembahasan:
${{x}^{2}}-4x+a=0$ akar-akarnya adalah $p+1$ dan $p-1$, maka:
$(p+1)+(p-1)=\frac{-(-4)}{1}$
$2p=4\Leftrightarrow p=2$
$(p+1).(p-1)=\frac{a}{1}$
$(2+1).(2-1)=a\Leftrightarrow a=3$
Jawaban: D
Matematika Dasar SBMPTN 2012 No. 4
Rata-rata nilai tes matematika 10 siswa adalah 65. Jika ditambah 5 nilai siswa lainnya maka rata-ratanya menjadi 70. Nilai rata-rata 5 siswa yang ditambahkan tersebut adalah …
A. 75 B. 78 C. 80 D. 82 E. 85
Pembahasan:
${{n}_{1}}=10$ dan ${{\bar{x}}_{1}}=65$
${{n}_{2}}=5$ dan ${{\bar{x}}_{total}}=70$
${{\bar{x}}_{2}}=...$
${{\bar{x}}_{total}}=\frac{{{n}_{1}}.{{{\bar{x}}}_{1}}+{{n}_{2}}.{{{\bar{x}}}_{2}}}{{{n}_{1}}+{{n}_{2}}}$
$70=\frac{10.65+5.{{{\bar{x}}}_{2}}}{10+5}$
$1050=650+5{{\bar{x}}_{2}}$
$400=5{{\bar{x}}_{2}}\Leftrightarrow {{\bar{x}}_{2}}=80$
Jawaban: C
Matematika Dasar SBMPTN 2012 No. 5
Jika $x+2y+z=2$, $2x+y=4$, dan $y+2z=1$, maka nilai $x-2y-3z$ adalah …
A. -4 B. -2 C. 0 D. 1 E. 2
Pembahasan:
$2x+y=4$
$x+2y+z=2$
----------------- (-)
$x-y-z=2$
$y+2z=1$
----------------- (-)
$x-2y-3z=1$
Jawaban: D
Matematika Dasar SBMPTN 2012 No. 6
Jika $f(x)=2x+5$, $g(x)=ax+4$, dan $g(f(1))=25$, maka nilai $g(1)$ adalah …
A. 1 B. 3 C. 5 D. 6 E. 7
Pembahasan:
$f(x)=2x+5\Rightarrow f(1)=2.1+5=7$
$g(f(1))=25$
$g(7)=25$
$g(7)=7a+4=25\Rightarrow a=3$
$g(x)=3x+4\Rightarrow g(1)=3.1+4=7$
Jawaban: E
Matematika Dasar SBMPTN 2012 No. 7
Jika diagram batang di bawah ini memperlihatkan frekuensi kumulatif hasil tes matematika siswa kelas XII, maka persentase siswa yang memperoleh nilai 8 adalah …

A. 12% B. 15% C. 20% D. 22% E. 80%
Pembahasan:

Persentase nilai 8:
$=\frac{3}{25}\times 100%=12%$
Jawaban: A
Matematika Dasar SBMPTN 2012 No. 8
Jika $f$ adalah fungsi kuadrat yang grafiknya melalui titik $(1,0)$, $(3,0)$, dan $(0,3)$, maka nilai $f(8)$ adalah …
A. 7 B. 14 C. 21 D. 28 E. 35
Pembahasan:
$(1,0)\Rightarrow {{x}_{1}}=1$
$(3,0)\Rightarrow {{x}_{2}}=3$
$f(x)=a(x-{{x}_{1}})(x-{{x}_{2}})$
$f(x)=a(x-1)(x-3)$
Melalui titik $(0,3)$, maka:
$3=a(0-1)(0-3)\Rightarrow a=1$
$f(8)=1.(8-1)(8-3)=35$
Jawaban: E
Matematika Dasar SBMPTN 2012 No. 9
Jika matriks $A=\left[ \begin{matrix} 2 & 3 \\ 1 & 0 \\ \end{matrix} \right]$, $B=\left[ \begin{matrix} 2 & 0 \\ 1 & 3 \\ \end{matrix} \right]$, dan $C=\left[ \begin{matrix} -5 & -6 \\ 2 & 8 \\ \end{matrix} \right]$, maka determinan matriks AB + C adalah …
A. 2 B. 3 C. 4 D. 5 E. 6
Pembahasan:
$AB+C=\left[ \begin{matrix} 2 & 3 \\ 1 & 0 \\ \end{matrix} \right].\left[ \begin{matrix} 2 & 0 \\ 1 & 3 \\ \end{matrix} \right]+\left[ \begin{matrix} -5 & -6 \\ 2 & 8 \\ \end{matrix} \right]$
$AB+C=\left[ \begin{matrix} 7 & 9 \\ 2 & 0 \\ \end{matrix} \right]+\left[ \begin{matrix} -5 & -6 \\ 2 & 8 \\ \end{matrix} \right]$
$AB+C=\left[ \begin{matrix} 2 & 3 \\ 4 & 8 \\ \end{matrix} \right]$
$\det (AB+C)=2.8-3.4=4$
Jawaban: C
Matematika Dasar SBMPTN 2012 No.10
Jika $a$ adalah suku pertama, $r$ adalah rasio, dan ${{S}_{n}}={{5}^{n+2}}-25$ adalah jumlah $n$ suku pertama deret geometri, maka nilai $a+r$ adalah …
A. 95 B. 105 C. 125 D. 225 E. 500
Pembahasan:
${{S}_{n}}={{5}^{n+2}}-25$
$a={{S}_{1}}={{5}^{1+2}}-25=100$
${{U}_{2}}={{S}_{2}}-{{S}_{1}}$
${{U}_{2}}=({{5}^{2+2}}-25)-100$
${{U}_{2}}=500$
$ar=500$
$100.r=500$
$r=5$
$a+r=100+5=105$
Jawaban: B
Matematika Dasar SBMPTN 2012 No. 11
Jika suatu persegi dengan panjang sisi satu satuan dibagi menjadi 5 persegi panjang dengan luas yang sama seperti ditunjukkan pada gambar, maka panjang ruas garis AB adalah …

A. $\frac{1}{5}$ B. $\frac{1}{4}$ C. $\frac{2}{5}$ D. $\frac{1}{2}$ E. $\frac{3}{5}$
Pembahasan:

${{L}_{1}}=\frac{1}{5}\Rightarrow x=\frac{1}{5}$
${{L}_{2}}=(1-x).y=\frac{1}{5}$
$(1-\frac{1}{5}).y=\frac{1}{5}$
$\frac{4}{5}y=\frac{1}{5}\Leftrightarrow y=\frac{1}{4}$
$AB=1-2y=1-2.\frac{1}{4}=\frac{1}{2}$
Jawaban: D
Matematika Dasar SNMPTN/SBMPTN 2012 No. 12
Jika sebuah barang diberi potongan harga sebesar 20%, maka untuk mengembalikan ke harga semula harganya harus dinaikkan sebesar …
A. 10% B. 20% C. 25% D. 30% E. 40%
Pembahasan:
Misalkan harga barang = Rp. 100.000
Potongan harga 20% maka harganya menjadi Rp. 80.000
Agar harga kembali ke harga semula maka harga harus dinaikkan 20.000
Persentasenya adalah:
$=\frac{20.000}{80.000}$ x 100% =25%
Jawaban: C
Matematika Dasar SBMPTN 2012 No. 13
Semua nilai $x$ yang memenuhi $(x-3)(x+3)\ge (x+3)$ adalah …
A. $x\le -3$ atau $x\ge 4$
B. $-3\le x\le 4$
C. $-2\le x\le 4$
D. $x\ge -2$
E. $x\ge -4$
Pembahasan:
$(x-3)(x+3)\ge (x+3)$
${{x}^{2}}-9\ge x+3$
${{x}^{2}}-x-12\ge 0$
$(x-4)(x+3)\ge 0$
$x=4,x=-3$
$x\le -3$ atau $x\ge 4$
Jawaban: A
Matematika Dasar SBMPTN 2012 No. 14
Jika suatu barisan aritmetika mempunyai suku pertama sama dengan empat kali beda barisan tersebut dan jumlah empat suku pertamanya adalah 66, maka suku kelima barisan tersebut adalah …
A. 16 B. 18 C. 20 D. 22 E. 24
Pembahasan:
Barisan aritmetika:
$a=4b$
${{S}_{n}}=\frac{n}{2}(2a+(n-1)b)$
${{S}_{4}}=\frac{4}{2}(2a+3b)=66$
$2a+3b=33$
$2.4b+3b=33$
$11b=33\Rightarrow b=3;a=12$
${{U}_{5}}=a+4b=12+4.3=24$
Jawaban: E
Matematika Dasar SBMPTN 2012 No. 15
Jika ${}^{3}\log 5=x$ dan $^{2}\log 3=y$, maka nilai ${}^{3}\log 10$ adalah …
A. $\frac{xy+1}{y}$
B. $\frac{xy+1}{x}$
C. $\frac{xy}{y+1}$
D. $\frac{xy}{x+1}$
E. $\frac{xy+1}{y+1}$
Pembahasan:
$^{2}\log {{3.}^{3}}\log 5=y.x$
$^{2}\log 5=xy$
${}^{3}\log 10=\frac{{}^{2}\log 10}{{}^{2}\log 3}$
$=\frac{{}^{2}\log 5.2}{{}^{2}\log 3}$
$=\frac{{}^{2}\log 5+{}^{2}\log 2}{{}^{2}\log 3}$
$=\frac{xy+1}{y}$
Jawaban: A
Artikel Terkait:
|

Post a Comment for "Pembahasan Matematika Dasar SNMPTN/SBMPTN 2012"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.