Pembahasan SBMPTN 2011 Matematika IPA
Postingan kali ini adalah Pembahasan Matematika IPA SNMPTN 2011 Kode 591. Di dalam postingan ini juga saya memberikan file soal dalam bentuk pdf yang dapat kalian unduh.
Matematika IPA SBMPTN 2011 No. 1
Diketahui vektor $\vec{u}=(a,-2,-1)$ dan $\vec{v}=(a,a,-1)$. Jika vektor $\vec{u}$ tegak lurus pada $\vec{v}$, maka nilai $a$ adalah …
A. -1
B. 0
C. 1
D. 2
E. 3
Pembahasan:
Jika $\vec{u}\bot \vec{v}$ maka:
$\vec{u}.\vec{v}=0$
$\left( \begin{matrix} a \\ -2 \\ -1 \\ \end{matrix} \right).\left( \begin{matrix} a \\ a \\ -1 \\ \end{matrix} \right)=0$
${{a}^{2}}-2a+1=0$
$(a-1)(a-1)=0$
$a=1$
Jawaban: C
Matematika IPA SBMPTN 2011 No. 2
Pernyataan berikut yang benar adalah …
A. Jika sin x = sin y, maka x = y
B. Untuk setiap vektor $\vec{u}$, $\vec{v}$, dan $\vec{w}$ berlaku $\vec{u}.(\vec{v}.\vec{w})=(\vec{u}.\vec{v}).\vec{w}$
C. Jika $\int\limits_{a}^{b}{f(x)dx}=0$ maka $f(x)=0$
D. Ada fungsi $f$ sehingga $\underset{x\to 0}{\mathop{\lim }}\,f(x)\ne f(c)$ untuk suatu c.
E. $1-\cos 2x=2{{\cos }^{2}}x$
Pembahasan:
A salah, contoh: $\sin {{30}^{o}}=\sin {{150}^{o}}$, ${{30}^{o}}\ne {{150}^{o}}$
B salah, $\vec{u}.(\vec{v}.\vec{w})\ne (\vec{u}.\vec{v}).\vec{w}$
C salah, $\int\limits_{a}^{b}{f(x)dx}=F(b)-F(a)$, jadi $f(x)$ tidak selalu nol.
D benar, karena walaupun f(x) jika dimasukkan c hasilnya menjadi $\infty $, apabila kita kerjakan dengan limit bisa jadi hasilnya bilangan real.
E salah,
$1-\cos 2x=1-(2{{\cos }^{2}}x-1)$
$1-\cos 2x=2-2{{\cos }^{2}}x$
Jawaban: D
Matematika IPA SBMPTN 2011 No. 3
Luas daerah di bawah $y=-{{x}^{2}}+8x$, di atas $y=6x-24$, dan terletak di kuadran I adalah …
A. $\int\limits_{0}^{4}{(-{{x}^{2}}+8x)dx}+\int\limits_{4}^{6}{({{x}^{2}}-2x-24)dx}$
B. $\int\limits_{0}^{4}{(-{{x}^{2}}+8x)dx}+\int\limits_{4}^{6}{(-{{x}^{2}}+2x+24)dx}$
C. $\int\limits_{0}^{6}{(-{{x}^{2}}+8x)dx}+\int\limits_{6}^{8}{(-{{x}^{2}}+2x+24)dx}$
D. $\int\limits_{4}^{6}{(6x-24)dx}+\int\limits_{6}^{8}{(-{{x}^{2}}+8x)dx}$
E. $\int\limits_{0}^{4}{(6x-24)dx}+\int\limits_{4}^{6}{(-{{x}^{2}}+8x)dx}$
Pembahasan:
Perhatikan gambar berikut ini!
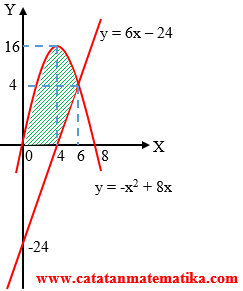
Luas yang diarsir:
= $\int\limits_{0}^{4}{(-{{x}^{2}}+8x)dx}$ + $\int\limits_{4}^{6}{((-{{x}^{2}}+8x)-(6x-24))dx}$
= $\int\limits_{0}^{4}{(-{{x}^{2}}+8x)dx}+\int\limits_{4}^{6}{(-{{x}^{2}}+2x+24)dx}$
Jawaban: B
Matematika IPA SBMPTN 2011 No. 4
Jika $\sin x+\cos x=-\frac{1}{5}$ dan $\frac{3\pi }{4}\le x < \pi $, maka nilai $\sin 2x$ adalah …
A. $\frac{-24}{25}$
B. $\frac{-7}{25}$
C. $\frac{7}{25}$
D. $\frac{8}{25}$
E. $\frac{24}{25}$
Pembahasan:
$\sin x+\cos x=-\frac{1}{5}$
Kuadratkan kedua ruas
${{\left( \sin x+\cos x \right)}^{2}}={{\left( -\frac{1}{5} \right)}^{2}}$
${{\sin }^{2}}x+2\sin x.\cos x+{{\cos }^{2}}x=\frac{1}{25}$
${{\sin }^{2}}x+{{\cos }^{2}}x+2\sin x.\cos x=\frac{1}{25}$
$1+\sin 2x=\frac{1}{25}$
$\sin 2x=\frac{1}{25}-1=\frac{-24}{25}$
Jawaban: A
Matematika IPA SBMPTN 2011 No. 5
Kedua akar suku banyak $S(x)={{x}^{2}}-63x+c$ merupakan bilangan prima. Banyak nilai $c$ yang mungkin adalah ….
A. 0
B. 1
C. 2
D. 3
E. lebih dari 3
Pembahasan:
$S(x)={{x}^{2}}-63x+c$, akar-akarnya ${{x}_{1}}$ dan ${{x}_{2}}$ maka:
${{x}_{1}}+{{x}_{2}}=63$ karena ${{x}_{1}}$ dan ${{x}_{2}}$ bilangan prima, maka yang memungkinkan adalah ${{x}_{1}}=2$ dan ${{x}_{2}}=61$.
${{x}_{1}}.{{x}_{2}}=c\Leftrightarrow c=2.61=122$.
Banyak nilai $c$ yang memungkinkan adalah 1.
Jawaban: B
Matematika IPA SBMPTN 2011 No. 6
Diketahui segilima ABCDE, dengan $A(0,2)$, $B(4,0)$, $C(2\pi +1,0)$, $D(2\pi +1,4)$, dan $E(0,4)$. Titik P dipilih secara acak dari titik di dalam segilima tersebut. Peluang sudut APB berukuran tumpul adalah …
A. $\frac{3}{8}$
B. $\frac{1}{4}$
C. $\frac{1}{2}$
D. $\frac{5}{16}$
E. $\frac{5}{8}$
Pembahasan:
Perhatikan gambar berikut ini!
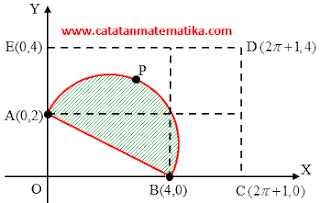
$AB=\sqrt{{{4}^{2}}+{{2}^{2}}}=2\sqrt{5}$
${{L}_{1}}$ = Luas setengah lingkaran dengan diameter AB
${{L}_{1}}=\frac{1}{2}.\frac{1}{4}\pi {{d}^{2}}$
$=\frac{1}{8}\pi {{(2\sqrt{5})}^{2}}$
${{L}_{1}}=\frac{5}{2}\pi $
${{L}_{2}}$ = Luas daerah ABCDE
= Luas OCDE – Luas OAB
$=4(2\pi +1)-\frac{1}{2}.4.2$
${{L}_{2}}$ $=8\pi $
Peluang sudut APB tumbul adalah:
$=\frac{{{L}_{1}}}{{{L}_{2}}}=\frac{\frac{5}{2}\pi }{8\pi }=\frac{5}{16}$
Jawaban: D
Matematika IPA SBMPTN 2011 No. 7
Diketahui limas T.ABC dengan TA tegak lurus bidang ABC. Panjang rusuk AB, AC, BC dan TA berturut-turut adalah 3 cm, 4 cm, 5 cm, dan$\frac{9}{5}$ cm. Jika $\varphi $ sudut antara bidang BCT dengan bidang ABC, maka nilai $\cos \varphi $ adalah …
A. $\frac{4}{5}$
B. $\frac{3}{5}$
C. $\frac{6}{25}$
D. $\frac{9}{25}$
E. $\frac{12}{25}$
Pembahasan:
Perhatikan gambar berikut!
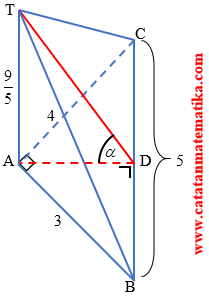
Luas segitiga ABC:
$\frac{1}{2}.AD.BC=\frac{1}{2}.AB.AC$
$AD=\frac{AB.AC}{BC}$
$AD=\frac{3.4}{5}=\frac{12}{5}$
Perhatikan segitiga TAD siku-siku di A, maka:
$TD=\sqrt{A{{D}^{2}}+A{{T}^{2}}}$
$TD=\sqrt{{{\left( \frac{12}{5} \right)}^{2}}+{{\left( \frac{9}{5} \right)}^{2}}}=\frac{15}{5}$
$\cos \alpha =\frac{AE}{TE}=\frac{\frac{12}{5}}{\frac{15}{5}}=\frac{12}{15}=\frac{4}{5}$
Jawaban: A
Matematika IPA SBMPTN 2011 No. 8
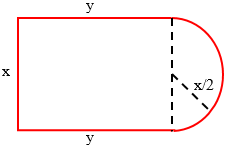
Kolam renang berbentuk gabungan persegi panjang dan setengah lingkaran seperti gambar di atas. Keliling kolam renang sama dengan $a$ satuan panjang. Agar luas kolam renang maksimum, maka $x$ = … satuan panjang.
A. $\frac{2a}{\pi }$
B. $\frac{a}{\pi }$
C. $\frac{a}{4+\pi }$
D. $\frac{a}{4+2\pi }$
E. $\frac{2a}{4+\pi }$
Pembahasan:
Keliling = $a$
$x+2y+\frac{1}{2}\pi x=a$
$\left( 1+\frac{1}{2}\pi \right)x+2y=a$
$2y=a-\left( 1+\frac{1}{2}\pi \right)x$
$y=\frac{1}{2}a-\left( \frac{1}{2}+\frac{1}{4}\pi \right)x$
Luas = Luas persegi panjang + Luas setengah lingkaran
$L=x.y+\frac{1}{2}.\frac{1}{4}\pi {{x}^{2}}$
$L=x\left( \frac{1}{2}a-\left( \frac{1}{2}+\frac{1}{4}\pi \right)x \right)+\frac{1}{8}\pi {{x}^{2}}$
$L=\frac{1}{2}ax-\left( \frac{1}{2}+\frac{1}{4}\pi \right){{x}^{2}}+\frac{1}{8}\pi {{x}^{2}}$
$L=\frac{1}{2}ax+\left( -\frac{1}{2}-\frac{1}{4}\pi +\frac{1}{8}\pi \right){{x}^{2}}$
$L=\frac{1}{2}ax+\left( -\frac{1}{2}-\frac{1}{8}\pi \right){{x}^{2}}$
Agar luas maksimum, maka L’ = 0
$\frac{1}{2}a+\left( -1-\frac{1}{4}\pi \right)x=0$
$\frac{1}{2}a=\left( \frac{4+\pi }{4} \right)x$
$2a=\left( 4+\pi \right)x$
$x=\frac{2a}{4+\pi }$
Jawaban: E
Matematika IPA SBMPTN 2011 No. 9
Diberikan $f(x)=a+bx$ dan $F(x)$ adalah anti turunan $f(x)$. Jika $F(1)-F(0)=3$ maka $2a+b$ adalah …
A. 10
B. 6
C. 5
D. 4
E. 3
Pembahasan:
$f(x)=a+bx$
$\int\limits_{0}^{1}{f(x)}dx=F(1)-F(0)$
$\int\limits_{0}^{1}{(a+bx)}dx=3$
$(\left. ax+\frac{1}{2}b{{x}^{2}}) \right|_{0}^{1}=3$
$(a.1+\frac{1}{2}b{{.1}^{2}})-(a.0+\frac{1}{2}b{{.0}^{2}})=3$
$a+\frac{1}{2}b=3$ } kedua ruas dikali 2
$2a+b=6$
Jawaban: B
Matematika IPA SBMPTN 2011 No. 10
Jika $\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{x}=\frac{1}{2}$, maka nilai $\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{\sqrt{1-x}-1}$ adalah …
A. -4
B. -2
C. -1
D. 2
E. 4
Pembahasan:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{\sqrt{1-x}-1}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{\sqrt{1-x}-1}\times \frac{\sqrt{1-x}+1}{\sqrt{1-x}+1}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)(\sqrt{1-x}+1)}{(1-x)-1}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{-x}\times (\sqrt{1-x}+1)$
$=-\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{x}\times (\sqrt{1-x}+1)$
$=-\frac{1}{2}\times (\sqrt{1-0}+1)$
$=-1$
Jawaban: C
Matematika IPA SBMPTN 2011 No. 11
$\cos {{35}^{o}}.\cos {{20}^{o}}-\sin {{35}^{o}}.\sin {{20}^{o}}$ = …
A. $\sin {{35}^{o}}$
B. $\sin {{55}^{o}}$
C. $\cos {{35}^{o}}$
D. $\cos {{15}^{o}}$
E. $\sin {{15}^{o}}$
Pembahasan:
$\cos {{35}^{o}}.\cos {{20}^{o}}-\sin {{35}^{o}}.\sin {{20}^{o}}$
$=\cos ({{35}^{o}}+{{20}^{o}})$
$=\cos {{55}^{o}}$
$=\cos ({{90}^{o}}-{{35}^{o}})$
$=\sin {{35}^{o}}$
Jawaban: A
Matematika IPA SBMPTN 2011 No. 12
Banyak siswa laki-laki 10 orang dan siswa perempuan 5 orang. Banyaknya cara untuk membentuk panitia yang beranggotakan 10 orang dan terdiri atas paling sedikit 2 orang perempuan dan paling banyak 4 orang perempuan adalah …
A. 4800
B. 3150
C. 2700
D. 2300
E. 2250
Pembahasan:
Kemungkinan-kemungkinannya adalah:
2 perempuan dan 8 laki-laki
$=C_{2}^{5}\times C_{8}^{10}=\frac{5!}{2!.3!}\times \frac{10!}{8!.2!}=450$
3 perempuan dan 7 laki-laki
$=C_{3}^{5}\times C_{7}^{10}=\frac{5!}{3!.2!}\times \frac{10!}{7!.3!}=1200$
4 perempuan dan 6 laki-laki
$=C_{4}^{5}\times C_{6}^{10}=\frac{5!}{4!.1!}\times \frac{10!}{6!.4!}=1050$
Seluruhnya = 450 + 1200 + 1050 = 2700
Jawaban: C
Matematika IPA SBMPTN 2011 No. 13
Diketahui $\vec{u}={{p}^{2}}\vec{i}+3\vec{j}-\vec{k}$ dan $\vec{v}=p\vec{i}+p\vec{j}-5\vec{k}$ dengan $-2 < p < 2$. Nilai maksimum $\vec{u}.\vec{v}$ adalah …
A. 8
B. 7
C. 5
D. 4
E. 3
Pembahasan:
$\vec{u}={{p}^{2}}\vec{i}+3\vec{j}-\vec{k}$ dan $\vec{v}=p\vec{i}+p\vec{j}-5\vec{k}$
$\vec{u}.\vec{v}=\left( \begin{matrix} {{p}^{2}} \\ 3 \\ -1 \\ \end{matrix} \right).\left( \begin{matrix} p \\ p \\ -5 \\ \end{matrix} \right)$
$\vec{u}.\vec{v}=-{{p}^{3}}+3p+5$
Agar maksimum maka $(\vec{u}.\vec{v})'=0$, maka:
$-3{{p}^{2}}+3=0$
${{p}^{2}}-1=0$
$(p+1)(p-1)=0$
$p=-1\vee p=1$
Substitusi ke: $\vec{u}.\vec{v}=-{{p}^{3}}+3p+5$
$p=-1\to \vec{u}.\vec{v}=-{{(-1)}^{3}}+3(-1)+5=3$
$p=1\to \vec{u}.\vec{v}=-{{1}^{3}}+3.1+5=7$
Jadi, nilai maksimum $\vec{u}.\vec{v}$ adalah 7.
Jawaban: B
Matematika IPA SBMPTN 2011 No. 14
Persamaan lingkaran dengan pusat $(2,3)$ dan menyinggung garis $y=2x$ adalah …
A. $5{{x}^{2}}+5{{y}^{2}}-20x-30y+12=0$
B. $5{{x}^{2}}+5{{y}^{2}}-20x-30y+49=0$
C. $5{{x}^{2}}+5{{y}^{2}}-20x-30y+54=0$
D. $5{{x}^{2}}+5{{y}^{2}}-20x-30y+60=0$
E. $5{{x}^{2}}+5{{y}^{2}}-20x-30y+64=0$
Pembahasan:
$y=2x\Leftrightarrow 2x-y=0$
$r$ = Jarak titik pusat $(2,3)$ ke garis $2x-y=0$
$r=\left| \frac{2{{x}_{1}}-{{y}_{1}}}{\sqrt{{{2}^{2}}+{{(-1)}^{2}}}} \right|$
$r=\left| \frac{2.2-3}{\sqrt{4+1}} \right|$
$r=\frac{1}{\sqrt{5}}$
Persamaan garis singgung lingkaran dengan pusat $(2,3)$ dan jari-jari $r=\frac{1}{\sqrt{5}}$ adalah:
${{(x-2)}^{2}}+{{(y-3)}^{2}}={{\left( \frac{1}{\sqrt{5}} \right)}^{2}}$
${{x}^{2}}-4x+4+{{y}^{2}}-6y+9=\frac{1}{5}$
$5{{x}^{2}}-20x+20+5{{y}^{2}}-30y+45=1$
$5{{x}^{2}}+5{{y}^{2}}-20x-30y+64=0$
Jawaban: E
Matematika IPA SBMPTN 2011 No. 15
Parabola $y=a{{x}^{2}}+bx+c$ puncaknya $(p,q)$, dicerminkan terhadap garis $y=q$ menghasilkan parabola $y=k{{x}^{2}}+lx+m$. Nilai $a+b+c+k+l+m$ adalah …
A. q
B. 2p
C. p
D. 2q
E. p + q
Pembahasan:
$(x,y)$ dicerminkan terhadap garis $y=q$ bayangannya $(x,2q-y)=(x',y')$, maka substitusikan $x=x'$ dan $y=2q-y'$ ke $y=a{{x}^{2}}+bx+c$, diperoleh:
$2q-y'=a{{(x')}^{2}}+b.x'+c$
$y=-a{{x}^{2}}-bx+2q-c$
$k{{x}^{2}}+lx+m\equiv -a{{x}^{2}}-bx+2q-c$
$k=-a$, $l=-b$, $m=2q-c$
Jadi, nilai
$a+b+c+k+l+m$
$=a+b+c-a-b+2q-c=2q$
$=2q$
Jawaban: D
Matematika IPA SBMPTN 2011 No. 1
Diketahui vektor $\vec{u}=(a,-2,-1)$ dan $\vec{v}=(a,a,-1)$. Jika vektor $\vec{u}$ tegak lurus pada $\vec{v}$, maka nilai $a$ adalah …
A. -1
B. 0
C. 1
D. 2
E. 3
Pembahasan:
Jika $\vec{u}\bot \vec{v}$ maka:
$\vec{u}.\vec{v}=0$
$\left( \begin{matrix} a \\ -2 \\ -1 \\ \end{matrix} \right).\left( \begin{matrix} a \\ a \\ -1 \\ \end{matrix} \right)=0$
${{a}^{2}}-2a+1=0$
$(a-1)(a-1)=0$
$a=1$
Jawaban: C
Matematika IPA SBMPTN 2011 No. 2
Pernyataan berikut yang benar adalah …
A. Jika sin x = sin y, maka x = y
B. Untuk setiap vektor $\vec{u}$, $\vec{v}$, dan $\vec{w}$ berlaku $\vec{u}.(\vec{v}.\vec{w})=(\vec{u}.\vec{v}).\vec{w}$
C. Jika $\int\limits_{a}^{b}{f(x)dx}=0$ maka $f(x)=0$
D. Ada fungsi $f$ sehingga $\underset{x\to 0}{\mathop{\lim }}\,f(x)\ne f(c)$ untuk suatu c.
E. $1-\cos 2x=2{{\cos }^{2}}x$
Pembahasan:
A salah, contoh: $\sin {{30}^{o}}=\sin {{150}^{o}}$, ${{30}^{o}}\ne {{150}^{o}}$
B salah, $\vec{u}.(\vec{v}.\vec{w})\ne (\vec{u}.\vec{v}).\vec{w}$
C salah, $\int\limits_{a}^{b}{f(x)dx}=F(b)-F(a)$, jadi $f(x)$ tidak selalu nol.
D benar, karena walaupun f(x) jika dimasukkan c hasilnya menjadi $\infty $, apabila kita kerjakan dengan limit bisa jadi hasilnya bilangan real.
E salah,
$1-\cos 2x=1-(2{{\cos }^{2}}x-1)$
$1-\cos 2x=2-2{{\cos }^{2}}x$
Jawaban: D
Matematika IPA SBMPTN 2011 No. 3
Luas daerah di bawah $y=-{{x}^{2}}+8x$, di atas $y=6x-24$, dan terletak di kuadran I adalah …
A. $\int\limits_{0}^{4}{(-{{x}^{2}}+8x)dx}+\int\limits_{4}^{6}{({{x}^{2}}-2x-24)dx}$
B. $\int\limits_{0}^{4}{(-{{x}^{2}}+8x)dx}+\int\limits_{4}^{6}{(-{{x}^{2}}+2x+24)dx}$
C. $\int\limits_{0}^{6}{(-{{x}^{2}}+8x)dx}+\int\limits_{6}^{8}{(-{{x}^{2}}+2x+24)dx}$
D. $\int\limits_{4}^{6}{(6x-24)dx}+\int\limits_{6}^{8}{(-{{x}^{2}}+8x)dx}$
E. $\int\limits_{0}^{4}{(6x-24)dx}+\int\limits_{4}^{6}{(-{{x}^{2}}+8x)dx}$
Pembahasan:
Perhatikan gambar berikut ini!

Luas yang diarsir:
= $\int\limits_{0}^{4}{(-{{x}^{2}}+8x)dx}$ + $\int\limits_{4}^{6}{((-{{x}^{2}}+8x)-(6x-24))dx}$
= $\int\limits_{0}^{4}{(-{{x}^{2}}+8x)dx}+\int\limits_{4}^{6}{(-{{x}^{2}}+2x+24)dx}$
Jawaban: B
Matematika IPA SBMPTN 2011 No. 4
Jika $\sin x+\cos x=-\frac{1}{5}$ dan $\frac{3\pi }{4}\le x < \pi $, maka nilai $\sin 2x$ adalah …
A. $\frac{-24}{25}$
B. $\frac{-7}{25}$
C. $\frac{7}{25}$
D. $\frac{8}{25}$
E. $\frac{24}{25}$
Pembahasan:
$\sin x+\cos x=-\frac{1}{5}$
Kuadratkan kedua ruas
${{\left( \sin x+\cos x \right)}^{2}}={{\left( -\frac{1}{5} \right)}^{2}}$
${{\sin }^{2}}x+2\sin x.\cos x+{{\cos }^{2}}x=\frac{1}{25}$
${{\sin }^{2}}x+{{\cos }^{2}}x+2\sin x.\cos x=\frac{1}{25}$
$1+\sin 2x=\frac{1}{25}$
$\sin 2x=\frac{1}{25}-1=\frac{-24}{25}$
Jawaban: A
Matematika IPA SBMPTN 2011 No. 5
Kedua akar suku banyak $S(x)={{x}^{2}}-63x+c$ merupakan bilangan prima. Banyak nilai $c$ yang mungkin adalah ….
A. 0
B. 1
C. 2
D. 3
E. lebih dari 3
Pembahasan:
$S(x)={{x}^{2}}-63x+c$, akar-akarnya ${{x}_{1}}$ dan ${{x}_{2}}$ maka:
${{x}_{1}}+{{x}_{2}}=63$ karena ${{x}_{1}}$ dan ${{x}_{2}}$ bilangan prima, maka yang memungkinkan adalah ${{x}_{1}}=2$ dan ${{x}_{2}}=61$.
${{x}_{1}}.{{x}_{2}}=c\Leftrightarrow c=2.61=122$.
Banyak nilai $c$ yang memungkinkan adalah 1.
Jawaban: B
Matematika IPA SBMPTN 2011 No. 6
Diketahui segilima ABCDE, dengan $A(0,2)$, $B(4,0)$, $C(2\pi +1,0)$, $D(2\pi +1,4)$, dan $E(0,4)$. Titik P dipilih secara acak dari titik di dalam segilima tersebut. Peluang sudut APB berukuran tumpul adalah …
A. $\frac{3}{8}$
B. $\frac{1}{4}$
C. $\frac{1}{2}$
D. $\frac{5}{16}$
E. $\frac{5}{8}$
Pembahasan:
Perhatikan gambar berikut ini!

$AB=\sqrt{{{4}^{2}}+{{2}^{2}}}=2\sqrt{5}$
${{L}_{1}}$ = Luas setengah lingkaran dengan diameter AB
${{L}_{1}}=\frac{1}{2}.\frac{1}{4}\pi {{d}^{2}}$
$=\frac{1}{8}\pi {{(2\sqrt{5})}^{2}}$
${{L}_{1}}=\frac{5}{2}\pi $
${{L}_{2}}$ = Luas daerah ABCDE
= Luas OCDE – Luas OAB
$=4(2\pi +1)-\frac{1}{2}.4.2$
${{L}_{2}}$ $=8\pi $
Peluang sudut APB tumbul adalah:
$=\frac{{{L}_{1}}}{{{L}_{2}}}=\frac{\frac{5}{2}\pi }{8\pi }=\frac{5}{16}$
Jawaban: D
Matematika IPA SBMPTN 2011 No. 7
Diketahui limas T.ABC dengan TA tegak lurus bidang ABC. Panjang rusuk AB, AC, BC dan TA berturut-turut adalah 3 cm, 4 cm, 5 cm, dan$\frac{9}{5}$ cm. Jika $\varphi $ sudut antara bidang BCT dengan bidang ABC, maka nilai $\cos \varphi $ adalah …
A. $\frac{4}{5}$
B. $\frac{3}{5}$
C. $\frac{6}{25}$
D. $\frac{9}{25}$
E. $\frac{12}{25}$
Pembahasan:
Perhatikan gambar berikut!

Luas segitiga ABC:
$\frac{1}{2}.AD.BC=\frac{1}{2}.AB.AC$
$AD=\frac{AB.AC}{BC}$
$AD=\frac{3.4}{5}=\frac{12}{5}$
Perhatikan segitiga TAD siku-siku di A, maka:
$TD=\sqrt{A{{D}^{2}}+A{{T}^{2}}}$
$TD=\sqrt{{{\left( \frac{12}{5} \right)}^{2}}+{{\left( \frac{9}{5} \right)}^{2}}}=\frac{15}{5}$
$\cos \alpha =\frac{AE}{TE}=\frac{\frac{12}{5}}{\frac{15}{5}}=\frac{12}{15}=\frac{4}{5}$
Jawaban: A
Matematika IPA SBMPTN 2011 No. 8

Kolam renang berbentuk gabungan persegi panjang dan setengah lingkaran seperti gambar di atas. Keliling kolam renang sama dengan $a$ satuan panjang. Agar luas kolam renang maksimum, maka $x$ = … satuan panjang.
A. $\frac{2a}{\pi }$
B. $\frac{a}{\pi }$
C. $\frac{a}{4+\pi }$
D. $\frac{a}{4+2\pi }$
E. $\frac{2a}{4+\pi }$
Pembahasan:
Keliling = $a$
$x+2y+\frac{1}{2}\pi x=a$
$\left( 1+\frac{1}{2}\pi \right)x+2y=a$
$2y=a-\left( 1+\frac{1}{2}\pi \right)x$
$y=\frac{1}{2}a-\left( \frac{1}{2}+\frac{1}{4}\pi \right)x$
Luas = Luas persegi panjang + Luas setengah lingkaran
$L=x.y+\frac{1}{2}.\frac{1}{4}\pi {{x}^{2}}$
$L=x\left( \frac{1}{2}a-\left( \frac{1}{2}+\frac{1}{4}\pi \right)x \right)+\frac{1}{8}\pi {{x}^{2}}$
$L=\frac{1}{2}ax-\left( \frac{1}{2}+\frac{1}{4}\pi \right){{x}^{2}}+\frac{1}{8}\pi {{x}^{2}}$
$L=\frac{1}{2}ax+\left( -\frac{1}{2}-\frac{1}{4}\pi +\frac{1}{8}\pi \right){{x}^{2}}$
$L=\frac{1}{2}ax+\left( -\frac{1}{2}-\frac{1}{8}\pi \right){{x}^{2}}$
Agar luas maksimum, maka L’ = 0
$\frac{1}{2}a+\left( -1-\frac{1}{4}\pi \right)x=0$
$\frac{1}{2}a=\left( \frac{4+\pi }{4} \right)x$
$2a=\left( 4+\pi \right)x$
$x=\frac{2a}{4+\pi }$
Jawaban: E
Matematika IPA SBMPTN 2011 No. 9
Diberikan $f(x)=a+bx$ dan $F(x)$ adalah anti turunan $f(x)$. Jika $F(1)-F(0)=3$ maka $2a+b$ adalah …
A. 10
B. 6
C. 5
D. 4
E. 3
Pembahasan:
$f(x)=a+bx$
$\int\limits_{0}^{1}{f(x)}dx=F(1)-F(0)$
$\int\limits_{0}^{1}{(a+bx)}dx=3$
$(\left. ax+\frac{1}{2}b{{x}^{2}}) \right|_{0}^{1}=3$
$(a.1+\frac{1}{2}b{{.1}^{2}})-(a.0+\frac{1}{2}b{{.0}^{2}})=3$
$a+\frac{1}{2}b=3$ } kedua ruas dikali 2
$2a+b=6$
Jawaban: B
Matematika IPA SBMPTN 2011 No. 10
Jika $\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{x}=\frac{1}{2}$, maka nilai $\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{\sqrt{1-x}-1}$ adalah …
A. -4
B. -2
C. -1
D. 2
E. 4
Pembahasan:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{\sqrt{1-x}-1}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{\sqrt{1-x}-1}\times \frac{\sqrt{1-x}+1}{\sqrt{1-x}+1}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)(\sqrt{1-x}+1)}{(1-x)-1}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{-x}\times (\sqrt{1-x}+1)$
$=-\underset{x\to 0}{\mathop{\lim }}\,\frac{g(x)}{x}\times (\sqrt{1-x}+1)$
$=-\frac{1}{2}\times (\sqrt{1-0}+1)$
$=-1$
Jawaban: C
Matematika IPA SBMPTN 2011 No. 11
$\cos {{35}^{o}}.\cos {{20}^{o}}-\sin {{35}^{o}}.\sin {{20}^{o}}$ = …
A. $\sin {{35}^{o}}$
B. $\sin {{55}^{o}}$
C. $\cos {{35}^{o}}$
D. $\cos {{15}^{o}}$
E. $\sin {{15}^{o}}$
Pembahasan:
$\cos {{35}^{o}}.\cos {{20}^{o}}-\sin {{35}^{o}}.\sin {{20}^{o}}$
$=\cos ({{35}^{o}}+{{20}^{o}})$
$=\cos {{55}^{o}}$
$=\cos ({{90}^{o}}-{{35}^{o}})$
$=\sin {{35}^{o}}$
Jawaban: A
Matematika IPA SBMPTN 2011 No. 12
Banyak siswa laki-laki 10 orang dan siswa perempuan 5 orang. Banyaknya cara untuk membentuk panitia yang beranggotakan 10 orang dan terdiri atas paling sedikit 2 orang perempuan dan paling banyak 4 orang perempuan adalah …
A. 4800
B. 3150
C. 2700
D. 2300
E. 2250
Pembahasan:
Kemungkinan-kemungkinannya adalah:
2 perempuan dan 8 laki-laki
$=C_{2}^{5}\times C_{8}^{10}=\frac{5!}{2!.3!}\times \frac{10!}{8!.2!}=450$
3 perempuan dan 7 laki-laki
$=C_{3}^{5}\times C_{7}^{10}=\frac{5!}{3!.2!}\times \frac{10!}{7!.3!}=1200$
4 perempuan dan 6 laki-laki
$=C_{4}^{5}\times C_{6}^{10}=\frac{5!}{4!.1!}\times \frac{10!}{6!.4!}=1050$
Seluruhnya = 450 + 1200 + 1050 = 2700
Jawaban: C
Matematika IPA SBMPTN 2011 No. 13
Diketahui $\vec{u}={{p}^{2}}\vec{i}+3\vec{j}-\vec{k}$ dan $\vec{v}=p\vec{i}+p\vec{j}-5\vec{k}$ dengan $-2 < p < 2$. Nilai maksimum $\vec{u}.\vec{v}$ adalah …
A. 8
B. 7
C. 5
D. 4
E. 3
Pembahasan:
$\vec{u}={{p}^{2}}\vec{i}+3\vec{j}-\vec{k}$ dan $\vec{v}=p\vec{i}+p\vec{j}-5\vec{k}$
$\vec{u}.\vec{v}=\left( \begin{matrix} {{p}^{2}} \\ 3 \\ -1 \\ \end{matrix} \right).\left( \begin{matrix} p \\ p \\ -5 \\ \end{matrix} \right)$
$\vec{u}.\vec{v}=-{{p}^{3}}+3p+5$
Agar maksimum maka $(\vec{u}.\vec{v})'=0$, maka:
$-3{{p}^{2}}+3=0$
${{p}^{2}}-1=0$
$(p+1)(p-1)=0$
$p=-1\vee p=1$
Substitusi ke: $\vec{u}.\vec{v}=-{{p}^{3}}+3p+5$
$p=-1\to \vec{u}.\vec{v}=-{{(-1)}^{3}}+3(-1)+5=3$
$p=1\to \vec{u}.\vec{v}=-{{1}^{3}}+3.1+5=7$
Jadi, nilai maksimum $\vec{u}.\vec{v}$ adalah 7.
Jawaban: B
Matematika IPA SBMPTN 2011 No. 14
Persamaan lingkaran dengan pusat $(2,3)$ dan menyinggung garis $y=2x$ adalah …
A. $5{{x}^{2}}+5{{y}^{2}}-20x-30y+12=0$
B. $5{{x}^{2}}+5{{y}^{2}}-20x-30y+49=0$
C. $5{{x}^{2}}+5{{y}^{2}}-20x-30y+54=0$
D. $5{{x}^{2}}+5{{y}^{2}}-20x-30y+60=0$
E. $5{{x}^{2}}+5{{y}^{2}}-20x-30y+64=0$
Pembahasan:
$y=2x\Leftrightarrow 2x-y=0$
$r$ = Jarak titik pusat $(2,3)$ ke garis $2x-y=0$
$r=\left| \frac{2{{x}_{1}}-{{y}_{1}}}{\sqrt{{{2}^{2}}+{{(-1)}^{2}}}} \right|$
$r=\left| \frac{2.2-3}{\sqrt{4+1}} \right|$
$r=\frac{1}{\sqrt{5}}$
Persamaan garis singgung lingkaran dengan pusat $(2,3)$ dan jari-jari $r=\frac{1}{\sqrt{5}}$ adalah:
${{(x-2)}^{2}}+{{(y-3)}^{2}}={{\left( \frac{1}{\sqrt{5}} \right)}^{2}}$
${{x}^{2}}-4x+4+{{y}^{2}}-6y+9=\frac{1}{5}$
$5{{x}^{2}}-20x+20+5{{y}^{2}}-30y+45=1$
$5{{x}^{2}}+5{{y}^{2}}-20x-30y+64=0$
Jawaban: E
Matematika IPA SBMPTN 2011 No. 15
Parabola $y=a{{x}^{2}}+bx+c$ puncaknya $(p,q)$, dicerminkan terhadap garis $y=q$ menghasilkan parabola $y=k{{x}^{2}}+lx+m$. Nilai $a+b+c+k+l+m$ adalah …
A. q
B. 2p
C. p
D. 2q
E. p + q
Pembahasan:
$(x,y)$ dicerminkan terhadap garis $y=q$ bayangannya $(x,2q-y)=(x',y')$, maka substitusikan $x=x'$ dan $y=2q-y'$ ke $y=a{{x}^{2}}+bx+c$, diperoleh:
$2q-y'=a{{(x')}^{2}}+b.x'+c$
$y=-a{{x}^{2}}-bx+2q-c$
$k{{x}^{2}}+lx+m\equiv -a{{x}^{2}}-bx+2q-c$
$k=-a$, $l=-b$, $m=2q-c$
Jadi, nilai
$a+b+c+k+l+m$
$=a+b+c-a-b+2q-c=2q$
$=2q$
Jawaban: D
Artikel Terkait:
|

Post a Comment for "Pembahasan SBMPTN 2011 Matematika IPA"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.