Pembahasan SBMPTN 2012 Matematika IPA Kode 731
Matematika itu tidak sulit. Hanya dibutuhkan banyak berlatih menjawab soal-soal untuk dapat memahaminya dengan baik. Nah, nih Pembahasan Matematika IPA SNMPTN 2012 Kode 731, dan bagi teman-teman yang ingin download soalnya saja, Catatan Matematika selalu menyediakan linknya silahkan di comot sepuasnya dan jangan lupa share buat teman-temannya yang lain ya...!
Matematika IPA SBMPTN 2012 No. 1
Diketahui vektor $\vec{u}$ dan vektor $\vec{v}$ membentuk sudut $\theta $. Jika panjang proyeksi $\vec{u}$ pada $\vec{v}$ sama dengan tiga kali panjang $\vec{v}$, maka perbandingan panjang $\vec{u}$ terhadap panjang $\vec{v}$ adalah …
A. $1:3\cos \theta $
B. $3:\cos \theta $
C. $3\cos \theta :1$
D. $\cos \theta :3$
E. $1:\cos \theta $
Pembahasan:
$\angle (\vec{u},\vec{v})=\theta $, maka: $\vec{u}.\vec{v}=|\vec{u}|.|\vec{v}|.\cos \theta $
panjang proyeksi $\vec{u}$ pada $\vec{v}$ adalah $3.|\vec{v}|$
$\frac{\vec{u}.\vec{v}}{|\vec{v}|}=3.|\vec{v}|$
$\vec{u}.\vec{v}=3.|\vec{v}|.|\vec{v}|$
$|\vec{u}|.|\vec{v}|.\cos \theta =3.|\vec{v}|.|\vec{v}|$
$|\vec{u}|.\cos \theta =3.|\vec{v}|$
$\frac{|\vec{u}|}{|\vec{v}|}=\frac{3}{\cos \theta }$
Jawaban: B
Matematika IPA SBMPTN 2012 No. 2
Vektor $\vec{x}$ diputar terhadap titik asal O sebesar $\theta > 0$ searah jarum jam. Kemudian hasilnya dicerminkan terhadap garis $y=x$, menghasilkan vektor $\vec{y}$. Jika $\vec{y}=A\vec{x}$, maka matriks A = …
A. $\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right]$
B. $\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{matrix} \right]$
C. $\left[ \begin{matrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{matrix}\right]\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right]$
D. $\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix}\right]\left[ \begin{matrix} 0 & -1 \\ -1 & 0 \\ \end{matrix} \right]$
E. $\left[ \begin{matrix} 1 & 0 \\ 0 & -1 \\ \end{matrix} \right]\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right]$
Pembahasan:
Rotasi terhadap titik asal O sebesar $\theta $ searah jarum jam, maka:
${{M}_{1}}=\left[ \begin{matrix} \cos (-\theta ) & -\sin (-\theta ) \\ \sin (-\theta ) & \cos (-\theta ) \\ \end{matrix} \right]$
${{M}_{1}}=\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right]$
Pencerminan terhadap garis $y=x$, maka: ${{M}_{2}}=\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right]$
$\vec{y}=A\vec{x}$
A adalah transformasi matriks ${{M}_{1}}$ dilanjutkan ${{M}_{2}}$ maka:
$A={{M}_{2}}.{{M}_{1}}$
$A=\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right].\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right]$
Jawaban: A
Matematika IPA SBMPTN 2012 No. 3
Luas daerah yang dibatasi oleh kurva $y={{x}^{2}}$, $y=1$, dan $x=2$ adalah …
A. $\int\limits_{-1}^{2}{(1-{{x}^{2}})dx}$
B. $\int\limits_{-1}^{2}{({{x}^{2}}-1)dx}$
C. $\int\limits_{1}^{2}{({{x}^{2}}-1)dx}$
D. $\int\limits_{-1}^{1}{(1-{{x}^{2}})dx}$
E. $\int\limits_{0}^{2}{({{x}^{2}}-1)dx}$
Pembahasan:
Cari titik potong ${{y}_{1}}={{x}^{2}}$ dan ${{y}_{2}}=1$
${{y}_{1}}={{y}_{2}}$
${{x}^{2}}=1$
${{x}^{2}}-1=0\Leftrightarrow (x+1)(x-1)=0$
$x=-1$ atau $x=1$
Perhatikan sketsa gambar berikut!

$L=\int\limits_{1}^{2}{({{y}_{1}}-{{y}_{2}})dx}$
$L=\int\limits_{1}^{2}{({{x}^{2}}-1)dx}$
Jawaban: C
Matematika IPA SBMPTN 2012 No. 4
$\frac{{{(\cos x+\sin x)}^{2}}}{{{(\cos x-\sin x)}^{2}}}$ = …
A. $\frac{1}{1-\cos 2x}$
B. $\frac{1}{1-\sin 2x}$
C. $\frac{1+\cos 2x}{1-\cos 2x}$
D. $\frac{1+2\sin x}{1-2\sin x}$
E. $\frac{1+\sin 2x}{1-\sin 2x}$
Pembahasan:
$\frac{{{(\cos x+\sin x)}^{2}}}{{{(\cos x-\sin x)}^{2}}}$
$=\frac{{{\cos }^{2}}x+2\sin x.\cos x+{{\sin }^{2}}x}{{{\cos }^{2}}x-2\sin x.\cos x+{{\sin }^{2}}x}$
$=\frac{{{\sin }^{2}}x+{{\cos }^{2}}x+2\sin x.\cos x}{{{\sin }^{2}}x+{{\cos }^{2}}x-2\sin x.\cos x}$
$=\frac{1+\sin 2x}{1-\sin 2x}$
Jawaban: E
Matematika IPA SBMPTN 2012 No. 5
Lingkaran ${{(x-3)}^{2}}+{{(y-4)}^{2}}=25$ memotong sumbu X di titik A dan B. Jika P adalah titik pusat lingkaran tersebut, maka $\cos \angle APB$ = …
A. $\frac{7}{25}$
B. $\frac{8}{25}$
C. $\frac{12}{25}$
D. $\frac{18}{25}$
E. $\frac{18}{25}$
Pembahasan:
Perhatikan sketsa lingkaran berikut!
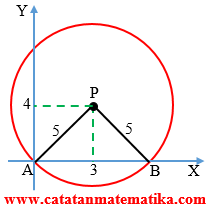
Dari gambar! AP = 5, BP = 5, dan AB = 6, maka dengan menggunakan aturan cosinus diperoleh:
$\cos \angle APB=\frac{A{{P}^{2}}+B{{P}^{2}}-A{{B}^{2}}}{2.AP.BP}$
$\cos \angle APB=\frac{{{5}^{2}}+{{5}^{2}}-{{6}^{2}}}{2.5.5}=\frac{7}{25}$
Jawaban: A
Matematika IPA SBMPTN 2012 No. 6
Tujuh orang berpergian dengan dua mobil milik dua orang di antara mereka. Masing-masing mobil dikemudikan oleh pemiliknya dan kapasitas mobil masing-masing adalah 4 orang termasuk pengemudi. Banyak cara menyusun penumpang di kedua mobil adalah …
A. 10
B. 20
C. 25
D. 28
E. 58
Pembahasan:
Diketahui dari 7 orang hanya dua orang saja yang memiliki mobil, sehingga diperoleh:
$=2\times C_{3}^{7-2}$
$=2\times C_{3}^{5}$
$=2\times \frac{5!}{3!.2!}$
$=2\times \frac{5.4.3!}{3!.2}=20$
Jawaban: B
Matematika IPA SBMPTN 2012 No. 7
Di dalam kotak terdapat 2 bola biru, 4 bola merah, dan 2 bola putih. Jika diambil 7 bola tanpa pengembalian, maka peluang banyak bola merah yang terambil dua kali banyak bola putih yang terambil adalah …
A. $\frac{7}{8}$
B. $\frac{6}{8}$
C. $\frac{5}{8}$
D. $\frac{2}{8}$
E. $\frac{1}{8}$
Pembahasan:
Tersedia 4 bola merah, 2 bola biru, dan 2 bola putih diambil 7 bola.
Peluang banyak bola merah terambil 2 kali banyak bola putih, maka terampil 2 putih, 4 merah, dan 1 biru.
$P=\frac{C_{2}^{2}.C_{4}^{4}.C_{1}^{2}}{C_{7}^{8}}=\frac{1.1.2}{8}=\frac{2}{8}$
Jawaban: D
Matematika IPA SBMPTN 2012 No. 8
Diberikan suku banyak $p(x)=a{{x}^{2}}+bx+1$. Jika $a$ dan $b$ dipilih secara acak dari selang $[0,4]$, maka peluang suku banyak tersebut tidak punya akar adalah …
A. 0
B. $\frac{1}{3}$
C. $\frac{2}{3}$
D. $\frac{5}{6}$
E. 1
Pembahasan:
$p(x)=a{{x}^{2}}+bx+1$ dan $a,b\in [0,4]$
Tidak punya akar maka:
$D < 0$
${{b}^{2}}-4ac < 0$
${{b}^{2}}-4a < 0 \Leftrightarrow \frac{1}{4}{{b}^{2}} < a$
Perhatikan sketsa grafik berikut!

Peluang tidak memiliki akar adalah:
$=\frac{{{L}_{arsir}}}{{{L}_{persegi}}}=\frac{\frac{2}{3}.4.4}{4.4}=\frac{2}{3}$
Jawaban: C
Matematika IPA SBMPTN 2012 No. 9
Nilai $\cos x-\sin x < 0$, jika …
A. $\frac{\pi }{5} < x < \frac{\pi }{3}$
B. $\frac{2\pi }{3} < x < \frac{7\pi }{5}$
C. $\frac{\pi }{5} < x < \frac{\pi }{2}$
D. $\frac{\pi }{4} < x < \frac{6\pi }{5}$
E. $\frac{2\pi }{3} < x < \frac{8\pi }{9}$
Pembahasan:
Perhatikan sketsa grafik cos x dan sin x berikut ini!
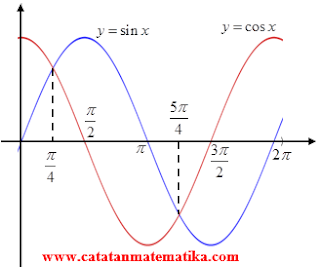
$\cos x-\sin x < 0$
$\cos x < \sin x$ (artinya grafik cos x di bawah grafik sin x), hal ini terjadi pada interval $\frac{\pi }{4} < x < \frac{5\pi }{4}$.
Opsi yang memenuhi adalah D.
Jawaban: D
Matematika IPA SBMPTN 2012 No. 10
$\underset{x\to 0}{\mathop{\lim }}\,\frac{1-{{\cos }^{2}}x}{{{x}^{2}}.\cot \left( x+\frac{\pi }{4} \right)}$ = …
A. -1
B. 0
C. 1
D. $\frac{\sqrt{2}}{2}$
E. $\sqrt{3}$
Pembahasan:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{1-{{\cos }^{2}}x}{{{x}^{2}}.\cot \left( x+\frac{\pi }{4} \right)}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{{{\sin }^{2}}x}{{{x}^{2}}.\cot \left( x+\frac{\pi }{4} \right)}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{{{\sin }^{2}}x}{{{x}^{2}}}.\tan \left( x+\frac{\pi }{4} \right)$
$=1.\tan \left( 0+\frac{\pi }{4} \right)$
$=1$
Jawaban: C
Matematika IPA SBMPTN 2012 No. 11
Lingkaran ${{(x-6)}^{2}}+{{(y+1)}^{2}}=25$ menyinggung garis $y=4$ di titik …
A. (-1,4)
B. (1,4)
C. (6,4)
D. (-6,4)
E. (5,4)
Pembahasan:
$y=4$ substitusi ke:
${{(x-6)}^{2}}+{{(y+1)}^{2}}=25$
${{(x-6)}^{2}}+{{(4+1)}^{2}}=25$
${{(x-6)}^{2}}=0\Leftrightarrow x=6$
Titik singgung $(6,4)$
Jawaban: C
Matematika IPA SBMPTN 2012 No. 12
Jika $2{{x}^{3}}-5{{x}^{2}}-kx+18$ dibagi $x-1$ mempunyai sisa 10, maka nilai $k$ adalah …
A. -15
B. -5
C. 0
D. 2
E. 5
Pembahasan:
Dengan menggunakan teorema sisa:
$f(x)=2{{x}^{3}}-5{{x}^{2}}-kx+18$ dibagi $x-1$ maka sisa = $f(1)=10$.
$f(1)={{2.1}^{3}}-{{5.1}^{2}}-k.1+18$
$10=15-k\Leftrightarrow k=5$
Jawaban: E
Matematika IPA SBMPTN 2012 No. 13
Diberikan persamaan $\cos x=\frac{a-1,5}{2-0,5a}$. Banyak bilangan bulat $a$ sehingga persamaan tersebut mempunyai selesaian adalah …
A. 1
B. 2
C. 3
D. 4
E. 6
Pembahasan:
$\cos x=\frac{a-1,5}{2-0,5a}$
$\cos x=\frac{2a-3}{4-a}$
$-1\le \cos x\le 1$
$-1\le \frac{2a-3}{4-a}\le 1$
$\left| \frac{2a-3}{4-a} \right|\le 1$
$\left| 2a-3 \right|\le \left| 4-a \right|$
$(2a-3+4-a)[2a-3-(4-a)]\le 0$
$(a+1)(3a-7)\le 0$
$-1\le a\le \frac{7}{3}$
$a=\left\{ -1,0,1,2 \right\}$
Jadi, ada 4 nilai $a$ yang memenuhi.
Jawaban: D
Matematika IPA SBMPTN 2012 No. 14
Diberikan limas T.ABC dengan AB = AC = BC = 6 dan TA = TB = TC = 5. Jarak titik T ke bidang ABC adalah …
A. $\sqrt{18}$
B. $\sqrt{13}$
C. 4
D. $\frac{5}{2}\sqrt{3}$
E. $2\sqrt{3}$
Pembahasan:
Perhatikan gambar berikut ini!
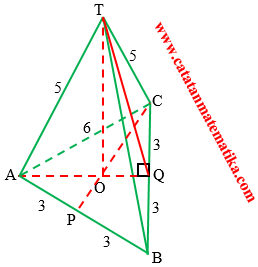
Segitiga ABC adalah segitiga sama sisi, maka $\angle ACQ={{60}^{o}}$ dan $\angle OCQ={{30}^{o}}$, sehingga pada segitiga CQO siku-siku di Q berlaku:
$\cos \angle OCQ=\frac{CQ}{OC}$
$\cos {{30}^{o}}=\frac{3}{OC}$
$\frac{1}{2}\sqrt{3}=\frac{3}{OC}\Leftrightarrow OC=\frac{6}{\sqrt{3}}=2\sqrt{3}$
Perhatikan segitiga TOC siku-siku di O, berlaku teorema phytagoras:
$OT=\sqrt{T{{C}^{2}}-O{{C}^{2}}}$
$OT=\sqrt{{{5}^{2}}-{{(2\sqrt{3})}^{2}}}$
$OT=\sqrt{13}$
Jawaban: B
Matematika IPA SBMPTN 2012 No. 15
Grafik fungsi $f(x)=a{{x}^{3}}+b{{x}^{2}}+cx-12$ naik jika …
A. ${{b}^{2}}-4ac < 0$ dan $a > 0$
B. ${{b}^{2}}-4ac < 0$ dan $a < 0$
C. ${{b}^{2}}-3ac > 0$ dan $a > 0$
D. ${{b}^{2}}-3ac < 0$ dan $a < 0$
E. ${{b}^{2}}-3ac < 0$ dan $a > 0$
Pembahasan:
$f(x)=a{{x}^{3}}+b{{x}^{2}}+cx-12$
$f(x)$ naik jika $f'(x) > 0$
$f(x)=3a{{x}^{2}}+2bx+c$
$3a{{x}^{2}}+2bx+c > 0$ (definit positif), maka:
*) $D < 0$
${{(2b)}^{2}}-4.3a.c < 0$
$4{{b}^{2}}-12ac < 0 \Leftrightarrow {{b}^{2}}-3ac < 0$
*) $A > 0$
$3a > 0 \Leftrightarrow a > 0$
Jawaban: E
Matematika IPA SBMPTN 2012 No. 1
Diketahui vektor $\vec{u}$ dan vektor $\vec{v}$ membentuk sudut $\theta $. Jika panjang proyeksi $\vec{u}$ pada $\vec{v}$ sama dengan tiga kali panjang $\vec{v}$, maka perbandingan panjang $\vec{u}$ terhadap panjang $\vec{v}$ adalah …
A. $1:3\cos \theta $
B. $3:\cos \theta $
C. $3\cos \theta :1$
D. $\cos \theta :3$
E. $1:\cos \theta $
Pembahasan:
$\angle (\vec{u},\vec{v})=\theta $, maka: $\vec{u}.\vec{v}=|\vec{u}|.|\vec{v}|.\cos \theta $
panjang proyeksi $\vec{u}$ pada $\vec{v}$ adalah $3.|\vec{v}|$
$\frac{\vec{u}.\vec{v}}{|\vec{v}|}=3.|\vec{v}|$
$\vec{u}.\vec{v}=3.|\vec{v}|.|\vec{v}|$
$|\vec{u}|.|\vec{v}|.\cos \theta =3.|\vec{v}|.|\vec{v}|$
$|\vec{u}|.\cos \theta =3.|\vec{v}|$
$\frac{|\vec{u}|}{|\vec{v}|}=\frac{3}{\cos \theta }$
Jawaban: B
Matematika IPA SBMPTN 2012 No. 2
Vektor $\vec{x}$ diputar terhadap titik asal O sebesar $\theta > 0$ searah jarum jam. Kemudian hasilnya dicerminkan terhadap garis $y=x$, menghasilkan vektor $\vec{y}$. Jika $\vec{y}=A\vec{x}$, maka matriks A = …
A. $\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right]$
B. $\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{matrix} \right]$
C. $\left[ \begin{matrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{matrix}\right]\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right]$
D. $\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix}\right]\left[ \begin{matrix} 0 & -1 \\ -1 & 0 \\ \end{matrix} \right]$
E. $\left[ \begin{matrix} 1 & 0 \\ 0 & -1 \\ \end{matrix} \right]\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right]$
Pembahasan:
Rotasi terhadap titik asal O sebesar $\theta $ searah jarum jam, maka:
${{M}_{1}}=\left[ \begin{matrix} \cos (-\theta ) & -\sin (-\theta ) \\ \sin (-\theta ) & \cos (-\theta ) \\ \end{matrix} \right]$
${{M}_{1}}=\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right]$
Pencerminan terhadap garis $y=x$, maka: ${{M}_{2}}=\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right]$
$\vec{y}=A\vec{x}$
A adalah transformasi matriks ${{M}_{1}}$ dilanjutkan ${{M}_{2}}$ maka:
$A={{M}_{2}}.{{M}_{1}}$
$A=\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right].\left[ \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right]$
Jawaban: A
Matematika IPA SBMPTN 2012 No. 3
Luas daerah yang dibatasi oleh kurva $y={{x}^{2}}$, $y=1$, dan $x=2$ adalah …
A. $\int\limits_{-1}^{2}{(1-{{x}^{2}})dx}$
B. $\int\limits_{-1}^{2}{({{x}^{2}}-1)dx}$
C. $\int\limits_{1}^{2}{({{x}^{2}}-1)dx}$
D. $\int\limits_{-1}^{1}{(1-{{x}^{2}})dx}$
E. $\int\limits_{0}^{2}{({{x}^{2}}-1)dx}$
Pembahasan:
Cari titik potong ${{y}_{1}}={{x}^{2}}$ dan ${{y}_{2}}=1$
${{y}_{1}}={{y}_{2}}$
${{x}^{2}}=1$
${{x}^{2}}-1=0\Leftrightarrow (x+1)(x-1)=0$
$x=-1$ atau $x=1$
Perhatikan sketsa gambar berikut!

$L=\int\limits_{1}^{2}{({{y}_{1}}-{{y}_{2}})dx}$
$L=\int\limits_{1}^{2}{({{x}^{2}}-1)dx}$
Jawaban: C
Matematika IPA SBMPTN 2012 No. 4
$\frac{{{(\cos x+\sin x)}^{2}}}{{{(\cos x-\sin x)}^{2}}}$ = …
A. $\frac{1}{1-\cos 2x}$
B. $\frac{1}{1-\sin 2x}$
C. $\frac{1+\cos 2x}{1-\cos 2x}$
D. $\frac{1+2\sin x}{1-2\sin x}$
E. $\frac{1+\sin 2x}{1-\sin 2x}$
Pembahasan:
$\frac{{{(\cos x+\sin x)}^{2}}}{{{(\cos x-\sin x)}^{2}}}$
$=\frac{{{\cos }^{2}}x+2\sin x.\cos x+{{\sin }^{2}}x}{{{\cos }^{2}}x-2\sin x.\cos x+{{\sin }^{2}}x}$
$=\frac{{{\sin }^{2}}x+{{\cos }^{2}}x+2\sin x.\cos x}{{{\sin }^{2}}x+{{\cos }^{2}}x-2\sin x.\cos x}$
$=\frac{1+\sin 2x}{1-\sin 2x}$
Jawaban: E
Matematika IPA SBMPTN 2012 No. 5
Lingkaran ${{(x-3)}^{2}}+{{(y-4)}^{2}}=25$ memotong sumbu X di titik A dan B. Jika P adalah titik pusat lingkaran tersebut, maka $\cos \angle APB$ = …
A. $\frac{7}{25}$
B. $\frac{8}{25}$
C. $\frac{12}{25}$
D. $\frac{18}{25}$
E. $\frac{18}{25}$
Pembahasan:
Perhatikan sketsa lingkaran berikut!

Dari gambar! AP = 5, BP = 5, dan AB = 6, maka dengan menggunakan aturan cosinus diperoleh:
$\cos \angle APB=\frac{A{{P}^{2}}+B{{P}^{2}}-A{{B}^{2}}}{2.AP.BP}$
$\cos \angle APB=\frac{{{5}^{2}}+{{5}^{2}}-{{6}^{2}}}{2.5.5}=\frac{7}{25}$
Jawaban: A
Matematika IPA SBMPTN 2012 No. 6
Tujuh orang berpergian dengan dua mobil milik dua orang di antara mereka. Masing-masing mobil dikemudikan oleh pemiliknya dan kapasitas mobil masing-masing adalah 4 orang termasuk pengemudi. Banyak cara menyusun penumpang di kedua mobil adalah …
A. 10
B. 20
C. 25
D. 28
E. 58
Pembahasan:
Diketahui dari 7 orang hanya dua orang saja yang memiliki mobil, sehingga diperoleh:
$=2\times C_{3}^{7-2}$
$=2\times C_{3}^{5}$
$=2\times \frac{5!}{3!.2!}$
$=2\times \frac{5.4.3!}{3!.2}=20$
Jawaban: B
Matematika IPA SBMPTN 2012 No. 7
Di dalam kotak terdapat 2 bola biru, 4 bola merah, dan 2 bola putih. Jika diambil 7 bola tanpa pengembalian, maka peluang banyak bola merah yang terambil dua kali banyak bola putih yang terambil adalah …
A. $\frac{7}{8}$
B. $\frac{6}{8}$
C. $\frac{5}{8}$
D. $\frac{2}{8}$
E. $\frac{1}{8}$
Pembahasan:
Tersedia 4 bola merah, 2 bola biru, dan 2 bola putih diambil 7 bola.
Peluang banyak bola merah terambil 2 kali banyak bola putih, maka terampil 2 putih, 4 merah, dan 1 biru.
$P=\frac{C_{2}^{2}.C_{4}^{4}.C_{1}^{2}}{C_{7}^{8}}=\frac{1.1.2}{8}=\frac{2}{8}$
Jawaban: D
Matematika IPA SBMPTN 2012 No. 8
Diberikan suku banyak $p(x)=a{{x}^{2}}+bx+1$. Jika $a$ dan $b$ dipilih secara acak dari selang $[0,4]$, maka peluang suku banyak tersebut tidak punya akar adalah …
A. 0
B. $\frac{1}{3}$
C. $\frac{2}{3}$
D. $\frac{5}{6}$
E. 1
Pembahasan:
$p(x)=a{{x}^{2}}+bx+1$ dan $a,b\in [0,4]$
Tidak punya akar maka:
$D < 0$
${{b}^{2}}-4ac < 0$
${{b}^{2}}-4a < 0 \Leftrightarrow \frac{1}{4}{{b}^{2}} < a$
Perhatikan sketsa grafik berikut!

Peluang tidak memiliki akar adalah:
$=\frac{{{L}_{arsir}}}{{{L}_{persegi}}}=\frac{\frac{2}{3}.4.4}{4.4}=\frac{2}{3}$
Jawaban: C
Matematika IPA SBMPTN 2012 No. 9
Nilai $\cos x-\sin x < 0$, jika …
A. $\frac{\pi }{5} < x < \frac{\pi }{3}$
B. $\frac{2\pi }{3} < x < \frac{7\pi }{5}$
C. $\frac{\pi }{5} < x < \frac{\pi }{2}$
D. $\frac{\pi }{4} < x < \frac{6\pi }{5}$
E. $\frac{2\pi }{3} < x < \frac{8\pi }{9}$
Pembahasan:
Perhatikan sketsa grafik cos x dan sin x berikut ini!

$\cos x-\sin x < 0$
$\cos x < \sin x$ (artinya grafik cos x di bawah grafik sin x), hal ini terjadi pada interval $\frac{\pi }{4} < x < \frac{5\pi }{4}$.
Opsi yang memenuhi adalah D.
Jawaban: D
Matematika IPA SBMPTN 2012 No. 10
$\underset{x\to 0}{\mathop{\lim }}\,\frac{1-{{\cos }^{2}}x}{{{x}^{2}}.\cot \left( x+\frac{\pi }{4} \right)}$ = …
A. -1
B. 0
C. 1
D. $\frac{\sqrt{2}}{2}$
E. $\sqrt{3}$
Pembahasan:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{1-{{\cos }^{2}}x}{{{x}^{2}}.\cot \left( x+\frac{\pi }{4} \right)}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{{{\sin }^{2}}x}{{{x}^{2}}.\cot \left( x+\frac{\pi }{4} \right)}$
$=\underset{x\to 0}{\mathop{\lim }}\,\frac{{{\sin }^{2}}x}{{{x}^{2}}}.\tan \left( x+\frac{\pi }{4} \right)$
$=1.\tan \left( 0+\frac{\pi }{4} \right)$
$=1$
Jawaban: C
Matematika IPA SBMPTN 2012 No. 11
Lingkaran ${{(x-6)}^{2}}+{{(y+1)}^{2}}=25$ menyinggung garis $y=4$ di titik …
A. (-1,4)
B. (1,4)
C. (6,4)
D. (-6,4)
E. (5,4)
Pembahasan:
$y=4$ substitusi ke:
${{(x-6)}^{2}}+{{(y+1)}^{2}}=25$
${{(x-6)}^{2}}+{{(4+1)}^{2}}=25$
${{(x-6)}^{2}}=0\Leftrightarrow x=6$
Titik singgung $(6,4)$
Jawaban: C
Matematika IPA SBMPTN 2012 No. 12
Jika $2{{x}^{3}}-5{{x}^{2}}-kx+18$ dibagi $x-1$ mempunyai sisa 10, maka nilai $k$ adalah …
A. -15
B. -5
C. 0
D. 2
E. 5
Pembahasan:
Dengan menggunakan teorema sisa:
$f(x)=2{{x}^{3}}-5{{x}^{2}}-kx+18$ dibagi $x-1$ maka sisa = $f(1)=10$.
$f(1)={{2.1}^{3}}-{{5.1}^{2}}-k.1+18$
$10=15-k\Leftrightarrow k=5$
Jawaban: E
Matematika IPA SBMPTN 2012 No. 13
Diberikan persamaan $\cos x=\frac{a-1,5}{2-0,5a}$. Banyak bilangan bulat $a$ sehingga persamaan tersebut mempunyai selesaian adalah …
A. 1
B. 2
C. 3
D. 4
E. 6
Pembahasan:
$\cos x=\frac{a-1,5}{2-0,5a}$
$\cos x=\frac{2a-3}{4-a}$
$-1\le \cos x\le 1$
$-1\le \frac{2a-3}{4-a}\le 1$
$\left| \frac{2a-3}{4-a} \right|\le 1$
$\left| 2a-3 \right|\le \left| 4-a \right|$
$(2a-3+4-a)[2a-3-(4-a)]\le 0$
$(a+1)(3a-7)\le 0$
$-1\le a\le \frac{7}{3}$
$a=\left\{ -1,0,1,2 \right\}$
Jadi, ada 4 nilai $a$ yang memenuhi.
Jawaban: D
Matematika IPA SBMPTN 2012 No. 14
Diberikan limas T.ABC dengan AB = AC = BC = 6 dan TA = TB = TC = 5. Jarak titik T ke bidang ABC adalah …
A. $\sqrt{18}$
B. $\sqrt{13}$
C. 4
D. $\frac{5}{2}\sqrt{3}$
E. $2\sqrt{3}$
Pembahasan:
Perhatikan gambar berikut ini!

Segitiga ABC adalah segitiga sama sisi, maka $\angle ACQ={{60}^{o}}$ dan $\angle OCQ={{30}^{o}}$, sehingga pada segitiga CQO siku-siku di Q berlaku:
$\cos \angle OCQ=\frac{CQ}{OC}$
$\cos {{30}^{o}}=\frac{3}{OC}$
$\frac{1}{2}\sqrt{3}=\frac{3}{OC}\Leftrightarrow OC=\frac{6}{\sqrt{3}}=2\sqrt{3}$
Perhatikan segitiga TOC siku-siku di O, berlaku teorema phytagoras:
$OT=\sqrt{T{{C}^{2}}-O{{C}^{2}}}$
$OT=\sqrt{{{5}^{2}}-{{(2\sqrt{3})}^{2}}}$
$OT=\sqrt{13}$
Jawaban: B
Matematika IPA SBMPTN 2012 No. 15
Grafik fungsi $f(x)=a{{x}^{3}}+b{{x}^{2}}+cx-12$ naik jika …
A. ${{b}^{2}}-4ac < 0$ dan $a > 0$
B. ${{b}^{2}}-4ac < 0$ dan $a < 0$
C. ${{b}^{2}}-3ac > 0$ dan $a > 0$
D. ${{b}^{2}}-3ac < 0$ dan $a < 0$
E. ${{b}^{2}}-3ac < 0$ dan $a > 0$
Pembahasan:
$f(x)=a{{x}^{3}}+b{{x}^{2}}+cx-12$
$f(x)$ naik jika $f'(x) > 0$
$f(x)=3a{{x}^{2}}+2bx+c$
$3a{{x}^{2}}+2bx+c > 0$ (definit positif), maka:
*) $D < 0$
${{(2b)}^{2}}-4.3a.c < 0$
$4{{b}^{2}}-12ac < 0 \Leftrightarrow {{b}^{2}}-3ac < 0$
*) $A > 0$
$3a > 0 \Leftrightarrow a > 0$
Jawaban: E
Artikel Terkait:
|

Post a Comment for "Pembahasan SBMPTN 2012 Matematika IPA Kode 731"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.