Pembahasan SBMPTN 2017 Matematika Dasar Kode 232
Kalian sekarang kelas XII SMA? Pengen melanjutkan studi ke jenjang perguruan tinggi? Punya Harapan ingin masuk Perguruan Tinggi Negeri yang diidam-idamkan? Syaratnya... kamu harus lulus SBMPTN (Seleksi Bersama Masuk Perguruan Tinggi Negeri), dan untuk bisa menjadi salah satu mahasiswa di PTN maka adik-adik kudu belajar dari sekarang. Nih Catatan Matematika berbagi Soal dan Pembahasan Matematika Dasar SBMPTN 2017 kode 232. Lho... tunggu apalagi? Silahkan di download soalnya dan lirik pembahasannya di postingan ini. Semangat...! Semoga kalian lulus ya...!
Matematika Dasar SBMPTN 2017 No. 46
Misalkan ${{A}^{T}}$ adalah transpose matriks A dan $I=\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right)$. Jika $A=\left( \begin{matrix} a & b \\ 0 & 3 \\ \end{matrix} \right)$ sehingga $2A+3{{A}^{T}}=15I$, maka nilai ${{a}^{2}}+{{b}^{2}}$ adalah …
A. 2
B. 4
C. 5
D. 8
E. 9
Pembahasan:
$2A+3{{A}^{T}}=15I$
$2\left( \begin{matrix} a & b \\ 0 & 3 \\ \end{matrix} \right)+3\left( \begin{matrix} a & 0 \\ b & 3 \\ \end{matrix} \right)=15\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right)$
$\left( \begin{matrix} 2a & 2b \\ 0 & 6 \\ \end{matrix} \right)+\left( \begin{matrix} 3a & 0 \\ 3b & 9 \\ \end{matrix} \right)=\left( \begin{matrix} 15 & 0 \\ 0 & 15 \\ \end{matrix} \right)$
$\left( \begin{matrix} 5a & 2b \\ 3b & 15 \\ \end{matrix} \right)=\left( \begin{matrix} 15 & 0 \\ 0 & 15 \\ \end{matrix} \right)$
$5a=15\Leftrightarrow a=3$
$2b=0\Leftrightarrow b=0$
Nilai ${{a}^{2}}+{{b}^{2}}={{3}^{2}}+{{0}^{2}}=9$
Jawaban: E
Matematika Dasar SBMPTN 2017 No. 47
Jika himpunan penyelesaian $|2x-a| < 5$ adalah {$x|-1 < x < 4$}, maka nilai $a$ adalah …
A. -4
B. -3
C. -1
D. 3
E. 4
Pembahasan:
$|2x-a| < 5$
$-5 < 2x-a < 5$
$-5+a < 2x < 5+a$
$\frac{-5+a}{2} < x < \frac{5+a}{2}$ ekuivalen dengan $-1 < x < 4$, maka:
$\frac{5+a}{2}=4\Leftrightarrow 5+a=8\Leftrightarrow a=3$
Jawaban: D
Matematika Dasar SBMPTN 2017 No. 48

Pada segitiga siku-siku samakaki ABC, sisi AB dan BC masing-masing terbagi menjadi tiga bagian yang sama, berturut-turut oleh titik K, L, M, dan N. Jika luas segitiga ABC adalah $x$ $c{{m}^{2}}$, maka luas segitiga KMN adalah … $c{{m}^{2}}$.
A. $\frac{x}{3}$
B. $\frac{2x}{9}$
C. $\frac{x}{9}$
D. $\frac{x}{18}$
E. $\frac{x}{36}$
Pembahasan:
Perhatikan gambar.
Misalkan BC = AC = $y$
Sehingga luas ABC:
$\frac{1}{2}{{y}^{2}}=x$
BM = MN = NC = $\frac{1}{3}y$ serta BK = $\frac{2}{3}y$.
Luas segitiga KMN dengan alas = MN dan tinggi = BK adalah:
= $\frac{1}{2}.\frac{1}{3}y.\frac{2}{3}y=\frac{2}{9}.\frac{1}{2}{{y}^{2}}$
= $\frac{2}{9}.\frac{1}{2}{{y}^{2}}$
= $\frac{2}{9}.x=\frac{2x}{9}$
Jawaban: B
Matematika Dasar SBMPTN 2017 No. 49
Jika $f(x)=\sqrt{x-1}$ dan $g(x)=\frac{x-5}{x-1}$, $x\ne 1$, maka daerah asal $f.g$ adalah …
A. $-\infty < x < \infty $
B. $x\ne 0$
C. $x\ne 1$
D. $x\ge 1$
E. $x > 1$
Pembahasan:
$f.g=\sqrt{x-1}.\frac{x-5}{x-1}$
$f.g=\frac{(x-5)\sqrt{x-1}}{x-1}$
Daerah asal $f.g$ yaitu:
i) syarat bentuk akar $\sqrt{x-1}$ adalah $x-1\ge 0\Leftrightarrow x\ge 1$
ii) syarat penyebut $x-1\ne 0\Leftrightarrow x\ne 1$
dari i) dan ii) diperoleh:
Daerah asal $f.g$ adalah $x > 1$
Jawaban: E
Matematika Dasar SBMPTN 2017 No. 50
Diketahui median dan rata-rata berat badan 5 balita adalah sama. Setelah ditambahkan satu data berat badan balita, rata-ratanya meningkat 1 kg, sedangkan mediannya tetap. Jika 6 data berat badan tersebut diurutkan dari yang paling ringan ke yang paling berat, maka selisih berat badan antara balita terakhir yang ditambahkan dan balita di urutan ke-4 adalah … kg.
A. 4
B. $\frac{9}{2}$
C. 5
D. 6
E. $\frac{13}{2}$
Pembahasan:
Setelah diurutkan berat badan kelima balita itu adalah:
$a$, $b$, $c$, $d$, $e$
$Me=c=\bar{x}$
$\bar{x}=\frac{a+b+c+d+e}{5}=c$, maka:
$a+b+c+d+e=5c$.
Jika ditambah data berat badan seorang balita lagi, misalkan $f$, maka rata-ratanya naik 1 dan mediannya tetap, artinya:
*) karena rata-rata mengalami kenaikan maka dapatlah disimpulkan bahwa $f$ data terbesar.
*) $a$, $b$, $c$, $d$, $e$, $f$
$Me=c$, maka $d=c$
*) rata-rata menjadi:
$\frac{a+b+c+d+e+f}{6}=c+1$
$\frac{5c+f}{6}=c+1$
$5c+f=6c+6$
$f-c=6$
Selisih berat badan balita ke-6 ($f$) dengan balita urutan ke-4 ($d$) adalah:
$f-d=f-c=6$
Jawaban: D
Matematika Dasar SBMPTN 2017 No. 51
Jumlah suku ke-3 dan ke-7 suatu barisan aritmetika dengan suku-sukunya bilangan asli adalah 28. Jika beda barisan tersebut 3, maka suku ke-7 adalah …
A. 19
B. 20
C. 21
D. 22
E. 23
Pembahasan:
Barisan Aritmetika: ${{U}_{n}}=a+(n-1)b$
${{U}_{3}}+{{U}_{7}}=28$
$(a+2b)+(a+6b)=28$
$2a+8b=28$
$a+4b=14$; $b=3$
$a+4.3=14\Leftrightarrow a=2$
${{U}_{7}}=a+6b=2+6.3=20$
Jawaban: B
Matematika Dasar SBMPTN 2017 No. 52
Seseorang memelihara ikan di suatu kolam. Rata-rata bobot ikan per ekor pada saat panen dari kolam tersebut adalah $(6-0,02x)$ kg, dengan $x$ menyatakan banyak ikan yang dipelihara. Maksimum total bobot semua ikan pada saat panen yang mungkin adalah … kg.
A. 400
B. 420
C. 435
D. 450
E. 465
Pembahasan:
Total bobot semua ikan adalah:
$f(x)=(6-0,02x)x=6x-0,02{{x}^{2}}$.
Agar total maksimum, maka $f'(x)=0$
$f(x)=6x-0,02{{x}^{2}}$
$f'(x)=6-0,04x=0$
$0,04x=6\Leftrightarrow x=\frac{6}{0,04}=150$
$f(150)=(6-0,02.(150)).150$
$f(150)=(6-3).150=450$
Maka total bobot maksimum adalah 450 kg.
Jawaban: D
Matematika Dasar SBMPTN 2017 No. 53
Lima bilangan asli membentuk barisan geometri dengan rasio positif. Jika jumlah 3 suku terbesar dan jumlah 3 suku terkecil barisan geometri berturut-turut adalah 171 dan 76, maka jumlah 5 bilangan tersebut adalah …
A. 125
B. 130
C. 180
D. 211
E. 347
Pembahasan:
Barisan Geometri: ${{U}_{n}}=a{{r}^{n-1}}$,
${{U}_{1}},{{U}_{2}},{{U}_{3}},{{U}_{4}},{{U}_{5}}$ $r > 0$
Jumlah 3 suku terbesar adalah 171, maka:
${{U}_{3}}+{{U}_{4}}+{{U}_{5}}=171$
$a{{r}^{2}}+a{{r}^{3}}+a{{r}^{4}}=171$
$a{{r}^{2}}(1+r+{{r}^{2}})=171$ …. Persamaan (1)
Jumlah 3 suku terbesar adalah 76, maka:
${{U}_{1}}+{{U}_{2}}+{{U}_{3}}=76$
$a+ar+a{{r}^{2}}=76$
$a(1+r+{{r}^{2}})=76$ …. Persamaan (2)
Persamaan (1) dibagi dengan persamaan (2), maka:
$\frac{a{{r}^{2}}(1+r+{{r}^{2}})}{a(1+r+{{r}^{2}})}=\frac{171}{76}$
${{r}^{2}}=\frac{9}{4}\Leftrightarrow r=\frac{3}{2}$
Substitusi ke persamaan (2):
$a(1+r+{{r}^{2}})=76$
$a\left( 1+\frac{3}{2}+{{\left( \frac{3}{2} \right)}^{2}} \right)=76$
$a\left( 1+\frac{3}{2}+\frac{9}{4} \right)=76$
$\frac{19}{4}a=76\Leftrightarrow a=16$
${{S}_{n}}=\frac{a({{r}^{n}}-1)}{r-1}$
${{S}_{5}}=\frac{16\left( {{\left( \frac{3}{2} \right)}^{5}}-1 \right)}{\frac{3}{2}-1}$
${{S}_{5}}=\frac{16\left( \frac{243}{32}-1 \right)}{\frac{1}{2}}$
${{S}_{5}}=32.\frac{211}{32}=211$
Jawaban: D
Matematika Dasar SBMPTN 2017 No. 54
Jika $f(x)={{x}^{2}}+2$ dan $g(x)=-3x+8$, maka nilai maksimum fungsi $(g\circ f)(x)$ adalah …
A. 0
B. 1
C. 2
D. 3
E. 4
Pembahasan:
$\begin{align} (g\circ f)(x) &=g(f(x)) \\ &=g({{x}^{2}}+2) \\ & =-3({{x}^{2}}+2)+8 \\ (g\circ f)(x) &=-3{{x}^{2}}+2
\end{align}$
Nilai maksimum diperoleh jika:
$(g\circ f)'(x)=0$
$-6x=0\Leftrightarrow x=0$
$(g\circ f)(x)=-3{{x}^{2}}+2$
$(g\circ f)(0)=-{{3.0}^{2}}+2=2$
Jawaban: C
Matematika Dasar SBMPTN 2017 No. 55
Diketahui kubus ABCD.EFGH dengan titik P terletak pada perpanjangan BF sehingga FP = 3 cm dan garis AP berpotongan dengan garis EF di titik Q. Jika panjang rusuk kubus tersebut adalah 6 cm, maka jarak Q ke D adalah … cm.
A. $2\sqrt{13}$
B. $2\sqrt{18}$
C. $2\sqrt{22}$
D. $4\sqrt{7}$
E. $4\sqrt{11}$
Pembahasan:
Perhatikan gambar berikut!
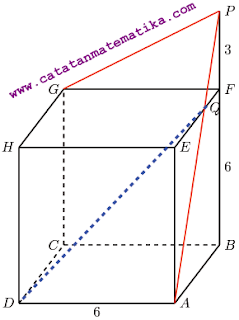
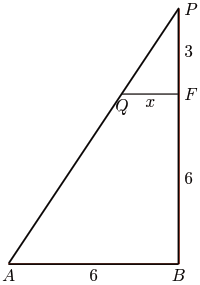
Segitiga ABP sebangun dengan segitiga QFP, maka berlaku:
$\frac{x}{6}=\frac{3}{3+6}\Leftrightarrow \frac{x}{6}=\frac{3}{9}\Leftrightarrow x=2$
Karena $QF=x=2$, maka $EQ=6-2=4$ sehingga:
$A{{Q}^{2}}=E{{Q}^{2}}+E{{A}^{2}}$
$A{{Q}^{2}}={{4}^{2}}+{{6}^{2}}=52$
Perhatikan segitiga DAQ siku-siku di A, maka:
$\begin{align} DQ &= \sqrt{D{{A}^{2}}+A{{Q}^{2}}} \\ & =\sqrt{{{6}^{2}}+52} \\ & =\sqrt{88} \\ DQ &=2\sqrt{22} \end{align}$
Jawaban: C
Matematika Dasar SBMPTN 2017 No. 56
Luas daerah penyelesaian sistem pertidaksamaan $y+4x\le 12$, $y+2x\ge 8$, $x\ge 0$ adalah … satuan luas.
A. 2
B. 4
C. 6
D. 8
E. 10
Pembahasan:
Derah penyelesaian dari sistem pertidaksamaan tersebut adalah daerah yang diarsir pada gambar berikut!
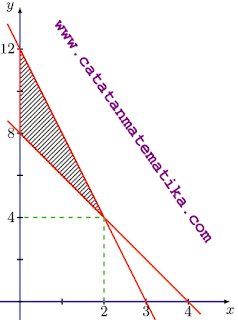
Derah yang diarsir merupakan segitiga yang alasnya $a=12-8=4$ dan tingginya $t=2$.
Jadi, luasnya adalah:
L = $\frac{1}{2}.a.t$
L = $\frac{1}{2}.4.2=4$
Jawaban: B
Matematika Dasar SBMPTN 2017 No. 57
Transformasi yang bersesuaian dengan matriks $A=\left( \begin{matrix} 0 & a \\ b & 0 \\ \end{matrix} \right)$ memetakan titik $(1,2)$ ke titik $(4,2)$. Jika transformasi yang sama memetakan titik $(x,y)$ ke titik $(12,6)$, maka nilai $x-y$ adalah …
A. -9
B. -3
C. 0
D. 3
E. 9
Pembahasan:
$\left( \begin{matrix} 0 & a \\ b & 0 \\ \end{matrix} \right)\left( \begin{matrix} 1 \\ 2 \\ \end{matrix} \right)=\left( \begin{matrix} 4 \\ 2 \\ \end{matrix} \right)$
$\left( \begin{matrix} 2a \\ b \\ \end{matrix} \right)=\left( \begin{matrix} 4 \\ 2 \\ \end{matrix} \right)\Leftrightarrow a=2,b=2$
$A=\left( \begin{matrix} 0 & 2 \\ 2 & 0 \\ \end{matrix} \right)$
Sehingga:
$\left( \begin{matrix} 0 & 2 \\ 2 & 0 \\ \end{matrix} \right)\left( \begin{matrix} x \\ y \\ \end{matrix} \right)=\left( \begin{matrix} 12 \\ 6 \\ \end{matrix} \right)$
$\left( \begin{matrix} 2y \\ 2x \\ \end{matrix} \right)=\left( \begin{matrix} 12 \\ 6 \\ \end{matrix} \right)$
$2y=12\Leftrightarrow y=6$
$2x=6\Leftrightarrow x=3$
Nilai $x-y=3-6=-3$
Jawaban: B
Matematika Dasar SBMPTN 2017 No. 58
$\int{\sqrt{x}\left( {{x}^{2}}-\frac{1}{{{x}^{2}}} \right)dx}$ = …
A. $\frac{2}{7}{{x}^{3}}\sqrt{x}+\frac{2}{\sqrt{x}}+c$
B. $\frac{2}{7}{{x}^{3}}\sqrt{x}+\frac{1}{\sqrt{x}}+c$
C. $\frac{2}{7}{{x}^{3}}\sqrt{x}+\frac{1}{2\sqrt{x}}+c$
D. $\frac{2}{7}{{x}^{3}}\sqrt{x}-\frac{2}{\sqrt{x}}+c$
E. $\frac{2}{7}{{x}^{3}}\sqrt{x}-\frac{1}{2\sqrt{x}}+c$
Pembahasan:
$\int{\sqrt{x}\left( {{x}^{2}}-\frac{1}{{{x}^{2}}} \right)dx}$
= $\int{{{x}^{\frac{1}{2}}}\left( {{x}^{2}}-{{x}^{-2}} \right)dx}$
= $\int{\left( {{x}^{\frac{5}{2}}}-{{x}^{\frac{-3}{2}}} \right)dx}$
= $\frac{2}{7}{{x}^{\frac{7}{2}}}+2{{x}^{\frac{-1}{2}}}+c$
= $\frac{2}{7}{{x}^{2}}\sqrt{x}+\frac{2}{\sqrt{x}}+c$
Jawaban: A
Matematika Dasar SBMPTN 2017 No. 59
Jika kurva $f(x)=a{{x}^{2}}+bx+c$ memotong sumbu-y di titik $(0,1)$ dan $\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)}{x-1}=-4$, maka $\frac{b+c}{a}$ = …
A. -1
B. $-\frac{1}{2}$
C. 0
D. 1
E. $\frac{3}{2}$
Pembahasan:
$(0,1)\to f(0)=a{{.0}^{2}}+b.0+c=1$ maka $c=1$ atau $f(x)=a{{x}^{2}}+bx+1$
Dari $\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)}{x-1}=-4$, maka $f(1)=0$
$f(1)=a{{.1}^{2}}+b.1+1=0$
$a+b+1=0$
$a+b=-1$
$\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)}{x-1}=-4$
$\underset{x\to 1}{\mathop{\lim }}\,\frac{a{{x}^{2}}+bx+1}{x-1}=-4$
Dengan Teorema L’Hospital
$\underset{x\to 1}{\mathop{\lim }}\,\frac{2ax+b}{1}=-4$
$2a+b=-4$
$a+b=-1$
-------------- (-)
$a=-3$ ,
$a+b=-1\Leftrightarrow -3+b=-1\Leftrightarrow b=2$
$\frac{b+c}{a}=\frac{2+1}{-3}=-1$
Jawaban: A
Matematika Dasar SBMPTN 2017 No. 60
Sebuah bilangan ganjil 5 angka diketahui memuat tepat 2 angka genap dan tidak memiliki angka berulang, serta tidak memuat angka 0. Banyak bilangan berbeda dengan ciri tersebut adalah …
A. 4.260
B. 4.290
C. 4.320
D. 5.400
E. 7.200
Pembahasan:
Langkah pertama:
Bilangan ganjil 5 angka, maka tersedia 5 kotak.

Untuk mengisi angka terakhir haruslah ganjil, sehingga ada 5 pilihan.
Langkah kedua:
Untuk mengisi 4 kotak pertama, karena tidak boleh memuat nol, tidak berulang, dan memuat tepat 2 angka genap, maka haruslah terdiri dari 2 pilihan angka genap (XX) dan 2 angka ganjil (YY), sehingga:

Susunan ${{X}_{1}}{{X}_{2}}{{Y}_{1}}{{Y}_{2}}$ ada sebanyak $\frac{4!}{2!.2!}=6$.
Langkah ketiga:
Kemudian untuk mengisi ${{X}_{1}}$ ada sebanyak 4 Pilihan, ${{X}_{2}}$ ada 3 pilihan, ${{Y}_{1}}$ ada 3 pilihan, dan ${{Y}_{2}}$ ada 3 pilihan. Jadi, total sebanyak $4\times 3\times 4\times 3=144$
Ada sebanyak 4 x 3 x 4 x 3 x 5 = 720 bilangan
Jadi, banyak bilangan yang dimaksud adalah: $5 \times 6 \times 144=4320$
Jawaban: C
Matematika Dasar SBMPTN 2017 No. 46
Misalkan ${{A}^{T}}$ adalah transpose matriks A dan $I=\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right)$. Jika $A=\left( \begin{matrix} a & b \\ 0 & 3 \\ \end{matrix} \right)$ sehingga $2A+3{{A}^{T}}=15I$, maka nilai ${{a}^{2}}+{{b}^{2}}$ adalah …
A. 2
B. 4
C. 5
D. 8
E. 9
Pembahasan:
$2A+3{{A}^{T}}=15I$
$2\left( \begin{matrix} a & b \\ 0 & 3 \\ \end{matrix} \right)+3\left( \begin{matrix} a & 0 \\ b & 3 \\ \end{matrix} \right)=15\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right)$
$\left( \begin{matrix} 2a & 2b \\ 0 & 6 \\ \end{matrix} \right)+\left( \begin{matrix} 3a & 0 \\ 3b & 9 \\ \end{matrix} \right)=\left( \begin{matrix} 15 & 0 \\ 0 & 15 \\ \end{matrix} \right)$
$\left( \begin{matrix} 5a & 2b \\ 3b & 15 \\ \end{matrix} \right)=\left( \begin{matrix} 15 & 0 \\ 0 & 15 \\ \end{matrix} \right)$
$5a=15\Leftrightarrow a=3$
$2b=0\Leftrightarrow b=0$
Nilai ${{a}^{2}}+{{b}^{2}}={{3}^{2}}+{{0}^{2}}=9$
Jawaban: E
Matematika Dasar SBMPTN 2017 No. 47
Jika himpunan penyelesaian $|2x-a| < 5$ adalah {$x|-1 < x < 4$}, maka nilai $a$ adalah …
A. -4
B. -3
C. -1
D. 3
E. 4
Pembahasan:
$|2x-a| < 5$
$-5 < 2x-a < 5$
$-5+a < 2x < 5+a$
$\frac{-5+a}{2} < x < \frac{5+a}{2}$ ekuivalen dengan $-1 < x < 4$, maka:
$\frac{5+a}{2}=4\Leftrightarrow 5+a=8\Leftrightarrow a=3$
Jawaban: D
Matematika Dasar SBMPTN 2017 No. 48

Pada segitiga siku-siku samakaki ABC, sisi AB dan BC masing-masing terbagi menjadi tiga bagian yang sama, berturut-turut oleh titik K, L, M, dan N. Jika luas segitiga ABC adalah $x$ $c{{m}^{2}}$, maka luas segitiga KMN adalah … $c{{m}^{2}}$.
A. $\frac{x}{3}$
B. $\frac{2x}{9}$
C. $\frac{x}{9}$
D. $\frac{x}{18}$
E. $\frac{x}{36}$
Pembahasan:
Perhatikan gambar.
Misalkan BC = AC = $y$
Sehingga luas ABC:
$\frac{1}{2}{{y}^{2}}=x$
BM = MN = NC = $\frac{1}{3}y$ serta BK = $\frac{2}{3}y$.
Luas segitiga KMN dengan alas = MN dan tinggi = BK adalah:
= $\frac{1}{2}.\frac{1}{3}y.\frac{2}{3}y=\frac{2}{9}.\frac{1}{2}{{y}^{2}}$
= $\frac{2}{9}.\frac{1}{2}{{y}^{2}}$
= $\frac{2}{9}.x=\frac{2x}{9}$
Jawaban: B
Matematika Dasar SBMPTN 2017 No. 49
Jika $f(x)=\sqrt{x-1}$ dan $g(x)=\frac{x-5}{x-1}$, $x\ne 1$, maka daerah asal $f.g$ adalah …
A. $-\infty < x < \infty $
B. $x\ne 0$
C. $x\ne 1$
D. $x\ge 1$
E. $x > 1$
Pembahasan:
$f.g=\sqrt{x-1}.\frac{x-5}{x-1}$
$f.g=\frac{(x-5)\sqrt{x-1}}{x-1}$
Daerah asal $f.g$ yaitu:
i) syarat bentuk akar $\sqrt{x-1}$ adalah $x-1\ge 0\Leftrightarrow x\ge 1$
ii) syarat penyebut $x-1\ne 0\Leftrightarrow x\ne 1$
dari i) dan ii) diperoleh:
Daerah asal $f.g$ adalah $x > 1$
Jawaban: E
Matematika Dasar SBMPTN 2017 No. 50
Diketahui median dan rata-rata berat badan 5 balita adalah sama. Setelah ditambahkan satu data berat badan balita, rata-ratanya meningkat 1 kg, sedangkan mediannya tetap. Jika 6 data berat badan tersebut diurutkan dari yang paling ringan ke yang paling berat, maka selisih berat badan antara balita terakhir yang ditambahkan dan balita di urutan ke-4 adalah … kg.
A. 4
B. $\frac{9}{2}$
C. 5
D. 6
E. $\frac{13}{2}$
Pembahasan:
Setelah diurutkan berat badan kelima balita itu adalah:
$a$, $b$, $c$, $d$, $e$
$Me=c=\bar{x}$
$\bar{x}=\frac{a+b+c+d+e}{5}=c$, maka:
$a+b+c+d+e=5c$.
Jika ditambah data berat badan seorang balita lagi, misalkan $f$, maka rata-ratanya naik 1 dan mediannya tetap, artinya:
*) karena rata-rata mengalami kenaikan maka dapatlah disimpulkan bahwa $f$ data terbesar.
*) $a$, $b$, $c$, $d$, $e$, $f$
$Me=c$, maka $d=c$
*) rata-rata menjadi:
$\frac{a+b+c+d+e+f}{6}=c+1$
$\frac{5c+f}{6}=c+1$
$5c+f=6c+6$
$f-c=6$
Selisih berat badan balita ke-6 ($f$) dengan balita urutan ke-4 ($d$) adalah:
$f-d=f-c=6$
Jawaban: D
Matematika Dasar SBMPTN 2017 No. 51
Jumlah suku ke-3 dan ke-7 suatu barisan aritmetika dengan suku-sukunya bilangan asli adalah 28. Jika beda barisan tersebut 3, maka suku ke-7 adalah …
A. 19
B. 20
C. 21
D. 22
E. 23
Pembahasan:
Barisan Aritmetika: ${{U}_{n}}=a+(n-1)b$
${{U}_{3}}+{{U}_{7}}=28$
$(a+2b)+(a+6b)=28$
$2a+8b=28$
$a+4b=14$; $b=3$
$a+4.3=14\Leftrightarrow a=2$
${{U}_{7}}=a+6b=2+6.3=20$
Jawaban: B
Matematika Dasar SBMPTN 2017 No. 52
Seseorang memelihara ikan di suatu kolam. Rata-rata bobot ikan per ekor pada saat panen dari kolam tersebut adalah $(6-0,02x)$ kg, dengan $x$ menyatakan banyak ikan yang dipelihara. Maksimum total bobot semua ikan pada saat panen yang mungkin adalah … kg.
A. 400
B. 420
C. 435
D. 450
E. 465
Pembahasan:
Total bobot semua ikan adalah:
$f(x)=(6-0,02x)x=6x-0,02{{x}^{2}}$.
Agar total maksimum, maka $f'(x)=0$
$f(x)=6x-0,02{{x}^{2}}$
$f'(x)=6-0,04x=0$
$0,04x=6\Leftrightarrow x=\frac{6}{0,04}=150$
$f(150)=(6-0,02.(150)).150$
$f(150)=(6-3).150=450$
Maka total bobot maksimum adalah 450 kg.
Jawaban: D
Matematika Dasar SBMPTN 2017 No. 53
Lima bilangan asli membentuk barisan geometri dengan rasio positif. Jika jumlah 3 suku terbesar dan jumlah 3 suku terkecil barisan geometri berturut-turut adalah 171 dan 76, maka jumlah 5 bilangan tersebut adalah …
A. 125
B. 130
C. 180
D. 211
E. 347
Pembahasan:
Barisan Geometri: ${{U}_{n}}=a{{r}^{n-1}}$,
${{U}_{1}},{{U}_{2}},{{U}_{3}},{{U}_{4}},{{U}_{5}}$ $r > 0$
Jumlah 3 suku terbesar adalah 171, maka:
${{U}_{3}}+{{U}_{4}}+{{U}_{5}}=171$
$a{{r}^{2}}+a{{r}^{3}}+a{{r}^{4}}=171$
$a{{r}^{2}}(1+r+{{r}^{2}})=171$ …. Persamaan (1)
Jumlah 3 suku terbesar adalah 76, maka:
${{U}_{1}}+{{U}_{2}}+{{U}_{3}}=76$
$a+ar+a{{r}^{2}}=76$
$a(1+r+{{r}^{2}})=76$ …. Persamaan (2)
Persamaan (1) dibagi dengan persamaan (2), maka:
$\frac{a{{r}^{2}}(1+r+{{r}^{2}})}{a(1+r+{{r}^{2}})}=\frac{171}{76}$
${{r}^{2}}=\frac{9}{4}\Leftrightarrow r=\frac{3}{2}$
Substitusi ke persamaan (2):
$a(1+r+{{r}^{2}})=76$
$a\left( 1+\frac{3}{2}+{{\left( \frac{3}{2} \right)}^{2}} \right)=76$
$a\left( 1+\frac{3}{2}+\frac{9}{4} \right)=76$
$\frac{19}{4}a=76\Leftrightarrow a=16$
${{S}_{n}}=\frac{a({{r}^{n}}-1)}{r-1}$
${{S}_{5}}=\frac{16\left( {{\left( \frac{3}{2} \right)}^{5}}-1 \right)}{\frac{3}{2}-1}$
${{S}_{5}}=\frac{16\left( \frac{243}{32}-1 \right)}{\frac{1}{2}}$
${{S}_{5}}=32.\frac{211}{32}=211$
Jawaban: D
Matematika Dasar SBMPTN 2017 No. 54
Jika $f(x)={{x}^{2}}+2$ dan $g(x)=-3x+8$, maka nilai maksimum fungsi $(g\circ f)(x)$ adalah …
A. 0
B. 1
C. 2
D. 3
E. 4
Pembahasan:
$\begin{align} (g\circ f)(x) &=g(f(x)) \\ &=g({{x}^{2}}+2) \\ & =-3({{x}^{2}}+2)+8 \\ (g\circ f)(x) &=-3{{x}^{2}}+2
\end{align}$
Nilai maksimum diperoleh jika:
$(g\circ f)'(x)=0$
$-6x=0\Leftrightarrow x=0$
$(g\circ f)(x)=-3{{x}^{2}}+2$
$(g\circ f)(0)=-{{3.0}^{2}}+2=2$
Jawaban: C
Matematika Dasar SBMPTN 2017 No. 55
Diketahui kubus ABCD.EFGH dengan titik P terletak pada perpanjangan BF sehingga FP = 3 cm dan garis AP berpotongan dengan garis EF di titik Q. Jika panjang rusuk kubus tersebut adalah 6 cm, maka jarak Q ke D adalah … cm.
A. $2\sqrt{13}$
B. $2\sqrt{18}$
C. $2\sqrt{22}$
D. $4\sqrt{7}$
E. $4\sqrt{11}$
Pembahasan:
Perhatikan gambar berikut!


Segitiga ABP sebangun dengan segitiga QFP, maka berlaku:
$\frac{x}{6}=\frac{3}{3+6}\Leftrightarrow \frac{x}{6}=\frac{3}{9}\Leftrightarrow x=2$
Karena $QF=x=2$, maka $EQ=6-2=4$ sehingga:
$A{{Q}^{2}}=E{{Q}^{2}}+E{{A}^{2}}$
$A{{Q}^{2}}={{4}^{2}}+{{6}^{2}}=52$
Perhatikan segitiga DAQ siku-siku di A, maka:
$\begin{align} DQ &= \sqrt{D{{A}^{2}}+A{{Q}^{2}}} \\ & =\sqrt{{{6}^{2}}+52} \\ & =\sqrt{88} \\ DQ &=2\sqrt{22} \end{align}$
Jawaban: C
Matematika Dasar SBMPTN 2017 No. 56
Luas daerah penyelesaian sistem pertidaksamaan $y+4x\le 12$, $y+2x\ge 8$, $x\ge 0$ adalah … satuan luas.
A. 2
B. 4
C. 6
D. 8
E. 10
Pembahasan:
Derah penyelesaian dari sistem pertidaksamaan tersebut adalah daerah yang diarsir pada gambar berikut!

Derah yang diarsir merupakan segitiga yang alasnya $a=12-8=4$ dan tingginya $t=2$.
Jadi, luasnya adalah:
L = $\frac{1}{2}.a.t$
L = $\frac{1}{2}.4.2=4$
Jawaban: B
Matematika Dasar SBMPTN 2017 No. 57
Transformasi yang bersesuaian dengan matriks $A=\left( \begin{matrix} 0 & a \\ b & 0 \\ \end{matrix} \right)$ memetakan titik $(1,2)$ ke titik $(4,2)$. Jika transformasi yang sama memetakan titik $(x,y)$ ke titik $(12,6)$, maka nilai $x-y$ adalah …
A. -9
B. -3
C. 0
D. 3
E. 9
Pembahasan:
$\left( \begin{matrix} 0 & a \\ b & 0 \\ \end{matrix} \right)\left( \begin{matrix} 1 \\ 2 \\ \end{matrix} \right)=\left( \begin{matrix} 4 \\ 2 \\ \end{matrix} \right)$
$\left( \begin{matrix} 2a \\ b \\ \end{matrix} \right)=\left( \begin{matrix} 4 \\ 2 \\ \end{matrix} \right)\Leftrightarrow a=2,b=2$
$A=\left( \begin{matrix} 0 & 2 \\ 2 & 0 \\ \end{matrix} \right)$
Sehingga:
$\left( \begin{matrix} 0 & 2 \\ 2 & 0 \\ \end{matrix} \right)\left( \begin{matrix} x \\ y \\ \end{matrix} \right)=\left( \begin{matrix} 12 \\ 6 \\ \end{matrix} \right)$
$\left( \begin{matrix} 2y \\ 2x \\ \end{matrix} \right)=\left( \begin{matrix} 12 \\ 6 \\ \end{matrix} \right)$
$2y=12\Leftrightarrow y=6$
$2x=6\Leftrightarrow x=3$
Nilai $x-y=3-6=-3$
Jawaban: B
Matematika Dasar SBMPTN 2017 No. 58
$\int{\sqrt{x}\left( {{x}^{2}}-\frac{1}{{{x}^{2}}} \right)dx}$ = …
A. $\frac{2}{7}{{x}^{3}}\sqrt{x}+\frac{2}{\sqrt{x}}+c$
B. $\frac{2}{7}{{x}^{3}}\sqrt{x}+\frac{1}{\sqrt{x}}+c$
C. $\frac{2}{7}{{x}^{3}}\sqrt{x}+\frac{1}{2\sqrt{x}}+c$
D. $\frac{2}{7}{{x}^{3}}\sqrt{x}-\frac{2}{\sqrt{x}}+c$
E. $\frac{2}{7}{{x}^{3}}\sqrt{x}-\frac{1}{2\sqrt{x}}+c$
Pembahasan:
$\int{\sqrt{x}\left( {{x}^{2}}-\frac{1}{{{x}^{2}}} \right)dx}$
= $\int{{{x}^{\frac{1}{2}}}\left( {{x}^{2}}-{{x}^{-2}} \right)dx}$
= $\int{\left( {{x}^{\frac{5}{2}}}-{{x}^{\frac{-3}{2}}} \right)dx}$
= $\frac{2}{7}{{x}^{\frac{7}{2}}}+2{{x}^{\frac{-1}{2}}}+c$
= $\frac{2}{7}{{x}^{2}}\sqrt{x}+\frac{2}{\sqrt{x}}+c$
Jawaban: A
Matematika Dasar SBMPTN 2017 No. 59
Jika kurva $f(x)=a{{x}^{2}}+bx+c$ memotong sumbu-y di titik $(0,1)$ dan $\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)}{x-1}=-4$, maka $\frac{b+c}{a}$ = …
A. -1
B. $-\frac{1}{2}$
C. 0
D. 1
E. $\frac{3}{2}$
Pembahasan:
$(0,1)\to f(0)=a{{.0}^{2}}+b.0+c=1$ maka $c=1$ atau $f(x)=a{{x}^{2}}+bx+1$
Dari $\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)}{x-1}=-4$, maka $f(1)=0$
$f(1)=a{{.1}^{2}}+b.1+1=0$
$a+b+1=0$
$a+b=-1$
$\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)}{x-1}=-4$
$\underset{x\to 1}{\mathop{\lim }}\,\frac{a{{x}^{2}}+bx+1}{x-1}=-4$
Dengan Teorema L’Hospital
$\underset{x\to 1}{\mathop{\lim }}\,\frac{2ax+b}{1}=-4$
$2a+b=-4$
$a+b=-1$
-------------- (-)
$a=-3$ ,
$a+b=-1\Leftrightarrow -3+b=-1\Leftrightarrow b=2$
$\frac{b+c}{a}=\frac{2+1}{-3}=-1$
Jawaban: A
Matematika Dasar SBMPTN 2017 No. 60
Sebuah bilangan ganjil 5 angka diketahui memuat tepat 2 angka genap dan tidak memiliki angka berulang, serta tidak memuat angka 0. Banyak bilangan berbeda dengan ciri tersebut adalah …
A. 4.260
B. 4.290
C. 4.320
D. 5.400
E. 7.200
Pembahasan:
Langkah pertama:
Bilangan ganjil 5 angka, maka tersedia 5 kotak.

Untuk mengisi angka terakhir haruslah ganjil, sehingga ada 5 pilihan.
Langkah kedua:
Untuk mengisi 4 kotak pertama, karena tidak boleh memuat nol, tidak berulang, dan memuat tepat 2 angka genap, maka haruslah terdiri dari 2 pilihan angka genap (XX) dan 2 angka ganjil (YY), sehingga:

Susunan ${{X}_{1}}{{X}_{2}}{{Y}_{1}}{{Y}_{2}}$ ada sebanyak $\frac{4!}{2!.2!}=6$.
Langkah ketiga:
Kemudian untuk mengisi ${{X}_{1}}$ ada sebanyak 4 Pilihan, ${{X}_{2}}$ ada 3 pilihan, ${{Y}_{1}}$ ada 3 pilihan, dan ${{Y}_{2}}$ ada 3 pilihan. Jadi, total sebanyak $4\times 3\times 4\times 3=144$
Ada sebanyak 4 x 3 x 4 x 3 x 5 = 720 bilangan
Jadi, banyak bilangan yang dimaksud adalah: $5 \times 6 \times 144=4320$
Jawaban: C
Artikel Terkait:
|

Post a Comment for "Pembahasan SBMPTN 2017 Matematika Dasar Kode 232"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.