Pembahasan SBMTPN 2016 TKPA (Matematika Dasar)
Berikut ini adalah pembahasan TKPA (Matematika Dasar) SBMPTN 2016 dengan kode soal 317. Catatan Matematika selalu membagikan soal di awal postingan untuk dapat dipelajari terlebih dahulu secara mandiri dan soal tersebut dapat didownload dan linknya tersedia di bawah ini. Setelah soal didownload cobalah adik-adik pejuang PTN menjawabnya, setelah itu bolehlah melirik dan mempelajari pembahasannya disini.
Matematika Dasar SBMPTN 2016 No. 46
Misalkan dua persamaan kuadrat mempunyai satu akar yang sama, yaitu 2 dan akar-akar lainnya berkebalikan. Jika salah satu persamaan itu adalah ${{x}^{2}}-ax+6=0$, maka persamaan kuadrat lainnya adalah …
A. ${{x}^{2}}+x-6=0$
B. $3{{x}^{2}}-7x+2=0$
C. $3{{x}^{2}}+4x-6=0$
D. ${{x}^{2}}-x+\frac{2}{3}=0$
E. $2{{x}^{2}}-3x-4=0$
Pembahasan:
Persamaan kuadrat 1.
${{x}^{2}}-ax+6=0$, akar-akarnya ${{x}_{1}}$ dan ${{x}_{2}}$, diketahui ${{x}_{1}}=2$, maka:
${{x}_{1}}.{{x}_{2}}=6\Leftrightarrow 2.{{x}_{2}}=6\Leftrightarrow {{x}_{2}}=3$
${{x}_{1}}+{{x}_{2}}=a\Leftrightarrow 2+3=a\Leftrightarrow a=5$
Persamaan kuadrat 2.
Akar-akarnya ${{x}_{3}}={{x}_{1}}=2$ dan ${{x}_{4}}=\frac{1}{{{x}_{2}}}=\frac{1}{3}$, maka:
$(x-{{x}_{3}})(x-{{x}_{4}})=0$
$(x-2)(x-\frac{1}{3})=0$, kalikan dengan 3, maka:
$(x-2)(3x-1)=0$
$3{{x}^{2}}-7x+2=0$
Jawaban: B
Matematika Dasar SBMPTN 2016 No. 47
Jika ${{A}^{2x}}=2$, maka $\frac{{{A}^{5x}}-{{A}^{-5x}}}{{{A}^{3x}}+{{A}^{-3x}}}$ = …
A. $\frac{31}{18}$
B. $\frac{31}{9}$
C. $\frac{32}{18}$
D. $\frac{33}{9}$
E. $\frac{33}{18}$
Pembahasan:
$\frac{{{A}^{5x}}-{{A}^{-5x}}}{{{A}^{3x}}+{{A}^{-3x}}}$
= $\frac{{{A}^{5x}}-{{A}^{-5x}}}{{{A}^{3x}}+{{A}^{-3x}}}\times \frac{{{A}^{5x}}}{{{A}^{5x}}}$
= $\frac{{{A}^{10x}}-1}{{{A}^{8x}}+{{A}^{2x}}}$
= $\frac{{{\left( {{A}^{2x}} \right)}^{5}}-1}{{{\left( {{A}^{2x}} \right)}^{4}}+{{A}^{2x}}}$
= $\frac{{{2}^{5}}-1}{{{2}^{4}}+2}=\frac{31}{18}$
Jawaban: A
Matematika Dasar SBMPTN 2016 No. 48
Suatu garis yang melalui titik $(0,0)$ membagi persegipanjang dengan titik-titik sudut $(1,0)$, $(5,0)$, $(1,12)$ dan $(5,12)$ menjadi dua bagian yang sama luas. Gradien garis tersebut adalah …
A. $\frac{1}{2}$
B. 1
C. 2
D. $\frac{12}{5}$
E. 3
Pembahasan:
Perhatikan gambar berikut!
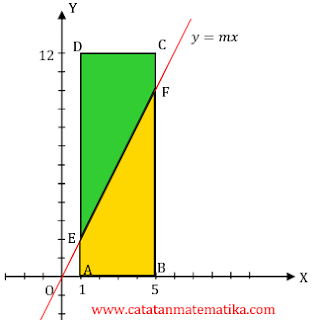
Titik E dan F terletak pada garis $y=mx$ yang masing-masing absisnya adalah 1 dan 5, sehingga:
$x=1\to y=mx\Leftrightarrow y=m\Leftrightarrow E(1,m)$
$x=5\to y=mx\Leftrightarrow y=5m\Leftrightarrow E(1,5m)$
Panjang AE = m dan BF = 5m
Luas ABCD = 4 x 12 = 48
Karena garis $y=mx$ membagi dua ABCD menjadi dua bagian yang sama luasnya, maka:
Luas ABFE = $\frac{1}{2}$x Luas ABCD
$\frac{(AE+BF).AB}{2}=\frac{1}{2}\times 48$
$\frac{(m+5m).4}{2}=24$
$24m=48$
$m=2$
Jawaban: C
Matematika Dasar SBMPTN 2016 No. 49
Semua bilangan real $x$ yang memenuhi $\frac{x}{2-x} > \frac{2+x}{x}$ adalah …
A. $-\sqrt{2} < x < 0$ atau $\sqrt{2} < x < 2$
B. $x < -\sqrt{2}$ atau $0 < x < \sqrt{2}$
C. $x < -\sqrt{2}$ atau $x > 2$
D. $x < -\sqrt{2}$ atau $x > \sqrt{2}$
E. $0 < x < 2$
Pembahasan:
$\frac{x}{2-x} > \frac{2+x}{x}$
$\frac{x}{2-x}-\frac{2+x}{x} > 0$
$\frac{{{x}^{2}}}{(2-x)x}-\frac{(2+x)(2-x)}{(2-x)x} > 0$
$\frac{{{x}^{2}}}{(2-x)x}-\frac{4-{{x}^{2}}}{(2-x)x} > 0$
$\frac{2{{x}^{2}}-4}{(2-x)x} > 0$
$\frac{{{x}^{2}}-2}{(2-x)x} > 0$
$\frac{(x-\sqrt{2})(x+\sqrt{2})}{(2-x)x} > 0$
$x=\sqrt{2}$, $x=-\sqrt{2}$, $x\ne 2$, $x\ne 0$
Uji garis bilangan:

HP = {$-\sqrt{2} < x < 0$ atau $\sqrt{2} < x < 2$}
Jawaban: A
Matematika Dasar SBMPTN 2016 No. 50
Jika grafik fungsi $y={{x}^{2}}-(9+a)x+9a$ diperoleh dari grafik fungsi $y={{x}^{2}}-2x-3$ melalui pencerminan terhadap garis $x=4$ maka $a$ = …
A. 7
B. 5
C. 3
D. -5
E. -7
Pembahasan:
$y={{x}^{2}}-2x-3$ dicerminkan terhadap garis $x=4$
$P(x,y)$ dicerminkan terhadap garis $x=4$, menghasilkan bayangan
$P'(x',y')=P'(2.4-x,y)=P'(8-x,y)$
$8-x=x'\Leftrightarrow x=8-x'$ dan $y=y'$ substitusikan ke:
$y={{x}^{2}}-2x-3$
$y'={{(8-x')}^{2}}-2(8-x')-3$
$y=64-16x+{{x}^{2}}-16+2x-3$
$y={{x}^{2}}-14x+45$,
Pada soal bayangan $y={{x}^{2}}-2x-3$ adalah $y={{x}^{2}}-(9+a)x+9a$, maka:
${{x}^{2}}-(9+a)x+9a\equiv {{x}^{2}}-14x+45$
$9a=45\Leftrightarrow a=5$
Jawaban: B
Matematika Dasar SBMPTN 2016 No. 51
Tujuh finalis lomba menyanyi tingkat SMA disuatu kota berasal dari 6 SMA yang berbeda terdiri atas empat pria dan tiga wanita. Diketahui satu pria dan satu wanita berasal dari SMA “A”. Jika urutan tampil diatur bergantian antara pria dan wanita, serta finalis dari SMA “A” tidak tampil berurutan, maka susunan urutan tampil yang mungkin ada sebanyak …
A. 144
B. 108
C. 72
D. 36
E. 35
Pembahasan:
Misalkan: P = Pria, W = Wanita
Susunan yang mungkin agar pria wanita tampil bergantian adalah:
PWPWPWP ada sebanyak 4! x 3! = 144
Misalkan ${{P}_{A}}$ dan ${{W}_{A}}$ menyatakan siswa dari SMA “A” maka susunan siswa SMA “A” tampil berurutan adalah:
${{P}_{A}}{{W}_{A}}PWPWP$ ada sebanyak 3! x 2! = 12
$P{{W}_{A}}{{P}_{A}}WPWP$ ada sebanyak 3! x 2! = 12
$PW{{P}_{A}}{{W}_{A}}PWP$ ada sebanyak 3! x 2! = 12
$PWP{{W}_{A}}{{P}_{A}}WP$ ada sebanyak 3! x 2! = 12
$PWPW{{P}_{A}}{{W}_{A}}P$ ada sebanyak 3! x 2! = 12
$PWPWP{{W}_{A}}{{P}_{A}}$ ada sebanyak 3! x 2! = 12
Seluruhnya ada sebanyak = 6 x 12 = 72
Jadi, susunan urutan tampil diatur bergantian antara pria dan wanita, serta finalis dari SMA “A” tidak tampil berurutan ada sebanyak = 144 – 72 = 72.
Jawaban: C
Matematika Dasar SBMPTN 2016 No. 52
Jika tabel berikut menyatakan hasil fungsi f dan g
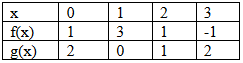
Maka $(f\circ g\circ f)(1)+(g\circ f\circ g)(2)$ = …
A. -1
B. 1
C. 2
D. 3
E. 5
Pembahasan:
$(f\circ g\circ f)(1)+(g\circ f\circ g)(2)$
= $f(g(f(1)))+g(f(g(2)))$
= $f(g(3))+g(f(1))$
= $f(2)+g(3)$
= $1+2=3$
Jawaban: D
Matematika Dasar SBMPTN 2016 No. 53
Jika fungsi $f$ dan $g$ mempunyai invers dan memenuhi $f(2x)=g(x+3)$, maka ${{f}^{-1}}(x)$ = …
A. ${{g}^{-1}}\left( \frac{x}{2}-\frac{3}{2} \right)$
B. ${{g}^{-1}}(2x-6)$
C. $2{{g}^{-1}}(x)-3$
D. $2{{g}^{-1}}(x)-6$
E. $2{{g}^{-1}}(x)+6$
Pembahasan:
$f(2x)=g(x+3)$
${{f}^{-1}}(g(x+3))=2x$
$({{f}^{-1}}\circ g)(x+3)=2x$
$({{f}^{-1}}\circ g)(x)=2(x-3)$
$({{f}^{-1}}\circ g)(x)=2x-6$
${{f}^{-1}}(g(x))=2x-6$
${{f}^{-1}}(x)=2{{g}^{-1}}(x)-6$
Jawaban: D
Matematika Dasar SBMPTN 2016 No. 54
Diketahui matriks $A=\left( \begin{matrix} 8 & a \\ a & 1 \\ \end{matrix} \right)$, $B=\left( \begin{matrix} 1 & -1 \\ b & 1 \\ \end{matrix} \right)$, dan C adalah matriks berukuran 2x2 yang mempunyai invers. Jika AC dan BC tidak memiliki invers, maka $3{{a}^{2}}+4{{b}^{3}}$ = …
A. 16
B. 20
C. 24
D. 28
E. 36
Pembahasan:
AC tidak memiliki invers, maka det(AC) = 0
$|AC|=0$
$|A||C|=0$, karena C mempunyai invers, maka:
det(A) = 0
$8-{{a}^{2}}=0\Leftrightarrow {{a}^{2}}=8$
BC tidak memiliki invers, maka det(BC) = 0
$|BC|=0$
$|B||C|=0$, karena C mempunyai invers, maka:
det(B) = 0
$\left| \begin{matrix} 1 & -1 \\ b & 1 \\ \end{matrix} \right|=0\Leftrightarrow 1+b=0\Leftrightarrow b=-1$
$3{{a}^{2}}+4{{b}^{3}}=3.8+{{4.1}^{3}}=28$
Jawaban: D
Matematika Dasar SBMPTN 2016 No. 55
Misalkan ${{U}_{k}}$ dan ${{S}_{k}}$ berturut-turut menyatakan suku ke-k dan jumlah k suku pertama suatu barisan aritmetika. Jika ${{U}_{2}}-{{U}_{4}}$ + ${{U}_{6}}-{{U}_{8}}$ + ${{U}_{10}}-{{U}_{12}}$ + ${{U}_{14}}-{{U}_{16}}$ + ${{U}_{18}}=20$, maka ${{S}_{19}}$ = …
A. 630
B. 380
C. 210
D. 105
E. 21
Pembahasan:
${{U}_{2}}-{{U}_{4}}$ + ${{U}_{6}}-{{U}_{8}}$ + ${{U}_{10}}-{{U}_{12}}$ + ${{U}_{14}}-{{U}_{16}}$ + ${{U}_{18}}=20$
$(a+b)-(a+3b)$ + $(a+5b)-(a+7b)$ + $(a+9b)-(a+11b)$ + $(a+13b)-(a+15b)$ + $(a+17b)=20$
$a+9b=20$
${{S}_{19}}=\frac{19}{2}(2a+18b)$
${{S}_{19}}=19(a+9b)$
${{S}_{19}}=19.20=380$
Jawaban: B
Matematika Dasar SBMPTN 2016 No. 56

Diketahui semua titik sudut segienam beraturan ABCDEF terletak pada lingkaran yang berjari-jari 2 cm seperti pada gambar. Luas daerah yang tidak diarsir pada segienam tersebut adalah … cm$^2$.
A. 3
B. $2\sqrt{3}$
C. 4
D. $3\sqrt{3}$
E. $6\sqrt{3}$
Pembahasan:
Perhatikan gambar berikut!

Karena ABCDEF adalah segienam berarutan, maka dengan jari-jari 2 cm, maka OA = OB = OC = OD = OE = OF = AB = BC = CD = DE = EF = AF, sehingga:
Segitiga ABO adalah segitiga sama sisi dengan panjang sisi 2 cm.
Pada segitiga AQO berlaku pythagoras, yaitu:
$A{{Q}^{2}}=O{{A}^{2}}-O{{Q}^{2}}$
${{t}^{2}}={{2}^{2}}-{{1}^{2}}$
$t=\sqrt{3}$
Luas ABO + Luas OEF adalah
= $\frac{1}{2}.AP.t+\frac{1}{2}.PF.t$
= $\frac{1}{2}t(AP+PF)$
= $\frac{1}{2}\sqrt{3}.2$
= $\sqrt{3}$
Luas PCD adalah:
= $\frac{1}{2}.CD.2t$
= $\frac{1}{2}.2.2\sqrt{3}$
= $2\sqrt{3}$
Luas arsiran adalah:
= Luas ABO + Luas OEF + Luas PCD
= $\sqrt{3}+2\sqrt{3}=3\sqrt{3}$
Jawaban: D
Matematika Dasar SBMPTN 2016 No. 57
Nilai ujian matematika 30 siswa pada suatu kelas berupa bilangan cacah tidak lebih daripada 10. Rata-rata nilai mereka adalah 8 dan hanya terdapat 5 siswa yang memperoleh nilai 7. Jika $p$ menyatakan banyak siswa yang memperoleh nilai kurang dari 7, maka nilai $p$ terbesar yang mungkin adalah …
A. 5
B. 7
C. 9
D. 11
E. 14
Pembahasan:
$\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+...+{{x}_{30}}}{30}=8$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+...+{{x}_{30}}=240$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+...+{{x}_{25}}+5.7=240$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+...+{{x}_{25}}=205$
Agar $p$ maksimal maka siswa bernilai 6 $p$ dan sisanya bernilai maksimal yaitu sebanyak $(25-p)$ bernilai 10, sehingga:
$6p+(25-p).10\le 205$
$-4p+250\le 205$
$-4p\le -45\Leftrightarrow p\le 11,25$
Karena $p$ bilangan asli maka $p$ terbesar adalah 11.
Jawaban: D
Matematika Dasar SBMPTN 2016 No. 58
Jika $a$ dan $b$ bilangan bulat, serta $\underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}-x-b}{2-x}=a$, maka $b-a$ = …
A. -5
B. -3
C. -1
D. 2
E. 5
Pembahasan:
$\underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}-x-b}{2-x}=a$
Jika $x=2$, maka:
${{x}^{2}}-x-b=0$
${{2}^{2}}-2-b=0\Leftrightarrow b=2$
$\underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}-x-2}{2-x}=a$
$\underset{x\to 2}{\mathop{\lim }}\,\frac{(x-2)(x+1)}{-(x-2)}=a$
$\underset{x\to 2}{\mathop{\lim }}\,-(x+1)=a$
$-(2+1)=a\Leftrightarrow a=-3$
maka nilai $b-a=2-(-3)=5$
Jawaban: E
Matematika Dasar SBMPTN 2016 No. 59
Jika $(x,y)=(1,3)$ dan $(x,y)=(a,1)$ merupakan penyelesaian $x-2y=b$ dan $cx+dy=10$, maka $a+b+c+d$ = …
A. -9
B. -6
C. 0
D. 3
E. 9
Pembahasan:
$x-2y=b$
$cx+dy=10$
Disusun dalam bentuk matriks menjadi:
$\left( \begin{matrix} 1 & -2 \\ c & d \\ \end{matrix} \right)\left( \begin{matrix} x \\ y \\ \end{matrix} \right)=\left( \begin{matrix} b \\ 10 \\ \end{matrix} \right)$
Karena $(x,y)=(1,3)$ dan $(x,y)=(a,1)$, maka:
$\left( \begin{matrix} 1 & -2 \\ c & d \\ \end{matrix} \right)\left( \begin{matrix} 1 & a \\ 3 & 1 \\ \end{matrix} \right)=\left( \begin{matrix} b & b \\ 10 & 10 \\ \end{matrix} \right)$
$\left( \begin{matrix} -5 & a-2 \\ c+3d & ac+d \\ \end{matrix} \right)=\left( \begin{matrix} b & b \\ 10 & 10 \\ \end{matrix} \right)$
$b=-5$
$a-2=b$
$a-2=-5\Leftrightarrow a=-3$
$c+3d=10\Leftrightarrow c=10-3d$
$ac+d=10$
$-3(10-3d)+d=10$
$-30+9d+d=10$
$10d=40\Leftrightarrow d=4$
$c=10-3d\Leftrightarrow c=10-3.4=-2$
$a+b+c+d=-3+(-5)+(-2)+4=-6$
Jawaban: B
Matematika Dasar SBMPTN 2016 No. 60
Semua bilangan real $x$ yang memenuhi $|x-2| > {{x}^{2}}-4$ adalah …
A. $x < -2$ atau $x > 3$
B. $x < -2$ atau $x > 2$
C. $x < -2$ atau $x > 0$
D. $-2 < x < 3$
E. $-3 < x < 2$
Pembahasan:
Sesuai definisi nilai mutlak:
$|x-2|=x-2$ jika $x-2\ge 0 \Leftrightarrow x\ge 2$
$|x-2|=-x+2$ jika $x-2 < 0 \Leftrightarrow x < 2$
a) Untuk $x\ge 2$ maka:
$|x-2| > {{x}^{2}}-4$
$x-2 > {{x}^{2}}-4$
$-{{x}^{2}}+x+2 > 0$
${{x}^{2}}-x-2 < 0$
$(x-2)(x+1) < 0$
$-1 < x < 2$ (tidak memenuhui syarat $x\ge 2$)
b) Untuk $x < 2$ maka:
$|x-2| > {{x}^{2}}-4$
$-x+2 > {{x}^{2}}-4$
$-{{x}^{2}}-x+6 > 0$
${{x}^{2}}+x-6 > 0$
$(x+3)(x-2) < 0$
$-3 < x < 2$ (memenuhui syarat)
HP: {$-3 < x < 2$}
Jawaban: E
Matematika Dasar SBMPTN 2016 No. 46
Misalkan dua persamaan kuadrat mempunyai satu akar yang sama, yaitu 2 dan akar-akar lainnya berkebalikan. Jika salah satu persamaan itu adalah ${{x}^{2}}-ax+6=0$, maka persamaan kuadrat lainnya adalah …
A. ${{x}^{2}}+x-6=0$
B. $3{{x}^{2}}-7x+2=0$
C. $3{{x}^{2}}+4x-6=0$
D. ${{x}^{2}}-x+\frac{2}{3}=0$
E. $2{{x}^{2}}-3x-4=0$
Pembahasan:
Persamaan kuadrat 1.
${{x}^{2}}-ax+6=0$, akar-akarnya ${{x}_{1}}$ dan ${{x}_{2}}$, diketahui ${{x}_{1}}=2$, maka:
${{x}_{1}}.{{x}_{2}}=6\Leftrightarrow 2.{{x}_{2}}=6\Leftrightarrow {{x}_{2}}=3$
${{x}_{1}}+{{x}_{2}}=a\Leftrightarrow 2+3=a\Leftrightarrow a=5$
Persamaan kuadrat 2.
Akar-akarnya ${{x}_{3}}={{x}_{1}}=2$ dan ${{x}_{4}}=\frac{1}{{{x}_{2}}}=\frac{1}{3}$, maka:
$(x-{{x}_{3}})(x-{{x}_{4}})=0$
$(x-2)(x-\frac{1}{3})=0$, kalikan dengan 3, maka:
$(x-2)(3x-1)=0$
$3{{x}^{2}}-7x+2=0$
Jawaban: B
Matematika Dasar SBMPTN 2016 No. 47
Jika ${{A}^{2x}}=2$, maka $\frac{{{A}^{5x}}-{{A}^{-5x}}}{{{A}^{3x}}+{{A}^{-3x}}}$ = …
A. $\frac{31}{18}$
B. $\frac{31}{9}$
C. $\frac{32}{18}$
D. $\frac{33}{9}$
E. $\frac{33}{18}$
Pembahasan:
$\frac{{{A}^{5x}}-{{A}^{-5x}}}{{{A}^{3x}}+{{A}^{-3x}}}$
= $\frac{{{A}^{5x}}-{{A}^{-5x}}}{{{A}^{3x}}+{{A}^{-3x}}}\times \frac{{{A}^{5x}}}{{{A}^{5x}}}$
= $\frac{{{A}^{10x}}-1}{{{A}^{8x}}+{{A}^{2x}}}$
= $\frac{{{\left( {{A}^{2x}} \right)}^{5}}-1}{{{\left( {{A}^{2x}} \right)}^{4}}+{{A}^{2x}}}$
= $\frac{{{2}^{5}}-1}{{{2}^{4}}+2}=\frac{31}{18}$
Jawaban: A
Matematika Dasar SBMPTN 2016 No. 48
Suatu garis yang melalui titik $(0,0)$ membagi persegipanjang dengan titik-titik sudut $(1,0)$, $(5,0)$, $(1,12)$ dan $(5,12)$ menjadi dua bagian yang sama luas. Gradien garis tersebut adalah …
A. $\frac{1}{2}$
B. 1
C. 2
D. $\frac{12}{5}$
E. 3
Pembahasan:
Perhatikan gambar berikut!

Titik E dan F terletak pada garis $y=mx$ yang masing-masing absisnya adalah 1 dan 5, sehingga:
$x=1\to y=mx\Leftrightarrow y=m\Leftrightarrow E(1,m)$
$x=5\to y=mx\Leftrightarrow y=5m\Leftrightarrow E(1,5m)$
Panjang AE = m dan BF = 5m
Luas ABCD = 4 x 12 = 48
Karena garis $y=mx$ membagi dua ABCD menjadi dua bagian yang sama luasnya, maka:
Luas ABFE = $\frac{1}{2}$x Luas ABCD
$\frac{(AE+BF).AB}{2}=\frac{1}{2}\times 48$
$\frac{(m+5m).4}{2}=24$
$24m=48$
$m=2$
Jawaban: C
Matematika Dasar SBMPTN 2016 No. 49
Semua bilangan real $x$ yang memenuhi $\frac{x}{2-x} > \frac{2+x}{x}$ adalah …
A. $-\sqrt{2} < x < 0$ atau $\sqrt{2} < x < 2$
B. $x < -\sqrt{2}$ atau $0 < x < \sqrt{2}$
C. $x < -\sqrt{2}$ atau $x > 2$
D. $x < -\sqrt{2}$ atau $x > \sqrt{2}$
E. $0 < x < 2$
Pembahasan:
$\frac{x}{2-x} > \frac{2+x}{x}$
$\frac{x}{2-x}-\frac{2+x}{x} > 0$
$\frac{{{x}^{2}}}{(2-x)x}-\frac{(2+x)(2-x)}{(2-x)x} > 0$
$\frac{{{x}^{2}}}{(2-x)x}-\frac{4-{{x}^{2}}}{(2-x)x} > 0$
$\frac{2{{x}^{2}}-4}{(2-x)x} > 0$
$\frac{{{x}^{2}}-2}{(2-x)x} > 0$
$\frac{(x-\sqrt{2})(x+\sqrt{2})}{(2-x)x} > 0$
$x=\sqrt{2}$, $x=-\sqrt{2}$, $x\ne 2$, $x\ne 0$
Uji garis bilangan:

HP = {$-\sqrt{2} < x < 0$ atau $\sqrt{2} < x < 2$}
Jawaban: A
Matematika Dasar SBMPTN 2016 No. 50
Jika grafik fungsi $y={{x}^{2}}-(9+a)x+9a$ diperoleh dari grafik fungsi $y={{x}^{2}}-2x-3$ melalui pencerminan terhadap garis $x=4$ maka $a$ = …
A. 7
B. 5
C. 3
D. -5
E. -7
Pembahasan:
$y={{x}^{2}}-2x-3$ dicerminkan terhadap garis $x=4$
$P(x,y)$ dicerminkan terhadap garis $x=4$, menghasilkan bayangan
$P'(x',y')=P'(2.4-x,y)=P'(8-x,y)$
$8-x=x'\Leftrightarrow x=8-x'$ dan $y=y'$ substitusikan ke:
$y={{x}^{2}}-2x-3$
$y'={{(8-x')}^{2}}-2(8-x')-3$
$y=64-16x+{{x}^{2}}-16+2x-3$
$y={{x}^{2}}-14x+45$,
Pada soal bayangan $y={{x}^{2}}-2x-3$ adalah $y={{x}^{2}}-(9+a)x+9a$, maka:
${{x}^{2}}-(9+a)x+9a\equiv {{x}^{2}}-14x+45$
$9a=45\Leftrightarrow a=5$
Jawaban: B
Matematika Dasar SBMPTN 2016 No. 51
Tujuh finalis lomba menyanyi tingkat SMA disuatu kota berasal dari 6 SMA yang berbeda terdiri atas empat pria dan tiga wanita. Diketahui satu pria dan satu wanita berasal dari SMA “A”. Jika urutan tampil diatur bergantian antara pria dan wanita, serta finalis dari SMA “A” tidak tampil berurutan, maka susunan urutan tampil yang mungkin ada sebanyak …
A. 144
B. 108
C. 72
D. 36
E. 35
Pembahasan:
Misalkan: P = Pria, W = Wanita
Susunan yang mungkin agar pria wanita tampil bergantian adalah:
PWPWPWP ada sebanyak 4! x 3! = 144
Misalkan ${{P}_{A}}$ dan ${{W}_{A}}$ menyatakan siswa dari SMA “A” maka susunan siswa SMA “A” tampil berurutan adalah:
${{P}_{A}}{{W}_{A}}PWPWP$ ada sebanyak 3! x 2! = 12
$P{{W}_{A}}{{P}_{A}}WPWP$ ada sebanyak 3! x 2! = 12
$PW{{P}_{A}}{{W}_{A}}PWP$ ada sebanyak 3! x 2! = 12
$PWP{{W}_{A}}{{P}_{A}}WP$ ada sebanyak 3! x 2! = 12
$PWPW{{P}_{A}}{{W}_{A}}P$ ada sebanyak 3! x 2! = 12
$PWPWP{{W}_{A}}{{P}_{A}}$ ada sebanyak 3! x 2! = 12
Seluruhnya ada sebanyak = 6 x 12 = 72
Jadi, susunan urutan tampil diatur bergantian antara pria dan wanita, serta finalis dari SMA “A” tidak tampil berurutan ada sebanyak = 144 – 72 = 72.
Jawaban: C
Matematika Dasar SBMPTN 2016 No. 52
Jika tabel berikut menyatakan hasil fungsi f dan g

Maka $(f\circ g\circ f)(1)+(g\circ f\circ g)(2)$ = …
A. -1
B. 1
C. 2
D. 3
E. 5
Pembahasan:
$(f\circ g\circ f)(1)+(g\circ f\circ g)(2)$
= $f(g(f(1)))+g(f(g(2)))$
= $f(g(3))+g(f(1))$
= $f(2)+g(3)$
= $1+2=3$
Jawaban: D
Matematika Dasar SBMPTN 2016 No. 53
Jika fungsi $f$ dan $g$ mempunyai invers dan memenuhi $f(2x)=g(x+3)$, maka ${{f}^{-1}}(x)$ = …
A. ${{g}^{-1}}\left( \frac{x}{2}-\frac{3}{2} \right)$
B. ${{g}^{-1}}(2x-6)$
C. $2{{g}^{-1}}(x)-3$
D. $2{{g}^{-1}}(x)-6$
E. $2{{g}^{-1}}(x)+6$
Pembahasan:
$f(2x)=g(x+3)$
${{f}^{-1}}(g(x+3))=2x$
$({{f}^{-1}}\circ g)(x+3)=2x$
$({{f}^{-1}}\circ g)(x)=2(x-3)$
$({{f}^{-1}}\circ g)(x)=2x-6$
${{f}^{-1}}(g(x))=2x-6$
${{f}^{-1}}(x)=2{{g}^{-1}}(x)-6$
Jawaban: D
Matematika Dasar SBMPTN 2016 No. 54
Diketahui matriks $A=\left( \begin{matrix} 8 & a \\ a & 1 \\ \end{matrix} \right)$, $B=\left( \begin{matrix} 1 & -1 \\ b & 1 \\ \end{matrix} \right)$, dan C adalah matriks berukuran 2x2 yang mempunyai invers. Jika AC dan BC tidak memiliki invers, maka $3{{a}^{2}}+4{{b}^{3}}$ = …
A. 16
B. 20
C. 24
D. 28
E. 36
Pembahasan:
AC tidak memiliki invers, maka det(AC) = 0
$|AC|=0$
$|A||C|=0$, karena C mempunyai invers, maka:
det(A) = 0
$8-{{a}^{2}}=0\Leftrightarrow {{a}^{2}}=8$
BC tidak memiliki invers, maka det(BC) = 0
$|BC|=0$
$|B||C|=0$, karena C mempunyai invers, maka:
det(B) = 0
$\left| \begin{matrix} 1 & -1 \\ b & 1 \\ \end{matrix} \right|=0\Leftrightarrow 1+b=0\Leftrightarrow b=-1$
$3{{a}^{2}}+4{{b}^{3}}=3.8+{{4.1}^{3}}=28$
Jawaban: D
Matematika Dasar SBMPTN 2016 No. 55
Misalkan ${{U}_{k}}$ dan ${{S}_{k}}$ berturut-turut menyatakan suku ke-k dan jumlah k suku pertama suatu barisan aritmetika. Jika ${{U}_{2}}-{{U}_{4}}$ + ${{U}_{6}}-{{U}_{8}}$ + ${{U}_{10}}-{{U}_{12}}$ + ${{U}_{14}}-{{U}_{16}}$ + ${{U}_{18}}=20$, maka ${{S}_{19}}$ = …
A. 630
B. 380
C. 210
D. 105
E. 21
Pembahasan:
${{U}_{2}}-{{U}_{4}}$ + ${{U}_{6}}-{{U}_{8}}$ + ${{U}_{10}}-{{U}_{12}}$ + ${{U}_{14}}-{{U}_{16}}$ + ${{U}_{18}}=20$
$(a+b)-(a+3b)$ + $(a+5b)-(a+7b)$ + $(a+9b)-(a+11b)$ + $(a+13b)-(a+15b)$ + $(a+17b)=20$
$a+9b=20$
${{S}_{19}}=\frac{19}{2}(2a+18b)$
${{S}_{19}}=19(a+9b)$
${{S}_{19}}=19.20=380$
Jawaban: B
Matematika Dasar SBMPTN 2016 No. 56

Diketahui semua titik sudut segienam beraturan ABCDEF terletak pada lingkaran yang berjari-jari 2 cm seperti pada gambar. Luas daerah yang tidak diarsir pada segienam tersebut adalah … cm$^2$.
A. 3
B. $2\sqrt{3}$
C. 4
D. $3\sqrt{3}$
E. $6\sqrt{3}$
Pembahasan:
Perhatikan gambar berikut!

Karena ABCDEF adalah segienam berarutan, maka dengan jari-jari 2 cm, maka OA = OB = OC = OD = OE = OF = AB = BC = CD = DE = EF = AF, sehingga:
Segitiga ABO adalah segitiga sama sisi dengan panjang sisi 2 cm.
Pada segitiga AQO berlaku pythagoras, yaitu:
$A{{Q}^{2}}=O{{A}^{2}}-O{{Q}^{2}}$
${{t}^{2}}={{2}^{2}}-{{1}^{2}}$
$t=\sqrt{3}$
Luas ABO + Luas OEF adalah
= $\frac{1}{2}.AP.t+\frac{1}{2}.PF.t$
= $\frac{1}{2}t(AP+PF)$
= $\frac{1}{2}\sqrt{3}.2$
= $\sqrt{3}$
Luas PCD adalah:
= $\frac{1}{2}.CD.2t$
= $\frac{1}{2}.2.2\sqrt{3}$
= $2\sqrt{3}$
Luas arsiran adalah:
= Luas ABO + Luas OEF + Luas PCD
= $\sqrt{3}+2\sqrt{3}=3\sqrt{3}$
Jawaban: D
Matematika Dasar SBMPTN 2016 No. 57
Nilai ujian matematika 30 siswa pada suatu kelas berupa bilangan cacah tidak lebih daripada 10. Rata-rata nilai mereka adalah 8 dan hanya terdapat 5 siswa yang memperoleh nilai 7. Jika $p$ menyatakan banyak siswa yang memperoleh nilai kurang dari 7, maka nilai $p$ terbesar yang mungkin adalah …
A. 5
B. 7
C. 9
D. 11
E. 14
Pembahasan:
$\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+...+{{x}_{30}}}{30}=8$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+...+{{x}_{30}}=240$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+...+{{x}_{25}}+5.7=240$
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+...+{{x}_{25}}=205$
Agar $p$ maksimal maka siswa bernilai 6 $p$ dan sisanya bernilai maksimal yaitu sebanyak $(25-p)$ bernilai 10, sehingga:
$6p+(25-p).10\le 205$
$-4p+250\le 205$
$-4p\le -45\Leftrightarrow p\le 11,25$
Karena $p$ bilangan asli maka $p$ terbesar adalah 11.
Jawaban: D
Matematika Dasar SBMPTN 2016 No. 58
Jika $a$ dan $b$ bilangan bulat, serta $\underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}-x-b}{2-x}=a$, maka $b-a$ = …
A. -5
B. -3
C. -1
D. 2
E. 5
Pembahasan:
$\underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}-x-b}{2-x}=a$
Jika $x=2$, maka:
${{x}^{2}}-x-b=0$
${{2}^{2}}-2-b=0\Leftrightarrow b=2$
$\underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}-x-2}{2-x}=a$
$\underset{x\to 2}{\mathop{\lim }}\,\frac{(x-2)(x+1)}{-(x-2)}=a$
$\underset{x\to 2}{\mathop{\lim }}\,-(x+1)=a$
$-(2+1)=a\Leftrightarrow a=-3$
maka nilai $b-a=2-(-3)=5$
Jawaban: E
Matematika Dasar SBMPTN 2016 No. 59
Jika $(x,y)=(1,3)$ dan $(x,y)=(a,1)$ merupakan penyelesaian $x-2y=b$ dan $cx+dy=10$, maka $a+b+c+d$ = …
A. -9
B. -6
C. 0
D. 3
E. 9
Pembahasan:
$x-2y=b$
$cx+dy=10$
Disusun dalam bentuk matriks menjadi:
$\left( \begin{matrix} 1 & -2 \\ c & d \\ \end{matrix} \right)\left( \begin{matrix} x \\ y \\ \end{matrix} \right)=\left( \begin{matrix} b \\ 10 \\ \end{matrix} \right)$
Karena $(x,y)=(1,3)$ dan $(x,y)=(a,1)$, maka:
$\left( \begin{matrix} 1 & -2 \\ c & d \\ \end{matrix} \right)\left( \begin{matrix} 1 & a \\ 3 & 1 \\ \end{matrix} \right)=\left( \begin{matrix} b & b \\ 10 & 10 \\ \end{matrix} \right)$
$\left( \begin{matrix} -5 & a-2 \\ c+3d & ac+d \\ \end{matrix} \right)=\left( \begin{matrix} b & b \\ 10 & 10 \\ \end{matrix} \right)$
$b=-5$
$a-2=b$
$a-2=-5\Leftrightarrow a=-3$
$c+3d=10\Leftrightarrow c=10-3d$
$ac+d=10$
$-3(10-3d)+d=10$
$-30+9d+d=10$
$10d=40\Leftrightarrow d=4$
$c=10-3d\Leftrightarrow c=10-3.4=-2$
$a+b+c+d=-3+(-5)+(-2)+4=-6$
Jawaban: B
Matematika Dasar SBMPTN 2016 No. 60
Semua bilangan real $x$ yang memenuhi $|x-2| > {{x}^{2}}-4$ adalah …
A. $x < -2$ atau $x > 3$
B. $x < -2$ atau $x > 2$
C. $x < -2$ atau $x > 0$
D. $-2 < x < 3$
E. $-3 < x < 2$
Pembahasan:
Sesuai definisi nilai mutlak:
$|x-2|=x-2$ jika $x-2\ge 0 \Leftrightarrow x\ge 2$
$|x-2|=-x+2$ jika $x-2 < 0 \Leftrightarrow x < 2$
a) Untuk $x\ge 2$ maka:
$|x-2| > {{x}^{2}}-4$
$x-2 > {{x}^{2}}-4$
$-{{x}^{2}}+x+2 > 0$
${{x}^{2}}-x-2 < 0$
$(x-2)(x+1) < 0$
$-1 < x < 2$ (tidak memenuhui syarat $x\ge 2$)
b) Untuk $x < 2$ maka:
$|x-2| > {{x}^{2}}-4$
$-x+2 > {{x}^{2}}-4$
$-{{x}^{2}}-x+6 > 0$
${{x}^{2}}+x-6 > 0$
$(x+3)(x-2) < 0$
$-3 < x < 2$ (memenuhui syarat)
HP: {$-3 < x < 2$}
Jawaban: E
Artikel Terkait:
|

Post a Comment for "Pembahasan SBMTPN 2016 TKPA (Matematika Dasar) "
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.