Pembahasan Soal SBMPTN 2016 Matematika IPA
Hai.... semua....! Ada postingan baru lagi nih, kali ini Soal dan Pembahasan Matematika IPA SBMPTN 2016 Kode 217. Seperti biasa, saya selalu menyediakan link download soal agar bisa dikerjakan/dijawab secara mandiri dan offline. Sementara untuk pembahasannya silahkan dilihat di postingannya ini.
Matematika IPA SBMPTN 2016 No. 1
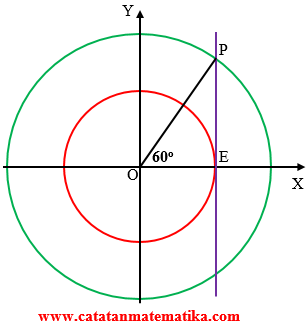
Diketahui dua lingkaran berpusat di titik O(0,0) berjari-jari $r$ dan $R$ dengan $r < R$. Sebuah garis $l$ menyinggung lingkaran dalam di titik E dan memotong lingkaran luar di titik P. Jika diketahui selisih antara luas lingkaran luar dan lingkaran dalam $36\pi $ dan $\angle EOP={{60}^{o}}$, maka persamaan lingkaran luar adalah …
A. ${{x}^{2}}+{{y}^{2}}=36$
B. ${{x}^{2}}+{{y}^{2}}=40$
C. ${{x}^{2}}+{{y}^{2}}=44$
D. ${{x}^{2}}+{{y}^{2}}=48$
E. ${{x}^{2}}+{{y}^{2}}=52$
Pembahasan:
Matematika IPA SBMPTN 2016 No. 1
Diketahui dua lingkaran berpusat di titik O(0,0) berjari-jari $r$ dan $R$ dengan $r < R$. Sebuah garis $l$ menyinggung lingkaran dalam di titik E dan memotong lingkaran luar di titik P. Jika diketahui selisih antara luas lingkaran luar dan lingkaran dalam $36\pi $ dan $\angle EOP={{60}^{o}}$, maka persamaan lingkaran luar adalah …
A. ${{x}^{2}}+{{y}^{2}}=36$
B. ${{x}^{2}}+{{y}^{2}}=40$
C. ${{x}^{2}}+{{y}^{2}}=44$
D. ${{x}^{2}}+{{y}^{2}}=48$
E. ${{x}^{2}}+{{y}^{2}}=52$
Pembahasan:

Luas lingkaran luar – luas lingkaran dalam = $36\pi $$\cos {{60}^{o}}=\frac{OE}{OP}$
$\frac{1}{2}=\frac{r}{R}\Leftrightarrow r=\frac{1}{2}R$
$\pi {{R}^{2}}-\pi {{r}^{2}}=36\pi $
${{R}^{2}}-{{r}^{2}}=36$
${{R}^{2}}-{{\left( \frac{1}{2}R \right)}^{2}}=36$
${{R}^{2}}-\frac{1}{4}{{R}^{2}}=36$
$\frac{3}{4}{{R}^{2}}=36$
${{R}^{2}}=48$
Persamaan lingkaran luar:
${{x}^{2}}+{{y}^{2}}={{R}^{2}}\Leftrightarrow {{x}^{2}}+{{y}^{2}}=48$
Jawaban: D
Matematika IPA SBMPTN 2016 No. 2
Misalkan segitiga ABC adalah segitiga siku-siku pada titik C. Jika panjang sisi di hadapan titik A, B, C berturut-turut adalah a, b, c maka cos 2A = …
A. $\frac{{{b}^{2}}-{{a}^{2}}}{{{c}^{2}}}$
B. $\frac{{{a}^{2}}-{{b}^{2}}}{{{c}^{2}}}$
C. $\frac{{{b}^{2}}-{{c}^{2}}}{{{a}^{2}}}$
D. $\frac{{{c}^{2}}-{{a}^{2}}}{{{b}^{2}}}$
E. $\frac{{{a}^{2}}-{{b}^{2}}}{{{b}^{2}}}$
Pembahasan:

${{b}^{2}}={{c}^{2}}-{{a}^{2}}$
$\cos A=\frac{b}{c}$
$\cos 2A=2{{\cos }^{2}}A-1$
$\cos 2A=2{{\left( \frac{b}{c} \right)}^{2}}-1$
$\cos 2A=\frac{2{{b}^{2}}-{{c}^{2}}}{{{c}^{2}}}$
$\cos 2A=\frac{{{b}^{2}}+{{b}^{2}}-{{c}^{2}}}{{{c}^{2}}}$
$\cos 2A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}-{{c}^{2}}}{{{c}^{2}}}$
$\cos 2A=\frac{{{b}^{2}}-{{a}^{2}}}{{{c}^{2}}}$
Jawaban: A
Matematika IPA SBMPTN 2016 No. 3
Fungsi $f(x)={{\sec }^{2}}x-\tan x\sec x$ untuk $0 < x < 2\pi $, $x\ne \frac{\pi }{2}$ dan $x\ne \frac{3\pi }{2}$ naik pada interval …
A. $0 < x < {{90}^{o}}$ atau ${{90}^{o}} < x < {{180}^{o}}$
B. $0 < x <{{90}^{o}}$ atau ${{270}^{o}} < x < {{360}^{o}}$
C. ${{90}^{o}} < x < {{180}^{o}}$
D. ${{90}^{o}} < x < {{270}^{o}}$
E. ${{90}^{o}} < x < {{200}^{o}}$
Pembahasan:
$f(x)={{\sec }^{2}}x-\tan x\sec x$
$f'(x)=2\sec x.\sec x\tan x-({{\sec }^{2}}x.\sec x+\tan x.\sec x\tan x)$
$f'(x)=-\sec x(-2\sec x\tan x+{{\sec }^{2}}x+{{\tan }^{2}}x)$
$f'(x)=-\sec x{{(\sec x-\tan x)}^{2}}$
$f(x)$ naik maka $f'(x) > 0$
$-\sec x{{(\sec x-\tan x)}^{2}} > 0$
$-\sec x > 0$
$\sec x < 0$
$\frac{1}{\cos x} < 0$
$\cos x < 0$
${{90}^{o}} < x < {{270}^{o}}$
Jawaban: D
Matematika IPA SBMPTN 2016 No. 4
Jika titik (a,b) dicerminkan terhadap garis y = x – 1 menjadi titik (c,d), maka 2c + d = …
A. 2a + b – 1
B. 2a – b – 1
C. a – 2b – 1
D. 2a + b + 1
E. a + 2b + 1
Pembahasan:
Pencerminan titik (x,y) terhadap garis y = x – k
$\left( \begin{matrix} x' \\ y' \\ \end{matrix} \right)=\left( \begin{matrix} y+k \\ x-k \\ \end{matrix} \right)$
Dari soal (a,b) = (x,y) dan (c,d) = (x’,y’) maka:
$\left( \begin{matrix} c \\ d \\ \end{matrix} \right)=\left( \begin{matrix} b+1 \\ a-1 \\ \end{matrix} \right)$
c = b + 1 dan d = a – 1
2c + d = 2(b + 1) + a – 1 = a + 2b + 1
Jawaban: E
Matematika IPA SBMPTN 2016 No. 5
Diketahui kubus ABCD.EFGH. Titik M berada di rusuk AD sedemikian sehingga AM : MD = 1 : 2. Titik N berada di rusuk CD sedemikian sehingga CN : ND = 1 : 2. Titik P berada di rusuk DH sedemikian sehingga DP : PH = 2 : 1. Jika $\alpha $ adalah sudut antara bidang MNP dan bidang ACGE, maka nilai sin $\alpha $ = …
A. $\frac{1}{3}\sqrt{6}$
B. $\frac{1}{3}\sqrt{5}$
C. $\frac{1}{3}\sqrt{4}$
D. $\frac{1}{3}\sqrt{3}$
E. $\frac{1}{3}\sqrt{2}$
Pembahasan:
Untuk mempermudah perhitungan, kita misalkan panjang rusuk kubus ABCD.EFGH adalah 3 satuan.

$\frac{1}{2}=\frac{r}{R}\Leftrightarrow r=\frac{1}{2}R$
$\pi {{R}^{2}}-\pi {{r}^{2}}=36\pi $
${{R}^{2}}-{{r}^{2}}=36$
${{R}^{2}}-{{\left( \frac{1}{2}R \right)}^{2}}=36$
${{R}^{2}}-\frac{1}{4}{{R}^{2}}=36$
$\frac{3}{4}{{R}^{2}}=36$
${{R}^{2}}=48$
Persamaan lingkaran luar:
${{x}^{2}}+{{y}^{2}}={{R}^{2}}\Leftrightarrow {{x}^{2}}+{{y}^{2}}=48$
Jawaban: D
Matematika IPA SBMPTN 2016 No. 2
Misalkan segitiga ABC adalah segitiga siku-siku pada titik C. Jika panjang sisi di hadapan titik A, B, C berturut-turut adalah a, b, c maka cos 2A = …
A. $\frac{{{b}^{2}}-{{a}^{2}}}{{{c}^{2}}}$
B. $\frac{{{a}^{2}}-{{b}^{2}}}{{{c}^{2}}}$
C. $\frac{{{b}^{2}}-{{c}^{2}}}{{{a}^{2}}}$
D. $\frac{{{c}^{2}}-{{a}^{2}}}{{{b}^{2}}}$
E. $\frac{{{a}^{2}}-{{b}^{2}}}{{{b}^{2}}}$
Pembahasan:

${{b}^{2}}={{c}^{2}}-{{a}^{2}}$
$\cos A=\frac{b}{c}$
$\cos 2A=2{{\cos }^{2}}A-1$
$\cos 2A=2{{\left( \frac{b}{c} \right)}^{2}}-1$
$\cos 2A=\frac{2{{b}^{2}}-{{c}^{2}}}{{{c}^{2}}}$
$\cos 2A=\frac{{{b}^{2}}+{{b}^{2}}-{{c}^{2}}}{{{c}^{2}}}$
$\cos 2A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}-{{c}^{2}}}{{{c}^{2}}}$
$\cos 2A=\frac{{{b}^{2}}-{{a}^{2}}}{{{c}^{2}}}$
Jawaban: A
Matematika IPA SBMPTN 2016 No. 3
Fungsi $f(x)={{\sec }^{2}}x-\tan x\sec x$ untuk $0 < x < 2\pi $, $x\ne \frac{\pi }{2}$ dan $x\ne \frac{3\pi }{2}$ naik pada interval …
A. $0 < x < {{90}^{o}}$ atau ${{90}^{o}} < x < {{180}^{o}}$
B. $0 < x <{{90}^{o}}$ atau ${{270}^{o}} < x < {{360}^{o}}$
C. ${{90}^{o}} < x < {{180}^{o}}$
D. ${{90}^{o}} < x < {{270}^{o}}$
E. ${{90}^{o}} < x < {{200}^{o}}$
Pembahasan:
$f(x)={{\sec }^{2}}x-\tan x\sec x$
$f'(x)=2\sec x.\sec x\tan x-({{\sec }^{2}}x.\sec x+\tan x.\sec x\tan x)$
$f'(x)=-\sec x(-2\sec x\tan x+{{\sec }^{2}}x+{{\tan }^{2}}x)$
$f'(x)=-\sec x{{(\sec x-\tan x)}^{2}}$
$f(x)$ naik maka $f'(x) > 0$
$-\sec x{{(\sec x-\tan x)}^{2}} > 0$
$-\sec x > 0$
$\sec x < 0$
$\frac{1}{\cos x} < 0$
$\cos x < 0$
${{90}^{o}} < x < {{270}^{o}}$
Jawaban: D
Matematika IPA SBMPTN 2016 No. 4
Jika titik (a,b) dicerminkan terhadap garis y = x – 1 menjadi titik (c,d), maka 2c + d = …
A. 2a + b – 1
B. 2a – b – 1
C. a – 2b – 1
D. 2a + b + 1
E. a + 2b + 1
Pembahasan:
Pencerminan titik (x,y) terhadap garis y = x – k
$\left( \begin{matrix} x' \\ y' \\ \end{matrix} \right)=\left( \begin{matrix} y+k \\ x-k \\ \end{matrix} \right)$
Dari soal (a,b) = (x,y) dan (c,d) = (x’,y’) maka:
$\left( \begin{matrix} c \\ d \\ \end{matrix} \right)=\left( \begin{matrix} b+1 \\ a-1 \\ \end{matrix} \right)$
c = b + 1 dan d = a – 1
2c + d = 2(b + 1) + a – 1 = a + 2b + 1
Jawaban: E
Matematika IPA SBMPTN 2016 No. 5
Diketahui kubus ABCD.EFGH. Titik M berada di rusuk AD sedemikian sehingga AM : MD = 1 : 2. Titik N berada di rusuk CD sedemikian sehingga CN : ND = 1 : 2. Titik P berada di rusuk DH sedemikian sehingga DP : PH = 2 : 1. Jika $\alpha $ adalah sudut antara bidang MNP dan bidang ACGE, maka nilai sin $\alpha $ = …
A. $\frac{1}{3}\sqrt{6}$
B. $\frac{1}{3}\sqrt{5}$
C. $\frac{1}{3}\sqrt{4}$
D. $\frac{1}{3}\sqrt{3}$
E. $\frac{1}{3}\sqrt{2}$
Pembahasan:
Untuk mempermudah perhitungan, kita misalkan panjang rusuk kubus ABCD.EFGH adalah 3 satuan.

Dari gambar,
$\alpha =\angle (MNP,ACGE)$
$\alpha =\angle (MNP,MNN'M')$
$\alpha =\angle (MNP,QQ')$
$\alpha =\angle (PQ,QR)$
Perhatikan segitiga PQR siku-siku di R dengan:
$PR=\sqrt{2}$, QR = 2
$PQ=\sqrt{P{{R}^{2}}+Q{{R}^{2}}}$
$PQ=\sqrt{{{(\sqrt{2})}^{2}}+{{2}^{2}}}$
$PQ=\sqrt{6}$
$\sin \alpha =\frac{PR}{PQ}$
$\sin \alpha =\frac{\sqrt{2}}{\sqrt{6}}$
$\sin \alpha =\frac{1}{\sqrt{3}}=\frac{1}{3}\sqrt{3}$
Jawaban: D
Matematika IPA SBMPTN 2016 No. 6
Diketahui sisa pembagian suku banyak $f(x)-g(x)$ oleh ${{x}^{2}}+x-2$ adalah $x$, sisa pembagian $f(x)+g(x)$ oleh ${{x}^{2}}-3x+2$ adalah $x+1$, maka sisa pembagian ${{(f(x))}^{2}}+{{(g(x))}^{2}}$ oleh $x-1$ adalah …
A. $\frac{5}{2}$
B. $\frac{5}{4}$
C. $\frac{1}{4}$
D. 1
E. 4
Pembahasan:
Yang dibagi = pembagi x hasil + sisa
$f(x)-g(x)$ = (${{x}^{2}}+x-2$).hasil + $x$
$f(x)-g(x)$ = $(x+2)(x-1)$.hasil + $x$
Untuk x = 1, maka:
$f(1)-g(1)$ = 1 …. pers (1)
$f(x)+g(x)$ = $({{x}^{2}}-3x+2)$.hasil + $x+1$
$f(x)+g(x)$ = $(x-1)(x-2)$.hasil + $x+1$
Untuk x = 1, maka:
$f(1)+g(1)$ = 2 …. pers (2)
$f(1)-g(1)$ = 1 …. pers (1)
--------------------------------- (+)
$2f(1)=3\Leftrightarrow f(1)=\frac{3}{2}$
$f(1)+g(1)$ = 2
$f(1)-g(1)$ = 1
------------------- (-)
$2g(1)=1\Leftrightarrow g(1)=\frac{1}{2}$
Dengan Teorema Sisa:
Sisa pembagian ${{(f(x))}^{2}}+{{(g(x))}^{2}}$ oleh $x-1$ adalah:
= ${{(f(1))}^{2}}+{{(g(1))}^{2}}$
= ${{\left( \frac{3}{2} \right)}^{2}}+{{\left( \frac{1}{2} \right)}^{2}}$
= $\frac{10}{4}=\frac{5}{2}$
Jawaban: A
Matematika IPA SBMPTN 2016 No. 7
Grafik $y={{3}^{x+1}}-{{\left( \frac{1}{9} \right)}^{x}}$ berada di bawah grafik $y={{3}^{x}}+1$ jika …
A. 0 < x < 1
B. x > 1
C. x < 0
D. x > 3
E. 1 < x < 3
Pembahasan:
${{y}_{1}}={{3}^{x+1}}-{{\left( \frac{1}{9} \right)}^{x}}$ di bawah ${{y}_{2}}={{3}^{x}}+1$ maka:
${{y}_{1}} < {{y}_{2}}$
${{3}^{x+1}}-{{\left( \frac{1}{9} \right)}^{x}} < {{3}^{x}}+1$
${{3.3}^{x}}-\frac{1}{{{({{3}^{x}})}^{2}}} < {{3}^{x}}+1$
${{2.3}^{x}}-\frac{1}{{{({{3}^{x}})}^{2}}}-1 < 0$
$2{{({{3}^{x}})}^{3}}-1-{{({{3}^{x}})}^{2}} < 0$
$2{{({{3}^{x}})}^{3}}-{{({{3}^{x}})}^{2}}-1 < 0$
Misal: $y={{3}^{x}}$ maka:
$2{{y}^{3}}-{{y}^{2}}-1 < 0$
$(y-1)(2{{y}^{2}}+y+1) < 0$; $2{{y}^{2}}+y+1 > 0$ (DEFINIT POSITIF) maka:
$y-1 < 0$
$y < 1$
${{3}^{x}} < {{3}^{0}}\Leftrightarrow x < 0$
Jawaban: C
Matematika IPA SBMPTN 2016 No. 8
Nilai dari $\underset{x\to 2}{\mathop{\lim }}\,\frac{\sqrt{1-\cos (x-2)}}{\sqrt{{{x}^{2}}-2x}}$
A. 0
B. $\frac{1}{2}$
C. $\frac{3}{4}$
D. 1
E. $\infty $
Pembahasan:
$\underset{x\to 2}{\mathop{\lim }}\,\frac{\sqrt{1-\cos (x-2)}}{\sqrt{{{x}^{2}}-2x}}$
$=\sqrt{\underset{x\to 2}{\mathop{\lim }}\,\frac{1-\cos (x-2)}{{{x}^{2}}-2x}}$
$=\sqrt{\underset{x\to 2}{\mathop{\lim }}\,\frac{2{{\sin }^{2}}\frac{1}{2}(x-2)}{{{x}^{2}}-2x}}$
$=\sqrt{\underset{x\to 2}{\mathop{\lim }}\,2.\frac{\sin \frac{1}{2}(x-2)}{x}.\frac{\sin \frac{1}{2}(x-2)}{(x-2)}}$
$=\sqrt{2.\frac{\sin \frac{1}{2}(2-2)}{2}.\frac{1}{2}}$
$=\sqrt{2.\frac{0}{2}.\frac{1}{2}}$
= 0
Jawaban: A
Matematika IPA SBMPTN 2016 No. 9
Suatu barisan geometri semua sukunya positif. Jika $\frac{{{u}_{1}}+{{u}_{2}}}{{{u}_{3}}+{{u}_{4}}}=\frac{1}{9}$ maka $\frac{{{u}_{1}}+{{u}_{2}}+{{u}_{3}}+{{u}_{4}}}{{{u}_{2}}+{{u}_{3}}}$ = …
A. $\frac{10}{9}$
B. 3
C. $\frac{10}{3}$
D. 4
E. 10
Pembahasan:
Barisan Geometri: ${{u}_{n}}=a{{r}^{n-1}}$
$\frac{{{u}_{1}}+{{u}_{2}}}{{{u}_{3}}+{{u}_{4}}}=\frac{1}{9}$
$\frac{a+ar}{a{{r}^{2}}+a{{r}^{3}}}=\frac{1}{9}$
$\frac{a(1+r)}{a{{r}^{2}}(1+r)}=\frac{1}{9}$
$\frac{1}{{{r}^{2}}}=\frac{1}{9}$
${{r}^{2}}=9\Leftrightarrow r=3$
$\frac{{{u}_{1}}+{{u}_{2}}+{{u}_{3}}+{{u}_{4}}}{{{u}_{2}}+{{u}_{3}}}=\frac{a+ar+a{{r}^{2}}+a{{r}^{3}}}{ar+a{{r}^{2}}}$
$=\frac{a(1+r+{{r}^{2}}+{{r}^{3}})}{a(r+{{r}^{2}})}$
$=\frac{1+r+{{r}^{2}}+{{r}^{3}}}{r+{{r}^{2}}}$
$=\frac{1+3+{{3}^{2}}+{{3}^{3}}}{3+{{3}^{2}}}$
$=\frac{40}{12}=\frac{10}{3}$
Jawaban: C
Matematika IPA SBMPTN 2016 No. 10
Misalkan $f(x)=a\sqrt{x}+\frac{b}{\sqrt{x}}$ mempunyai titik belok di (4,13). Nilai a + b = …
A. $\frac{91}{8}$
B. $\frac{81}{8}$
C. $\frac{71}{8}$
D. $\frac{61}{8}$
E. $\frac{51}{8}$
Pembahasan:
Titik $(4,13)$ pada $f(x)=a\sqrt{x}+\frac{b}{\sqrt{x}}$ maka:
$13=a\sqrt{4}+\frac{b}{\sqrt{4}}$
$13=2a+\frac{b}{2}$
$4a+b=26$
Titik $(4,13)$ adalah titik belok maka $f''(4)=0$
$f(x)=a\sqrt{x}+\frac{b}{\sqrt{x}}$
$f(x)=a{{x}^{\frac{1}{2}}}+b{{x}^{-\frac{1}{2}}}$
$f'(x)=\frac{1}{2}a{{x}^{-\frac{1}{2}}}-\frac{1}{2}b{{x}^{-\frac{3}{2}}}$
$f''(x)=-\frac{1}{4}a{{x}^{-\frac{3}{2}}}+\frac{3}{4}b{{x}^{-\frac{5}{2}}}$
$f''(x)=\frac{-a}{4\sqrt{{{x}^{3}}}}+\frac{3b}{4\sqrt{{{x}^{5}}}}$
$f''(4)=\frac{-a}{4\sqrt{{{4}^{3}}}}+\frac{3b}{4\sqrt{{{4}^{5}}}}=0$
$\frac{-a}{32}+\frac{3b}{128}=0$
$-4a+3b=0$
$4a+b=26$
--------------- (+)
$4b=26\Leftrightarrow b=\frac{13}{2}$
$4a+b=26$
$4a+\frac{13}{2}=26$
$8a+13=52\Leftrightarrow a=\frac{39}{8}$
$a+b=\frac{39}{8}+\frac{13}{2}=\frac{91}{8}$
Jawaban: A
Matematika IPA SBMPTN 2016 No. 11
Diketahui fungsi $f(x)=f(x+2)$ untuk setiap $x$. Jika $\int\limits_{0}^{2}{f(x)dx}=B$, maka $\int\limits_{3}^{7}{f(x+8)dx}$ = …
A. B
B. 2B
C. 3B
D. 4B
E. 5B
Pembahasan:
Misalkan $\int\limits_{0}^{1}{f(x)dx}=A$
$\int\limits_{0}^{2}{f(x)dx}=B$, dengan sifat-sifat integral tertentu, maka:
$\int\limits_{0}^{1}{f(x)dx}+\int\limits_{1}^{2}{f(x)dx}=B$
$A+\int\limits_{1}^{2}{f(x)dx}=B$
$\int\limits_{1}^{2}{f(x)dx}=B-A$
$\int\limits_{3}^{7}{f(x+8)dx}$
$=\int\limits_{3}^{7}{f(x)dx}$
$=\int\limits_{3}^{4}{f(x)dx}+\int\limits_{4}^{6}{f(x)dx}+\int\limits_{6}^{7}{f(x)dx}$
Misalkan, ${{I}_{1}}=\int\limits_{3}^{4}{f(x)dx}$ substitusi $x=u+2$
${{I}_{1}}=\int\limits_{1}^{2}{f(u+2)du}$
${{I}_{1}}=\int\limits_{1}^{2}{f(u)du}=B-A$
Misalkan, ${{I}_{2}}=\int\limits_{4}^{6}{f(x)dx}$ substitusi $x=u+4$
${{I}_{2}}=\int\limits_{0}^{2}{f(u+4)du}$
${{I}_{1}}=\int\limits_{0}^{2}{f(u)du}=B$
Misalkan, ${{I}_{3}}=\int\limits_{6}^{7}{f(x)dx}$ substitusi $x=u+6$
${{I}_{3}}=\int\limits_{0}^{1}{f(u+6)du}$
${{I}_{1}}=\int\limits_{0}^{1}{f(u)du}=A$
Jadi,
$\int\limits_{3}^{7}{f(x+8)dx}={{I}_{1}}+{{I}_{2}}+{{I}_{3}}$ = B – A + B + A = 2B.
Jawaban: B
Matematika IPA SBMPTN 2016 No. 12
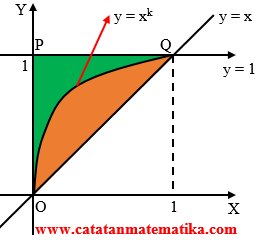
Diketahui fungsi $f(x)={{x}^{k}}$ dan $g(x)=x$. Misalkan D adalah daerah yang dibatasi oleh kurva $g$, sumbu Y dan y = 1. Jika kurva $f$ membagi daerah D sama besar, maka k = …
A. $\frac{1}{3}$
B. $\frac{2}{3}$
C. 1
D. 2
E. 3
Pembahasan:

Luas D = Luas segitiga OPQ = $\frac{1}{2}.1.1=\frac{1}{2}$
Karena kurva $y={{x}^{k}}$ membagi daerah D sama besar, maka:
Luas daerah Hijau = 1/2 x Luas D
$\int\limits_{0}^{1}{(1-{{x}^{k}})dx}=\frac{1}{2}.\frac{1}{2}$
$\left. \left( x-\frac{1}{k+1}{{x}^{k+1}} \right) \right|_{0}^{1}=\frac{1}{4}$
$\left( 1-\frac{1}{k+1}{{.1}^{k+1}} \right)-\left( 0-\frac{1}{k+1}{{.0}^{k+1}} \right)=\frac{1}{4}$
$1-\frac{1}{k+1}=\frac{1}{4}$
$1-\frac{1}{4}=\frac{1}{k+1}$
$\frac{3}{4}=\frac{1}{k+1}$
$3k+3=4\Leftrightarrow 3k=1\Leftrightarrow k=\frac{1}{3}$
Jawaban: A
Matematika IPA SBMPTN 2016 No. 13
Banyaknya bilangan genap n = abc dengan 3 digit sehingga 3 < b < c adalah …
A. 48
B. 54
C. 60
D. 64
E. 72
Pembahasan:
N = abc genap jika c bilangan genap, nilai c yang memenuhi adalah 6 dan 8. Pilihan nilai a = {1, 2, 3, 4, 5, 6, 7, 8, 9} ada sembilan pilihan.
Jika c = 6, maka b = {5, 4} dan a = {1, 2, 3, 4, 5, 6, 7, 8, 9} maka banyak bilangan: 2 x 9 = 18 bilangan.
Jika c = 8, maka b = {7, 6, 5, 4} dan a = {1, 2, 3, 4, 5, 6, 7, 8, 9} maka banyak bilangan: 4 x 9 = 36 bilangan.
Jumlah seluruh bilangan = 18 + 36 = 54 bilangan.
Jawaban: B
Matematika IPA SBMPTN 2016 No. 14
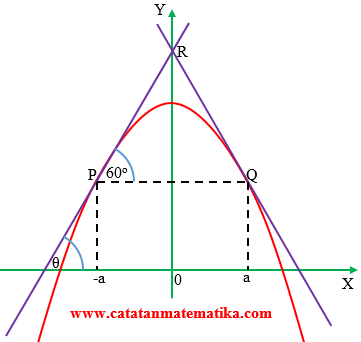
Garis singgung kurva $y=3-{{x}^{2}}$ di titik P(-a,b) dan Q(a,b) memotong sumbu Y di titik R. Nilai a yang membuat segitiga PQR sama sisi adalah …
A. $2\sqrt{3}$
B. $\sqrt{3}$
C. $\frac{1}{2}\sqrt{3}$
D. $\frac{1}{3}\sqrt{3}$
E. $\frac{1}{4}\sqrt{3}$
Pembahasan:

Segitiga PQR sama sisi, maka masing-masing sudutnya ${{60}^{o}}$, maka $\theta ={{60}^{o}}$, kita peroleh gradien garis singgung yang melalui titik P(-a,b) adalah $\tan {{60}^{o}}=\sqrt{3}$.
$y=3-{{x}^{2}}$
$\frac{dy}{dx}=-2x$ melalui titik P(-a,b)
${{\left. \frac{dy}{dx} \right|}_{x=-a}}=-2.(-a)=\sqrt{3}$
$a=\frac{\sqrt{3}}{2}$
Jawaban: C
Matematika IPA SBMPTN 2016 No. 15
Diketahui tiga bilangan positif $^{2}\log a$, $^{2}\log b$, $^{2}\log c$ membentuk barisan aritmetika. Jika $abc=128$, maka suku kedua barisan tersebut adalah …
A. $\frac{4}{3}$
B. $\frac{7}{3}$
C. 2
D. 8
E. 16
Pembahasan:
Barisan Aritmetika:
$^{2}\log a$, $^{2}\log b$, $^{2}\log c$
$2{{U}_{2}}={{U}_{1}}+{{U}_{3}}$
${{2.}^{2}}\log b{{=}^{2}}\log a{{+}^{2}}\log c$
$^{2}\log {{b}^{2}}{{=}^{2}}\log ac$
${{b}^{2}}=ac$ kedua ruas kali dengan b
${{b}^{3}}=abc$
${{b}^{3}}=128\Leftrightarrow b={{2}^{\frac{7}{3}}}$
${{U}_{2}}{{=}^{2}}\log b{{=}^{2}}\log {{2}^{\frac{7}{3}}}=\frac{7}{3}$
Jawaban: B
Artikel Terkait:
|

Post a Comment for "Pembahasan Soal SBMPTN 2016 Matematika IPA"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.