Pembahasan Soal SIMAK UI 2014 Matematika Dasar Kode 511 (KD1)

Hm...! Dah lama juga nih tidak buat postingan pembahasan matematika. Hari ini saya coba luangkan waktu untuk membuat Pembahasan Matematika Dasar SIMAK UI 2014 Kode 511 (KD1). Jujur, menurut saya nih soal SIMAK UI tergolong soal yang lebih sulit dibandingkan soal SBMPTN, untuk itu juga dibutuhkan waktu dan fokus yang lebih tinggi lagi. Dan kita gak perlu kuatir, sebab pepatah mengatakan bahwa setumpul-tumpulnya pisau, jika sering di asah tentu akan tajam juga. Begitu juga kita sesulit-sulitnya soal SIMAK UI, jika sering dilatih, dipelajari tentu kita akan mahir juga menyelesaikannya. Di postingan ini juga saya sediakan link download soalnya, sehingga teman-teman bisa menjawabnya secara mandiri terlebih dahulu tanpa melihat pembahasan ini.

---

Matematika Dasar SIMAK UI 2014 No. 1
Jika $f(2)=3$, $f'(2)=6$, $g(2)=1$, $g'(2)=4$ dan $h(x)=\frac{f(x)g(x)}{f(x)-g(x)}$, maka $h'(2)$ = …
A. $\frac{15}{4}$   B. 6   C. $\frac{15}{2}$   D. 9   E. 12
Pembahasan:
Misalkan:
$u(x)=f(x).g(x)$
$u(2)=f(2).g(2)=3.1=3$
$u'(x)=f'(x).g(x)+f(x).g'(x)$
$u'(2)=f'(2).g(2)+f(2).g'(2)$
$u'(2)=6.1+3.4=18$
$v(x)=f(x)-g(x)$
$v(2)=f(2)-g(2)=3-1=2$
$v'(x)=f'(x)-g'(x)$
$v'(2)=f'(2)-g'(2)$
$v'(2)=6-4=2$
$h(x)=\frac{f(x)g(x)}{f(x)-g(x)}$
$h(x)=\frac{u(x)}{v(x)}$
$h'(x)=\frac{u'(x).v(x)-v'(x).u(x)}{{{\left( v(x) \right)}^{2}}}$
$h'(2)=\frac{u'(2).v(2)-v'(2).u'(2)}{{{\left( v(2) \right)}^{2}}}$
$h'(2)=\frac{18.2-2.3}{{{2}^{2}}}=\frac{30}{4}=\frac{15}{2}$
Jawaban: C

---

Matematika Dasar SIMAK UI 2014 No. 2

Misalkan $f(x)$ menunjukkan jumlah angka-angka dalam bilangan positif $x$. Sebagai contoh, $f(9)=9$ dan $f(78)=7+8=15$. Banyaknya bilangan $x$ yang terdiri dari 2 angka dan memenuhi $(f\circ f)(x)=3$ adalah …

A. 3   B. 4   C. 7   D. 9   E. 10

Pembahasan:

$(f\circ f)(x)=3\Leftrightarrow f(f(x))=3$

$x=12\Rightarrow f(f(12))=f(1+2)=f(3)=3$

$x=21\Rightarrow f(f(21))=f(2+1)=f(3)=3$

$x=30\Rightarrow f(f(3))=f(3+0)=f(3)=3$

$x=39\Rightarrow f(f(39))=f(3+9)=f(12)=3$

$x=48\Rightarrow f(f(48))=f(4+8)=f(12)=3$

$x=57\Rightarrow f(f(57))=f(5+7)=f(12)=3$

$x=66\Rightarrow f(f(66))=f(6+6)=f(12)=3$

$x=75\Rightarrow f(f(75))=f(7+5)=f(12)=3$

$x=84\Rightarrow f(f(84))=f(8+4)=f(12)=3$

$x=93\Rightarrow f(f(39))=f(9+3)=f(12)=3$

Jadi, banyak bilangan $x$ yang memenuhi adalah 10 bilangan.

Jawaban: E

---

Matematika Dasar SIMAK UI 2014 No. 3

Malik dan Ali melakukan permainan lempar anak panah. Malik melempar tepat sasaran dengan peluang 0,65, sedangkan Ali melempar tepat sasaran dengan peluang 0,45. Malik memenangkan permainan jika Malik melempar tepat sasaran dan Ali tidak mengenai sasaran. Sebaliknya, Ali menang jika Ali melempar tepat sasaran dan Malik tidak mengenai sasaran. Kondisi lainnya adalah permainan seri. Peluang bahwa permainan akan berakhir seri adalah …

A. 0,4850

B. 0,2925

C. 0,2425

D. 0,2275

E. 0,1925

Pembahasan:

$P({{A}^{c}})=1-P(A)$

$P(M)$ = peluang Malik tepat sasaran = 0,65

$P({{M}^{c}})$ = peluang Malik tidak tepat sasaran = 0,35

$P(A)$ = peluang Ali tepat sasaran = 0,45

$P({{A}^{c}})$ = peluang Ali tidak tepat sasaran = 0,55

Agar permainan berakhir seri maka ada 2 kemungkinan:

Pertama: Ali dan Malik melempar tepat sasaran.

${{P}_{1}}=P(A)\times P(M)$ = 0,45 x 0,65 = 0,2925

Kedua: Ali dan Malik tidak mengenai sasaran.

${{P}_{2}}=P({{A}^{c}})\times P({{M}^{c}})$ = 0,55 x 0,35 = 0,1925

$P={{P}_{1}}+{{P}_{2}}$ = 0,2925 + 0,1925 = 0,4850

Jawaban: A

---

Matematika Dasar SIMAK UI 2014 No. 4

Terdapat 2 kotak yang masing-masing berisi bola hitam dan bola putih, dan banyaknya bola pada kedua kotak adalah 20. Sebuah bola diambil dari masing-masing kotak dan peluang bahwa kedua bola berwarna hitam adalah $\frac{5}{12}$, dan peluang bahwa kedua bola berwarna putih adalah $\frac{m}{n}$ dengan $m$ dan $n$ adalah bilangan bulat positif terkecil yang mungkin. Nilai $m+n$ adalah …

A. 13   B. 14   C. 15   D. 16   E. 22

Pembahasan:

Misalkan:

Kotak A berisi sebanyak a bola dengan p hitam dan a-p putih.

Kotak B berisi sebanyak b bola dengan q hitam dan b-q putih.

a + b = 20 bola

P(terambil 1 hitam dari kotak A dan 1 hitam dari kotak B) = $\frac{5}{12}$

$\frac{_{p}{{C}_{1}}}{_{a}{{C}_{1}}}\times \frac{_{q}{{C}_{1}}}{_{b}{{C}_{1}}}=\frac{5}{12}$

$\frac{p}{a}\times \frac{q}{b}=\frac{5}{12}$

Karena a + b = 20, maka ada 3 kemungkinan:

$\frac{p}{a}\times \frac{q}{b}=\frac{10}{12}\times \frac{4}{8}=\frac{15}{18}\times \frac{1}{2}=\frac{5}{8}\times \frac{8}{12}$

Kemungkinan I:

$\frac{p}{a}\times \frac{q}{b}=\frac{10}{12}\times \frac{4}{8}$

Artinya pada kotak A berisi 10 bola hitam dan 2 bola putih, sedangkan pada kotak B berisi 4 bola hitam dan 4 bola putih. Jadi, peluang kedua bola berwarna putih adalah:

$\frac{m}{n}=\frac{2}{12}\times \frac{4}{8}=\frac{1}{12}\Leftrightarrow m+n=13$

Kemungkinan II:

$\frac{p}{a}\times \frac{q}{b}=\frac{15}{18}\times \frac{1}{2}$

Artinya pada kotak A berisi 15 bola hitam dan 3 bola putih, sedangkan pada kotak B berisi 1 bola hitam dan 1 bola putih. Jadi, peluang kedua bola berwarna putih adalah:

$\frac{m}{n}=\frac{3}{18}\times \frac{1}{2}=\frac{1}{12}\Leftrightarrow m+n=13$

Kemungkinan III:

$\frac{p}{a}\times \frac{q}{b}=\frac{5}{8}\times \frac{8}{12}$

Artinya pada kotak A berisi 5 bola hitam dan 3 bola putih, sedangkan pada kotak B berisi 8 bola hitam dan 4 bola putih. Jadi, peluang kedua bola berwarna putih adalah:

$\frac{p}{a}\times \frac{q}{b}=\frac{3}{8}\times \frac{4}{12}=\frac{1}{8}\Leftrightarrow m+n=9$

Jadi, nilai minimum m + n = 9. Namun, karena di opsi tidak ada 9 maka pilihannya adalah A.

Jawaban: A

---

Matematika Dasar SIMAK UI 2014 No. 5

Sebuah himpunan yang terdiri atas 10 anggota yang semuanya bilangan bulat mempunyai rata-rata, median, modus serta jangkauan yang sama yaitu 9. Hasil kali antara bilangan terkecil dan terbesar yang masuk dalam himpunan tersebut adalah …

A. 90

B. 112

C. 126

D. 136

E. 162

Pembahasan:

Misalkan 10 data tersebut:

${{x}_{1}}\le {{x}_{2}}\le {{x}_{3}}\le {{x}_{4}}\le {{x}_{5}}\le {{x}_{6}}\le {{x}_{7}}\le {{x}_{8}}\le {{x}_{9}}\le {{x}_{10}}$

$\bar{x}=\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+...+{{x}_{10}}}{10}=9$

${{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}}+{{x}_{6}}+{{x}_{7}}+{{x}_{8}}+{{x}_{9}}+{{x}_{10}}=90$

$Me=\frac{{{x}_{5}}+{{x}_{6}}}{2}=9\Leftrightarrow {{x}_{5}}+{{x}_{6}}=18$

Mo = 9. Karena Modusnya = 9 maka ${{x}_{5}}={{x}_{6}}=9$

$J={{x}_{10}}-{{x}_{1}}=9\Leftrightarrow {{x}_{10}}={{x}_{1}}+9$

Sehingga kita peroleh batas nilai $0\le {{x}_{1}}\le 9$ dan setelah di cek  yang memenuhi $2\le {{x}_{1}}\le 7$. Untuk lebih jelasnya kita coba mendata beberapa kemungkinannya sebagai berikut:

Jawaban: B

---

Matematika Dasar SIMAK UI 2014 No. 6

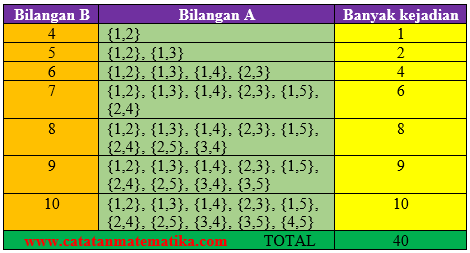
A memilih secara acak 2 bilangan yang berbeda dari {1, 2, 3, 4, 5} dan B secara acak memilih sebuah bilangan dari {1, 2, 3, …, 10}. Peluang bahwa bilangan B lebih besar dari jumlah 2 bilangan yang dipilih oleh A adalah …

A. $\frac{1}{5}$   B. $\frac{1}{3}$   C. $\frac{2}{5}$   D. $\frac{1}{2}$   E. $\frac{3}{5}$

Pembahasan:

n(A) = banyak cara A memilih 2 bilangan dari {1, 2, 3, 4, 5}

$n(A)={}_{5}{{C}_{2}}=\frac{5!}{2!.3!}=10$

n(B) = banyak cara B memilih 1 bilangan dari {1, 2, 3, …, 10}

$n(B)={}_{10}{{C}_{1}}=\frac{10!}{1!.9!}=10$

n(S) = n(A) x n(B) = 10x10 = 100

Untuk mempermudah maka kita tentukan dulu bilangan yang dipilih oleh si B, maka kita peroleh kemungkinan-kemungkinannya sebagai berikut:

Peluang bahwa bilangan B lebih besar dari jumlah 2 bilangan yang dipilih oleh A adalah:

= $\frac{40}{100}=\frac{2}{5}$ 

Jawaban: C

---

Matematika Dasar SIMAK UI 2014 No. 7

Jika A adalah invers dari matriks $\frac{1}{3}\left[ \begin{matrix}   -1 & -3  \\   4 & 5  \\ \end{matrix} \right]$, maka $A\left[ \begin{matrix}   x  \\   y  \\ \end{matrix} \right]=\left[ \begin{matrix}   1  \\   3  \\ \end{matrix} \right]$ akan menghasilkan nilai $x$ dan $y$ yang memenuhi $2x+y$ = …

A. $-\frac{10}{3}$   B. $-\frac{1}{3}$   C. 1   D. $\frac{9}{7}$   E. $\frac{20}{3}$

Pembahasan:

${{A}^{-1}}=\frac{1}{3}\left[ \begin{matrix}   -1 & -3  \\   4 & 5  \\ \end{matrix} \right]$

$A\left[ \begin{matrix}   x  \\   y  \\ \end{matrix} \right]=\left[ \begin{matrix}   1  \\   3  \\ \end{matrix} \right]$

$\left[ \begin{matrix}   x  \\   y  \\ \end{matrix} \right]={{A}^{-1}}.\left[ \begin{matrix}   1  \\   3  \\ \end{matrix} \right]$

$\left[ \begin{matrix}   x  \\   y  \\ \end{matrix} \right]=\frac{1}{3}\left[ \begin{matrix}   -1 & -3  \\   4 & 5  \\ \end{matrix} \right].\left[ \begin{matrix}   1  \\   3  \\ \end{matrix} \right]$

$\left[ \begin{matrix}   x  \\   y  \\ \end{matrix} \right]=\frac{1}{3}\left[ \begin{matrix}   -1-9  \\   4+15  \\ \end{matrix} \right]$

$\left[ \begin{matrix}   x  \\   y  \\ \end{matrix} \right]=\left[ \begin{matrix}   \frac{-10}{3}  \\   \frac{19}{3}  \\ \end{matrix} \right]$

$2x+y=2\left( \frac{-10}{3} \right)+\frac{19}{3}=-\frac{1}{3}$

Jawaban: B

---

Matematika Dasar SIMAK UI 2014 No. 8

Diketahui untuk $n > 1$, berlaku ${{s}_{n}}=\frac{1}{{{2}^{n}}}+\frac{1}{{{3}^{n}}}+\frac{1}{{{4}^{n}}}+...$ maka ${{s}_{2}}+{{s}_{3}}+{{s}_{4}}+...$ = …

A. 1   B. 2   C. $\pi $   D. ${{\pi }^{2}}$   E. $\infty $

Pembahasan:

${{s}_{n}}=\frac{1}{{{2}^{n}}}+\frac{1}{{{3}^{n}}}+\frac{1}{{{4}^{n}}}+...$

${{s}_{2}}=\frac{1}{{{2}^{2}}}+\frac{1}{{{3}^{2}}}+\frac{1}{{{4}^{2}}}+...$

${{s}_{3}}=\frac{1}{{{2}^{3}}}+\frac{1}{{{3}^{3}}}+\frac{1}{{{4}^{3}}}+...$

${{s}_{4}}=\frac{1}{{{2}^{4}}}+\frac{1}{{{3}^{4}}}+\frac{1}{{{4}^{4}}}+...$

….

Kita jumlahkan maka akan diperoleh deret geometri tak hingga sebagai berikut:

${{s}_{2}}+{{s}_{3}}+{{s}_{4}}+...$

= $\frac{1}{{{2}^{2}}}+\frac{1}{{{2}^{3}}}+\frac{1}{{{2}^{4}}}+...$ + $\frac{1}{{{3}^{2}}}+\frac{1}{{{3}^{3}}}+\frac{1}{{{3}^{4}}}+...$ + $\frac{1}{{{4}^{2}}}+\frac{1}{{{4}^{3}}}+\frac{1}{{{4}^{4}}}+...$ + …

= $\frac{\frac{1}{4}}{1-\frac{1}{2}}+\frac{\frac{1}{9}}{1-\frac{1}{3}}+\frac{\frac{1}{16}}{1-\frac{1}{4}}+...$ 

= $\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...$

= $\frac{1}{1\times 2}+\frac{1}{2\times 3}+\frac{1}{3\times 4}+...$

= $\left( \frac{1}{1}-\frac{1}{2} \right)+\left( \frac{1}{2}-\frac{1}{3} \right)+\left( \frac{1}{3}-\frac{1}{4} \right)+...$

= 1

Jawaban: A

---

Matematika Dasar SIMAK UI 2014 No. 9

Diketahui deret aritmetika terdiri dari $n$ suku. Suku awal deret tersebut merupakan jumlah $n$ suku pertama bilangan genap dan bedanya $n$, maka jumlah deret aritmetika tersebut adalah …

A. ${{n}^{3}}$

B. $\frac{{{n}^{3}}}{2}$

C. $\frac{3{{n}^{3}}}{2}+\frac{{{n}^{2}}}{2}$

D. $\frac{3{{n}^{3}}}{2}-\frac{{{n}^{2}}}{2}$

E. ${{n}^{2}}$

Pembahasan:

Barisan Aritmetika:

a = jumlah n suku pertama bilangan genap

a = n(n + 1)

b = n

maka jumlah deret:

${{S}_{n}}=\frac{n}{2}\left[ 2a+(n-1)b \right]$

${{S}_{n}}=\frac{n}{2}\left[ 2n(n+1)+(n-1)n \right]$

${{S}_{n}}=\frac{n}{2}\left[ 2{{n}^{2}}+2n+{{n}^{2}}-n \right]$

${{S}_{n}}=\frac{n}{2}\left[ 3{{n}^{2}}+n \right]$

${{S}_{n}}=\frac{3{{n}^{3}}}{2}+\frac{{{n}^{2}}}{2}$

Jawaban: C

---

Matematika Dasar SIMAK UI 2014 No. 10

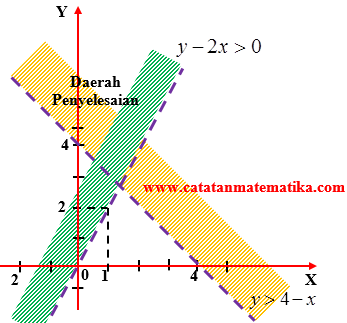
Himpunan titik-titik yang memenuhi pertidaksamaan $y-2x > 0$ dan $y > 4-x$ seluruhnya berada di kuadran …

A. I

B. I dan II

C. I dan IV

D. I, II, dan III

E. I, III, dan IV

Pembahasan:

Jadi, daerah penyelesaian berada di kuadran I dan II.

Jawaban: B

---

Matematika Dasar SIMAK UI 2014 No. 11

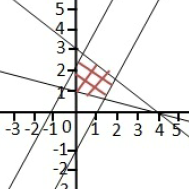
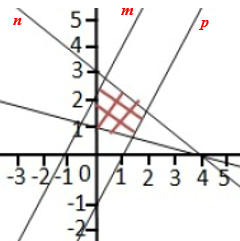
Diberikan grafik dari sistem suatu pertidaksamaan linear seperti gambar di atas. Koordinat (x,y) dari titik-titik yang berada pada daerah yang diarsir memenuhi pertidaksamaan …

A. $x\ge 0$, $y\ge 0$, $2x-y\ge -2$, $3x+4y\le 12$, $-x+y\ge -1$

B. $x\ge 0$, $y\ge 0$, $2x-y\ge -2$, $3x+4y\ge 12$, $-x+y\le -1$

C. $x\ge 0$, $y\ge 0$, $2x-y\ge -2$, $3x+4y\le 12$, $-x+y\le -1$

D. $x\ge 0$, $y\ge 0$, $2x-y\le -2$, $3x+4y\le 12$, $x-y\le 1$

E. $x\ge 0$, $y\ge 0$, $2x-y\le -2$, $3x+4y\le 12$, $x-y\ge 1$

Pembahasan:

Perhatikan gambar berikut ini.

Dari gambar terlihat bahwa daerah arsir berada di kuadran I, maka $x\ge 0$ dan $y\ge 0$.

Perhatikan garis m melalui titik (0,2) dan (-1,0) maka pertidaksamaan garis m adalah $2x-y\ge -2$.

Perhatikan garis n melalui titik (0,3) dan (4,0) maka pertidaksamaan garis n adalah $3x+4y\le 12$.

Perhatikan garis p melalui titik (0,-1) dan (1,0) maka pertidaksamaan garis p adalah $-x+y\ge -1$.

Jawaban: A

---

Matematika Dasar SIMAK UI 2014 No. 12

Himpunan penyelesaian $x$ yang memenuhi pertidaksamaan $4-3x\le {{x}^{2}}-4x\le 2+6x\le 5$ adalah …

A. $\left\{ x\in R|x\le \frac{1-\sqrt{17}}{2} \right.$ atau $\left. x\ge \frac{1+\sqrt{17}}{2} \right\}$

B. $\left\{ x\in R|x\le \frac{1}{2} \right\}$

C. $\left\{ x\in R|\frac{1}{2}\le x\le \frac{1+\sqrt{17}}{2} \right\}$

D. $\left\{ x\in R|5-3\sqrt{3}\le x\le \frac{1}{2} \right\}$

E. $\left\{ x\in R|5-3\sqrt{3}\le x\le 5+3\sqrt{3} \right\}$

Pembahasan:

$4-3x\le {{x}^{2}}-4x\le 2+6x\le 5$

1) $4-3x\le {{x}^{2}}-4x$

${{x}^{2}}-x-4\ge 0$

$x=\frac{1\pm \sqrt{{{(-1)}^{2}}-4.1.(-4)}}{2.1}$

$x=\frac{1\pm \sqrt{17}}{2}$

$\frac{1-\sqrt{17}}{2}\le x\le \frac{1+\sqrt{17}}{2}$

2) $4-3x\le 2+6x$

$-9x\le -2\Leftrightarrow x\ge \frac{2}{9}$

3) $4-3x\le 5\Leftrightarrow x\ge -\frac{1}{3}$

4) ${{x}^{2}}-4x\le 2+6x$

${{x}^{2}}-10x-2\le 0$

$x=\frac{10\pm \sqrt{108}}{2}$

$x=\frac{10\pm 6\sqrt{3}}{2}=5\pm 3\sqrt{3}$

$5-3\sqrt{3}\le x\le 5+3\sqrt{3}$

5) ${{x}^{2}}-4x\le 5$

${{x}^{2}}-4x-5\le 0$

$(x-5)(x-1)\le 0$

$1\le x\le 5$

6) $2+6x\le 5\Leftrightarrow x\le \frac{1}{2}$

Himpunan penyelesaian adalah irisan dari 1), 2), 3), 4), 5) dan 6)

yaitu himpunan kosong.

Jawaban: Opsi Tidak Ada

---

Matematika Dasar SIMAK UI 2014 No. 13

Jika $x$ dan $y$ memenuhi $2{{y}^{2}}-1 > x$ dan $9y-x+4=0$, maka $x-y$ memenuhi …

A. $0 < x-y < 44$

B. $-\frac{1}{2} < x-y < 49$

C. $x-y < -\frac{11}{2}$ atau $x-y>\frac{99}{2}$

D. $x-y < 0$ atau $x-y > 44$

E. $-\frac{1}{2} < x-y < 44$ 

Pembahasan:

$9y-x+4=0 \Leftrightarrow x=9y+4$

$2{{y}^{2}}-1 > x$

$2{{y}^{2}}-1 > 9y+4$

$2{{y}^{2}}-9y-5 > 0$

$(2y+1)(y-5) > 0$

$y < -\frac{1}{2}$ atau $y > 5$

Substistusi ke:

$9y-x+4=0$

$y-x=-4-8y$

$x-y=4+8y$

Untuk $y < -\frac{1}{2}$ maka:

$x-y < 4+8.\left( -\frac{1}{2} \right)$

$x-y < 0$

Untuk $y > 5$ maka:

$x-y > 4+8.5$

$x-y > 44$

Jawaban: D

---

Matematika Dasar SIMAK UI 2014 No. 14

Diketahui untuk bilangan real positif a, b, c, p, q, dan r berlaku $\frac{a}{p}=\frac{b}{q}=\frac{c}{r}$. Nilai dari $\frac{abc(p+q)(q+r)(r+p)}{pqr(a+b)(b+c)(c+a)}$ adalah …

A. 0

B. $\frac{1}{3}$

C. 1

D. 3

E. tergantung pada nilai $\frac{a}{p}=\frac{b}{q}=\frac{c}{r}$ 

Pembahasan:

Untuk mempermudah kita anggap saja bilangannya sebagai berikut:

$\frac{a}{p}=\frac{b}{q}=\frac{c}{r}=\frac{1}{3}=\frac{2}{6}=\frac{3}{9}$

a = 1, b = 2, c = 3, p = 3, q = 6 , r = 9

maka:

$\frac{abc(p+q)(q+r)(r+p}{pqr(a+b)(b+c)(c+a)}$

$=\frac{1.2.3(3+6)(6+9)(9+3)}{3.6.9(1+2)(2+3)(3+1)}$

$=\frac{1.2.3.9.15.12}{3.6.9.3.5.4}=1$

Jawaban: C

---

Matematika Dasar SIMAK UI 2014 No. 15

Jika diketahui $x < 0$, maka banyaknya penyelesaian yang memenuhi sistem persamaan:

$\left\{ \begin{matrix}   {{x}^{2}}-ax+2014=0  \\   {{x}^{2}}-2014x+a=0  \\ \end{matrix} \right.$ 

adalah …

A. 0   B. 1   C. 2   D. 3   E. 4

Pembahasan:

${{x}^{2}}-ax+2014=0$

${{x}^{2}}-2014x+a=0$

---------------------- (-)

$(-a+2014)x+2014-a=0$

$(-a+2014)x=a-2014$

$x=\frac{a-2014}{2014-a}=-1$

Banyak penyelesaiannya adalah 1.

Jawaban: B

---

Matematika Dasar SIMAK UI 2014 No. 16

Diketahui persamaan kuadrat $f(x)=a{{x}^{2}}+bx+c$, a, b, c, adalah bilangan bulat tidak nol. Pernyataan berikut yang tidak mungkin terjadi adalah …

A. f(x) memiliki dua akar rasional.

B. f(x) memiliki hanya satu akar rasional.

C. f(x) tidak memiliki akar bilangan real.

D. f(x) memiliki hanya satu akar negatif.

E. f(x) memiliki hanya satu akar irrasional.

Pembahasan:

$f(x)=a{{x}^{2}}+bx+c$

Sifat-sifat persamaan kuadrat:

1. Jika $D > 0$ dan $D={{k}^{2}}$ = bilangan kuadrat maka persamaan kuadrat memiliki 2 akar rasional (opsi A).

2. Jika $D = 0$ maka memiliki 1 akar rasional (opsi B).

3. Jika $D < 0$ maka tidak memiliki akar real (opsi C).

4. Jika $D > 0$, $c < 0$, $a > 0$ maka memiliki satu akar negatif (opsi D).

5. Jika $D > 0$, $D\ne {{k}^{2}}$ maka memiliki 2 akar irrasional (opsi E tidak terpenuhi).

Jawaban: E

---

Matematika Dasar SIMAK UI 2014 No. 17

Misalkan y adalah bilangan real sedemikian sehingga $3 < y < 4$ dan ${{y}^{3}}-6y-7=0$. Bilangan bulat terdekat dengan ${{y}^{2}}$ adalah …

A. 8   B. 7   C. 6   D. 3   E. 2

Pembahasan:

${{y}^{3}}-6y-7=0$

$y({{y}^{2}}-6)-7=0$

$y({{y}^{2}}-6)=7$

${{y}^{2}}=\frac{7}{y}+6$; karena $3 < y < 4$ maka:

$\frac{7}{4}+6 < {{y}^{2}} < \frac{7}{3}+6$

$\frac{31}{4} < {{y}^{2}} < \frac{25}{3}$

$7,75 < {{y}^{2}} < 8,333$

Bilangan bulat terdekat dengan ${{y}^{2}}$ adalah 8.

Jawaban: A

---

Matematika Dasar SIMAK UI 2014 No. 18

Jika $^{ab}\log a=4$, maka $^{ab}\log \frac{\sqrt[3]{a}}{\sqrt{b}}$ = …

A. -3   B. $-\frac{3}{4}$   C. $-\frac{1}{6}$   D. $\frac{29}{42}$   E. $\frac{17}{6}$

Pembahasan:

$^{ab}\log a=4$

$\frac{1}{^{a}\log ab}=4$

$\frac{1}{^{a}\log a{{+}^{a}}\log b}=4$

$\frac{1}{1{{+}^{a}}\log b}=4$

$4+{{4.}^{a}}\log b=1$

$^{a}\log b=-\frac{3}{4}$

$^{ab}\log \frac{\sqrt[3]{a}}{\sqrt{b}}$

${{=}^{ab}}\log \sqrt[3]{a}{{-}^{ab}}\log \sqrt{b}$

${{=}^{ab}}\log {{a}^{\frac{1}{3}}}{{-}^{ab}}\log {{b}^{\frac{1}{2}}}$

$=\frac{1}{3}{{.}^{ab}}\log a-\frac{1}{2}{{.}^{ab}}\log b$

$=\frac{1}{3}.4-\frac{1}{2}.\frac{1}{^{b}\log ab}$

$=\frac{4}{3}-\frac{1}{2}.\frac{1}{^{b}\log a{{+}^{b}}\log b}$

$=\frac{4}{3}-\frac{1}{2\left( -\frac{4}{3}+1 \right)}$

$=\frac{4}{3}+\frac{3}{2}=\frac{17}{6}$

Jawaban: E

---

Matematika Dasar SIMAK UI 2014 No. 19

Dalam basis 10, bilangan bulat positif p memiliki 3 digit, bilangan bulat positif q memiliki p digit, dan bilangan bulat positif r memiliki q digit. Nilai terkecil untuk r adalah …

A. ${{10}^{{{10}^{100}}}}$

B. ${{10}^{{{10}^{100}}-1}}$

C. ${{10}^{{{10}^{99}}}}$

D. ${{10}^{{{10}^{99}}-1}}$

E. ${{10}^{{{99}^{99}}}}$

Pembahasan:

Untuk memperoleh nilai $r$ terkecil, maka nilai $p$ dan $q$  juga haruslah nilai terkecil.

$p$ adalah bilangan bulat positif terkecil, 3 digit maka $p=100$.

$q$ adalah bilangan bulat positif terkecil, 100 digit maka $q={{10}^{100-1}}={{10}^{99}}$.

$r$ adalah bilangan bulat positif terkecil, ${{10}^{99}}$ digit maka $r={{10}^{{{10}^{99}}-1}}$.

Jawaban: D

---

Matematika Dasar SIMAK UI 2014 No. 20

Gunakan Petunjuk C dalam menjawab soal nomor 20.

Jika ${{f}^{-1}}\left( \frac{1-x}{1+x} \right)=x$ untuk semua $x\ne -1$, maka pernyataan berikut yang terpenuhi adalah …

(1) $f(-2-x)=-2-f(x)$

(2) $f(-x)=\frac{1}{f(x)},x\ne 1$ 

(3) $f\left( \frac{1}{x} \right)=-f(x),x\ne 0$

(4) $f(f(x))=-x$ 

Pembahasan:

${{f}^{-1}}\left( \frac{1-x}{1+x} \right)=x\Leftrightarrow f(x)=\frac{1-x}{1+x}$

Pernyataan 1:

$f(-2-x)=-2-f(x)$

$\frac{1-(-2-x)}{1+(-2-x)}=-2-\frac{1-x}{1+x}$

$\frac{3+x}{-1-x}=\frac{-2(1+x)}{1+x}-\frac{1-x}{1+x}$

$\frac{-3-x}{1+x}=\frac{-3-x}{1+x}$ (BENAR)

Pernyataan 2:

$f(-x)=\frac{1}{f(x)},x\ne 1$

$\frac{1+x}{1-x}=\frac{1}{\frac{1-x}{1+x}}$

$\frac{1+x}{1-x}=\frac{1+x}{1-x}$ (BENAR)

Pernyataan 3:

$f\left( \frac{1}{x} \right)=-f(x),x\ne 0$

$\frac{1-\frac{1}{x}}{1+\frac{1}{x}}=-\frac{1-x}{1+x}$

$\frac{x-1}{x+1}=\frac{x-1}{x+1}$ (BENAR)

Pernyataan 4:

$f\left( \frac{1-x}{1+x} \right)=-x$

$\frac{1-\frac{1-x}{1+x}}{1+\frac{1-x}{1+x}}=-x$

$\frac{\frac{1+x}{1+x}-\frac{1-x}{1+x}}{\frac{1+x}{1+x}+\frac{1-x}{1+x}}=-x$

$\frac{\frac{2x}{1+x}}{\frac{2}{1+x}}=-x$

$x=-x$ (SALAH)

Jawaban: A

---

Artikel Terkait:

Soal dan Pembahasan Matematika Dasar SIMAK UI 2015. Soal dan Pembahasan Matematika Dasar SIMAK UI 2013. Soal dan Pembahasan Matematika Dasar SIMAK UI 2012.

Semoga postingan: Pembahasan Soal SIMAK UI 2014 Matematika Dasar Kode 511 (KD1) ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :