Pembahasan Soal SIMAK UI 2016 Matematika Dasar
SIMAK UI 2016-Saya kehabisan kata-kata nih buat pengantar postingan ini, hehehe....! So... To the point aja ya..! Berikut ini adalah Soal dan Pembahasan Matematika Dasar (TKPA) SIMAK UI 2016, seperti biasa b4ngrp selalu menyertakan soal dalam bentuk file yang dapat di download dan diprint sepuasnya. Ingat, berusahalah terlebih dahulu menjawab soal-soal tersebut dengan mandiri. Abis tuh bolehlah di intip-intip pembahasannya disini untuk mencocokkan jawaban kalian ya..! Oh iya, jika pada pembahasan ini ada yang kurang tepat mohon dikoreksi melalui kolom komentar ya...! Dan yang paling penting supaya b4ngrp tetap semangat mengembangkan blog ini, mohon bantuannya untuk share postingan ini ya..! Terima kasih.
Matematika Dasar SIMAK UI 2016 No. 1
Bentuk sederhana dari ekspresi $\sqrt[3]{4}{{\left( \sqrt[3]{\frac{9}{16}}-\sqrt[3]{\frac{3}{16}}+\sqrt[3]{\frac{1}{16}} \right)}^{-1}}$ adalah …
A. $\sqrt[3]{4}+1$
B. $\frac{\sqrt[3]{4}+1}{\sqrt[3]{3}}$
C . $\sqrt[3]{3}+1$
D. $\frac{\sqrt[3]{3}+1}{\sqrt[3]{4}}$
E. $\frac{\sqrt[3]{3}+1}{4}$
Pembahasan:
$\sqrt[3]{4}{{\left( \sqrt[3]{\frac{9}{16}}-\sqrt[3]{\frac{3}{16}}+\sqrt[3]{\frac{1}{16}} \right)}^{-1}}$
= $\frac{\sqrt[3]{4}}{\sqrt[3]{\frac{9}{16}}-\sqrt[3]{\frac{3}{16}}+\sqrt[3]{\frac{1}{16}}}$
= $\frac{\sqrt[3]{4}}{\frac{\sqrt[3]{9}-\sqrt[3]{3}+\sqrt[3]{1}}{\sqrt[3]{16}}}$
= $\sqrt[3]{4}\times \frac{\sqrt[3]{16}}{\sqrt[3]{9}-\sqrt[3]{3}+\sqrt[3]{1}}$
= $\frac{\sqrt[3]{64}}{\sqrt[3]{9}-\sqrt[3]{3}+\sqrt[3]{1}}$
= $\frac{4}{\sqrt[3]{9}-\sqrt[3]{3}+1}\times \frac{\sqrt[3]{3}+1}{\sqrt[3]{3}+1}$
= $\frac{4\left( \sqrt[3]{3}+1 \right)}{3+\sqrt[3]{9}-\sqrt[3]{9}-\sqrt[3]{3}+\sqrt[3]{3}+1}$
= $\frac{4\left( \sqrt[3]{3}+1 \right)}{4}$
= $\sqrt[3]{3}+1$
Jawaban: C


Matematika Dasar SIMAK UI 2016 No. 1
Bentuk sederhana dari ekspresi $\sqrt[3]{4}{{\left( \sqrt[3]{\frac{9}{16}}-\sqrt[3]{\frac{3}{16}}+\sqrt[3]{\frac{1}{16}} \right)}^{-1}}$ adalah …
A. $\sqrt[3]{4}+1$
B. $\frac{\sqrt[3]{4}+1}{\sqrt[3]{3}}$
C . $\sqrt[3]{3}+1$
D. $\frac{\sqrt[3]{3}+1}{\sqrt[3]{4}}$
E. $\frac{\sqrt[3]{3}+1}{4}$
Pembahasan:
$\sqrt[3]{4}{{\left( \sqrt[3]{\frac{9}{16}}-\sqrt[3]{\frac{3}{16}}+\sqrt[3]{\frac{1}{16}} \right)}^{-1}}$
= $\frac{\sqrt[3]{4}}{\sqrt[3]{\frac{9}{16}}-\sqrt[3]{\frac{3}{16}}+\sqrt[3]{\frac{1}{16}}}$
= $\frac{\sqrt[3]{4}}{\frac{\sqrt[3]{9}-\sqrt[3]{3}+\sqrt[3]{1}}{\sqrt[3]{16}}}$
= $\sqrt[3]{4}\times \frac{\sqrt[3]{16}}{\sqrt[3]{9}-\sqrt[3]{3}+\sqrt[3]{1}}$
= $\frac{\sqrt[3]{64}}{\sqrt[3]{9}-\sqrt[3]{3}+\sqrt[3]{1}}$
= $\frac{4}{\sqrt[3]{9}-\sqrt[3]{3}+1}\times \frac{\sqrt[3]{3}+1}{\sqrt[3]{3}+1}$
= $\frac{4\left( \sqrt[3]{3}+1 \right)}{3+\sqrt[3]{9}-\sqrt[3]{9}-\sqrt[3]{3}+\sqrt[3]{3}+1}$
= $\frac{4\left( \sqrt[3]{3}+1 \right)}{4}$
= $\sqrt[3]{3}+1$
Jawaban: C
Matematika Dasar SIMAK UI 2016 No. 2
Jika $a$, $b$, dan $x$ bilangan real positif yang berbeda dengan 1 dan ${}^{a}\log x$ bilangan rasional, maka $9{{\left( {}^{a}\log x \right)}^{2}}+8{{\left( {}^{b}\log x \right)}^{2}}=18\left( {}^{a}\log x \right)\left( {}^{b}\log x \right)$ berlaku …
A. untuk semua nilai $a$, $b$, dan $x$.
B. jika dan hanya jika ${{a}^{2}}={{b}^{3}}$.
C. jika dan hanya jika ${{a}^{3}}={{b}^{4}}$
D. jika dan hanya jika ${{a}^{3}}={{b}^{2}}$ atau ${{a}^{3}}={{b}^{4}}$.
E. jika dan hanya jika ${{a}^{2}}={{b}^{3}}$ atau ${{a}^{4}}={{b}^{3}}$.
Pembahasan:
Misal: ${}^{a}\log x=p$ dan ${}^{b}\log x=q$ maka:
$9{{\left( {}^{a}\log x \right)}^{2}}+8{{\left( {}^{b}\log x \right)}^{2}}=18\left( {}^{a}\log x \right)\left( {}^{b}\log x \right)$
$9{{p}^{2}}+8{{q}^{2}}=18pq$
$9{{p}^{2}}-18pq+8{{q}^{2}}=0$
$9{{p}^{2}}-18pq+8{{q}^{2}}=0$
$(3p-2q)(3p-4q)=0$
$3p=2q$ atau $3p=4q$
*) Untuk $3p=2q$
$3.{}^{a}\log x=2.{}^{b}\log x$
${}^{{{a}^{\frac{1}{3}}}}\log x={}^{{{b}^{\frac{1}{2}}}}\log x$
${{a}^{\frac{1}{3}}}={{b}^{\frac{1}{2}}}$
${{\left( {{a}^{\frac{1}{3}}} \right)}^{6}}={{\left( {{b}^{\frac{1}{2}}} \right)}^{6}}\Leftrightarrow {{a}^{2}}={{b}^{3}}$
*) Untuk $3p=4q$
$3.{}^{a}\log x=4.{}^{b}\log x$
${}^{{{a}^{\frac{1}{3}}}}\log x={}^{{{b}^{\frac{1}{4}}}}\log x$
${{a}^{\frac{1}{3}}}={{b}^{\frac{1}{4}}}$
${{\left( {{a}^{\frac{1}{3}}} \right)}^{12}}={{\left( {{b}^{\frac{1}{4}}} \right)}^{12}}\Leftrightarrow {{a}^{4}}={{b}^{3}}$
Jawaban: E
Matematika Dasar SIMAK UI 2016 No. 3
Jika akar ${{x}^{2}}+ax+b=0$ adalah $\frac{1}{3}$ kali akar ${{x}^{2}}+cx+a=0$ dengan $a,b,c\ne 0$, maka $\frac{a+c}{b}$ = …
A. $\frac{10}{27}$ B. $\frac{28}{9}$ C. 30 D. 36 E. 40
Pembahasan:
${{x}^{2}}+ax+b=0$ akar-akarnya ${{x}_{1}}$ dan ${{x}_{2}}$ maka:
${{x}_{1}}+{{x}_{2}}=-a$
${{x}_{1}}.{{x}_{2}}=b$
${{x}^{2}}+cx+a=0$ akar-akarnya ${{x}_{1}}$ dan ${{x}_{2}}$ maka:
${{x}_{3}}+{{x}_{4}}=-c$
${{x}_{3}}.{{x}_{4}}=a$
akar ${{x}^{2}}+ax+b=0$ adalah $\frac{1}{3}$ kali akar ${{x}^{2}}+cx+a=0$ maka:
${{x}_{1}}=\frac{1}{3}{{x}_{3}}$ dan ${{x}_{2}}=\frac{1}{3}{{x}_{4}}$
${{x}_{1}}+{{x}_{2}}=\frac{1}{3}{{x}_{3}}+\frac{1}{3}{{x}_{4}}$
${{x}_{1}}+{{x}_{2}}=\frac{1}{3}({{x}_{3}}+{{x}_{4}})$
$-a=\frac{1}{3}(-c)\Leftrightarrow c=3a$
${{x}_{1}}.{{x}_{2}}=\frac{1}{3}{{x}_{3}}.\frac{1}{3}{{x}_{4}}$
${{x}_{1}}.{{x}_{2}}=\frac{1}{9}{{x}_{3}}.{{x}_{4}}$
$b=\frac{1}{9}a\Leftrightarrow a=9b$
$\frac{a+c}{b}=\frac{9b+3a}{b}=\frac{9b+3.9b}{b}=36$
Jawaban: D
Matematika Dasar SIMAK UI 2016 No. 4
Diketahui bahwa $c$ dan $d$ solusi ${{x}^{2}}+ax+b=0$, $a$ dan $b$ solusi ${{x}^{2}}+cx+d=0$ dengan nilai $a$, $b$, $c$, dan $d$ bilangan real bukan nol. Nilai $a+b+c+d$ = …
A. -2 B. -1 C. 1 D. 2 E. 3
Pembahasan:
${{x}^{2}}+ax+b=0$ dan ${{x}^{2}}+cx+d=0$ maka:
${{x}^{2}}+ax+b={{x}^{2}}+cx+d$
$ax+b=cx+d$
$a=c$ dan $b=d$
${{x}^{2}}+ax+b=0$ akar-akarnya c dan d maka:
$c+d=-a$
$a+d=-a\Leftrightarrow d=-2a$
$c.d=b\Leftrightarrow c.b=b\Leftrightarrow c=1=a$
$d=-2a\Leftrightarrow d=-2.1=b\Leftrightarrow b=d=-2$
$a+b+c+d=1+(-2)+1+(-2)=-2$
Jawaban: A
Matematika Dasar SIMAK UI 2016 No. 5
Jika $x$ memenuhi $\frac{-3x+1}{{{x}^{2}}-6x-16}\ge 0$, maka nilai $y=-\frac{2}{x}+1$ terletak pada ….
A. $-5\le y < \frac{3}{4}$ atau $1 < y < 2$
B. $-5\le y < 1$ atau $y > 2$
C. $y\le -3$ atau $y > \frac{3}{4}$
D. $-5\le y < \frac{3}{4}$
E. $-5\le y < 2$
Pembahasan:
$\frac{-3x+1}{{{x}^{2}}-6x-16}\ge 0$
$\frac{-3x+1}{(x-8)(x+2)}\ge 0$
Nilai $x$ pembuat nol:
*) $-3x+1=0\Leftrightarrow x=\frac{1}{3}$
*) $x-8\ne 0\Leftrightarrow x\ne 8$
*) $x+2\ne 0\Leftrightarrow x\ne -2$

1) Untuk $x < -2$ maka:
$y=-\frac{2}{x}+1\Leftrightarrow 1 < y < -\frac{2}{-2}+1\Leftrightarrow 1 < y < 2$
2) Untuk $\frac{1}{3}\le x < 8$ maka:
$-\frac{2}{x}+1\le y < -\frac{2}{x}+1$
$-\frac{2}{\frac{1}{3}}+1\le y < -\frac{2}{8}+1$
$-5\le y < \frac{3}{4}$
Dari 1) dan 2) maka diperoleh: $-5\le y < \frac{3}{4}$ atau $1 < y < 2$
Jawaban: A
Matematika Dasar SIMAK UI 2016 No. 6
Diberikan tiga sistem pertidaksamaan linear berikut:
I. $x+y\le 3$, $2x+y\le 2$, $x\ge 0$, $y\ge 0$;
II. $2x+3y\le 6$, $3x+2y\le 6$, $x\ge 0$, $y\ge 0$;
III. $x+y\le 3$, $3x+2y\ge 6$, $x\ge 0$, $y\ge 0$;
Jika $a$, $b$, dan $c$ berturut-turut adalah banyak pasangan bilangan bulat $(x,y)$ yang memenuhi sistem I, II, dan III maka …
A. $a < b < c$
B. $a < c < b$
C. $b < a < c$
D. $c < b < a$
E. $c < a < b$
Pembahasan:
I. $x+y\le 3$, $2x+y\le 2$, $x\ge 0$, $y\ge 0$
nilai $(x,y)$ = {(0,0), (0,1), (0,2), (1,0)} maka a = 4
II. $2x+3y\le 6$, $3x+2y\le 6$, $x\ge 0$, $y\ge 0$;
nilai $(x,y)$ = {(0,0), (0,1), (0,2), (1,0), (2,0), (1,1)} maka b = 6
III. $x+y\le 3$, $3x+2y\ge 6$, $x\ge 0$, $y\ge 0$;
nilai $(x,y)$ = {(0,3), (1,2),(2,0),(2,1),(3,0)} maka c = 5
$4 < 5 < 6 \Leftrightarrow a < c < b$
Jawaban: B
Matematika Dasar SIMAK UI 2016 No. 7
Nilai dari $1+2.2+{{3.2}^{2}}+{{4.2}^{3}}+...+{{2016.2}^{2015}}$ adalah …
A. ${{2016.2}^{2015}}$
B. ${{2016.2}^{2015}}+1$
C. ${{2015.2}^{2016}}$
D. ${{2015.2}^{2016}}+1$
E. ${{2015.2}^{2016}}-1$
Pembahasan:
Teori:
$1.2+{{2.2}^{2}}+{{3.2}^{3}}+...+n{{.2}^{n}}=2\left[ 1+(n-1){{.2}^{n}} \right]$
$1+2.2+{{3.2}^{2}}+{{4.2}^{3}}+...+{{2016.2}^{2015}}$
= $\frac{2}{2}.\left( 1+2.2+{{3.2}^{2}}+{{4.2}^{3}}+...+{{2016.2}^{2015}} \right)$
= $\frac{1}{2}\left( 1.2+{{2.2}^{2}}+{{3.2}^{3}}+{{4.2}^{4}}+...+{{2016.2}^{2016}} \right)$
= $\frac{1}{2}.2\left[ 1+(2016-1){{.2}^{2016}} \right]$
= $1+{{2015.2}^{2016}}$
= ${{2015.2}^{2016}}+1$
Jawaban: D
Matematika Dasar SIMAK UI 2016 No. 8
Jika $A=\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]$, maka ${{A}^{2016}}$ = …
A. $\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
B. $\left[ \begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
C. $\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
D. $\left[ \begin{matrix} 0 & 2016 & 5 \\ 0 & 0 & 2016 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
E. $\left[ \begin{matrix} 0 & 1 & {{5}^{2016}} \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
Pembahasan:
$A=\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
${{A}^{2}}=\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right].\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]=\left[ \begin{matrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
${{A}^{3}}=\left[ \begin{matrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right].\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]=\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
Misal: ${{A}^{2013}}=\left[ \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right]$ maka:
${{A}^{2016}}={{A}^{2013}}.{{A}^{3}}$
${{A}^{2016}}=\left[ \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right].\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]=\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
Jawaban: A
Matematika Dasar SIMAK UI 2016 No. 9
Nilai $x$ didefinisikan sebagai angka terbesar yang muncul dari lemparan dua dadu bersamaan. Probabilitas mendapatkan nilai $x$ paling besar 3 adalah …
A. $\frac{1}{12}$ B. $\frac{1}{9}$ C. $\frac{1}{6}$ D. $\frac{1}{4}$ E. $\frac{1}{3}$
Pembahasan:
Pelemparan dua dadu bersamaan maka $n(S)=6\times 6=36$.
A = kejadian munculnya mata dadu paling besar 3
A = {(1,1), (1,2), (2,1), (1,3), (3,1), (2,2), (2,3), (3,2), (3,3)}
$n(A)=9$
$P(A)=\frac{n(A)}{n(S)}=\frac{9}{36}=\frac{1}{4}$
Jawaban: D
Matematika Dasar SIMAK UI 2016 No. 10
Jika $x+ay=b$, $2x+by=a$, dan $3x+aby=4$, maka $a+b$ = …
A. 0 B. 2 C. 4 D. 6 E. 8
Pembahasan:
$x+ay=b$
$2x+by=a$
------------------- (+)
$3x+(a+b)y=a+b$ …. Pers (4)
$3x+aby=4$ …. Pers (3)
Dari pers (4) dan (3) diperoleh $a+b=4$
Jawaban: C
Matematika Dasar SIMAK UI 2016 No. 11
Banyak susunan huruf berbeda yang dapat dibuat dari semua huruf pada kata SIMAK UI apabila huruf I harus selalu berdekatan adalah …
A. 432 B. 312 C. 240 D. 164 E. 120
Pembahasan:
karena huruf I harus selalu berdekatan, maka dapat anggap “I” adalah “satu” sehingga banyak huruf yang akan disusun adalah 6 (enam), maka diperoleh:
= 6 x 5 x 4 x 3 x 2 x 1 = 720 susunan.
Jawaban: (Tidak ada Opsi)
Matematika Dasar SIMAK UI 2016 No. 12
Lingkaran A, B, dan C saling bersinggungan satu sama lain menyinggung lingkaran D pada bagian dalam. Lingkaran B dan C berukuran sama dan lingkaran A memiliki jari-jari 1 serta melalui pusat lingkaran D. Jumlah luas lingkaran A, B, dan C adalah …
A. $\frac{64}{81}\pi $
B. $\frac{112}{81}\pi $
C. $\frac{189}{81}\pi $
D. $\frac{209}{81}\pi $
E. $\frac{225}{81}\pi $
Pembahasan:
Perhatikan gambar berikut!
Matematika Dasar SIMAK UI 2016 No. 6
Diberikan tiga sistem pertidaksamaan linear berikut:
I. $x+y\le 3$, $2x+y\le 2$, $x\ge 0$, $y\ge 0$;
II. $2x+3y\le 6$, $3x+2y\le 6$, $x\ge 0$, $y\ge 0$;
III. $x+y\le 3$, $3x+2y\ge 6$, $x\ge 0$, $y\ge 0$;
Jika $a$, $b$, dan $c$ berturut-turut adalah banyak pasangan bilangan bulat $(x,y)$ yang memenuhi sistem I, II, dan III maka …
A. $a < b < c$
B. $a < c < b$
C. $b < a < c$
D. $c < b < a$
E. $c < a < b$
Pembahasan:
I. $x+y\le 3$, $2x+y\le 2$, $x\ge 0$, $y\ge 0$
nilai $(x,y)$ = {(0,0), (0,1), (0,2), (1,0)} maka a = 4
II. $2x+3y\le 6$, $3x+2y\le 6$, $x\ge 0$, $y\ge 0$;
nilai $(x,y)$ = {(0,0), (0,1), (0,2), (1,0), (2,0), (1,1)} maka b = 6
III. $x+y\le 3$, $3x+2y\ge 6$, $x\ge 0$, $y\ge 0$;
nilai $(x,y)$ = {(0,3), (1,2),(2,0),(2,1),(3,0)} maka c = 5
$4 < 5 < 6 \Leftrightarrow a < c < b$
Jawaban: B
Matematika Dasar SIMAK UI 2016 No. 7
Nilai dari $1+2.2+{{3.2}^{2}}+{{4.2}^{3}}+...+{{2016.2}^{2015}}$ adalah …
A. ${{2016.2}^{2015}}$
B. ${{2016.2}^{2015}}+1$
C. ${{2015.2}^{2016}}$
D. ${{2015.2}^{2016}}+1$
E. ${{2015.2}^{2016}}-1$
Pembahasan:
Teori:
$1.2+{{2.2}^{2}}+{{3.2}^{3}}+...+n{{.2}^{n}}=2\left[ 1+(n-1){{.2}^{n}} \right]$
$1+2.2+{{3.2}^{2}}+{{4.2}^{3}}+...+{{2016.2}^{2015}}$
= $\frac{2}{2}.\left( 1+2.2+{{3.2}^{2}}+{{4.2}^{3}}+...+{{2016.2}^{2015}} \right)$
= $\frac{1}{2}\left( 1.2+{{2.2}^{2}}+{{3.2}^{3}}+{{4.2}^{4}}+...+{{2016.2}^{2016}} \right)$
= $\frac{1}{2}.2\left[ 1+(2016-1){{.2}^{2016}} \right]$
= $1+{{2015.2}^{2016}}$
= ${{2015.2}^{2016}}+1$
Jawaban: D
Matematika Dasar SIMAK UI 2016 No. 8
Jika $A=\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]$, maka ${{A}^{2016}}$ = …
A. $\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
B. $\left[ \begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
C. $\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
D. $\left[ \begin{matrix} 0 & 2016 & 5 \\ 0 & 0 & 2016 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
E. $\left[ \begin{matrix} 0 & 1 & {{5}^{2016}} \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
Pembahasan:
$A=\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
${{A}^{2}}=\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right].\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]=\left[ \begin{matrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
${{A}^{3}}=\left[ \begin{matrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right].\left[ \begin{matrix} 0 & 1 & 5 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{matrix} \right]=\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
Misal: ${{A}^{2013}}=\left[ \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right]$ maka:
${{A}^{2016}}={{A}^{2013}}.{{A}^{3}}$
${{A}^{2016}}=\left[ \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right].\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]=\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]$
Jawaban: A
Matematika Dasar SIMAK UI 2016 No. 9
Nilai $x$ didefinisikan sebagai angka terbesar yang muncul dari lemparan dua dadu bersamaan. Probabilitas mendapatkan nilai $x$ paling besar 3 adalah …
A. $\frac{1}{12}$ B. $\frac{1}{9}$ C. $\frac{1}{6}$ D. $\frac{1}{4}$ E. $\frac{1}{3}$
Pembahasan:
Pelemparan dua dadu bersamaan maka $n(S)=6\times 6=36$.
A = kejadian munculnya mata dadu paling besar 3
A = {(1,1), (1,2), (2,1), (1,3), (3,1), (2,2), (2,3), (3,2), (3,3)}
$n(A)=9$
$P(A)=\frac{n(A)}{n(S)}=\frac{9}{36}=\frac{1}{4}$
Jawaban: D
Matematika Dasar SIMAK UI 2016 No. 10
Jika $x+ay=b$, $2x+by=a$, dan $3x+aby=4$, maka $a+b$ = …
A. 0 B. 2 C. 4 D. 6 E. 8
Pembahasan:
$x+ay=b$
$2x+by=a$
------------------- (+)
$3x+(a+b)y=a+b$ …. Pers (4)
$3x+aby=4$ …. Pers (3)
Dari pers (4) dan (3) diperoleh $a+b=4$
Jawaban: C
Matematika Dasar SIMAK UI 2016 No. 11
Banyak susunan huruf berbeda yang dapat dibuat dari semua huruf pada kata SIMAK UI apabila huruf I harus selalu berdekatan adalah …
A. 432 B. 312 C. 240 D. 164 E. 120
Pembahasan:
karena huruf I harus selalu berdekatan, maka dapat anggap “I” adalah “satu” sehingga banyak huruf yang akan disusun adalah 6 (enam), maka diperoleh:
= 6 x 5 x 4 x 3 x 2 x 1 = 720 susunan.
Jawaban: (Tidak ada Opsi)
Matematika Dasar SIMAK UI 2016 No. 12
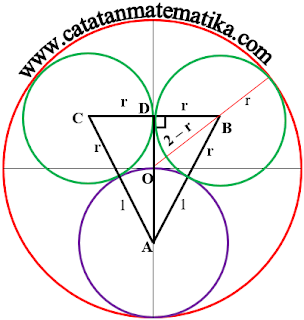
Lingkaran A, B, dan C saling bersinggungan satu sama lain menyinggung lingkaran D pada bagian dalam. Lingkaran B dan C berukuran sama dan lingkaran A memiliki jari-jari 1 serta melalui pusat lingkaran D. Jumlah luas lingkaran A, B, dan C adalah …
A. $\frac{64}{81}\pi $
B. $\frac{112}{81}\pi $
C. $\frac{189}{81}\pi $
D. $\frac{209}{81}\pi $
E. $\frac{225}{81}\pi $
Pembahasan:
Perhatikan gambar berikut!

Misalkan panjang OD = $x$
pada segitiga ADB berlaku pythagoras:
$A{{B}^{2}}=A{{D}^{2}}+B{{D}^{2}}$
${{(r+1)}^{2}}={{(x+1)}^{2}}+{{r}^{2}}$
${{r}^{2}}+2r+1={{x}^{2}}+2x+1+{{r}^{2}}$
$2r={{x}^{2}}+2x$ … pers (1)
Pada segitiga ODB berlaku pythagoras:
$O{{B}^{2}}=O{{D}^{2}}+B{{D}^{2}}$
${{(2-r)}^{2}}={{x}^{2}}+{{r}^{2}}$
$4-4r+{{r}^{2}}={{x}^{2}}+{{r}^{2}}$
$4-4r={{x}^{2}}$
$4-2.2r={{x}^{2}}$; ingat $2r={{x}^{2}}+2x$ maka:
$4-2({{x}^{2}}+2x)={{x}^{2}}$
$3{{x}^{2}}+4x-4=0$
$(3x-2)(x+2)=0$, $x > 0$ maka:
$x=\frac{2}{3}$ substitusi ke:
$4-4r={{x}^{2}}$
$4-4r={{\left( \frac{2}{3} \right)}^{2}}$
$-4r=\frac{4}{9}-4$
$-4r=\frac{-32}{9}\Leftrightarrow r=\frac{8}{9}$
L = 2 x luas lingkaran (r = $\frac{8}{9}$) + luas lingkaran (r = 1).
$L=2\pi {{\left( \frac{8}{9} \right)}^{2}}+\pi {{.1}^{2}}$
$L=\frac{128}{81}\pi +\pi $
$L=\frac{209}{81}\pi $
Jawaban: D
Gunakan petunjuk C dalam menjawab soal nomor 13 sampai nomor 15.
Matematika Dasar SIMAK UI 2016 No. 13
Diketahui $f(x)={{x}^{2}}+3$ dan $g(x)=\sqrt{x-3}$. Pernyataan berikut yang BENAR adalah …
(1) $g$ merupakan invers dari $f$
(2) daerah hasil dari $f\circ g$ adalah himpunan bilangan real.
(3) daerah asal dari $f$ sama dengan daerah hasil dari $g$.
(4) daerah asal dari $g\circ f$ sama dengan daerah asal dari $f$.
Pembahasan:
Pernyataan (1):
$f(x)={{x}^{2}}+3$
${{x}^{2}}+3=y$
${{x}^{2}}=y-3$
$x=\sqrt{y-3}$
${{f}^{-1}}(x)=\sqrt{x-3}=g(x)$. Pernyataan (1) benar.
Pernyataan (2):
$f\circ g={{\left( \sqrt{x-3} \right)}^{2}}+3=x$ maka daerah hasilnya adalah himpunan bilangan real. Pernyataan (2) benar.
Pernyataan (3):
$Df=\{x|x\in R\}$ dan $Rg=\{x|x\in R\}$. Pernyataan (3) benar.
Pernyataan (4):
$g\circ f=\sqrt{({{x}^{2}}+3)-3}=x$ maka $D(g\circ f)=\{x|x\in R\}$ dan $Df=\{x|x\in R\}$. Pernyataan (4) benar.
Jawaban: E (1, 2, 3, 4 benar)
Matematika Dasar SIMAK UI 2016 No. 14
Jika $f(x)=\left\{ \begin{matrix} 2-{{x}^{2}}, & -3\le x\le 0 \\ {{x}^{2}}+2, & 0\le x\le 3 \\ \end{matrix} \right.$, maka …
(1) $f'(-2)+f'(2)=8$
(2) $f(x)$ simetris terhadap sumbu-y
(3) persamaan garis singgung di titik $P(-2,-2)$ dan $Q(2,6)$ adalah sejajar.
(4) $f(x)={{f}^{-1}}(x)$
Pembahasan:
Pernyataan (1):
Untuk $x=-2$ maka:
$f(x)=2-{{x}^{2}}$
$f'(x)=-2x\Leftrightarrow f'(-2)=4$
Untuk $x=2$ maka:
$f(x)={{x}^{2}}+2$
$f'(x)=2x\Leftrightarrow f'(2)=4$
$f'(-2)+f'(2)=4+4=8$. Pernyataan (1) benar.
Pernyataan (2):
$f(x)=a{{x}^{2}}+bx+c$ simetri terhadap sumbu-Y jika $b=0$.
$f(x)=2-{{x}^{2}}$ dan $f(x)={{x}^{2}}+2$ memiliki $b=0$ maka $f(x)$ simetri terhadap sumbu-Y. Pernyataan (2) benar.
Pernyataan (3):
Persamaan garis singgung di titik $P(-2,-2)$ adalah:
$y+2=f'(-2).(x+2)$
$y+2=4(x+2)$
$y=4x+6\Rightarrow {{m}_{1}}=4$
Persamaan garis singgung di titik $Q(2,6)$ adalah:
$y-6=f'(2).(x-2)$
$y-6=4(x-2)$
$y=4x-2\Rightarrow {{m}_{2}}=4$
${{m}_{1}}={{m}_{2}}=4$ maka kedua garis singgung sejajar. Pernyataan (3) benar.
Pernyataan (4):
$f(x)=2-{{x}^{2}}\Leftrightarrow {{f}^{-1}}(x)=\sqrt{2-x}$
$f(x)={{x}^{2}}+2\Leftrightarrow {{f}^{-1}}(x)=\sqrt{x-2}$
Maka $f(x)\ne {{f}^{-1}}(x)$. Pernyataan (4) salah.
Jawaban: A (1, 2, dan 3 benar).
Matematika Dasar SIMAK UI 2016 No. 15

Jika data pada tabel menunjukkan nilai rata-rata ujian siswa di sekolah A dan B, maka …
(1) siswa laki-laki di sekolah A lebih banyak daripada siswa perempuan di sekolah tersebut.
(2) siswa laki-laki di sekolah B lebih banyak daripada siswa perempuan di sekolah tersebut.
(3) siswa laki-laki di sekolah A lebih banyak daripada siswa laki-laki di sekolah B.
(4) nilai rata-rata ujian siswa perempuan di sekolah A dan B adalah 84.
Pembahasan:
Pernyataan (1):
Sekolah A, misalkan:
${{n}_{1}}$ = banyak siswa laki-laki di sekolah A
${{n}_{2}}$ = banyak siswa perempuan di sekolah A
${{\bar{x}}_{1}}=71$, ${{\bar{x}}_{2}}=76$, ${{\bar{x}}_{1,2}}=74$
${{\bar{x}}_{1,2}}=\frac{{{n}_{1}}.{{{\bar{x}}}_{1}}+{{n}_{2}}.{{{\bar{x}}}_{2}}}{{{n}_{1}}+{{n}_{2}}}$
$74=\frac{71{{n}_{1}}+76{{n}_{2}}}{{{n}_{1}}+{{n}_{2}}}$
$74{{n}_{1}}+74{{n}_{2}}=71{{n}_{1}}+76{{n}_{2}}$
$3{{n}_{1}}=2{{n}_{2}}\Leftrightarrow \frac{{{n}_{1}}}{{{n}_{2}}}=\frac{2}{3}$
Artinya, siswa laki-laki di sekolah A lebih sedikit daripada siswa perempuan di sekolah tersebut. Pernyataan 1 salah.
Pernyataan (2):
Sekolah B, misalkan:
${{n}_{3}}$ = banyak siswa laki-laki di sekolah B
${{n}_{4}}$ = banyak siswa perempuan di sekolah B
${{\bar{x}}_{3}}=81$, ${{\bar{x}}_{4}}=90$, ${{\bar{x}}_{3,4}}=84$
${{\bar{x}}_{3,4}}=\frac{{{n}_{3}}.{{{\bar{x}}}_{3}}+{{n}_{4}}.{{{\bar{x}}}_{4}}}{{{n}_{3}}+{{n}_{4}}}$
$84=\frac{81{{n}_{3}}+90{{n}_{4}}}{{{n}_{3}}+{{n}_{4}}}$
$84{{n}_{3}}+84{{n}_{4}}=81{{n}_{3}}+90{{n}_{4}}$
$3{{n}_{3}}=6{{n}_{4}}\Leftrightarrow \frac{{{n}_{3}}}{{{n}_{4}}}=\frac{2}{1}$
Artinya, siswa laki-laki di sekolah B lebih banyak daripada siswa perempuan di sekolah tersebut. Pernyataan 2 benar.
Pernyataan (3):
Siswa laki-laki di sekolah A dan B
${{\bar{x}}_{1}}=71$, ${{\bar{x}}_{3}}=81$, ${{\bar{x}}_{1,3}}=79$
${{\bar{x}}_{1,3}}=\frac{{{n}_{1}}.{{{\bar{x}}}_{1}}+{{n}_{3}}.{{{\bar{x}}}_{3}}}{{{n}_{1}}+{{n}_{3}}}$
$79=\frac{71{{n}_{1}}+81{{n}_{3}}}{{{n}_{1}}+{{n}_{3}}}$
$79{{n}_{1}}+79{{n}_{3}}=71{{n}_{1}}+81{{n}_{3}}$
$8{{n}_{1}}=2{{n}_{3}}\Leftrightarrow \frac{{{n}_{1}}}{{{n}_{3}}}=\frac{1}{4}$
Artinya, siswa laki-laki di sekolah A lebih sedikit daripada siswa laki-laki di sekolah B. Pernyataan (3) salah.
Pernyataan (4):
Siswa perempuan di sekolah A dan B
Ingat:
$\frac{{{n}_{1}}}{{{n}_{2}}}=\frac{2}{3}\Leftrightarrow {{n}_{2}}=\frac{3{{n}_{1}}}{2}$
$\frac{{{n}_{3}}}{{{n}_{4}}}=\frac{2}{1}\Leftrightarrow {{n}_{4}}=\frac{{{n}_{3}}}{2}$
$\frac{{{n}_{1}}}{{{n}_{3}}}=\frac{1}{4}\Leftrightarrow {{n}_{3}}=4{{n}_{1}}$
${{\bar{x}}_{2}}=76$, ${{\bar{x}}_{4}}=90$, ${{\bar{x}}_{2,4}}=x$
${{\bar{x}}_{2,4}}=\frac{{{n}_{2}}.{{{\bar{x}}}_{2}}+{{n}_{4}}.{{{\bar{x}}}_{4}}}{{{n}_{2}}+{{n}_{4}}}$
$x=\frac{\frac{3{{n}_{1}}}{2}.76+\frac{{{n}_{3}}}{2}.90}{\frac{3{{n}_{1}}}{2}+\frac{{{n}_{3}}}{2}}$
$x=\frac{114{{n}_{1}}+45{{n}_{3}}}{\frac{3{{n}_{1}}+{{n}_{3}}}{2}}$
$x=\frac{2(114{{n}_{1}}+45{{n}_{3}})}{3{{n}_{1}}+{{n}_{3}}}$
$x=\frac{2(114{{n}_{1}}+45.4{{n}_{1}})}{3{{n}_{1}}+4{{n}_{1}}}$
$x=\frac{588{{n}_{1}}}{7{{n}_{1}}}=84$
Jadi, nilai rata-rata ujian siswa perempuan di sekolah A dan B adalah 84. Pernyataan (4) benar.
Jawaban: C (2 dan 4 benar)
Baca juga:
|

Post a Comment for "Pembahasan Soal SIMAK UI 2016 Matematika Dasar"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.