Pembahasan Soal SIMAK UI 2011 Matematika IPA Kode 511
Matematika IPA SIMAK UI 2011 No. 1
Misalkan A adalah suatu matriks $2\times 2$. Jika ${{A}^{2}}-5A+7I=0$ maka jumlah elemen-elemen diagonal utama dari matriks A adalah …A. 2 B. 3 C. 4 D. 5 E. 6
Pembahasan:
Misalkan $A=\left( \begin{matrix} a & b \\ c & d \\ \end{matrix} \right)$ maka:
${{A}^{2}}=\left( \begin{matrix} a & b \\ c & d \\ \end{matrix} \right)\left( \begin{matrix} a & b \\ c & d \\ \end{matrix} \right)$
${{A}^{2}}=\left( \begin{matrix} {{a}^{2}}+bc & ad+bd \\ ac+cd & bc+{{d}^{2}} \\ \end{matrix} \right)$
${{A}^{2}}-5A+7I=0$
$\left( \begin{matrix} {{a}^{2}}+bc & ab+bd \\ ac+cd & bc+{{d}^{2}} \\ \end{matrix} \right)-5\left( \begin{matrix} a & b \\ c & d \\ \end{matrix} \right)+7\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right)=0$
$\left( \begin{matrix} {{a}^{2}}+bc & ab+bd \\ ac+cd & bc+{{d}^{2}} \\ \end{matrix} \right)-\left( \begin{matrix} 5a & 5b \\ 5c & 5d \\ \end{matrix} \right)+\left( \begin{matrix} 7 & 0 \\ 0 & 7 \\ \end{matrix} \right)=0$
$\left( \begin{matrix} {{a}^{2}}+bc-5a+7 & ab+bd-5b \\ ac+cd-5c & bc+{{d}^{2}}-5d+7 \\ \end{matrix} \right)=0$
$\left( \begin{matrix} {{a}^{2}}+bc-5a+7 & b(a+d-5) \\ c(a+d-5) & bc+{{d}^{2}}-5d+7 \\ \end{matrix} \right)=0$
$\begin{align} b(a+d-5) &= 0 \\ a+d-5 &= 0 \\ a+d &= 5 \end{align}$
Jadi, jumlah diagonal utama adalah: $a+d=5$
Jawaban: D
Matematika IPA SIMAK UI 2011 No. 2
Jika sistem persamaan $\left\{ \begin{align} ax+2y &=b+1 \\ x+y &= 3 \end{align} \right.$ dan $\left\{ \begin{align} 2x+y &= {{a}^{2}}+2 \\ x+3y &= 3 \end{align} \right.$
Mempunyai solusi yang sama, maka banyaknya pasangan bilangan $(a,b)$ adalah …
A. 0
B. 1
C. 2
D. 3
E. tak berhingga
Pembahasan:
$ax+2y=b+1$ … (1)
$x+y=3$ … (2)
$2x+y={{a}^{2}}+2$ … (3)
$x+3y=3$ … (4)
Pers (2) dikurang (4) maka:
$x+y=3$
$x+3y=3$
------------ (-)
$-2y=0\Leftrightarrow y=0,x=3$
Nilai $x=3,\,y=0$ substitusi ke persamaan (3) diperoleh:
$\begin{align} 2.3+0 &= {{a}^{2}}+2 \\ {{a}^{2}}-4 &= 0 \\ (a+2)(a-2) &= 0 \end{align}$
$a=-2$ atau $a=2$
Substitusi ke (1):
$ax+2y=b+1$
$a.3+2.0-1=b$
$b=3a-1$
$a=-2\to b=3(-2)-1\Leftrightarrow b=-7$
$a=2\to b=3.2-1\Leftrightarrow b=5$
Nilai $(a,b)$adalah$(-2,-7)$ atau $(2,5)$maka ada 2 pasang.
Jawaban: C
Matematika IPA SIMAK UI 2011 No. 3
Misalkan $f(x)$ adalah suatu polinomial derajat tiga yang akar-akarnya membentuk barisan aritmetika dengan nilai suku ketiga adalah tiga kali nilai suku pertama; dan jumlah akar-akarnya sama dengan 12, maka sisa dari pembagian $f(x+6)$ oleh ${{x}^{2}}+1$ adalah …A. $7x-6$
B. $x+6$
C. $6x-7$
D. $x-6$
E. $x+1$
Pembahasan:
Misalkan $f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ akar-akarnya ${{x}_{1}}$, ${{x}_{2}}$, dan ${{x}_{3}}$.
Barisan Aritmetika:
${{x}_{1}}$, ${{x}_{2}}$, dan ${{x}_{3}}$
$2{{x}_{2}}={{x}_{1}}+{{x}_{3}}$ … (1)
${{x}_{3}}=3{{x}_{1}}$ … (2)
Jumlah akar-akar:
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}=12$ … (3)
Dari (1) dan (3)
$\begin{align} {{x}_{1}}+{{x}_{2}}+{{x}_{3}} &= 12 \\ ({{x}_{1}}+{{x}_{3}})+{{x}_{2}} &= 12 \\ 2{{x}_{2}}+{{x}_{2}} &= 12 \\ 3{{x}_{2}} &= 12 \\ {{x}_{2}} &= 4 \end{align}$
Substitusi ${{x}_{2}}=4$ dan ${{x}_{3}}=3{{x}_{1}}$ ke (1) diperoleh:
$2.4={{x}_{1}}+3{{x}_{1}}\Leftrightarrow {{x}_{1}}=2$
${{x}_{3}}=3{{x}_{1}}\Leftrightarrow {{x}_{3}}=3.2=6$
$\begin{align} f(x) &= (x-{{x}_{1}})(x-{{x}_{2}})(x-{{x}_{3}}) \\ f(x) &= (x-2)(x-4)(x-6) \\ f(x+6) &= (x+6-2)(x+6-4)(x+6-6) \\ &=(x+4)(x+2)x \\ f(x+6) &= {{x}^{3}}+6{{x}^{2}}+8x \end{align}$
Sisa $f(x+6):({{x}^{2}}+1)$
Substitusi ${{x}^{2}}=-1$ ke:
$f(x+6)={{x}^{3}}+6{{x}^{2}}+8x$
$\begin{align} sisa &= {{x}^{2}}.x+6{{x}^{2}}+8x \\ &= -x+6(-1)+8x \\ &= 7x-6 \end{align}$
Jawaban: A
Matematika IPA SIMAK UI 2011 No. 4
Nilai-nilai $x$, untuk ${{0}^{o}}\le x\le {{360}^{o}}$ yang memenuhi $\sin x+\sin 2x > \sin 3x$ adalah …A. ${{0}^{o}} < x < {{120}^{o}}$, ${{180}^{o}} < x < {{240}^{o}}$
B. ${{0}^{o}} < x < {{150}^{o}}$, ${{180}^{o}} < x < {{270}^{o}}$
C. ${{120}^{o}} < x < {{180}^{o}}$, ${{240}^{o}} < x < {{360}^{o}}$
D. ${{150}^{o}} < x < {{180}^{o}}$, ${{270}^{o}} < x < {{360}^{o}}$
E. ${{0}^{o}} < x < {{135}^{o}}$, ${{180}^{o}} < x < {{270}^{o}}$
Pembahasan:
$\sin x+\sin 2x > \sin 3x$
$\sin 2x > \sin 3x-\sin x$
$2\sin x.\cos x > 2.\cos \left( \frac{3x+x}{2} \right).\sin \left( \frac{3x-x}{2} \right)$
$2\sin x.\cos x > 2\cos 2x.\sin x$
$\sin x.\cos x > (2{{\cos }^{2}}x-1)\sin x$
$\sin x(\cos x-2{{\cos }^{2}}x+1) > 0$
$\sin x(2{{\cos }^{2}}x-\cos x-1) < 0$
$\sin x(2\cos x+1)(\cos x-1) < 0$ $x$
pembuat nol:
$\begin{align} \sin x &= 0 \\ x &= {{0}^{o}} \\ x &= {{180}^{o}} \end{align}$
$\begin{align} 2\cos x+1 &= 0 \\ \cos x &= -\frac{1}{2} \\ x &= {{120}^{o}} \\ x &= {{240}^{o}} \end{align}$
$\begin{align} \cos x-1 &= 0 \\ \cos x &= 1 \\ x &= {{0}^{o}} \\ x &= {{360}^{o}} \end{align}$
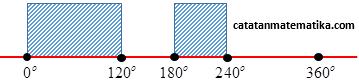
${{0}^{o}} < x < {{120}^{o}}$, ${{180}^{o}} < x < {{240}^{o}}$
Jawaban: A
Matematika IPA SIMAK UI 2011 No. 5
Pada suatu barisan geometri dengan $r>1$, diketahui dua kali jumlah empat suku pertama adalah tiga kali jumlah dua suku genap pertama. Jika di antara suku-suku tersebut disisipkan empat bilangan, dengan cara: antara suku kedua dan suku ketiga disisipkan satu bilangan, dan antara suku ketiga dan keempat disisipkan tiga bilangan maka akan terbentuk barisan aritmetika dengan beda $r$. Jumlah bilangan yang disisipkan adalah …A. 14
B. 24
C. 28
D. 32
E. 42
Pembahasan:
Deret geometri dengan $r>1$
$\begin{align} 2{{S}_{4}} &= 3({{U}_{2}}+{{U}_{4}}) \\ 2\left( \frac{a({{r}^{4}}-1)}{r-1} \right) &= 3(ar+a{{r}^{3}}) \\ \frac{2a({{r}^{2}}+1)(r+1)(r-1)}{(r-1)} &= 3ar({{r}^{2}}+1) \\ 2r+2 &= 3r \\ r &= 2 \end{align}$
Barisan Geometri:
$a$, $2a$, $4a$, $8a$
Barisan Aritmetika: $b=r=2$
$a$, $2a$, …, $4a$, …, …., …., $8a$
$a$, $2a$, ${{U}_{3}}$, $4a$, ${{U}_{5}}$, ${{U}_{6}}$, ${{U}_{7}}$, $8a$
$\begin{align} b &= 2a-a \\ b &= a \\ 2 &= a \end{align}$
Jumlah bilangan yang disisipkan:
= ${{U}_{3}}+{{U}_{5}}+{{U}_{6}}+{{U}_{7}}$
= $(a+2b)+(a+4b)+(a+5b)+(a+6b)$
= $4a+17b$
= $4.2+17.2$
= 42
Jawaban: E
Matematika IPA SIMAK UI 2011 No. 6
Jika $\sin x-\sin y=-\frac{1}{3}$ dan $\cos x-\cos y=\frac{1}{2}$, maka nilai dari $\sin (x+y)$ = ….A. $\frac{12}{13}$
B. $\frac{12}{15}$
C. $\frac{12}{17}$
D. $\frac{12}{19}$
E. $\frac{12}{21}$
Pembahasan:
$\sin x-\sin y=-\frac{1}{3}$
$2\cos \frac{1}{2}(x+y).\sin \frac{1}{2}(x-y)=-\frac{1}{3}$ … (1)
$\cos x-\cos y=\frac{1}{2}$
$-2\sin \frac{1}{2}(x+y).\sin \frac{1}{2}(x-y)=\frac{1}{2}$ … (2)
Persamaan (2) dibagi persamaan (1):
$\frac{-2\sin \frac{1}{2}(x+y).\sin \frac{1}{2}(x-y)}{2\cos \frac{1}{2}(x+y).\sin \frac{1}{2}(x-y)}=\frac{\frac{1}{2}}{-\frac{1}{3}}$
$-\tan \frac{1}{2}(x+y)=\frac{-3}{2}$
$\tan \frac{1}{2}(x+y)=\frac{3}{2}=\frac{de}{sa}$
$\begin{align} mi &= \sqrt{d{{e}^{2}}+s{{a}^{2}}} \\ &= \sqrt{{{3}^{2}}+{{2}^{2}}} \\ mi &= \sqrt{13} \end{align}$
$\sin \frac{1}{2}(x+y)=\frac{de}{mi}=\frac{3}{\sqrt{13}}$
$\cos \frac{1}{2}(x+y)=\frac{sa}{mi}=\frac{2}{\sqrt{13}}$
$\begin{align} \sin (x+y) &= 2.\sin \frac{1}{2}(x+y).\cos \frac{1}{2}(x+y) \\ &= 2.\frac{3}{\sqrt{13}}.\frac{2}{\sqrt{13}} \\ &= \frac{12}{13} \end{align}$
Jawaban: A
Matematika IPA SIMAK UI 2011 No. 7
Sebuah kerucut tegak tanpa alas diletakkan terbalik. Sebuah bola berdiameter 16 cm dimasukkan ke dalam kerucut sehingga semua bagian bola masuk ke dalam kerucut. Kerucut dengan volume terkecil yang mungkin mempunyai ukuran tinggi …A. $8\sqrt{2}$ cm
B. $8\sqrt{3}$ cm
C. $16\sqrt{2}$ cm
D. 24 cm
E. 32 cm
Pembahasan:
Perhatikan sketsa gambar berikut:
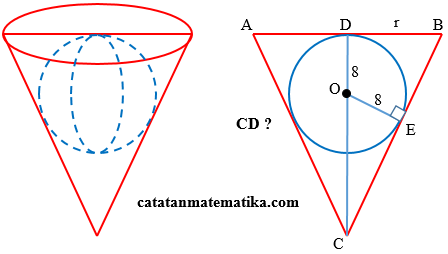
Perhatikan segitiga BDC:
CD = t, BD = r, maka BC = $\sqrt{{{r}^{2}}+{{t}^{2}}}$
Perhatikan segitiga CEO:
OC = $t-8$, OE = 8
Segitiga BDC sebangun dengan segitiga CEO, maka:
$\begin{align} \frac{BD}{OE} &= \frac{BC}{OC} \\ \frac{r}{8} &= \frac{\sqrt{{{r}^{2}}+{{t}^{2}}}}{t-8} \\ 8\sqrt{{{r}^{2}}+{{t}^{2}}} &= r(t-8) \\ 64({{r}^{2}}+{{t}^{2}}) &= {{r}^{2}}{{(t-8)}^{2}} \\ {{r}^{2}}[(64-{{(t-8)}^{2}}] &= -64{{t}^{2}} \\ {{r}^{2}}(-{{t}^{2}}+16t) &= -64{{t}^{2}} \\ {{r}^{2}} &= \frac{-64{{t}^{2}}}{-{{t}^{2}}+16t} \\ {{r}^{2}} &= \frac{64t}{t-16} \end{align}$
Volume kerucut:
$\begin{align} V &= \frac{1}{3}\pi {{r}^{2}}t \\ & = \frac{1}{3}\pi .\frac{64t}{t-16}.t \\ V &= \frac{64\pi }{3}.\frac{{{t}^{2}}}{t-16} \end{align}$
$\begin{align} \frac{dV}{dt} &= 0 \\ \frac{64\pi }{3}\left( \frac{2t(t-16)-{{t}^{2}}}{{{(t-6)}^{2}}} \right) &= 0 \\ 2{{t}^{2}}-32t-{{t}^{2}} &= 0 \\ {{t}^{2}}-32t &= 0 \\ t(t-32) &= 0 \\ t &= 32 \end{align}$
Jawaban: E
Matematika IPA SIMAK UI 2011 No. 8
Misalkan salah satu akar dari persamaan $(k-5){{x}^{2}}-2kx+k-4=0$ bernilai lebih dari 2 dan salah satu akar yang lain bernilai kurang dari 1, maka himpunan semua bilangan $k$ yang memenuhi adalah …A. $\{k\in R|5 < k < 24 \}$
B. $\{k\in R|5 < k < 20 \}$
C. $\{k\in R|15 < k < 24 \}$
D. $\{k\in R|k > 5 \}$
E. $\{k\in R|k > 24 \}$
Pembahasan:
$(k-5){{x}^{2}}-2kx+k-4=0$
$\begin{align} {{x}_{1}} &> 2 \\ {{x}_{1}}-2 &> 0 \end{align}$ dan $\begin{align} {{x}_{2}} &< 1 \\ {{x}_{2}}-1 &< 0 \end{align}$
$\begin{align} ({{x}_{1}}-2)({{x}_{2}}-1) &< 0 \\ {{x}_{1}}.{{x}_{2}}-{{x}_{1}}-2{{x}_{2}}+2 &< 0 \end{align}$
Ada 2 kemungkinan:
Kemungkinan I:
${{x}_{1}}.{{x}_{2}}-{{x}_{1}}-2{{x}_{2}}+2 < 0$
${{x}_{1}}{{x}_{2}}-({{x}_{1}}+{{x}_{2}})-{{x}_{2}}+2 < 0$
$\frac{(k-4)}{(k-5)}-\frac{2k}{k-5}+2<{{x}_{2}} < 1$
$\frac{-k-4}{k-5}+1 < 0$
$\frac{-k-4+k-5}{k-5} < 0$
$\frac{-9}{k-5} < 0$
$k > 5$
Kemungkinan II:
${{x}_{1}}{{x}_{2}}-{{x}_{1}}-2{{x}_{2}}+2 < 0$ ${{x}_{1}}{{x}_{2}}-2({{x}_{1}}+{{x}_{2}})+{{x}_{1}}+2 < 0$
$\frac{k-4}{k-5}-2.\frac{2k}{k-5}+{{x}_{1}}+\frac{2(k-5)}{k-5} < 0$
$\frac{k-4}{k-5}-\frac{4k}{k-5}+{{x}_{1}}+\frac{2k-10}{k-5} < 0$
$\frac{-k-14}{k-5}+{{x}_{1}} < 0$ ${{x}_{1}} < \frac{k+14}{k-5}$,
ingat ${{x}_{1}} > 2\Leftrightarrow 2 < {{x}_{1}}$
$2 < {{x}_{1}} < \frac{k+14}{k-5}$
$2 < \frac{k+14}{k-5}$
$\frac{2(k-5)}{k-5}-\frac{k+14}{k-5} < 0$
$\frac{k-24}{k-5} < 0$, karena $k-5 > 0$ maka $k-24 < 0\Leftrightarrow k < 24$
Dari I dan II diperoleh: $\{k\in R|5 < k < 24 \}$
Jawaban: A
Matematika IPA SIMAK UI 2011 No. 9
Misalkan fungsi $f:R\to R$ dan $g:R\to R$ didefinisikan dengan $f(x)=1+\frac{1}{x}$ dan $g(x)=1-\frac{1}{x}$. Batas nilai $x$ dimana berlaku $(f\circ g)(x) < (g\circ f)(x)$ adalah …A. $-1 < x < 1$
B. $-1 < x < 0$
C. $0 < x < 1$
D. $x < -1$ atau $x > 1$
E. $-1 < x < 0$ atau $0 < x < 1$
Pembahasan:
$f(x)=1+\frac{1}{x}\Leftrightarrow f(x)=\frac{x+1}{x}$
$g(x)=1-\frac{1}{x}=\frac{x-1}{x}$
$(f\circ g)(x) < (g\circ f)(x)$
$f(g(x)) < g(f(x))$
$f\left( \frac{x-1}{x} \right) < g\left( \frac{x+1}{x} \right)$
$\frac{\frac{x-1}{x}+1}{\frac{x-1}{x}} < \frac{\frac{x+1}{x}-1}{\frac{x+1}{x}}$
$\frac{\frac{2x-1}{x}}{\frac{x-1}{x}} < \frac{\frac{1}{x}}{\frac{x+1}{x}}$
$\frac{2x-1}{x-1} < \frac{1}{x+1}$ $\frac{2x-1}{x-1}-\frac{1}{x+1} < 0$
$\frac{(2x-1)(x+1)-(x-1)}{(x-1)(x+1)} < 0$ $\frac{2{{x}^{2}}+2x-x-1-x+1)}{(x-1)(x+1)} < 0$
$\frac{2{{x}^{2}}}{(x-1)(x+1)} < 0$,
karena $2{{x}^{2}} > 0$ atau $x \ne 0$ maka:
$(x-1)(x+1) < 0$ $-1 < x < 1$ , $x\ne 0$
HP = {$-1 < x < 1$ atau $-1 < x < 1$}
Jawaban: E
Matematika IPA SIMAK UI 2011 No. 10
Jika daerah yang dibatasi oleh sumbu Y, kurva $y={{x}^{2}}$ dan garis $y={{a}^{2}}$ dimana $a \ne 0$ diputar mengelilingi sumbu X volumenya sama dengan jika daerah itu diputar mengelilingi sumbu Y. Nilai $a$ yang memenuhi adalah …A. $\frac{5}{8}$
B. $\frac{3}{8}$
C. $\frac{2}{5}$
D. $\frac{8}{5}$
E. $\frac{5}{2}$
Pembahasan:
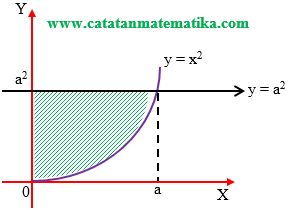
Volume diputar sumbu X = Volume diputar sumbu Y
$\begin{align} \pi \int\limits_{0}^{a}{({{a}^{4}}-{{x}^{4}})dx} &= \pi \int\limits_{0}^{{{a}^{2}}}{ydy} \\ \int\limits_{0}^{a}{({{a}^{4}}-{{x}^{4}})dx} &= \int\limits_{0}^{{{a}^{2}}}{ydy} \\ {{a}^{4}}x-\frac{1}{5}{{x}^{5}} &= \frac{1}{2}{{y}^{2}} \\ {{a}^{4}}.a-\frac{4}{5}.{{a}^{5}} &= \frac{1}{2}{{({{a}^{2}})}^{2}} \\ {{a}^{5}}-\frac{1}{5}{{a}^{5}} &= \frac{1}{2}{{a}^{4}} \\ \frac{4}{5}{{a}^{5}} &= \frac{1}{2}{{a}^{4}} \\ \frac{4}{5}a &= \frac{1}{2} \\ a &= \frac{5}{8} \end{align}$
Jawaban: A
Matematika IPA SIMAK UI 2011 No. 11
Diberikan kubus ABCD.EFGH dengan panjang rusuk 2 cm. Titik P terletak pada rusuk FG sehingga FP = 2PG. Jika $\alpha $ adalah bidang irisan kubus yang melalui titik B, D, dan P, maka luas bidang $\alpha $ adalah … $c{{m}^{2}}$.A. $\frac{8}{9}\sqrt{22}$
B. $\frac{6}{9}\sqrt{22}$
C. $\frac{5}{9}\sqrt{22}$
D. $\frac{3}{9}\sqrt{22}$
E. $\frac{1}{9}\sqrt{22}$
Pembahasan:
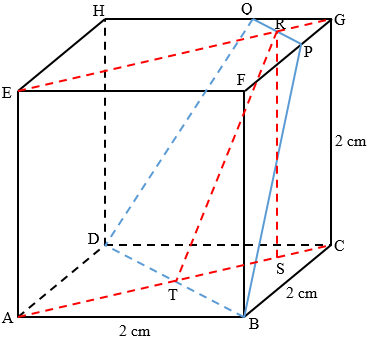
Luas bidang $\alpha $ = Luas BPQD = …?
$\begin{align} TC &=\frac{1}{2}AC \\ & =\frac{1}{2}.2\sqrt{2} \\ TC &=\sqrt{2} \end{align}$
$TS=\frac{2}{3}TC=\frac{2}{3}\sqrt{2}$
RS = 2
$\begin{align}
TR &= \sqrt{T{{S}^{2}}+R{{S}^{2}}} \\ &= \sqrt{{{\left( \frac{2}{3}\sqrt{2} \right)}^{2}}+{{2}^{2}}} \\ &= \sqrt{\frac{8}{9}+\frac{36}{9}} \\ &= \sqrt{\frac{44}{9}} \\ TR &= \frac{2}{3}\sqrt{11} \end{align}$
Perhatikan segitiga PGQ:
GP = GQ = $\frac{2}{3}$ maka $PQ=\frac{2}{3}\sqrt{2}$
Bidang $\alpha $ berbentuk trapesium, dengan BD = $2\sqrt{2}$ maka:
$\begin{align} L &= \frac{1}{2}\left( BD+PQ \right).TR \\ & = \frac{1}{2}\left( 2\sqrt{2}+\frac{2}{3}\sqrt{2} \right).\frac{2}{3}\sqrt{11} \\ & = \frac{1}{2}.\frac{8}{3}\sqrt{2}.\frac{2}{3}\sqrt{11} \\ L &= \frac{8}{9}\sqrt{22} \end{align}$
Jawaban: A
Matematika IPA SIMAK UI 2011 No. 12
$\underset{a\to b}{\mathop{\lim }}\,\frac{\tan a-\tan b}{1+\left( 1-\frac{a}{b} \right)\tan a.\tan b-\frac{a}{b}}$ = …A. $\frac{1}{b}$
B. b
C. –b
D. $\frac{-1}{b}$
E. 1
Pembahasan:
$\underset{a\to b}{\mathop{\lim }}\,\frac{\tan a-\tan b}{1+\left( 1-\frac{a}{b} \right)\tan a.\tan b-\frac{a}{b}}$
= $\underset{a \rightarrow b}{\mathop{\lim }}\,\frac{\tan a-\tan b}{\left( 1-\frac{a}{b} \right)+\left( 1-\frac{a}{b} \right)\tan a.\tan b}$
= $\underset{a \rightarrow b}{\mathop{\lim }}\,\frac{\tan a-\tan b}{\left( 1-\frac{a}{b} \right)\left( 1+\tan a.\tan b \right)}$
= $\underset{a \rightarrow b}{\mathop{\lim }}\,\frac{\tan (a-b)}{\left( \frac{b-a}{b} \right)}$
= $\underset{a \rightarrow b}{\mathop{\lim }}\,\frac{-b.\tan (a-b)}{(a-b)}$
= $-b$
Jawaban: C
Artikel Terkait:
|
Semoga postingan: Pembahasan Soal SIMAK UI 2011 Matematika IPA Kode 511 ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.
Post a Comment for "Pembahasan Soal SIMAK UI 2011 Matematika IPA Kode 511"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.