Dimensi Tiga 2. Jarak Titik ke Garis pada Bangun Ruang

A. Definisi Jarak Titik ke Garis

Jarak titik A ke garis g adalah ruas garis terpendek yang menghubungkan titik A ke garis g. Ruas garis terpendek tersebut diperoleh dengan menarik garis dari titik A tegak lurus terhadap garis g.

Perhatikan gambar berikut:

B. Contoh Soal dan Pembahasan

Contoh 1. (Latihan 1.2 Matematika Wajib Kelas 12)

Diketahui limas beraturan T.ABCD, panjang rusuk AB = 3 cm dan TA = 6 cm. Tentukan jarak titik B dan rusuk TD.
Pembahasan:
Lukis garis dari titik B yang tegak lurus dengan DT (perhatikan gambar).
Dari gambar diperoleh bahwa jarak titik B ke garis DT adalah panjang ruas garis BE. Untuk itu perhatikan segitiga BDT.

Kemudian lukis garis tinggi dari titik T ke garis BD (seperti gambar di atas). TB = TD = 6 cm, maka garis tinggi TO membagi dua sama panjang garis BD (OB = OD).
$\begin{align} BD &=\sqrt{AB^2+AD^2} \\ &=\sqrt{3^2+3^2} \\ BD &=3\sqrt{2} \end{align}$
$OB=\frac{1}{2}BD=\frac{3}{2}\sqrt{2}$
Perhatikan segitiga TOB:
$\begin{align} OT &=\sqrt{TB^2-OB^2} \\ & =\sqrt{6^2-\left( \frac{3}{2}\sqrt{2} \right)^2} \\ & =\sqrt{36-\frac{9}{2}} \\ & =\sqrt{\frac{63}{2}} \\ OT &=\frac{3\sqrt{7}}{\sqrt{2}} \end{align}$
Dengan menggunakan luas segitiga TDB maka:
$\begin{align} \frac{1}{2}.TD.BE &=\frac{1}{2}.BD.OT \\ TD.BE &= BD.OT \\ 6.BE &= 3\sqrt{2}.\frac{3\sqrt{7}}{\sqrt{2}} \\ BE &= \frac{9\sqrt{7}}{6} \\ BE &= \frac{3\sqrt{7}}{2} \end{align}$
Jadi, jarak titik B ke garis DT adalah $\frac{3\sqrt{7}}{2}$.

Contoh 2. (Latihan 1.2 Matematika Wajib Kelas 12)

Diketahui limas segi enam beraturan T.ABCDEF dengan panjang rusuk AB = 10 cm dan AT = 13 cm. Tentukan jarak antara titik B dan rusuk TE.
Pembahasan:
Perhatikan gambar berikut!

Jarak titik B ke garis TE adalah panjang ruas garis BP.
Perhatikan segitiga TBE

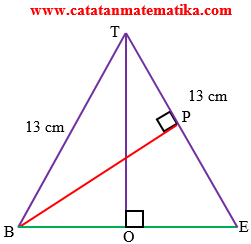
Karena ABCDEF adalah segi-6 beraturan, maka BE = 20 cm.
$OB=\frac{1}{2}BE=10$
TB = TE = AT = 13
Perhatikan segitiga BOT:
$\begin{align} OT &=\sqrt{TB^2-OB^2} \\ &=\sqrt{{13}^2-{10}^2} \\ OT &=\sqrt{69} \end{align}$
Dengan menggunakan luas segitiga TBE, maka:
$\begin{align} \frac{1}{2}.TE.BP &=\frac{1}{2}.OT.BE \\ 13.BP &= \sqrt{69}\times 20 \\ BP &= \frac{20}{13}\sqrt{69} \end{align}$
Jadi, jarak titik B ke garis TE adalah $\frac{20}{13}\sqrt{69}$.

Contoh 3. (Latihan 1.2 Matematika Wajib Kelas 12)

Diketahui kubus ABCD.EFGH dengan rusuk AB = 10 cm. Tentukan:
a. jarak titik F ke garis AC.
b. jarak titik H ke garis DF.
Pembahasan:
a. jarak titik F ke garis AC

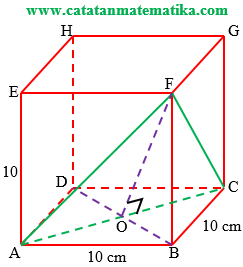
Perhatikan gambar di atas, jarak titik T ke garis AC adalah panjang garis OF.
Perhatikan segitiga AOF:
$AF=10\sqrt{2}$
$\begin{align} OA &=\frac{1}{2}AC \\ & =\frac{1}{2}.10\sqrt{2} \\ OA &= 5\sqrt{2} \end{align}$
$\begin{align} OF &= \sqrt{AF^2-OA^2} \\ &=\sqrt{(10\sqrt{2})^2-(5\sqrt{2})^2} \\ &=\sqrt{200-50} \\ &=\sqrt{150} \\ &=\sqrt{25\times 6} \\ OF &=5\sqrt{6} \end{align}$

b. jarak titik H ke garis DF
perhatikan gambar berikut!

Jarak titik H ke garis DF adalah panjang garis PH.
Perhatikan segitiga DHF:

Menggunakan luas DHF, maka:
$\begin{align} \frac{1}{2}.DF.PH &=\frac{1}{2}.HF.DH \\ 10\sqrt{3}.PH &=10\sqrt{2}.10 \\ PH &=\frac{10\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ PH &=\frac{10}{3}\sqrt{6} \end{align}$
Jadi, jarak titik H ke garis DF adalah $\frac{10}{3}\sqrt{6}$.

Contoh 4. (Latihan 1.2 Matematika Wajib Kelas 12)

Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. Titik M adalah titik tengah BC. Tentukan jarak M ke EG.
Pembahasan:

Jarak titik M ke garis EG adalah panjang garis MN.
Perhatikan segitiga EBM siku-siku di B:
$\begin{align} EM &=\sqrt{BE^2+BM^2} \\ & =\sqrt{(8\sqrt{2})^2+4^2} \\ & =\sqrt{128+16} \\ EM &=12 \end{align}$
Perhatikan segitiga MCG siku-siku di C:
$\begin{align} MG &=\sqrt{CM^2+CG^2} \\ &=\sqrt{4^2+8^2} \\ &=\sqrt{80} \\ MG &= 4\sqrt{5} \end{align}$
Lihat segitiga EGM, berlaku aturan cosinus:
$\begin{align} \cos \angle EGM &= \frac{EG^2+MG^2-EM^2}{2.EG.MG} \\ &=\frac{{{(8\sqrt{2})}^{2}}+(4\sqrt{5})-{{12}^{2}}}{2.8\sqrt{2}.4\sqrt{5}} \\ &=\frac{128+80-144}{64\sqrt{10}} \\ \cos \angle EGM &=\frac{1}{\sqrt{10}} \\ \sin \angle EGM &=\frac{\sqrt{(\sqrt{10})^2-1}}{\sqrt{10}} \\ \sin \angle EGM &=\frac{3}{\sqrt{10}} \end{align}$
Dengan menggunakan luas segitiga EGM, maka:
$\begin{align} \frac{1}{2}.EG.MN &= \frac{1}{2}.EG.MG.\sin \angle EGM \\ MN &= MG.\sin \angle EGM \\ &= 4\sqrt{5}.\frac{3}{\sqrt{10}} \\ &=\frac{12}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ MN &= 6\sqrt{2} \end{align}$
Jadi, jarak titik M ke garis EG adalah $6\sqrt{2}$.

Contoh 5. (Latihan 1.2 Matematika Wajib Kelas 12)

Perhatikan limas segi empat beraturan berikut.

Titik P dan Q berturut-turut adalah titik tengah rusuk AB dan AD. Jika panjang AB = TA = 12 cm, tentukan jarak antara titik T dan garis PQ!
Pembahasan:

Berdasarkan gambar! Jarak titik T ke garis PQ adalah panjang garis TR.
Perhatikan segitiga TAB:

$\begin{align}TP &= \sqrt{AT^2-AP^2} \\ &= \sqrt{12^2-6^2} \\ &= \sqrt{108} \\ TP &= 6\sqrt{3} \end{align}$
Perhatikan segitiga QAP siku-siku di titik A.

$\begin{align}PQ &= \sqrt{AQ^2+AP^2} \\ &= \sqrt{6^2+6^2} \\ PQ &= 6\sqrt{2} \end{align}$
Perhatikan segitiga TQP segitiga sama kaki TQ = TP.

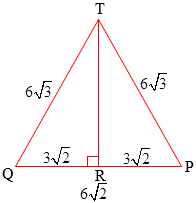
$\begin{align}TR &= \sqrt{TP^2-PR^2} \\ &= \sqrt{(6\sqrt{3})^2-(3\sqrt{2})^2} \\ &= \sqrt{108-18} \\ &= \sqrt{90} \\ TR &= 3\sqrt{10} \end{align}$
Jadi, jarak titik T ke garis PQ adalah $3\sqrt{10}$ cm.

C. Soal Latihan

1. Diketahui kubus ABCD.EFGH, rusuk-rusuknya 20 cm. Jarak titik E ke garis BD adalah … cm.
2. Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik A ke garis DF adalah … cm.
3. Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm. Titik M adalah titik tengah rusuk BC. Jarak titik M ke garis EG adalah … cm.
4. Limas beraturan T.ABCD dengan panjang rusuk alas 12 cm dan panjang rusuk tegak $12\sqrt{2}$ cm. Jarak titik A ke garis TC adalah ... cm.
5. Diketahui balok ABCD.EFGH dengan AB = 24 cm, BC = 8 cm dan CG = 6 cm. Tentukan jarak titik B ke garis AG.

Semoga postingan: Dimensi Tiga 2. Jarak Titik ke Garis pada Bangun Ruang ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Dapatkan Update terbaru, subscribe channel kami:

Share :