Dimensi Tiga 1. Jarak Titik ke Titik pada Bangun Ruang
A. Definisi Jarak Titik ke Titik
Jarak titik A ke titik B adalah penghubung terpendek A dan B yakni ruas garis AB.
B. Contoh Soal dan Pembahasan
Contoh 1. (Latihan 1.1 Matematika Wajib Kelas 12)
Diketahui limas T.ABC dengan bidang alas berbentuk segitiga sama sisi. TA tegak lurus bidang alas. Jika panjang AB = $4\sqrt{2}$ cm dan TA = 4 cm. Jarak titik T ke C!Penyelesaian:
Perhatikan gambar limas T.ABC berikut ini.
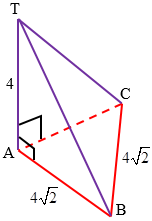
Jarak titik T ke C adalah panjang ruas TC.
Perhatikan segitiga TAC, siku-siku di A.
AC = AB = $4\sqrt{2}$
$\begin{align} TC &= \sqrt{TA^2+AC^2} \\ & =\sqrt{4^2+(4\sqrt{2})^2} \\ & =\sqrt{16+32} \\ &=\sqrt{48} \\ & =\sqrt{16\times 3} \\ TC &=4\sqrt{3} \end{align}$.
Jadi, jarak titik T ke titik C adalah $4\sqrt{3}$ cm.
Contoh 2. (Latihan 1.1 Matematika Wajib Kelas 12)
Perhatikan limas segi enam beraturan berikut.
Diketahui panjang AB = 10 cm dan TA = 13 cm. Titik O merupakan titik tengah garis BE. Tentukan jarak antara titik T dan O!
Penyelesaian:
Perhatikan gambar berikut!
Karena alas segi-6 beraturan dengan rusuk AB = 10 cm, maka OB = AB = 10 cm.
Jarak titik T dan O adalah panjang ruas garis TO.
Perhatikan segitiga TOB:
TB = TA = 13 cm, dengan teorema pythagoras maka:
$\begin{align} TO &= \sqrt{TB^2-OB^2} \\ &= \sqrt{13^2-10^2} \\ TO &=\sqrt{69} \end{align}$
Jadi, jarak titik T ke titik O adalah $\sqrt{69}$
Contoh 3. (Latihan 1.1 Matematika Wajib Kelas 12)
Perhatikan bangun berikut ini.
Jika diketahui panjang AB = 5 cm, AE = BC = EF = 4 cm, maka tentukan:
a. Jarak antara titik A dan C
b. Jarak antara titik E dan C
c. Jarak antara titik A dan G
Penyelesaian:
a. Jarak antara titik A dan C
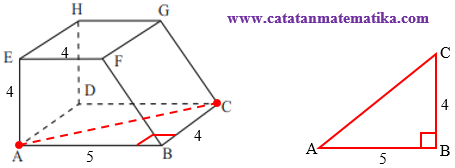
Jarak antara titik A dan C adalah panjang ruas garis AC.
Perhatikan segitiga ABC maka:
$\begin{align} AC &=\sqrt{AB^2+BC^2} \\ & =\sqrt{5^2+4^2} \\ AC &= \sqrt{41} \end{align}$
Jadi, jarak titik A ke titik C adalah $\sqrt{41}$ cm.
b. Jarak antara titik E dan C
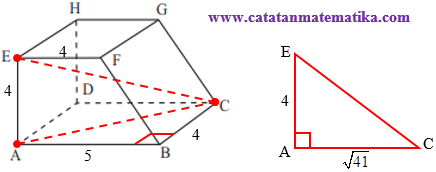
Jarak antara titik E dan C adalah panjang ruas garis CE.
Perhatikan segitiga AEC, siku-siku di A maka:
$\begin{align} CE &=\sqrt{AC^2+AE^2} \\ & =\sqrt{(\sqrt{41})^2+4^2} \\ CE &=\sqrt{57} \end{align}$
Jadi, jarak titik E ke titik C adalah $\sqrt{57}$.
c. Jarak antara titik A dan G
Jarak antara titik A dan G adalah panjang ruas garis AG.
Perhatikan segitiga EHG.
$\begin{align} EG &=\sqrt{EH^2+HG^2} \\ &=\sqrt{4^2+4^2} \\ EG &=\sqrt{32} \end{align}$
Perhatikan segitiga AEG.
$\begin{align} AG &=\sqrt{AE^2+EG^2} \\ &=\sqrt{4^2+(\sqrt{32})^2} \\ &=\sqrt{48} \\ AG &=4\sqrt{3} \end{align}$
Jadi, jarak titik A ke titik G adalah $4\sqrt{3}$ cm.
Contoh. 4
Diketahui balok ABCD.EFGH dengan AB = 8 cm, BC = 6 cm, dan BF = 24 cm. Jarak titik H ke titik B adalah ….
Penyelesaian:
Perhatikan gambar berikut!
Jarak titik H ke titik B adalah panjang ruas garis HB.
Perhatikan segitiga BAD, siku-siku di titik A, dengan teorema pythagoras maka:
$\begin{align}BD &=\sqrt{AB^2+AD^2} \\ &=\sqrt{8^2+6^2} \\ &=\sqrt{64+36} \\ BD &=10 \end{align}$
Perhatikan segitiga BDH, siku-siku di titik D, dengan teorema pythagoras maka:
$\begin{align}HB &=\sqrt{BD^2+DH^2} \\ &=\sqrt{{10}^2+{24}^2} \\ &=\sqrt{100+576} \\ &=\sqrt{676} \\ HB &=26 \end{align}$
Jadi, jarak titik H ke titik B adalah 26 cm.
Cara alternatif:
HB adalah diagonal ruang balok, maka:
$\begin{align}HB &=\sqrt{p^2+l^2+t^2} \\ &=\sqrt{8^2+6^2+{24}^2} \\ &=\sqrt{64+36+576} \\ &=\sqrt{676} \\ HB &=26 \end{align}$
Contoh 5.
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P, Q, dan R berturut-turut terletak pada pertengahan garis AB, BC, dan bidang ADHE. Tentukan jarak dari titik P ke titik R dan jarak dari titik Q ke titik R.Penyelesaian:
Jarak titik P ke titik R
Perhatikan gambar berikut!
AH adalah diagonal sisi kubus, maka:
$AH=s\sqrt{2}=6\sqrt{2}$
$\begin{align}AR &=\frac{1}{2}.AH \\ &=\frac{1}{2}.6\sqrt{2} \\ AR &=3\sqrt{2} \end{align}$
Perhatikan segitiga RAP, siku-siku di titik A maka:
$\begin{align}PR &=\sqrt{AP^2+AR^2}\\ &=\sqrt{3^2+(3\sqrt{2})^2} \\ &=\sqrt{9+18} \\ &=\sqrt{27} \\ PR &=3\sqrt{3} \end{align}$
Jadi, jarak titik P ke titik R adalah $3\sqrt{3}$ cm.
Jarak titik Q ke titik R
Perhatikan gambar berikut!
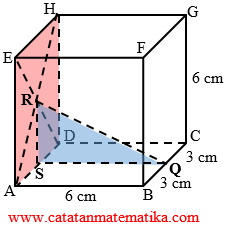
Perhatikan segitiga RSQ, siku-siku di titik S.
RS = 3 cm, SQ = 6 cm maka:
$\begin{align}QR &=\sqrt{RS^2+SQ^2} \\ &=\sqrt{3^2+6^2} \\ &=\sqrt{9+36} \\ &=\sqrt{45} \\ QR &=3\sqrt{5} \end{align}$
Jadi, jarak titik Q ke titik R adalah $3\sqrt{5}$ cm.
C. Soal Latihan
- Diketahui kubus ABCD.EFGH dengan titik K terletak pada perpanjangan CG sehingga GK = 4 cm. Garis DK memotong rusuk GH pada titik L. Jika panjang rusuk kubus adalah 6 cm, maka jarak titik L ke titik B adalah … cm.
- Prisma tegak segitiga sama sisi ABC.DEF dengan panjang AB = 6 cm dan AD = 12 cm. Jika titik G terletak di tengah-tengah sisi EF, maka panjang AG = … cm.
- Pada kubus ABCD.EFGH dengan panjang rusuk 8 cm. Titik P pertengahan rusuk EH. Jika titik Q di tengah-tengah garis CP, maka jarak titik A ke Q adalah … cm.
- Diketahui balok ABCD.EFGH dengan AB = 12 cm, BC = 3 cm, dan AE = 4 cm, maka jarak titik D ke titik F adalah ... cm
- Diketahui kubus PQRS.TUVW dengan rusuk $6\sqrt{2}$ cm, maka jarak titik R ke titik W adalah ... cm
Semoga postingan: Dimensi Tiga 1. Jarak Titik ke Titik pada Bangun Ruang ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.
Post a Comment for "Dimensi Tiga 1. Jarak Titik ke Titik pada Bangun Ruang"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.