Dimensi Tiga 4. Jarak Dua Garis Bersilangan
Jarak Dua Garis Bersilangan
(1) Garis $g$ dan $h$ bersilangan sebarang. AB adalah jarak antara garis $g$ dan $h$.

(2) Garis $g$ dan $h$ bersilangan tegak lurus. AB adalah jarak antara garis $g$ dan $h$.

a. jarak garis CG dan HB
b. jarak garis CG dan EF
Pembahasan:
a. Jarak antara garis CG dan HB dilukis sebagai berikut:
1) Buat garis HB
2) Buat bidang ACGE dan BDHF, dengan perpotongannya adalah garis PQ.
3) Garis PQ memotong garis HB di S.
4) Buat garis melalui titik S sejajar garis AC dan EG hingga memotong rusuk CG di R.
Perhatikan gambar berikut!
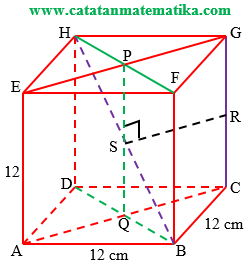
Ruas garis RS adalah jarak antara garis CG dan HB yang diminta.
$\begin{align} RS &=QC \\ & =\frac{1}{2}AC \\ & =\frac{1}{2}\sqrt{A{{B}^{2}}+B{{C}^{2}}} \\ & =\frac{1}{2}\sqrt{{{12}^{2}}+{{12}^{2}}} \\ RS &=6\sqrt{2} \end{align}$
Jadi, jarak antara garis CG dan HB adalah $6\sqrt{2}$ cm.
b. Jarak antara garis CG dan EF
Perhatikan gambar!
Garis CG tegak lurus garis FG
Garis EF tegak lurus FG
Jadi, CG dan EF adalah dua garis bersilangan yang saling tegak lurus, maka kita peroleh jarak garis CG dan garis EF adalah panjang ruas garis FG yaitu 12 cm.
Pembahasan:

Perhatikan segitiga ABC
$\begin{align} OC & =\frac{1}{2}AC \\ &= \frac{1}{2}\sqrt{A{{B}^{2}}+B{{C}^{2}}} \\ &=\frac{1}{2}\sqrt{{{(6\sqrt{2})}^{2}}+{{(6\sqrt{2})}^{2}}} \\ OC &=6 \end{align}$
Perhatikan segitiga TOC
$\begin{align} TO &=\sqrt{T{{C}^{2}}-O{{C}^{2}}} \\ &=\sqrt{{{10}^{2}}-{{6}^{2}}} \\ TO &= 8 \end{align}$
Luas segitiga TOC:
$\begin{align} \frac{1}{2}TC\times OE &= \frac{1}{2}OC\times TO \\ 10\times OE &= 6\times 8 \\ OE &= \frac{48}{10} \\ OE &= 4,8 \end{align}$
Jadi, jarak antara titik BD ke TC adalah 4,8 cm.
Pembahasan:
*) Buat bidang HDKL, bidang yang tegak lurus AC. AC menembus bidang HDKL di Q.
*) Perpanjang garis HP menjadi HM.
*) Proyeksikan HM di bidang HDKL, yaitu berada di garis HN.
*) Jarak AC ke HP adalah jarak Q ke HN.
Perhatikan gambar berikut:
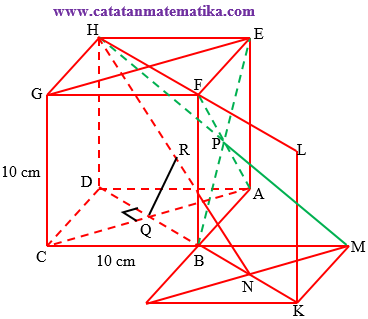
Perhatikan $\Delta HDN$

$\begin{align} HN &=\sqrt{D{{N}^{2}}+H{{D}^{2}}} \\ & =\sqrt{{{(15\sqrt{2})}^{2}}+{{10}^{2}}} \\ & =\sqrt{550} \\ HN &=5\sqrt{22} \end{align}$
$\Delta HDN\approx \Delta QRN$ maka:
$\frac{QR}{HD}=\frac{QN}{HN}$
$\frac{QR}{10}=\frac{10\sqrt{2}}{5\sqrt{22}}$
$QR=\frac{20}{\sqrt{11}}$
$QR=\frac{20}{11}\sqrt{11}$
Jarak antara garis $g$ dan $h$ yang bersilangan adalah panjang garis potong tegak lurus persekutuan kedua garis itu, yaitu panjang ruas garis yang memotong kedua garis itu secara tegak lurus.
Untuk lebih jelasnya perhatikan gambar berikut.(1) Garis $g$ dan $h$ bersilangan sebarang. AB adalah jarak antara garis $g$ dan $h$.

(2) Garis $g$ dan $h$ bersilangan tegak lurus. AB adalah jarak antara garis $g$ dan $h$.

Soal dan Pembahasan:
Contoh 1.
Diberikan kubus ABCD.EFGH dengan panjang rusuk 12 cm. Tentukan:a. jarak garis CG dan HB
b. jarak garis CG dan EF
Pembahasan:
a. Jarak antara garis CG dan HB dilukis sebagai berikut:
1) Buat garis HB
2) Buat bidang ACGE dan BDHF, dengan perpotongannya adalah garis PQ.
3) Garis PQ memotong garis HB di S.
4) Buat garis melalui titik S sejajar garis AC dan EG hingga memotong rusuk CG di R.
Perhatikan gambar berikut!

Ruas garis RS adalah jarak antara garis CG dan HB yang diminta.
$\begin{align} RS &=QC \\ & =\frac{1}{2}AC \\ & =\frac{1}{2}\sqrt{A{{B}^{2}}+B{{C}^{2}}} \\ & =\frac{1}{2}\sqrt{{{12}^{2}}+{{12}^{2}}} \\ RS &=6\sqrt{2} \end{align}$
Jadi, jarak antara garis CG dan HB adalah $6\sqrt{2}$ cm.
b. Jarak antara garis CG dan EF
Perhatikan gambar!
Garis CG tegak lurus garis FG
Garis EF tegak lurus FG
Jadi, CG dan EF adalah dua garis bersilangan yang saling tegak lurus, maka kita peroleh jarak garis CG dan garis EF adalah panjang ruas garis FG yaitu 12 cm.
Contoh 2.
Diberikan limas segi empat beraturan T.ABCD, dengan AB = $6\sqrt{2}$ dan TA = 10 cm. Hitunglah jarak antara garis BD dan TC.Pembahasan:

Perhatikan segitiga ABC
$\begin{align} OC & =\frac{1}{2}AC \\ &= \frac{1}{2}\sqrt{A{{B}^{2}}+B{{C}^{2}}} \\ &=\frac{1}{2}\sqrt{{{(6\sqrt{2})}^{2}}+{{(6\sqrt{2})}^{2}}} \\ OC &=6 \end{align}$
Perhatikan segitiga TOC
$\begin{align} TO &=\sqrt{T{{C}^{2}}-O{{C}^{2}}} \\ &=\sqrt{{{10}^{2}}-{{6}^{2}}} \\ TO &= 8 \end{align}$
Luas segitiga TOC:
$\begin{align} \frac{1}{2}TC\times OE &= \frac{1}{2}OC\times TO \\ 10\times OE &= 6\times 8 \\ OE &= \frac{48}{10} \\ OE &= 4,8 \end{align}$
Jadi, jarak antara titik BD ke TC adalah 4,8 cm.
Contoh 3.
Titik P merupakan titik potong antara garis AF dan BE pada kubus ABCD.EFGH yang berusuk 1 dm, maka jarak antara HP dan AC adalah … cm.Pembahasan:
*) Buat bidang HDKL, bidang yang tegak lurus AC. AC menembus bidang HDKL di Q.
*) Perpanjang garis HP menjadi HM.
*) Proyeksikan HM di bidang HDKL, yaitu berada di garis HN.
*) Jarak AC ke HP adalah jarak Q ke HN.
Perhatikan gambar berikut:

Perhatikan $\Delta HDN$

$\begin{align} HN &=\sqrt{D{{N}^{2}}+H{{D}^{2}}} \\ & =\sqrt{{{(15\sqrt{2})}^{2}}+{{10}^{2}}} \\ & =\sqrt{550} \\ HN &=5\sqrt{22} \end{align}$
$\Delta HDN\approx \Delta QRN$ maka:
$\frac{QR}{HD}=\frac{QN}{HN}$
$\frac{QR}{10}=\frac{10\sqrt{2}}{5\sqrt{22}}$
$QR=\frac{20}{\sqrt{11}}$
$QR=\frac{20}{11}\sqrt{11}$

Cara yang jarak CG dan EF gimana kak??
ReplyDeleteoh iya, tuh sudah diupdate pembahasannya. Terima kasih telah berkunjung.
DeleteLuar biasa mas
ReplyDelete