Skip to content Skip to sidebar Skip to footer

Home / Bank Soal / Matematika Wajib Kelas 10 / Trigonometri

Soal Luas Segitiga dan Pembahasan

1 comment
Berikut ini adalah Soal-Soal Luas Segitiga dan Pembahasan. Silahkan dipelajari dan jangan lupa share/bagikan ke media sosial kalian, agar manfaat postingan ini dapat dirasakan oleh siswa/i yang lain. Terima kasih.
Tata Cara Belajar:
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cocokkanlah jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "Lihat/Tutup:".
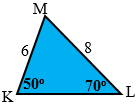
Soal No. 1
Luas segitiga di bawah ini adalah …
Luas Segitiga
(A) $4\sqrt{3}$
(B) $6\sqrt{3}$
(C) $8\sqrt{3}$
(D) $10\sqrt{3}$
(E) $12\sqrt{3}$
Penyelesaian: Lihat/Tutup Pada segitiga KLM maka berlaku:
$\begin{align}K+L+M &=180{}^\circ \\ 50{}^\circ +70{}^\circ +M &=180{}^\circ \\ 120{}^\circ +M &=180{}^\circ \\ M &=60{}^\circ \end{align}$
$l=6$ dan $k=8$
$\begin{align}\left[ KLM \right] &=\frac{1}{2}k.l.\sin M \\ &=\frac{1}{2}.8.6.\sin 60{}^\circ \\ &=24.\frac{1}{2}\sqrt{3} \\ \left[ KLM \right] &=12\sqrt{3} \end{align}$
Jawaban: E
Soal No. 2
Dalam sebuah segitiga ABC, diketahui a = 16 cm, b = 10 cm dan luasnya 40 $\text{c}{{\text{m}}^{\text{2}}}$. Besar sudut apit sisi a dan b adalah ….
(A) $75{}^\circ $
(B) $60{}^\circ $
(C) $80{}^\circ $
(D) $30{}^\circ $
(E) $15{}^\circ $
Penyelesaian: Lihat/Tutup L = 40, a = 16, b = 10, $\angle (a,b)=\angle C$ = …
$\begin{align} L &=\frac{1}{2}ab\sin C \\ 40 &=\frac{1}{2}.16.10.\sin C \\ 40 &=80.\sin C \\ \frac{40}{80} &=\sin C \\ \sin C &=\frac{1}{2} \\ C &=30{}^\circ \end{align}$
Jawaban: D
Soal No. 3
Pada segitiga ABC dengan panjang BC = 16 cm, AC = 10 cm, dan luas $\Delta ABC=40\sqrt{3}$ cm, maka panjang AB = … cm.
(A) 15
(B) 14
(C) 13
(D) 12
(E) 11
Penyelesaian: Lihat/Tutup BC = a = 16 cm
AC = b = 10 cm
L = $40\sqrt{3}$
$\begin{align} L &=\frac{1}{2}ab.\sin C \\ 40\sqrt{3} &=\frac{1}{2}.16.10.\sin C \\ 40\sqrt{3} &=80\sin C \\ \frac{40\sqrt{3}}{80} &=\sin C \\ \sin C &=\frac{1}{2}\sqrt{3} \\ C &=60{}^\circ \end{align}$
dengan Aturan Cosinus maka:
$\begin{align}{{c}^{2}} &={{a}^{2}}+{{b}^{2}}-2ab.\cos C \\ &={{16}^{2}}+{{10}^{2}}-2.16.10.\cos 60{}^\circ \\ &=256+100-320.\frac{1}{2} \\ &=356-160 \\ {{c}^{2}} &=196 \\ c &=14 \end{align}$
Jadi, panjang AB = c = 14 cm.
Jawaban: B
Soal No. 4
Jajaran genjang ABCD, diketahui AB = 5 cm, BC = 4 cm, dan $\angle ABC=120{}^\circ $, maka luas jajaran genjang itu sama dengan … satuan luas.
(A) $5\sqrt{3}$
(B) 10
(C) 20
(D) $10\sqrt{3}$
(E) $20\sqrt{3}$
Penyelesaian: Lihat/Tutup Perhatikan gambar berikut!
Luas jajaran genjang ABCD
$\begin{align} \left[ ABCD \right] &=2\times \left[ ABC \right] \\ &=2\times \frac{1}{2}.AB.BC.\sin \angle ABC \\ &=5.4.\sin 120{}^\circ \\ &=20.\sin (180{}^\circ -60{}^\circ ) \\ &=20\sin 60{}^\circ \\ &=20.\frac{1}{2}\sqrt{3} \\ \left[ ABCD \right] &=10\sqrt{3} \end{align}$
Jawaban: D
Soal No. 5
Layang-layang garis singgung OAPB, sudut APB = $60{}^\circ $ dan panjang OP = 20 cm. Luas OAPB = … $\text{c}{{\text{m}}^{\text{2}}}$.
Luas layang-layang
(A) 100
(B) $100\sqrt{2}$
(C) $100\sqrt{3}$
(D) 200
(E) $100\sqrt{5}$
Penyelesaian: Lihat/Tutup $\angle APB=60{}^\circ $
$\begin{align} \angle OPA &=\frac{1}{2}.\angle APB \\ &=\frac{1}{2}.60{}^\circ \\ \angle OPA &=30{}^\circ \end{align}$
Karena AP adalah garis singgung lingkaran maka $OA\bot AP$.
Untuk lebih jelasnya perhatikan segitiga OAP:
Luas segitiga
$\begin{align}\left[ OAP \right] &=\frac{{{a}^{2}}.\sin \angle P.\sin \angle O}{2.\sin \angle A} \\ &=\frac{{{20}^{2}}.\sin 30{}^\circ .\sin 60{}^\circ }{2.\sin 90{}^\circ } \\ &=\frac{400.\frac{1}{2}.\frac{1}{2}\sqrt{3}}{2.1} \\ \left[ OAP \right] &=50\sqrt{3} \end{align}$
Luas layang-layang OAPB adalah:
$\begin{align} \left[ OAPB \right] &=2\times \left[ OAP \right] \\ &=2\times 50\sqrt{3} \\ \left[ OAPB \right] &=100\sqrt{3} \end{align}$
Jawaban: C
Soal No. 6
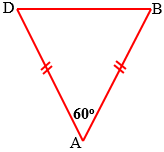
Perhatikan gambar berikut!
Luas layang-layang ABCD
Diketahui AB = AD, BC = CD = 4 cm, $\angle A=60{}^\circ $ dan $\angle C=120{}^\circ $. Luas segiempat ABCD adalah … $\text{c}{{\text{m}}^{\text{2}}}$.
(A) $4\sqrt{3}$
(B) $8\sqrt{3}$
(C) $12\sqrt{3}$
(D) $16\sqrt{3}$
(E) $18\sqrt{3}$
Penyelesaian: Lihat/Tutup Perhatikan segitiga DBC:
Luas segitiga sama kaki
Aturan Cosinus:
$\begin{align}B{{D}^{2}} &=B{{C}^{2}}+C{{D}^{2}}-2.BC.CD.\cos \angle BCD \\ &={{4}^{2}}+{{4}^{2}}-2.4.4.\cos 120{}^\circ \\ &=16+16-32.\left( -\frac{1}{2} \right) \\ &=32+16 \\ B{{D}^{2}} &=48 \\ BD &=\sqrt{48}=4\sqrt{3} \end{align}$
Luas segitiga BCD:
$\begin{align}{{L}_{BCD}} &=\frac{1}{2}.BC.CD.\sin C \\ &=\frac{1}{2}.4.4.\sin 120{}^\circ \\ &=8.\sin (180{}^\circ -60{}^\circ ) \\ &=8.\sin 60{}^\circ \\ &=8.\frac{1}{2}\sqrt{3} \\ {{L}_{BCD}} &=4\sqrt{3} \end{align}$
Perhatikan segitiga ABD:
Luas segitiga sama sisi
karena AB = AD dan $\angle A=60{}^\circ $ maka segitiga ABD segitiga sama sisi.
AB = AD = BD = $4\sqrt{3}$
Luas ABD adalah:
$\begin{align} {{L}_{ABD}} &=\frac{1}{2}.AB.AD.\sin A \\ &=\frac{1}{2}.4\sqrt{3}.4\sqrt{3}.\sin 60{}^\circ \\ &=24.\frac{1}{2}\sqrt{3} \\ {{L}_{ABD}} &=12\sqrt{3} \end{align}$
Jadi, luas ABCD adalah:
$\begin{align} {{L}_{ABCD}} &={{L}_{ABD}}+{{L}_{BCD}} \\ &=12\sqrt{3}+4\sqrt{3} \\ {{L}_{ABCD}} &=16\sqrt{3}\end{align}$
Jawaban: D
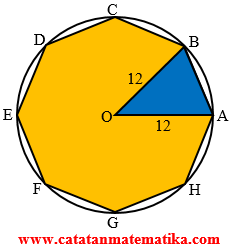
Soal No. 7
Titik-titik sudut suatu segidelapan beraturan dilukiskan dalam lingkaran yang berjari-jari 12 cm. Luas segidelapan beraturan itu sama dengan … $\text{c}{{\text{m}}^{\text{2}}}$.
(A) $288\sqrt{2}$
(B) $288\sqrt{3}$
(C) 288
(D) $144\sqrt{2}$
(E) $144\sqrt{3}$
Penyelesaian: Lihat/Tutup Perhatikan gambar segidelapan beraturan berikut ini!
Luas segi-8 beraturan
$\angle AOB=\frac{360{}^\circ }{8}=45{}^\circ $
$\begin{align}{{L}_{segidelapan}} &=8.{{L}_{AOB}} \\ &=8.\frac{1}{2}.OA.OB.\sin \angle AOB \\ &=4.12.12.\sin 45{}^\circ \\ &=576.\frac{1}{2}\sqrt{2} \\ {{L}_{segidelapan}} &=288\sqrt{2} \end{align}$
Jawaban: A
Soal No. 8
Luas segitiga beraturan dengan panjang sisi a satuan adalah …
(A) $\frac{1}{2}{{a}^{2}}\sqrt{2}$
(B) $\frac{1}{4}{{a}^{2}}\sqrt{2}$
(C) $\frac{3}{4}{{a}^{2}}\sqrt{2}$
(D) $\frac{1}{4}{{a}^{2}}\sqrt{3}$
(E) $\frac{3}{4}{{a}^{2}}\sqrt{3}$
Penyelesaian: Lihat/Tutup Perhatikan segitiga beraturan berikut!
Luas segitiga beraturan
Segitiga beraturan adalah segitiga sama sisi, maka semua sudutnya $60{}^\circ $.
$\begin{align}L &=\frac{1}{2}.AB.AC.\sin \angle BAC \\ &=\frac{1}{2}.a.a.\sin 60{}^\circ \\ &=\frac{1}{2}{{a}^{2}}.\frac{1}{2}\sqrt{3} \\ L &=\frac{1}{4}{{a}^{2}}\sqrt{3} \end{align}$
Jawaban: D
Soal No. 9
Jajaran genjang ABCD dengan AB = 6 cm dan AD = $2\sqrt{2}$ cm mempunyai luas 12 $\text{c}{{\text{m}}^{\text{2}}}$. Besar sudut A adalah ….
(A) $15{}^\circ $
(B) $30{}^\circ $
(C) $45{}^\circ $
(D) $60{}^\circ $
(E) $70{}^\circ $
Penyelesaian: Lihat/Tutup Perhatikan jajaran genjang ABCD berikut!
Luas jajaran genjang ABCD
Luas ABCD = 12 $\text{c}{{\text{m}}^{\text{2}}}$
Perhatikan segitiga ABD:
${{L}_{ABD}}=\frac{1}{2}.AB.AD.\sin A$
$\begin{align} {{L}_{ABD}} &=\frac{1}{2}\times {{L}_{ABCD}} \\ \frac{1}{2}.AB.AD.\sin A &=\frac{1}{2}\times 12 \\ \frac{1}{2}.6.2\sqrt{2}.\sin A &=6 \\ \sqrt{2}.\sin A &=1 \\ \sin A &=\frac{1}{\sqrt{2}} \\ \sin A &=\frac{1}{2}\sqrt{2} \\ A &=45{}^\circ \end{align}$
Jawaban: C
Soal No. 10
Diketahui segiempat PQRS dengan PS = 5 cm, PQ = 12 cm, QR = 8 cm, besar sudut SPQ = $90{}^\circ $, dan besar sudut SQR = $150{}^\circ $. Luas PQRS adalah … $\text{c}{{\text{m}}^{\text{2}}}$.
Luas segiempat PQRS
(A) 13
(B) 26
(C) 30
(D) 46
(E) 56
Penyelesaian: Lihat/Tutup Luas segiempat PQRS
Perhatikan segitiga SPQ, siku-siku di P maka:
$\begin{align}SQ &=\sqrt{S{{P}^{2}}+P{{Q}^{2}}} \\ &=\sqrt{{{5}^{2}}+{{12}^{2}}} \\ &=\sqrt{25+144} \\ &=\sqrt{169} \\ SQ &=13 \end{align}$
Luas segitiga SPQ:
$\begin{align}{{L}_{SPQ}} &=\frac{1}{2}.SP.PQ \\ &=\frac{1}{2}.5.12 \\ {{L}_{SPQ}} &=30 \end{align}$
Luas segitiga SQR:
$\begin{align}{{L}_{SQR}} &=\frac{1}{2}.SQ.QR.\sin \angle SQR \\ &=\frac{1}{2}.13.8.\sin 150{}^\circ \\ &=52.\sin (180{}^\circ -30{}^\circ ) \\ &=52.\sin 30{}^\circ \\ &=52.\frac{1}{2} \\ {{L}_{SQR}} &=26 \end{align}$
Luas PQRS adalah:
$\begin{align}{{L}_{PQRS}} &={{L}_{SPQ}}+{{L}_{SQR}} \\ &=30+26 \\ {{L}_{PQRS}} &=56 \end{align}$
Jawaban: E
Soal No. 11
Diketahui segitiga ABC dengan panjang AC = BC = 6, AB = $6\sqrt{3}$. Luas segitiga ABC tersebut adalah … satuan luas.
(A) $36\sqrt{3}$
(B) $18\sqrt{3}$
(C) $9\sqrt{3}$
(D) $9\sqrt{2}$
(E) $\frac{9}{2}\sqrt{2}$
Penyelesaian: Lihat/Tutup AC = BC = 6 maka segitiga ABC adalah segitiga sama kaki. Kemudian lukis garis tinggi CD sehingga diperoleh gambar seperti berikut ini.
Luas segitiga sama kaki
Perhatikan segitiga ADC, berlaku pythagoras:
$\begin{align} CD &=\sqrt{A{{C}^{2}}-A{{D}^{2}}} \\ &=\sqrt{{{6}^{2}}-{{(3\sqrt{3})}^{2}}} \\ &=\sqrt{36-27} \\ CD &=3 \end{align}$
$\begin{align}\left[ ABC \right] &=\frac{1}{2}alas\times tinggi \\ &=\frac{1}{2}.AB.CD \\ &=\frac{1}{2}.6\sqrt{3}.3 \\ \left[ ABC \right] &=9\sqrt{3} \end{align}$
Jawaban: C
Soal No. 12
Luas segitiga di bawah ini adalah …
Luas segitiga jika diketahui dua sisi dan sudut apitnya
(A) $2\sqrt{2}$
(B) $4\sqrt{2}$
(C) $6\sqrt{2}$
(D) $4\sqrt{3}$
(E) $6\sqrt{3}$
Penyelesaian: Lihat/Tutup Dari gambar diperoleh:
$q=4$, $r=6$ dan $\angle P=45{}^\circ $
$\begin{align}\left[ PQR \right] &=\frac{1}{2}qr\sin P \\ &=\frac{1}{2}.4.6.\sin 45{}^\circ \\ &=12.\frac{1}{2}\sqrt{2} \\ \left[ PQR \right] &=6\sqrt{2} \end{align}$
Jawaban: C
Soal No. 13
Diketahui segitiga ABC dengan panjang AB = 6 cm, besar $\angle A=30{}^\circ $ dan $\angle C=120{}^\circ $. Luas segitiga ABC adalah … $\text{c}{{\text{m}}^{\text{2}}}$.
(A) 18
(B) 9
(C) $6\sqrt{3}$
(D) $3\sqrt{3}$
(E) $2\sqrt{3}$
Penyelesaian: Lihat/Tutup Pada segitiga ABC:
$\begin{align} A+B+C &=180{}^\circ \\ 30{}^\circ +B+120{}^\circ &=180{}^\circ \\ B &=30{}^\circ \end{align}$
AB = c = 6 cm
$\begin{align}L &=\frac{{{c}^{2}}.\sin A.\sin B}{2\sin C} \\ &=\frac{{{6}^{2}}.\sin 30{}^\circ .\sin 30{}^\circ }{2\sin 120{}^\circ } \\ &=\frac{36.\frac{1}{2}.\frac{1}{2}}{2.\frac{1}{2}\sqrt{3}} \\ &=\frac{9}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ L &=3\sqrt{3} \end{align}$
Jawaban: D
Soal No. 14
Segitiga XYZ mempunyai panjang rusuk x = 4 cm, y = 5 cm, dan z = 7 cm. Luas segitiga XYZ adalah …
(A) $2\sqrt{6}$
(B) $3\sqrt{6}$
(C) $4\sqrt{6}$
(D) $5\sqrt{6}$
(E) $6\sqrt{6}$
Penyelesaian: Lihat/Tutup $\begin{align}s &=\frac{1}{2}(x+y+z) \\ &=\frac{1}{2}(4+5+7) \\ s &=8 \end{align}$
$\begin{align}L &=\sqrt{s(s-x)(s-y)(s-z)} \\ &=\sqrt{8(8-4)(8-5)(8-7)} \\ &=\sqrt{8.4.3.1} \\ &=\sqrt{96} \\ &=\sqrt{16\times 6} \\ L &=4\sqrt{6} \end{align}$
Jawaban: C
Soal No. 15
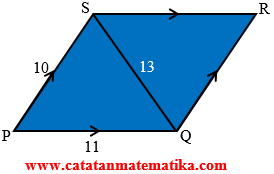
Jajaran genjang PQRS diketahui PQ = 11 cm; PS = 10 cm dan QS = 13 cm. Luas jajaran genjang tersebut adalah ….
(A) 103,88
(B) 104,88
(C) 105,88
(D) 106,88
(E) 107,88
Penyelesaian: Lihat/Tutup Luas jajaran genjang PQRS
Perhatikan segitiga PQS:
$s=\frac{1}{2}(10+11+13)=17$
$\begin{align}{{L}_{PQS}} &=\sqrt{17(17-11)(17-10)(17-13)} \\ &=\sqrt{17.6.7.4} \\ &=\sqrt{2856} \\ {{L}_{PQS}} &=53,44 \end{align}$
$\begin{align}{{L}_{PQRS}} &=2\times {{L}_{PQS}} \\ &=2\times 53,44 \\ {{L}_{PQRS}} &=106,88 \end{align}$
Jawaban: D
Semoga postingan: Soal Luas Segitiga dan Pembahasan ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Subscribe and Follow Our Channel:
Youtube Catatan Matematika
Tiktok Catatan Matematika
Instagram Catatan Matematika
Facebook Catatan Matematika

1 comment for "Soal Luas Segitiga dan Pembahasan"

Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.

Pantun Matematika: