Soal Grafik Fungsi Trigonometri dan Pembahasan

Berikut ini adalah Soal-Soal Grafik Fungsi Trigonometri, yaitu salah satu sub materi TRIGONOMETRI pada mata pelajaran Matematika Wajib Kelas 10. Silahkan dipelajari dan jangan lupa share/bagikan ke media sosial kalian, agar manfaat postingan ini dapat dirasakan oleh siswa/i yang lain. Terima kasih.

Tata Cara Belajar:
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cocokkanlah jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "Lihat/Tutup:".

Soal No. 1

Amplitudo dan periode dari grafik berikut adalah ….

(A) 2 dan $\pi $
(B) 4 dan $2\pi $
(C) 1 dan $\frac{\pi }{2}$
(D) 2 dan $2\pi $
(E) 2 dan $\frac{\pi }{2}$

Penyelesaian: Lihat/Tutup

Dari grafik:
${{y}_{\text{maks}}}=2$
${{y}_{\text{min}}}=-2$
Amplitudo (A) adalah:
$\begin{align}A &=\frac{1}{2}\left( {{y}_{\text{maks}}}-{{y}_{\text{min}}} \right) \\ &=\frac{1}{2}\left( 2-(-2) \right) \\ &=\frac{1}{2}.4 \\ A &=2 \end{align}$
Periode (p) dimulai dari 0 sampai $2\pi $ maka $p=2\pi -0\Leftrightarrow p=2\pi $
Jadi, amplitudo dan periode dari grafik fungsi tersebut adalah 2 dan $2\pi $.
Jawaban: D

---

Soal No. 2

Grafik di bawah ini mempunyai persamaan fungsi …

(A) $y=-2\sin x$
(B) $y=2\sin x$
(C) $y=2\cos x$
(D) $y=-2\cos x$
(E) $y=\sin 2x$

Penyelesaian: Lihat/Tutup

Dari grafik dan opsi dapat kita tentukan untuk sementara bahwa persamaannya adalah $y=A\sin kx$.
${{y}_{\text{maks}}}=2$ dan ${{y}_{\text{min}}}=-2$
$\begin{align}A &=\frac{1}{2}\left( {{y}_{\text{maks}}}-{{y}_{\text{min}}} \right) \\ &=\frac{1}{2}\left( 2-(-2) \right) \\ &=\frac{1}{2}.4 \\ A &=2 \end{align}$
Periode (p) dimulai dari 0 sampai $2\pi $ maka p = $2\pi $.
Ingat periode fungsi sinus adalah:
$\begin{align}p &=\frac{2\pi }{k} \\ 2\pi &=\frac{2\pi }{k} \\ k &=\frac{2\pi }{2\pi } \\ k &=1 \end{align}$
Jadi, persamaan grafik tersebut adalah $y=A\sin kx\Leftrightarrow y=2\sin x$.
Jawaban: B

---

Soal No. 3

Persamaan untuk kurva di bawah ini adalah ….

(A) $y=3\sin \frac{3}{2}x$
(B) $y=3\sin \frac{2}{3}x$
(C) $y=3\sin 3x$
(D) $y=3\cos \frac{3}{2}x$
(E) $y=3\cos \frac{2}{3}x$

Penyelesaian: Lihat/Tutup

Dari grafik dan opsi dapat kita tentukan bahwa persamaan fungsi grafik adalah $y=A\sin kx$.
${{y}_{\text{maks}}}=3$ dan ${{y}_{\text{min}}}=-3$
$\begin{align}A &=\frac{1}{2}\left( {{y}_{\text{maks}}}-{{y}_{\text{min}}} \right) \\ &=\frac{1}{2}\left( 3-(-3) \right) \\ &=\frac{1}{2}.6 \\ A &=3 \end{align}$
Periode (p) dimulai dari 0 sampai $3\pi $ maka p = $3\pi $.
Ingat periode fungsi sinus adalah:
$\begin{align}p &=\frac{2\pi }{k} \\ 3\pi &=\frac{2\pi }{k} \\ k &=\frac{2\pi }{3\pi } \\ k &=\frac{2}{3} \end{align}$
Jadi, persamaan grafik tersebut adalah $y=A\sin kx\Leftrightarrow y=3\sin \frac{2}{3}x$.
Jawaban: B

---

Soal No. 4

Persamaan untuk kurva di samping adalah ….

(A) $y=-2\tan 2x$
(B) $y=-2\tan x$
(C) $y=-2\tan \frac{1}{2}x$
(D) $y=2\tan 2x$
(E) $y=2\tan x$

Penyelesaian: Lihat/Tutup

Dari grafik dan opsi dapat kita tentukan untuk sementara persamaan grafik fungsi tersebut adalah $y=2\tan kx$.
Periode (p) dimulai dari $-\frac{\pi }{4}$ sampai $\frac{\pi }{4}$ maka:
$p=\frac{\pi }{4}-\left( -\frac{\pi }{4} \right)\Leftrightarrow p=\frac{\pi }{2}$
Ingat periode fungsi tangen adalah:
$\begin{align}p &=\frac{\pi }{k} \\ \frac{\pi }{2} &=\frac{\pi }{k} \\ k &=2 \end{align}$
Jadi, persamaan grafik tersebut adalah $y=2\tan kx\Leftrightarrow y=2\tan 2x$
Jawaban: D

---

Soal No. 5

Grafik fungsi di bawah ini mempunyai persamaan ….

(A) $y=2\sin \left( x-\frac{1}{2}\pi \right)$
(B) $y=2\sin \left( \frac{1}{2}\pi -x \right)$
(C) $y=2\sin \left( 2x+\frac{1}{2}\pi \right)$
(D) $y=-2\sin \left( \frac{1}{2}\pi +x \right)$
(E) $y=-2\sin \left( \frac{1}{2}\pi -2x \right)$

Penyelesaian: Lihat/Tutup

Dari grafik dan opsi dapat kita tentukan untuk sementara persamaan grafik fungsi tersebut adalah $y=A\sin (kx+b)$.
${{y}_{\text{maks}}}=2$ dan ${{y}_{\text{min}}}=-2$
$\begin{align}A &=\frac{1}{2}\left( {{y}_{\text{maks}}}-{{y}_{\text{min}}} \right) \\ &=\frac{1}{2}\left( 2-(-2) \right) \\ &=\frac{1}{2}.4 \\ A &=2 \end{align}$
Periode (p) dimulai dari $-\frac{3}{4}\pi $ sampai $\frac{1}{4}\pi $, maka $p=\frac{1}{4}\pi -\left( -\frac{3}{4}\pi \right)\Leftrightarrow p=\pi $
Ingat periode fungsi sinus adalah:
$\begin{align} p &=\frac{2\pi }{k} \\ \pi &=\frac{2\pi }{k} \\ k &=\frac{2\pi }{\pi } \\ k &=2 \end{align}$
Grafik melalui titik $\left( \frac{1}{2}\pi ,2 \right)$, maka:
$\begin{align}y &=A\sin (kx+b) \\ y &=2\sin (2x+b) \\ 2 &=2\sin \left( 2.\frac{1}{2}\pi +b \right) \\ 1 &=\sin \left( \pi +b \right) \\ \sin \frac{1}{2}\pi &=\sin \left( \pi +b \right) \\ \frac{1}{2}\pi &=\pi +b \\ b &=\frac{1}{2}\pi -\pi \\ b &=-\frac{1}{2}\pi \end{align}$
Jadi, persamaan grafik tersebut adalah:
$\begin{align}y &=A\sin (kx+b) \\ y &=2\sin \left( 2x-\frac{1}{2}\pi \right) \\ y &=2\sin -\left( \frac{1}{2}\pi -2x \right) \\ y &=-2\sin \left( \frac{1}{2}\pi -2x \right) \end{align}$
Jawaban: E

---

Soal No. 6

Sketsa grafik di bawah ini adalah sebagian dari grafik fungsi trigonometri yang persamaannya adalah ….

(A) $y=2\cos 2x$
(B) $y=4\sin x$
(C) $y=4\cos x$
(D) $y=4\sin \frac{1}{2}x$
(E) $y=4\cos \frac{1}{2}x$

Penyelesaian: Lihat/Tutup

Dari grafik dan opsi dapat kita tentukan untuk sementara persamaannya adalah $y=A\cos kx$.
${{y}_{\text{maks}}}=4$ dan ${{y}_{\text{min}}}=-4$
$\begin{align}A &=\frac{1}{2}\left( {{y}_{\text{maks}}}-{{y}_{\text{min}}} \right) \\ &=\frac{1}{2}\left( 4-(-4) \right) \\ A &=4 \end{align}$
Periode (p) dimulai dari $0{}^\circ $ sampai dengan $720{}^\circ $, maka $p=720{}^\circ -0{}^\circ \Leftrightarrow p=720{}^\circ $.
Ingat periode fungsi cosinus adalah:
$\begin{align}p &=\frac{360{}^\circ }{k} \\ 720{}^\circ &=\frac{360{}^\circ }{k} \\ k &=\frac{360{}^\circ }{720{}^\circ } \\ k &=\frac{1}{2} \end{align}$
Jadi, persamaan grafik tersebut adalah $y=A\cos kx\Leftrightarrow y=4\cos \frac{1}{2}x$.
Jawaban: E

---

Soal No. 7

Persamaan grafik di bawah ini adalah ….

(A) $y=2\sin (x-90{}^\circ )$
(B) $y=\sin (2x-90{}^\circ )$
(C) $y=2\sin (x+90{}^\circ )$
(D) $y=\sin (2x+90{}^\circ )$
(E) $y=2\sin (2x+180{}^\circ )$

Penyelesaian: Lihat/Tutup

Dari grafik dan opsi maka dapat kita tentukan untuk sementara persamaannya adalah $y=A\sin (kx+b)$
${{y}_{\text{maks}}}=2$ dan ${{y}_{\text{min}}}=-2$
$\begin{align}A &=\frac{1}{2}\left( {{y}_{\text{maks}}}-{{y}_{\text{min}}} \right) \\ &=\frac{1}{2}\left( 2-(-2) \right) \\ A &=2 \end{align}$
Periode (p) = $360{}^\circ $
Ingat periode fungsi sinus adalah:
$\begin{align}p &=\frac{360{}^\circ }{k} \\ 360{}^\circ &=\frac{360{}^\circ }{k} \\ k &=1 \end{align}$
$y=A\sin (kx+b)\Leftrightarrow y=2\sin (x+b)$
Melalui titik $\left( 0{}^\circ ,2 \right)$ maka:
$\begin{align}y &=2\sin (x+b) \\ 2 &=2\sin (0{}^\circ +b) \\ 1 &=\sin b \\ \sin 90{}^\circ &=\sin b \\ b &=90{}^\circ \end{align}$
Jadi, persamaan grafik tersebut adalah$y=2\sin (x+b)\Leftrightarrow y=2\sin (x+90{}^\circ )$.
Jawaban: C

---

Soal No. 8

Persamaan grafik di bawah ini adalah $y=a\cos kx$, untuk $0{}^\circ \le x\le 120{}^\circ $. Nilai $a$ dan $k$ berturut-turut adalah ….

(A) $-2$ dan $\frac{1}{6}$
(B) 2 dan 3
(C) 2 dan $\frac{1}{3}$
(D) $-2$ dan 3
(E) $-2$ dan $\frac{1}{3}$

Penyelesaian: Lihat/Tutup

$y=a\cos kx$
${{y}_{\text{maks}}}=2$ dan ${{y}_{\min }}=-2$
$\begin{align}a &=\frac{1}{2}\left( {{y}_{\text{maks}}}-{{y}_{\text{min}}} \right) \\ &=\frac{1}{2}\left( 2-(-2) \right) \\ a &=2 \end{align}$
Periode (p) = $120{}^\circ $
Ingat periode fungsi cosinus adalah:
$\begin{align}p &=\frac{360{}^\circ }{k} \\ 120{}^\circ &=\frac{360{}^\circ }{k} \\ k &=\frac{360{}^\circ }{120{}^\circ } \\ k &=3 \end{align}$
Nilai $a$ dan $k$ berturut-turut adalah 2 dan 3.
Jawaban: B

---

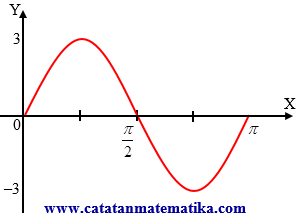
Soal No. 9

Persamaan fungsi trigonometri pada gambar grafik adalah …

(A) $y=\sin x$
(B) $y=2\sin 3x$
(C) $y=3\sin 4x$
(D) $y=3\sin 2x$
(E) $y=3\sin \frac{1}{2}x$

Penyelesaian: Lihat/Tutup

Berdasarkan grafik dan opsi untuk sementara dapat kita tentukan persamaannya adalah $y=A\sin kx$.
${{y}_{\text{maks}}}=3$ dan ${{y}_{\min }}=-3$
$\begin{align}a &=\frac{1}{2}\left( {{y}_{\text{maks}}}-{{y}_{\text{min}}} \right) \\ &=\frac{1}{2}\left( 3-(-3) \right) \\ a &=3 \end{align}$
Periode (p) = $\pi $
Ingat periode fungsi sinus adalah:
$\begin{align} p &=\frac{2\pi }{k} \\ \pi &=\frac{2\pi }{k} \\ k &=\frac{2\pi }{\pi } \\ k &=2 \end{align}$
Jadi, persamaan fungsi trigonometri pada grafik tersebut adalah $y=A\sin kx\Leftrightarrow y=3\sin 2x$.
Jawaban: D

---

Soal No. 10

Perhatikan gambar berikut!

Persamaan grafik fungsi pada gambar adalah ….
(A) $y=-2\sin (3x+45{}^\circ )$
(B) $y=-2\sin (3x-15{}^\circ )$
(C) $y=-2\sin (3x-45{}^\circ )$
(D) $y=2\sin (3x+15{}^\circ )$
(E) $y=2\sin (3x-45{}^\circ )$

Penyelesaian: Lihat/Tutup

Dari grafik dapat kita tentukan untuk sementara persamaannya adalah $y=A\sin (kx+b)$.
${{y}_{\text{maks}}}=2$ dan ${{y}_{\text{maks}}}=-2$
$\begin{align}A &=\frac{1}{2}\left( {{y}_{\text{maks}}}-{{y}_{\text{min}}} \right) \\ &=\frac{1}{2}\left( 2-(-2) \right) \\ A &=2 \end{align}$
Periode dari $15{}^\circ $ sampai $135{}^\circ $ maka:
$p=135{}^\circ -15{}^\circ =120{}^\circ $
Ingat periode fungsi sinus adalah:
$\begin{align}p &=\frac{360{}^\circ }{k} \\ 120{}^\circ &=\frac{360{}^\circ }{k} \\ k &=\frac{360{}^\circ }{120{}^\circ } \\ k &=3 \end{align}$
Grafik melalui titik $(45{}^\circ ,2)$ maka:
$\begin{align}y &=A\sin (kx+b) \\ 2 &=2.\sin (3.45{}^\circ +b) \\ 1 &=\sin (135{}^\circ +b) \\ sin90{}^\circ &=\sin (135{}^\circ +b) \\ 135{}^\circ +b &=90{}^\circ \\ b &=90{}^\circ -135{}^\circ \\ b &=-45{}^\circ \end{align}$
Jadi, persamaan grafik tersebut adalah $y=A\sin (kx+b)\Leftrightarrow y=2\sin (3x-45{}^\circ )$.
Jawaban: E

---

Soal No. 11

Nilai maksimum dari fungsi trigonometri $f(x)=\cos \left( 8x-\frac{\pi }{8} \right)-\frac{2}{3}$ adalah ….
(A) $-\frac{1}{3}$
(B) $-\frac{1}{8}$
(C) 0
(D) $\frac{1}{8}$
(E) $\frac{1}{3}$

Penyelesaian: Lihat/Tutup

Ingat bentuk umum fungsi trigonometri:
$f(x)=a\cos (kx+b)+c$ maka dari $f(x)=\cos \left( 8x-\frac{\pi }{8} \right)-\frac{2}{3}$ diperoleh:
$a=1$ dan $c=-\frac{2}{3}$ maka:
$\begin{align}{{f}_{\text{maks}}} &=|a|+c \\ &=|1|-\frac{2}{3} \\ {{f}_{\text{maks}}} &=\frac{1}{3} \end{align}$
Jawaban: E

---

Soal No. 12

Nilai minimum yang dapat dicapai oleh fungsi $f(x)=-2\cos x+1$ adalah …
(A) $-3$
(B) $-2$
(C) $-1$
(D) 2
(E) 3

Penyelesaian: Lihat/Tutup

Ingat bentuk umum fungsi trigonometri:
$f(x)=a\cos (kx+b)+c$ maka dari $f(x)=-2\cos x+1$ diperoleh:
$a=-2$ dan $c=1$ maka:
$\begin{align}{{f}_{\text{min}}} &=-|a|+c \\ &=-|-2|+1 \\ {{f}_{\text{min}}} &=-1 \end{align}$
Jawaban: C

---

Soal No. 13

Jika $f(x)=2-{{\sin }^{2}}x$, maka fungsi $f$ memenuhi ….
(A) $-2\le f(x)\le -1$
(B) $-2\le f(x)\le 1$
(C) $-1\le f(x)\le 0$
(D) $0\le f(x)\le 1$
(E) $1\le f(x)\le 2$

Penyelesaian: Lihat/Tutup

Nilai $f(x)=2-{{\sin }^{2}}x$ akan minimum, jika ${{\sin }^{2}}x$ maksimum yaitu ${{\sin }^{2}}x=1$ maka:
${{f}_{\text{min}}}=2-1=1$.
Nilai $f(x)=2-{{\sin }^{2}}x$ akan maksimum, jika ${{\sin }^{2}}x$ minimum yaitu ${{\sin }^{2}}x=0$ maka:
${{f}_{\text{maks}}}=2-0=2$.
Nilai interval fungsi f(x) adalah:
$\begin{align}{{f}_{\text{min}}}\le f(x) &\le {{f}_{\text{maks}}} \\ 1\le f(x) & \le 2 \end{align}$
Jawaban: E

---

Soal No. 14

Jika $f(x)=5\sin x+2$ mempunyai maksimum $a$ dan minimum $b$ maka nilai $ab$ = ….
(A) 0
(B) 3
(C) $-15$
(D) $-18$
(E) $-21$

Penyelesaian: Lihat/Tutup

Bentuk umum: $f(x)=A\sin (kx+B)+C$, maka dari $f(x)=5\sin x+2$ diperoleh:
$A=5$ dan $C=2$
$\begin{align}{{f}_{\text{maks}}} &=|A|+C \\ &=|5|+2 \\ a &=7 \end{align}$
$\begin{align}{{f}_{\text{min}}} &=-|A|+C \\ &=-|5|+2 \\ b &=-3 \end{align}$
$ab=7(-3)=-21$
Jawaban: E

---

Soal No. 15

Nilai minimum dari fungsi $f(x)=2\sin \left( x-\frac{\pi }{3} \right)+1$ adalah …
(A) $-2$
(B) $-1$
(C) 0
(D) 1
(E) 2

Penyelesaian: Lihat/Tutup

Ingat bentuk umum: $f(x)=A\sin (kx+b)+c$
Dari $f(x)=2\sin \left( x-\frac{\pi }{3} \right)+1$ diperoleh $A=2$ dan c = 1
$\begin{align}{{y}_{\min }} &=-|A|+c \\ &=-|2|+1 \\ {{y}_{\min }} &=-1 \end{align}$
Jawaban: B

---

Semoga postingan: Soal Grafik Fungsi Trigonometri dan Pembahasan ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :