Cara Menentukan Sistem Pertidaksamaan Linear Jika Daerah Himpunan Penyelesaian Diketahui

Menentukan Sistem Pertidaksamaan Linear Jika Daerah Himpunan Penyelesaian Diketahui

Contoh 1.

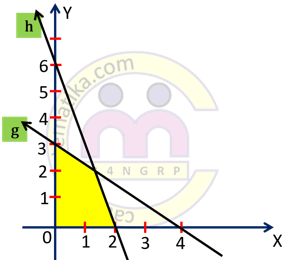
Sistem pertidaksamaan untuk daerah himpunan penyelesaian pada gambar di atas adalah ....
Penyelesaian:
1. Garis g melalui titik (0,3) dan (4, 0) maka persamaan garis g adalah:
$ax+by=ab$
$3x+4y=12$
Daerah penyelesaian di sebelah kiri garis g maka pertidaksamaannya adalah:
$3x+4y\le 12$
2. Garis h melalui titik (0,6) dan (2,0) maka persamaan garis h adalah:
$ax+by=ab$
$6x+2y=12$
Daerah penyelesaian di sebelah kiri garis h maka pertidaksamaannya adalah:
$6x+2y\le 12$ atau $3x+y\le 6$.
3. Daerah penyelesaian di sebelah kanan sumbu Y, maka: $x\ge 0$.
4. Daerah penyelesaian di sebelah atas sumbu X, maka: $y\ge 0$.
Jadi, sistem pertidaksamaan daerah penyelesaian pada gambar adalah:
$3x+4y\le 12$
$3x+y\le 6$
$x\ge 0$
$y\ge 0$

Contoh 2.

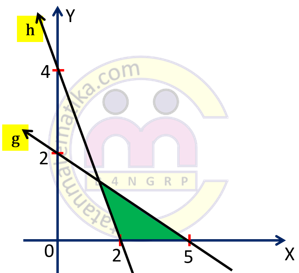
Sistem pertidaksamaan untuk daerah himpunan penyelesaian pada gambar di atas adalah ....
Penyelesaian:
1. Garis g melalui titik (0, 2) dan (5, 0) maka persamaan garis g adalah:
$ax+by=ab$
$2x+5y=10$
Daerah penyelesaian di sebelah kiri garis g maka pertidaksamaannya adalah:
$2x+5y\le 10$
2. Garis h melalui titik (0,4) dan (2,0) maka persamaan garis h adalah:
$ax+by=ab$
$4x+2y=8$
Daerah penyelesaian di sebelah kanan garis h maka pertidaksamaannya adalah:
$4x+2y\ge 8$ atau $2x+y\ge 4$
3. Daerah penyelesaian di sebelah kanan sumbu Y, maka: $x\ge 0$.
4. Daerah penyelesaian di sebelah atas sumbu X, maka $y\ge 0$
Jadi, sistem pertidaksamaan linear daerah penyelesaian pada gambar adalah:
$2x+5y\le 10$
$2x+y\ge 4$
$x\ge 0$
$y\ge 0$

Contoh 3.

Sistem pertidaksamaan untuk daerah himpunan penyelesaian pada gambar di atas adalah ...
Penyelesaian:
1. Garis g melalui titik (0,3) dan (5,0) maka persamaan garis g adalah:
$ax+by=ab$
$3x+5y=15$
Daerah penyelesaian di sebelah kanan garis g maka pertidaksamaannya adalah:
$3x+5y\ge 15$
2. Garis h melalui titik (0,5) dan (4,0) maka persamaan garis h adalah:
$ax+by=ab$
$5x+4y=20$
Daerah penyelesaian di sebelah kanan garis g maka pertidaksamaannya adalah:
$5x+4y\ge 20$
3. Daerah penyelesaian di sebelah kanan sumbu Y, maka $x\ge 0$.
4. Daerah penyelesaian di sebelah atas sumbu X, maka $y\ge 0$.
Jadi, sistem pertidaksamaan daerah penyelesaian pada gambar adalah:
$3x+5y\ge 15$
$5x+4y\ge 20$
$x\ge 0$
$y\ge 0$

Contoh 4.

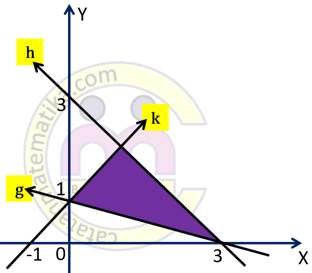
Sistem pertidaksamaan untuk daerah himpunan penyelesaian pada gambar di atas adalah:
Penyelesaian:
1. Garis g melalui titik (0,1) dan (3,0) maka persamaan garis g adalah:
$ax+by=ab$
$x+3y=3$
Daerah penyelesaian di sebelah kanan garis g maka pertidaksamaannya adalah:
$x+3y\ge 3$
2. Garis h melalui titik (0,3) dan (3,0) maka persamaan garis h adalah:
$ax+by=ab$
$3x+3y=9$
Daerah penyelesaian di sebelah kiri garis h maka pertidaksamaannya adalah:
$3x+3y\le 9$ atau $x+y\le 3$
3. Garis k melalui titik (0,1) dan (-1,0) maka persamaan garis k adalah:
$ax+by=ab$
$x-y=-1$
Daerah penyelesaian di sebelah kanan garis k maka pertidaksamaannya adalah:
$x-y\ge -1$
Jadi, sistem pertidaksamaan daerah penyelesaian pada gambar adalah:
$x+3y\ge 3$
$x+y\le 3$
$x-y\ge -1$

Contoh 5.

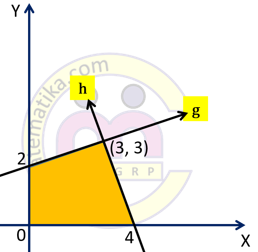
Sistem pertidaksamaan untuk daerah himpunan penyelesaian pada gambar di atas adalah ...
Penyelesaian:
1. Garis g melalui titik (0,2) dan (3,3) maka persamaan garis g adalah:
$\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$
$\frac{y-2}{3-2}=\frac{x-0}{3-0}$
$\frac{y-2}{1}=\frac{x}{3}$
$x=3(y-2)$
$x=3y-6$
$x-3y+6=0$
Daerah penyelesaian di sebelah kanan garis g, maka pertidaksamaannya adalah:
$x-3y+6\ge 0$.
2. Garis h melalui titik (3,3) dan (4,0) maka persamaan garis h adalah:
$\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$
$\frac{y-3}{0-3}=\frac{x-3}{4-3}$
$\frac{y-3}{-3}=\frac{x-3}{1}$
$y-3=-3(x-3)$
$y-3=-3x+9$
$3x+y-12=0$
Daerah penyelesaian di sebelah kiri garis h, maka pertidaksamaannya adalah:
$3x+y-12\le 0$
3. Daerah penyelesaian di sebelah kanan sumbu Y, maka $x\ge 0$.
4. Daerah penyelesaian di sebelah kiri sumbu X, maka $y\ge 0$.

LATIHAN

---

Soal No. 1

Tentukan sistem pertidaksamaan linear dari daerah himpunan penyelesaian pada gambar di atas.
Soal No. 2

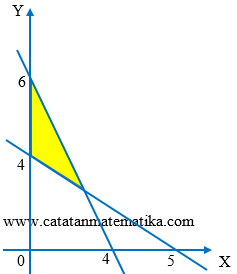
Tentukan sistem pertidaksamaan linear dari daerah himpunan penyelesaian pada gambar di atas.

Semoga postingan: Cara Menentukan Sistem Pertidaksamaan Linear Jika Daerah Himpunan Penyelesaian Diketahui ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :