Perbandingan Trigonometri pada Segitiga Siku-siku

A. Mengenal Jenis-jenis Sisi pada Segitiga Siku-siku

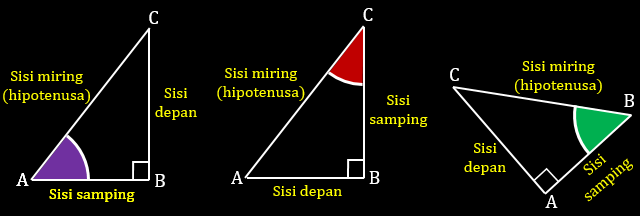
Pada segitiga siku-siku terdapat tiga jenis sisi. Berdasarkan posisinya terhadap sudut tertentu, kita dapat menamai ketiga sisi tersebut dengan:

1. Sisi depan, yaitu sisi siku-siku yang berada di depan sudut.
2. Sisi samping, yaitu sisi siku-siku yang berada di samping sudut.
3. Sisi miring (hipotenusa), yaitu sisi yang berada di depan sudut siku-siku.

Untuk lebih memahaminya lukislah segitiga ABC dengan sudut siku-siku terletak di titik A. Berdasarkan sudut B maka dapat kita tentukan jenis-jenis sisi sebagai seperti pada gambar berikut.

Supaya semakin memahami, coba perhatikan gambar-gambar berikut ini! Pada gambar diberi tanda pada satu sudut, kemudian jenis-jenis sisi pada setiap sisi segitiga.

B. Perbandingan Trigonometri pada Segitiga Siku-siku

Perbandingan trigonometri ada 6 yaitu:
1. Sinus disingkat sin.
2. Cosinus disingkat cos.
3. Tangen disingkat tan.
4. Cosecan disingkat csc.
5. Secan disingkat sec.
6.Cotangen disingkat cot.

Definisi Perbandingan Trigonometri

Perhatikan gambar berikut!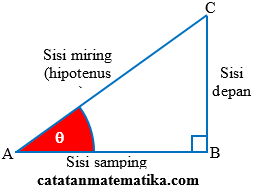

1. $\sin \theta =\frac{\text{sisi}\,\text{depan}}{\text{sisi}\,\text{miring}}=\frac{BC}{AC}$
2. $\cos \theta =\frac{\text{sisi samping}}{\text{sisi}\,\text{miring}}=\frac{AB}{AC}$
3. $\tan \theta =\frac{\text{sisi depan}}{\text{sisi samping}}=\frac{BC}{AB}$
4. $\csc \theta =\frac{\text{sisi miring}}{\text{sisi depan}}=\frac{AC}{BC}$
5. $\sec \theta =\frac{\text{sisi miring}}{\text{sisi samping}}=\frac{AC}{AB}$
6. $\cot \theta =\frac{\text{sisi samping}}{\text{sisi depan}}=\frac{AB}{BC}$
Cara mudah menghafal rumus perbandingan trigonometri:
1. $\sin \theta =\frac{\text{de}}{\text{mi}}$, baca “sindemi”
2. $\cos \theta =\frac{\text{sa}}{\text{mi}}$, baca “cosami”
3. $\tan \theta =\frac{\text{de}}{\text{sa}}$, baca “tadesa”

C. Rumus Kebalikan dan Rumus Perbandingan

Perhatikan gambar berikut!

Teorema phythagoras:
$r=\sqrt{x^2+y^2}$
$x=\sqrt{r^2-y^2}$
$y=\sqrt{r^2-x^2}$
Perbandingan trigonometri: $\sin \theta =\frac{y}{r}$ dan $\csc \theta =\frac{r}{y}$
$\cos \theta =\frac{x}{r}$ dan $\sec \theta =\frac{r}{x}$
$\tan \theta =\frac{y}{x}$ dan $\cot \theta =\frac{x}{y}$
Dari perbandingan trigonometri tersebut dapat diturunkan rumus-rumus sebagai berikut:

Rumus Kebalikan
a) $\sin \theta =\frac{1}{\csc \theta }\Leftrightarrow \csc \theta =\frac{1}{\sin \theta }$
b) $\cos \theta =\frac{1}{\sec \theta }\Leftrightarrow \sec \theta =\frac{1}{\cos \theta }$
c) $\tan \theta =\frac{1}{\cot \theta }\Leftrightarrow \cot \theta =\frac{1}{\tan \theta }$
Rumus Perbandingan
a) $\tan \theta =\frac{\sin \theta }{\cos \theta }$
b) $\cot \theta =\frac{\cos \theta }{\sin \theta }$

Contoh 1.

Perhatikan gambar berikut!

Tentukan nilai keenam perbandingan trigonometri untuk sudut $\beta $.

Penyelesaian: Lihat/Tutup

Dengan Teorema Pythagoras:
$\begin{align}AB &=\sqrt{AC^2-BC^2} \\ &=\sqrt{4^2-3^2} \\ &=\sqrt{16-9} \\ AB &=\sqrt{7} \end{align}$
Berdasarkan sudut $\beta $ maka:
Sisi depan = AB = $\sqrt{7}$
Sisi samping = BC = 3
Sisi miring = AC = 4
$\sin \beta =\frac{de}{mi}=\frac{\sqrt{7}}{4}$
$\cos \beta =\frac{sa}{mi}=\frac{3}{4}$
$\tan \beta =\frac{de}{sa}=\frac{\sqrt{7}}{3}$
$\csc \beta =\frac{mi}{de}=\frac{4}{\sqrt{7}}=\frac{4}{7}\sqrt{7}$
$\sec \beta =\frac{mi}{sa}=\frac{4}{3}$
$\cot \beta =\frac{sa}{de}=\frac{3}{\sqrt{7}}=\frac{3}{7}\sqrt{7}$

---

Contoh 2.

Diketahui nilai $\tan \alpha =\frac{1}{3}$ untuk $0^\circ < \alpha < 90^\circ $. Carilah nilai perbandingan trigonometri sudut $\alpha $ yang lain.

Penyelesaian: Lihat/Tutup

$\tan \alpha =\frac{1}{3}=\frac{de}{sa}$
Kemudian gambar segitiga siku-siku sesuai perbandingan tersebut.

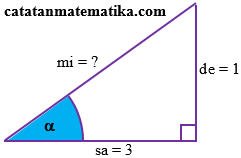
$\begin{align}mi &=\sqrt{sa^2+de^2} \\ &=\sqrt{3^2+1^2} \\ &=\sqrt{9+1} \\ mi &=\sqrt{10} \end{align}$
$\sin \beta =\frac{de}{mi}=\frac{1}{\sqrt{10}}=\frac{1}{10}\sqrt{10}$
$\cos \beta =\frac{sa}{mi}=\frac{3}{\sqrt{10}}=\frac{3}{10}\sqrt{10}$
$\tan \beta =\frac{de}{sa}=\frac{1}{3}$
$\csc \beta =\frac{mi}{de}=\sqrt{10}$
$\sec \beta =\frac{mi}{sa}=\frac{\sqrt{10}}{3}$
$\cot \beta =\frac{sa}{de}=\frac{3}{1}=3$

---

Contoh 3.

Diketahui nilai $\sin 25{}^\circ =p$, maka nilai $\tan 25^\circ $ = ...

Penyelesaian: Lihat/Tutup

$\sin 25^\circ =p=\frac{p}{1}=\frac{de}{mi}$
Kemudian gambar segitiga siku-siku sesuai dengan perbandingan tersebut.

$\begin{align}sa &=\sqrt{mi^2-de^2} \\ &=\sqrt{1^2-p^2} \\ sa &=\sqrt{1-p^2} \end{align}$
$\tan 25^\circ =\frac{de}{sa}=\frac{p}{\sqrt{1-p^2}}$

---

Contoh 4.

Diketahui nilai $\cos A=0,6$. Jika sudut A adalah sudut lancip, maka $2\sin A\tan A$ = ...

Penyelesaian: Lihat/Tutup

$\cos A=0,6=\frac{6}{10}=\frac{sa}{mi}$
Gambar segitiga siku-siku sesuai dengan perbandingan tersebut.

$\begin{align}de &=\sqrt{mi^2-sa^2} \\ &=\sqrt{10^2-6^2} \\ &=\sqrt{100-36} \\ &=\sqrt{64} \\ de &=8 \end{align}$
$\sin A=\frac{de}{mi}=\frac{8}{10}=\frac{4}{5}$
$\tan A=\frac{de}{sa}=\frac{8}{6}=\frac{4}{3}$
$2\sin A\tan A=2.\frac{4}{5}.\frac{4}{3}=\frac{32}{15}$

---

Contoh 5.

Diketahui nilai $\cos A=0,6$. Jika sudut A adalah sudut lancip, maka $2\sin A\tan A$ = ...

Penyelesaian: Lihat/Tutup

$\cos A=0,6=\frac{6}{10}=\frac{sa}{mi}$
Gambar segitiga siku-siku sesuai dengan perbandingan tersebut.
Gambar 8.
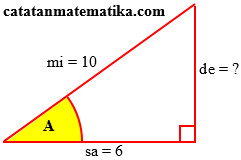
$\begin{align}de &=\sqrt{mi^2-sa^2} \\ &=\sqrt{10^2-6^2} \\ &=\sqrt{100-36} \\ &=\sqrt{64} \\ de &=8 \end{align}$
$\sin A=\frac{de}{mi}=\frac{8}{10}=\frac{4}{5}$
$\tan A=\frac{de}{sa}=\frac{8}{6}=\frac{4}{3}$
$2\sin A\tan A=2.\frac{4}{5}.\frac{4}{3}=\frac{32}{15}$

---

D. Soal Latihan

1. Diketahui segitiga ABC, siku-siku di titik C. Jika panjang AC = 24 cm, BC = 7 cm, dan $\angle BAC=\alpha $, maka tentukan nilai keenam perbandingan trigonometri untuk sudut $\alpha $.
2. Jika diketahui $\cos \theta =\frac{1}{k}$ untuk $0^\circ < \theta < 90^\circ $ maka $\tan \theta $ = ...
3. Diketahui sudut A adalah sudut lancip. Jika $\tan A=\frac{12}{5}$ maka $\sin A+\cos A$ = ...
4. Diketahui $0^\circ < B < 90^\circ $. Jika $\cos B=\frac{2}{3}$ maka ${{\sin }^{2}}A-{{\tan }^{2}}A$ = ....

Semoga postingan: Perbandingan Trigonometri pada Segitiga Siku-siku ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :