Perbandingan Trigonometri di Berbagai Kuadran

A. Pembagian Sudut dalam Trigonometri

Dalam trignometri, besar suatu sudut $\alpha $ dibagi ke dalam 4 kuadran, yaitu:

• Kuadran I ($0^\circ < \alpha < 90^\circ $)
• Kuadran II ($90^\circ < \alpha < 180^\circ $)
• Kuadran III ($180^\circ < \alpha < 270^\circ $).
• Kuadran IV ($270^\circ < \alpha < 360^\circ $).

Perhatikan gambar berikut!

B. Menentukan Nilai Perbandingan Trigonometri di Berbagai Kuadran

Perhatikan gambar berikut!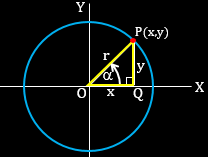

$\alpha $ adalah sudut yang dibentuk oleh garis OP dan sumbu X positif di titik O(0,0).
Perbandingan trigonometri:
Diketahui titik P(x,y), $\alpha $ adalah sudut yang dibentuk oleh garis OP (panjangnya r) dan sumbu X positif di titik O(0,0), maka:
$\sin \alpha =\frac{PQ}{OP}\Rightarrow \sin \alpha =\frac{y}{r}\Leftrightarrow \csc \alpha =\frac{r}{y}$
$\cos \alpha =\frac{OQ}{OP}\Rightarrow \cos \alpha =\frac{x}{r}\Leftrightarrow \sec \alpha =\frac{r}{x}$
$\tan \alpha =\frac{PQ}{OQ}\Rightarrow \tan \alpha =\frac{y}{x}\Leftrightarrow \csc \alpha =\frac{x}{y}$

1. Nilai Perbandingan Trigonometri di Kuadran I

Perhatikan gambar berikut!

Dari titik $(a,b)$ diperoleh $x=a$, $y=b$
Perbandingan trigonometri:
$\sin \alpha =\frac{y}{r}=\frac{b}{r}(positif)$
$\cos \alpha =\frac{x}{r}=\frac{a}{r}(positif)$
$\tan \alpha =\frac{y}{x}=\frac{b}{a}(positif)$
$\csc \alpha =\frac{r}{y}=\frac{r}{b}(positif)$
$\sec \alpha =\frac{r}{x}=\frac{r}{a}(positif)$
$\cot \alpha =\frac{x}{y}=\frac{a}{b}(positif)$

Jadi, nilai perbandingan trigonometri sudut di kuadran I semuanya positif.

2. Nilai Perbandingan Trigonometri di Kuadran II

Perhatikan gambar berikut!

Dari Titik $(-a,b)$ diperoleh $x=-a$ dan $y=b$
Perbandingan trigonometri:
$\sin \alpha =\frac{y}{r}=\frac{b}{r}(positif)$
$\cos \alpha =\frac{x}{r}=\frac{-a}{r}(negatif)$
$\tan \alpha =\frac{y}{x}=\frac{b}{-a}(negatif)$
$\csc \alpha =\frac{r}{y}=\frac{r}{b}(positif)$
$\sec \alpha =\frac{r}{x}=\frac{r}{-a}(negatif)$
$\cot \alpha =\frac{x}{y}=\frac{-a}{b}(negatif)$

Jadi, nilai perbandingan trigonometri sudut di kuadran II, sinus dan cosecan positif.

3. Nilai Perbandingan Trigonometri di Kuadran III

Perhatikan gambar berikut!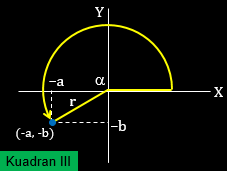

Dari titik $(-a,-b)$ maka $x=-a$ dan $y=-b$
Perbandingan Trigonometri:
$\sin \alpha =\frac{y}{r}=\frac{-b}{r}(negatif)$
$\cos \alpha =\frac{x}{r}=\frac{-a}{r}(negatif)$
$\tan \alpha =\frac{y}{x}=\frac{-b}{-a}=\frac{a}{b}(positif)$
$\csc \alpha =\frac{r}{y}=\frac{r}{-b}(negatif)$
$\sec \alpha =\frac{r}{x}=\frac{r}{-a}(negatif)$
$\cot \alpha =\frac{x}{y}=\frac{-a}{-b}=\frac{a}{b}(positif)$

Jadi, nilai perbandingan trigonometri sudut di kuadran III, tangen dan cotangen positif.

4. Nilai Perbandingan Trigonometri di Kuadran IV

Perhatikan gambar berikut!

Dari titik $(a,-b)$ maka $x=a$ dan $y=-b$
Perbandingan Trigonometri:
$\sin \alpha =\frac{y}{r}=\frac{-b}{r}(negatif)$
$\cos \alpha =\frac{x}{r}=\frac{a}{r}(positif)$
$\tan \alpha =\frac{y}{x}=\frac{-b}{a}(negatif)$
$\csc \alpha =\frac{r}{y}=\frac{r}{-b}(negatif)$
$\sec \alpha =\frac{r}{x}=\frac{r}{a}(positif)$
$\cot \alpha =\frac{x}{y}=\frac{a}{-b}(negatif)$

Jadi, nilai perbandingan trigonometri sudut di kuadran IV, cosinus dan secan positif.

Kesimpulan: Nilai Perbandingan Trigonometri di Berbagai Kuadran

Contoh Soal dan Pembahasan

Contoh 1.

Diketahui $\alpha $ adalah sudut lancip dan $\sin \alpha =\frac{12}{13}$, maka $\tan \alpha +\cos \alpha $ = ...
Penyelesaian:
$\sin \alpha =\frac{12}{13}=\frac{de}{mi}$
Gambar segitiga siku-siku sesuai perbandingan tersebut.

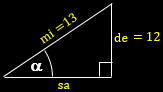
Teorema pythagoras:
$\begin{align}sa &=\sqrt{mi^2-de^2} \\ &=\sqrt{13^2-12^2} \\ &=\sqrt{169-144} \\ &=\sqrt{25} \\ sa &=5 \end{align}$
$\alpha $ adalah sudut lancip (kuadran I) maka semua perbandingan trigonometri bernilai positif.
$\tan \alpha =\frac{de}{sa}=\frac{12}{5}$
$\cos \alpha =\frac{sa}{mi}=\frac{5}{13}$
maka:
$\tan \alpha +\cos \alpha =\frac{12}{5}+\frac{5}{13}=\frac{181}{65}$

Contoh 2.

Diketahui $\beta $ adalah sudut tumpul dan $\cos \beta =-\frac{4}{5}$, maka $\sin \beta .\tan \beta $ = ...
Penyelesaian:
$\cos \beta =-\frac{4}{5}=\frac{sa}{mi}$
Gambar segitiga sesuai perbandingan tersebut, “abaikan” tanda negatif.

Teorema pythagoras:
$\begin{align}de &=\sqrt{mi^2-sa^2} \\ &=\sqrt{5^2-4^2} \\ &=\sqrt{25-16} \\ &=\sqrt{9} \\ de &=3 \end{align}$
$\beta $ adalah sudut tumpul (kuadran II) maka $\sin \beta (+)$ dan $\csc \beta (+)$.
$\sin \beta =\frac{de}{mi}=\frac{3}{5}$
$\tan \beta =-\frac{de}{sa}=-\frac{3}{4}$
maka:
$\sin \beta \times \tan \beta =\frac{3}{5}\times \left( -\frac{3}{4} \right)=-\frac{9}{20}$

Contoh 3.

Diketahui $270^\circ < A < 360 ^\circ $ dan $\tan A=-2,4$ maka $\sin A$ = ...
Penyelesaian:
$\begin{align}\tan A &= -2,4 \\ &= -\frac{24}{10} \\ \tan A &= -\frac{12}{5}=\frac{de}{sa} \end{align}$
Gambar segitiga siku-siku sesuai perbandingan tersebut, “abaikan” tanda negatif.

Teorema pythagoras:
$\begin{align}mi &=\sqrt{de^2+sa^2} \\ &=\sqrt{12^2+5^2} \\ &=\sqrt{144+25} \\ &=\sqrt{169} \\ mi &=13 \end{align}$
$270^\circ < A < 360^\circ $ (Kuadran IV), maka $\cos A(+)$ dan $\sec A(+)$
maka:
$\sin A=-\frac{de}{mi}=-\frac{12}{13}$

Contoh 4.

Jika $\sec \beta =-3$, dengan $\pi < \beta < \frac{3\pi }{2}$ maka $\sin \beta $ = ...
Penyelesaian:
$\sec \beta =-3$
$\cos \beta =\frac{1}{\sec \beta }=-\frac{1}{3}=\frac{sa}{mi}$
Gambar segitiga siku-siku sesuai perbandingan tersebut, “abaikan” tanda negatif.

Teorema pythagoras:
$\begin{align}de &=\sqrt{mi^2-sa^2} \\ &=\sqrt{3^2-1^2} \\ &=\sqrt{9-1} \\ &=\sqrt{8} \\ de &=2\sqrt{2} \end{align}$
$\pi < \beta < \frac{3\pi }{2}$ (kuadran III) maka $\tan \beta (+)$ dan $\cot \beta (+)$
maka:
$\sin \beta =-\frac{de}{mi}=-\frac{2\sqrt{2}}{3}$

Contoh 5.

Diketahui $\sin A=\frac{3}{5}$ dan $\tan B=\frac{7}{24}$, jika A sudut tumpul dan B sudut lancip maka $\cos A.\sin B$ = ...
Penyelesaian:
Sudut A:
$\sin A=\frac{3}{5}=\frac{de}{mi}$

Teorema pythagoras:
$\begin{align}sa &=\sqrt{mi^2-de^2} \\ &=\sqrt{5^2-3^2} \\ &=\sqrt{25-9} \\ &=\sqrt{16} \\ sa &=4 \end{align}$
A sudut tumpul (kuadran II), maka $\sin A(+)$ dan $\csc A(+)$
maka:
$\cos A=-\frac{sa}{mi}=-\frac{4}{5}$
Sudut B:
$\tan B=\frac{7}{24}=\frac{de}{sa}$

$\begin{align}mi &=\sqrt{de^2+sa^2} \\ &=\sqrt{7^2+24^2} \\ &=\sqrt{49+576} \\ &=\sqrt{625} \\ sa &=25 \end{align}$
B sudut lancip (kuadran I), nilai perbandingan trigonometri semua positif, maka:
$\sin B=\frac{de}{mi}=\frac{7}{25}$
$\cos A.\sin B=-\frac{4}{5}\times \frac{7}{25}=-\frac{28}{125}$

Soal Latihan

1. Jika $\tan \alpha =\frac{8}{15}$; dengan $\alpha $ sudut di kuadran III, maka $\cos \alpha $ = ...
2. Jika $\cos \beta =-\frac{1}{4}$, dengan $\beta $ sudut di kuadran II, maka $\sin \beta $ = ...
3. Jika $\cot A=-\frac{12}{5}$, dengan A sudut di kuadran IV, maka $\sec A$ = ...
4. Jika $\sin \alpha =\frac{2\sqrt{5}}{5}$, dengan $\alpha $ sudut di kuadran I, maka $\tan \alpha $ = ...
5. Jika $\cos \alpha =-\frac{24}{25}$, $\tan \beta =\frac{9}{40}$, $\frac{\pi }{2} < \alpha < \pi $, dan $\pi < \beta < \frac{3\pi }{2}$ maka $\sin \alpha .\cos \beta $ = ...

by: Catatan Matematika

Semoga postingan: Perbandingan Trigonometri di Berbagai Kuadran ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :