Perbandingan Trigonometri Sudut Berelasi

A. Sudut Berelasi di Kuadran I

1. Relasi sudut $\alpha $ dan $(360^\circ +\alpha )$

Perhatikan gambar berikut:

Titik $P(a,b)$ dan sudut $\alpha $, maka:
$\sin \alpha =\frac{y}{r}\Leftrightarrow \sin \alpha =\frac{b}{r}$
$\cos \alpha =\frac{x}{r}\Leftrightarrow \cos \alpha =\frac{a}{r}$
$\tan \alpha =\frac{y}{x}\Leftrightarrow \tan \alpha =\frac{b}{a}$
$\cot \alpha =\frac{x}{y}\Leftrightarrow \cot \alpha =\frac{a}{b}$
Titik $P'(a,b)$ dan sudut $(360^\circ +\alpha )$, maka:
$\sin (360^\circ +\alpha )=\frac{y}{r}\Leftrightarrow \sin (360^\circ +\alpha )=\frac{b}{r}$
$\cos (360^\circ +\alpha )=\frac{x}{r}\Leftrightarrow \cos (360^\circ +\alpha )=\frac{a}{r}$
$\tan (360^\circ +\alpha )=\frac{y}{x}\Leftrightarrow \tan (360^\circ +\alpha )=\frac{b}{a}$

Kesimpulan:
$\sin (360^\circ +\alpha )=\sin \alpha $
$\cos (360^\circ +\alpha )=\cos \alpha $
$\tan (360^\circ +\alpha )=\tan \alpha $

2. Relasi sudut $\alpha $ dan $(90^\circ -\alpha )$

Perhatikan gambar berikut:

Titik $P(a,b)$ dan sudut $\alpha $, maka:
$\sin \alpha =\frac{y}{r}\Leftrightarrow \sin \alpha =\frac{b}{r}$
$\cos \alpha =\frac{x}{r}\Leftrightarrow \cos \alpha =\frac{a}{r}$
$\tan \alpha =\frac{y}{x}\Leftrightarrow \tan \alpha =\frac{b}{a}$
$\cot \alpha =\frac{x}{y}\Leftrightarrow \cot \alpha =\frac{a}{b}$
Titik $P'(a,b)$ dan sudut $(90^\circ -\alpha )$, maka:
$\sin (90^\circ -\alpha )=\frac{y}{r}\Leftrightarrow \sin (90^\circ -\alpha )=\frac{a}{r}$
$\cos (90^\circ -\alpha )=\frac{x}{r}\Leftrightarrow \cos (90^\circ -\alpha )=\frac{b}{r}$
$\tan (90^\circ -\alpha )=\frac{y}{x}\Leftrightarrow \tan (90^\circ -\alpha )=\frac{a}{b}$

Kesimpulan:
$\sin (90^\circ -\alpha )=\cos \alpha $
$\cos (90^\circ -\alpha )=\sin \alpha $
$\tan (90^\circ -\alpha )=\cot \alpha $

B. Sudut Berelasi di Kuadran II

1. Relasi sudut $\alpha $ dan $(90^\circ +\alpha )$

Perhatikan gambar berikut: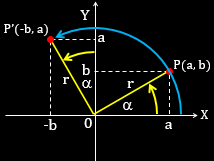

Titik $P(a,b)$ dan sudut $\alpha $, maka:
$\sin \alpha =\frac{y}{r}\Leftrightarrow \sin \alpha =\frac{b}{r}$
$\cos \alpha =\frac{x}{r}\Leftrightarrow \cos \alpha =\frac{a}{r}$
$\tan \alpha =\frac{y}{x}\Leftrightarrow \tan \alpha =\frac{b}{a}$
$\cot \alpha =\frac{x}{y}\Leftrightarrow \cot \alpha =\frac{a}{b}$
Titik $P'(-b,a)$ dan sudut $(90^\circ +\alpha )$, maka:
$\sin (90^\circ +\alpha )=\frac{y}{r}\Leftrightarrow \sin (90^\circ +\alpha )=\frac{a}{r}$
$\cos (90^\circ +\alpha )=\frac{x}{r}\Leftrightarrow \cos (90^\circ +\alpha )=\frac{-b}{r}$
$\tan (90^\circ +\alpha )=\frac{y}{x}\Leftrightarrow \tan (90^\circ +\alpha )=\frac{a}{-b}$

Kesimpulan:
$\sin (90^\circ +\alpha )=\cos \alpha $
$\cos (90^\circ +\alpha )=-\sin \alpha $
$\tan (90^\circ -\alpha )=-\cot \alpha $

2. Relasi sudut $\alpha $ dan $(180^\circ -\alpha )$

Perhatikan gambar berikut: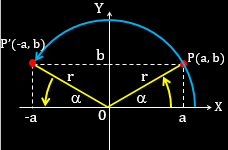

Titik $P(a,b)$ dan sudut $\alpha $, maka:
$\sin \alpha =\frac{y}{r}\Leftrightarrow \sin \alpha =\frac{b}{r}$
$\cos \alpha =\frac{x}{r}\Leftrightarrow \cos \alpha =\frac{a}{r}$
$\tan \alpha =\frac{y}{x}\Leftrightarrow \tan \alpha =\frac{b}{a}$
$\cot \alpha =\frac{x}{y}\Leftrightarrow \cot \alpha =\frac{a}{b}$
Titik $P'(-a,b)$ dan sudut $(180^\circ -\alpha )$, maka:
$\sin (180^\circ -\alpha )=\frac{y}{r}\Leftrightarrow \sin (180^\circ -\alpha )=\frac{b}{r}$
$\cos (180^\circ -\alpha )=\frac{x}{r}\Leftrightarrow \cos (180^\circ -\alpha )=\frac{-a}{r}$
$\tan (180^\circ -\alpha )=\frac{y}{x}\Leftrightarrow \tan (180^\circ -\alpha )=\frac{b}{-a}$

Kesimpulan:
$\sin (180^\circ -\alpha )=\sin \alpha $
$\cos (180^\circ -\alpha )=-\cos \alpha $
$\tan (180^\circ -\alpha )=-\tan \alpha $

C. Sudut Berelasi di Kuadran III

1. Relasi sudut $\alpha $ dan $(180^\circ +\alpha )$

Perhatikan gambar berikut: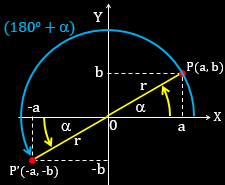

Titik $P(a,b)$ dan sudut $\alpha $, maka:
$\sin \alpha =\frac{y}{r}\Leftrightarrow \sin \alpha =\frac{b}{r}$
$\cos \alpha =\frac{x}{r}\Leftrightarrow \cos \alpha =\frac{a}{r}$
$\tan \alpha =\frac{y}{x}\Leftrightarrow \tan \alpha =\frac{b}{a}$
$\cot \alpha =\frac{x}{y}\Leftrightarrow \cot \alpha =\frac{a}{b}$
Titik $P'(-a,-b)$ dan sudut $(180^\circ +\alpha )$, maka:
$\sin (180^\circ +\alpha )=\frac{y}{r}\Leftrightarrow \sin (180^\circ +\alpha )=\frac{-b}{r}$
$\cos (180^\circ +\alpha )=\frac{x}{r}\Leftrightarrow \cos (180^\circ +\alpha )=\frac{-a}{r}$
$\tan (180^\circ +\alpha )=\frac{y}{x}\Leftrightarrow \tan (180^\circ +\alpha )=\frac{-b}{-a}=\frac{b}{a}$

Kesimpulan:
$\sin (180^\circ +\alpha )=-\sin \alpha $
$\cos (180^\circ +\alpha )=-\cos \alpha $
$\tan (180^\circ +\alpha )=\tan \alpha $

2. Relasi sudut $\alpha $ dan $(270^\circ -\alpha )$

Perhatikan gambar berikut!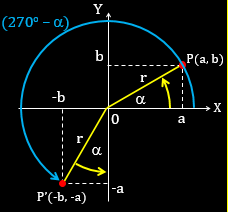

Titik $P(a,b)$ dan sudut $\alpha $, maka:
$\sin \alpha =\frac{y}{r}\Leftrightarrow \sin \alpha =\frac{b}{r}$
$\cos \alpha =\frac{x}{r}\Leftrightarrow \cos \alpha =\frac{a}{r}$
$\tan \alpha =\frac{y}{x}\Leftrightarrow \tan \alpha =\frac{b}{a}$
$\cot \alpha =\frac{x}{y}\Leftrightarrow \cot \alpha =\frac{a}{b}$
Titik $P'(-b,-a)$ dan sudut $(270^\circ -\alpha )$, maka:
$\sin (270^\circ -\alpha )=\frac{y}{r}\Leftrightarrow \sin (270^\circ -\alpha )=\frac{-a}{r}$
$\cos (270^\circ -\alpha )=\frac{x}{r}\Leftrightarrow \cos (270^\circ -\alpha )=\frac{-b}{r}$
$\tan (270^\circ -\alpha )=\frac{y}{x}\Leftrightarrow \tan (270^\circ -\alpha )=\frac{-a}{-b}=\frac{a}{b}$

Kesimpulan:
$\sin (270^\circ -\alpha )=-\cos \alpha $
$\cos (270^\circ -\alpha )=-\sin \alpha $
$\tan (270^\circ -\alpha )=\cot \alpha $

D. Sudut Berelasi di Kuadran IV

1. Relasi sudut $\alpha $ dan $(270^\circ +\alpha )$

Perhatikan gambar berikut!

Titik $P(a,b)$ dan sudut $\alpha $, maka:
$\sin \alpha =\frac{y}{r}\Leftrightarrow \sin \alpha =\frac{b}{r}$
$\cos \alpha =\frac{x}{r}\Leftrightarrow \cos \alpha =\frac{a}{r}$
$\tan \alpha =\frac{y}{x}\Leftrightarrow \tan \alpha =\frac{b}{a}$
$\cot \alpha =\frac{x}{y}\Leftrightarrow \cot \alpha =\frac{a}{b}$
Titik $P'(b,-a)$ dan sudut $(270^\circ +\alpha )$, maka:
$\sin (270^\circ +\alpha )=\frac{y}{r}\Leftrightarrow \sin (270^\circ +\alpha )=\frac{-a}{r}$
$\cos (270^\circ +\alpha )=\frac{x}{r}\Leftrightarrow \cos (270^\circ +\alpha )=\frac{b}{r}$
$\tan (270^\circ +\alpha )=\frac{y}{x}\Leftrightarrow \tan (270^\circ +\alpha )=\frac{-a}{b}$

Kesimpulan:
$\sin (270^\circ +\alpha )=-\cos \alpha $
$\cos (270^\circ +\alpha )=\sin \alpha $
$\tan (270^\circ +\alpha )=-\cot \alpha $

2. Relasi sudut $\alpha $ dan $(360^\circ -\alpha )$

Perhatikan gambar berikut!

Titik $P(a,b)$ dan sudut $\alpha $, maka:
$\sin \alpha =\frac{y}{r}\Leftrightarrow \sin \alpha =\frac{b}{r}$
$\cos \alpha =\frac{x}{r}\Leftrightarrow \cos \alpha =\frac{a}{r}$
$\tan \alpha =\frac{y}{x}\Leftrightarrow \tan \alpha =\frac{b}{a}$
$\cot \alpha =\frac{x}{y}\Leftrightarrow \cot \alpha =\frac{a}{b}$
Titik $P'(a,-b)$ dan sudut $(360^\circ -\alpha )$, maka:
$\sin (360^\circ -\alpha )=\frac{y}{r}\Leftrightarrow \sin (360^\circ -\alpha )=\frac{-b}{r}$
$\cos (360^\circ -\alpha )=\frac{x}{r}\Leftrightarrow \cos (360^\circ -\alpha )=\frac{a}{r}$
$\tan (360^\circ -\alpha )=\frac{y}{x}\Leftrightarrow \tan (360^\circ -\alpha )=\frac{-b}{a}$

Kesimpulan:
$\sin (360^\circ -\alpha )=-\sin \alpha $
$\cos (360^\circ -\alpha )=\cos \alpha $
$\tan (360^\circ -\alpha )=-\tan \alpha $

E. Perbandingan Trigonometri Sudut Negatif

Relasi Sudut $\alpha $ dengan $(-\alpha )$

Perhatikan gambar berikut!

Titik $P(a,b)$ dan sudut $\alpha $, maka:
$\sin \alpha =\frac{y}{r}\Leftrightarrow \sin \alpha =\frac{b}{r}$
$\cos \alpha =\frac{x}{r}\Leftrightarrow \cos \alpha =\frac{a}{r}$
$\tan \alpha =\frac{y}{x}\Leftrightarrow \tan \alpha =\frac{b}{a}$
$\cot \alpha =\frac{x}{y}\Leftrightarrow \cot \alpha =\frac{a}{b}$
Titik $P'(a,-b)$ dan sudut $(-\alpha )$, maka:
$\sin (-\alpha )=\frac{y}{r}\Leftrightarrow \sin (-\alpha )=\frac{-b}{r}$
$\cos (-\alpha )=\frac{x}{r}\Leftrightarrow \cos (-\alpha )=\frac{a}{r}$
$\tan (-\alpha )=\frac{y}{x}\Leftrightarrow \tan (-\alpha )=\frac{-b}{a}$

Kesimpulan:
$\sin (-\alpha )=-\sin \alpha $
$\cos (-\alpha )=\cos \alpha $
$\tan (-\alpha )=-\tan \alpha $

F. Contoh Soal dan Pembahasan

Contoh 1.

Nilai dari $\cos 35{}^\circ =m$ maka $\csc 55^\circ $ = ...
Penyelesaian:
$\begin{align}\csc 55^\circ &=\frac{1}{\sin 55^\circ } \\ &=\frac{1}{\sin (90^\circ -35^\circ )} \\ &=\frac{1}{\cos 35^\circ } \\ \csc 55^\circ &=\frac{1}{m} \end{align}$

Contoh 2.

Nilai dari $\tan \frac{5}{6}\pi $ = ....
Penyelesaian:
Cara 1.
$\begin{align}\tan \frac{5}{6}\pi &=\tan \frac{5}{6}\times 180^\circ \\ &=\tan 150^\circ \\ &=\tan (180^\circ -30^\circ ) \\ &=-\tan 30^\circ \\ \tan \frac{5}{6}\pi &= -\frac{1}{3}\sqrt{3} \end{align}$
Cara 2.
$\begin{align}\tan \frac{5}{6}\pi &= \tan \frac{5}{6}\times 180^\circ \\ &=\tan 150^\circ \\ &=\tan (90^\circ +60{}^\circ ) \\ &=-\cot 60^\circ \\ \tan \frac{5}{6}\pi &= -\frac{1}{3}\sqrt{3} \end{align}$

Contoh 3.

Nilai dari $\sin 240^\circ $ = ...
Penyelesaian:
Cara 1.
$\begin{align}\sin 240^\circ &=\sin (180^\circ +60^\circ ) \\ &=-\sin 60^\circ \\ \sin 240^\circ &= -\frac{1}{2}\sqrt{3} \end{align}$
Cara 2.
$\begin{align}\sin 240^\circ &=\sin (270^\circ -30^\circ ) \\ &=-\cos 30^\circ \\ \sin 240^\circ &=-\frac{1}{2}\sqrt{3} \end{align}$

Contoh 4.

Tentukan nilai dari $\frac{\sin 150^\circ +\cos 300^\circ }{\tan 225^\circ -\sin 300^\circ }$ = ...
Penyelesaian:
$\frac{\sin 150^\circ +\cos 300^\circ }{\tan 225^\circ -\sin 300^\circ }$
= $\frac{\sin (180^\circ -30^\circ )+\cos (360^\circ -60^\circ )}{\tan (180^\circ +45^\circ )-\sin (360^\circ -60^\circ )}$
= $\frac{\sin 30^\circ +\cos 60^\circ }{\tan 45^\circ -(-\sin 60^\circ )}$
= $\frac{\frac{1}{2}+\frac{1}{2}}{1+\frac{1}{2}\sqrt{3}}$
= $\frac{2}{2+\sqrt{3}}$
= $\frac{2}{2+\sqrt{3}}\times \frac{2-\sqrt{3}}{2-\sqrt{3}}$
= $\frac{4-2\sqrt{3}}{4-3}$
= $4-2\sqrt{3}$

Contoh 5.

Jika $\tan 24^\circ =k$ maka $\cos 294{}^\circ $ = ...
(A) $\frac{k}{\sqrt{1-k^2}}$
(B) $\frac{k}{\sqrt{k^2+1}}$
(C) $\sqrt{1+k^2}$
(D) $\sqrt{1-k^2}$
(E) 1
Penyelesaian:
$\tan 24^\circ =\frac{k}{1}=\frac{de}{sa}$
$mi=\sqrt{de^2+sa^2}=\sqrt{k^2+1}$
$\begin{align}\cos 294^\circ &=\cos (270^\circ +24^\circ ) \\ &=\sin 24^\circ \\ &=\frac{de}{mi} \\ \cos 294^\circ &=\frac{k}{\sqrt{k^2+1}} \end{align}$
Jawaban: B

Contoh 6.

Nilai dari $\cos 1200{}^\circ $ = ....
Penyelesaian:
$\begin{align}\cos 1200^\circ &=\cos (3\times 360^\circ +120^\circ ) \\ &=\cos 120^\circ \\ &=\cos (180^\circ -60{}^\circ ) \\ &=-\cos 60^\circ \\ \cos 1200^\circ &=-\frac{1}{2} \end{align}$

G. Soal Latihan

1. Hitunglah nilai dari $\sin 330^\circ .\cos 60^\circ -\tan 135^\circ $.
2. Hitunglah nilai dari $\sin 765^\circ $.
3. Diketahui $\cos 36^\circ =0,8$. Dengan konsep sudut relasi, tentukan nilai dari $\cos 144^\circ $ dan $\sin 306^\circ $.
4. Diketahui $\tan \beta =\frac{4}{3}$, dengan $\beta $ sudut di kuadran I, tentukanlah nilai dari $\sin \left( \frac{\pi }{2}-\beta \right)$ dan $\tan \left( 2\pi -\beta \right)$.
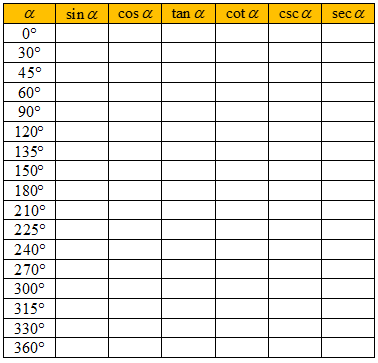
5. Dengan menggunakan konsep relasi sudut, lengkapilah tabel berikut ini!

by: Catatan Matematika

Semoga postingan: Perbandingan Trigonometri Sudut Berelasi ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.