Luas Segitiga dan Pembuktian Rumus

Rumus Luas Segitiga-Pembuktian Rumus-Contoh Soal-dan Latihan

A. Luas Segitiga dengan Alas dan Tinggi Diketahui

Perhatikan gambar berikut!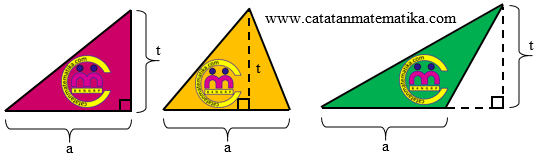
Rumus Luas Segitiga Alas x Tinggi per 2

Pada masing-masing segitiga diketahui a = alas segitiga dan t = tinggi segitiga. (Ingat: alas dan tinggi saling tegak lurus), maka luas segitiga adalah:
$L=\frac{1}{2}\times alas\times tinggi$ atau $L=\frac{1}{2}at$
Bukti:
Perhatikan gambar berikut!
Pembuktian Rumus Luas Segitiga

Konsep dasar luas bidang datar adalah panjang x lebar.
Luas persegi panjang ABCD adalah:
$L_{ABCD}=AB\times BC\Leftrightarrow L=a\times t$
Luas ABC = Luas ADC, sehingga:
$\begin{align}2\times L_{ABC} &=L_{ABCD} \\ L_{ABC} &=\frac{1}{2}.L_{ABCD} \\ L_{ABC} &=\frac{1}{2}at \end{align}$
(terbukti).

Contoh:
Diketahui segitiga ABC dengan panjang AC = BC = 6 cm, AB = $6\sqrt{3}$ cm. Luas segitiga ABC tersebut adalah ... $\text{cm}^2$.
Penyelesaian:
Perhatikan gambar berikut!
Contoh Soal Luas Segitiga

$DB=\frac{1}{2}.AB=\frac{1}{2}.6\sqrt{3}=3\sqrt{3}$
$\begin{align}CD &=\sqrt{BC^2-DB^2} \\ &=\sqrt{6^2-(3\sqrt{3})^2} \\ &=\sqrt{36-27} \\ CD &=3 \end{align}$
$\begin{align} L &=\frac{1}{2}.AB.CD \\ &=\frac{1}{2}.6\sqrt{3}.3 \\ L &=9\sqrt{3} \end{align}$
Jadi, luas segitiga ABC adalah $9\sqrt{3}$ $\text{cm}^2$.

B. Luas Segitiga dengan Besar Sudut dan Dua Sisi yang Mengapit Sudut itu Diketahui

Pada segitiga ABC, AB = c, BC = a dan AC = b.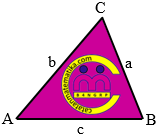
Rumus Luas Segitiga dengan Besar Sudut dan Dusa Sisi yang Mengapit Sudut itu Diketahui

Luas segitiga ABC adalah:
$L=\frac{1}{2}bc\sin A$
$L=\frac{1}{2}ac\sin B$
$L=\frac{1}{2}ab\sin C$
Bukti:
(1) Pembuktian: $L=\frac{1}{2}bc\sin A$
Perhatikan gambar berikut!
Pembuktian Rumus Luas Segitiga 1

Lihat segitiga ADC:
$\begin{align}\sin A &=\frac{CD}{AC} \\ CD &=AC.\sin A \\ CD &=b.\sin A \end{align}$
$\begin{align} L_{ABC} &=\frac{1}{2}\times alas\times tinggi \\ &=\frac{1}{2}.AB.CD \\ &=\frac{1}{2}.c.b\sin A \\ L_{ABC} &=\frac{1}{2}bc\sin A \end{align}$
(terbukti)

(2) Pembuktian: $L=\frac{1}{2}ac\sin B$
Perhatikan gambar berikut!
Pembuktian Rumus Luas Segitiga 2

Perhatikan segitiga BDC:
$\begin{align}\sin B &= \frac{DC}{BC} \\ CD &=BC.\sin B \\ CD &=a.\sin B \end{align}$
$\begin{align} L_{ABC} &=\frac{1}{2}.AB\times CD \\ &=\frac{1}{2}.c.a\sin B \\ L_{ABC}&=\frac{1}{2}ac\sin B \end{align}$
(terbukti)

(3) Pembuktian: $L=\frac{1}{2}ab\sin C$
Perhatikan gambar berikut!
Pembuktian Rumus Luas Segitiga 3

Perhatikan segitiga BEC:
$\begin{align}\sin C &=\frac{BE}{BC} \\ BE &=BC.\sin C \\ BE &=a.\sin C \end{align}$
$\begin{align}L_{ABC} &=\frac{1}{2}.AC\times BE \\ &=\frac{1}{2}.b.a\sin C \\ L_{ABC} &=\frac{1}{2}ab\sin C \end{align}$
(terbukti)

Contoh:
Diketahui segitiga PQR dengan panjang sisi PQ = 6, PR = 4 dan $\angle RPQ=45^\circ $, maka luas segitiga PQR adalah ... satuan luas.
Penyelesaian:
Perhatikan gambar berikut!
Contoh 2. Luas Segitiga

Luas segitiga PQR adalah:
$\begin{align}L &=\frac{1}{2}qr.\sin P \\ &=\frac{1}{2}.4.6.\sin 45^\circ \\ &=12.\frac{1}{2}\sqrt{2} \\ L &=6\sqrt{2} \end{align}$
Jadi, luas segitiga PQR adalah $6\sqrt{2}$ satuan luas.

C. Luas Segitiga dengan Besar Dua Sudut dan Satu Sisi yang Terletak di antara Kedua Sudut Diketahui

Pada segitiga ABC, AB = c, BC = a dan AC = b.
Luas Segitiga dengan Besar Dua Sudut dan Satu Sisi yang Terletak di antara Kedua Sudut Diketahui

Luas segitiga ABC adalah:
$L=\frac{a^2.\sin B\sin C}{2\sin A}$
$L=\frac{b^2.\sin A\sin C}{2\sin B}$
$L=\frac{c^2.\sin A\sin B}{2\sin C}$
Bukti:
(1) Pembuktian: $L=\frac{a^2.\sin B\sin C}{2\sin A}$
Ingat: Aturan Sinus
$\frac{b}{\sin B}=\frac{a}{\sin A}\Leftrightarrow b=\frac{a\sin B}{\sin A}$
$\begin{align}L &=\frac{1}{2}ab\sin C \\ &=\frac{1}{2}a.\frac{a\sin B}{\sin A}.\sin C \\ L &=\frac{a^2.\sin B\sin C}{2\sin A} \end{align}$
(terbukti)

(2) Pembuktian: $L=\frac{b^2.\sin A\sin C}{2\sin B}$
Ingat: Aturan Sinus
$\frac{c}{\sin C}=\frac{b}{\sin B}\Leftrightarrow c=\frac{b\sin C}{\sin B}$
$\begin{align}L &=\frac{1}{2}bc\operatorname{sinA} \\ &=\frac{1}{2}b.\frac{b\sin C}{\sin B}.\sin A \\ L &=\frac{b^2.\sin A\sin C}{2\sin B} \end{align}$
(terbukti)

(3) Pembuktian: $L=\frac{c^2.\sin A\sin B}{2\sin C}$
Ingat: Aturan Sinus
$\frac{a}{\sin A}=\frac{c}{\sin C}\Leftrightarrow a=\frac{c\sin A}{\sin C}$
$\begin{align}L &=\frac{1}{2}ac\sin B \\ &=\frac{1}{2}.\frac{c\sin A}{\sin C}.c.\sin B \\ L &=\frac{c^2.\sin A\sin B}{2\sin C} \end{align}$
(terbukti)

Contoh:
Diketahui segitiga ABC dengan panjang AB = 6 cm, besar $\angle A=30^\circ $ dan $\angle C=120^\circ $. Luas segitiga ABC adalah ... $\text{cm}^2$.
Penyelesaian:
Contoh 3. Soal Luas Segitiga

$\begin{align}\angle A+\angle B+\angle C &= 180^\circ \\ 30^\circ +\angle B+120^\circ &= 180^\circ \\ 150^\circ +\angle B &=180^\circ \\ \angle B &=180^\circ -150^\circ \\ \angle B &=30^\circ \end{align}$
Luas segitiga ABC adalah:
$\begin{align}L &=\frac{c^2.\sin A.\sin B}{2.\sin C} \\ &=\frac{6^2.\sin 30^\circ .\sin 30^\circ }{2.\sin 120^\circ } \\ &=\frac{36.\frac{1}{2}.\frac{1}{2}}{2.\frac{1}{2}\sqrt{3}} \\ &=\frac{9}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ L &=3\sqrt{3} \end{align}$
Jadi, luas segitiga ABC adalah $3\sqrt{3}$ $\text{cm}^2$.

D. Luas Segitiga dengan Ketiga Sisi Diketahui

Rumus Heron
Pada segitiga ABC, AB = c, BC = a dan AC = b.
Luas Segitiga Rumus Heron dan Pembuktian Rumus Heron

Luas segitiga ABC adalah:
$L=\sqrt{s(s-a)(s-b)(s-c)}$, dimana s adalah setengah keliling segitiga ABC, yaitu: $s=\frac{1}{2}(a+b+c)$.
Pembuktian Rumus Heron:
Dari aturan cosinus:
$\begin{align}a^2 &=b^2+c^2-2bc\cos A \\ 2bc\cos A &=b^2+c^2-a^2 \\ \cos A &=\frac{b^2+c^2-a^2}{2bc} \end{align}$
Identitas Trigonometri:
${{\sin }^{2}}A=1-{{\cos }^{2}}A$
$=(1-\cos A)(1+\cos A)$
$=\left( 1-\frac{b^2+c^2-a^2}{2bc} \right)\left( 1+\frac{b^2+c^2-a^2}{2bc} \right)$
$=\left( \frac{2bc}{2bc}-\frac{b^2+c^2-a^2}{2bc} \right)\left( \frac{2bc}{2bc}+\frac{b^2+c^2-a^2}{2bc} \right)$
$=\left( \frac{2bc-b^2-c^2+a^2}{2bc} \right)\left( \frac{2bc+b^2+c^2-a^2}{2bc} \right)$
$=\left( \frac{a^2-(b^2-2bc+c^2)}{2bc} \right)\left( \frac{b^2+2bc+c^2-a^2}{2bc} \right)$
$=\left( \frac{a^2-(b-c)^2}{2bc} \right)\left( \frac{(b+c)^2-a^2}{2bc} \right)$
$=\left( \frac{(a+b-c)(a-b+c)}{2bc} \right)\left( \frac{(b+c+a)(b+c-a)}{2bc} \right)$
$=\frac{(a+b-c)(a-b+c)(b+c+a)(b+c-a)}{(2bc)^2}$
$=\frac{(a+b+c-2c)(a+b+c-2b)(a+b+c)(a+b+c-2a)}{(2bc)^2}$
Misal: $a+b+c=2s$, maka:
$=\frac{(2s-2c)(2s-2b)(2s)(2s-2a)}{(2bc)^2}$
$=\frac{2(s-c)2(s-b)2(s)2(s-a)}{(2bc)^2}$
$=\frac{16s(s-a)(s-b)(s-c)}{4(bc)^2}$
${\sin }^{2}A=\frac{4s(s-a)(s-b)(s-c)}{(bc)^2}$
$\sin A=\sqrt{\frac{4s(s-a)(s-b)(s-c)}{(bc)^2}}$
$\sin A=\frac{2}{bc}\sqrt{s(s-a)(s-b)(s-c)}$
Luas segitiga adalah:
$\begin{align}L &=\frac{1}{2}.bc.\sin A \\ &=\frac{1}{2}bc.\frac{2}{bc}\sqrt{s(s-a)(s-b)(s-c)} \\ L &=\sqrt{s(s-a)(s-b)(s-c)} \end{align}$
(terbukti)

Contoh:
Segitiga XYZ mempunyai panjang masing-masing sisinya adalah XY = 4 cm, YZ = 5 cm, dan XZ = 7 cm. Tentukan luas segitiga XYZ.
Penyelesaian:
Contoh Soal Luas Segitiga Jika Diketahui Panjang Ketiga Sisinya

Contoh Soal Luas Segitiga Jika Diketahui Panjang Ketiga Sisinya

$\begin{align}s &=\frac{1}{2}(x+y+z) \\ &= \frac{1}{2}(5+7+4) \\ s &=8 \end{align}$
Luas segitiga XYZ adalah:
$\begin{align}L &=\sqrt{s(s-x)(s-y)(s-z)} \\ &=\sqrt{8(8-5)(8-7)(8-4)} \\ &=\sqrt{8.3.1.4} \\ &=\sqrt{96} \\ &=\sqrt{16\times 6} \\ L &=4\sqrt{6} \end{align}$
Jadi, luas segitiga XYZ adalah $4\sqrt{6}$ $\text{cm}^2$.

E. Soal Latihan Luas Segitiga

Diketahui $\Delta PQR$ siku-siku di Q, dengan PQ = 12 cm dan PR = 15 cm. Titik S terletak pada garis PR sehingga $QS\bot PR$. Tentukan luas $\Delta PQR$ dan panjang QS.
Diketahui $\Delta KLM$, dengan KL = 20 cm, KM = 12 cm, dan $\angle LKM=30^\circ $. Hitunglah luas $\Delta KLM$ tersebut.
Diketahui $\Delta ABC$ dengan $\angle A=35^\circ $, $\angle B = 78^\circ $ dan BC = 24 cm. Hitunglah luas segitiga ABC (gunakan kalkulator).
Diberikan segitiga ABC dengan AB = 41 cm, BC = 52 cm, dan AC = 15 cm. Hitunglah luas segitiga ABC.
Diketahui segiempat ABCD dengan AB // DC dan AD // BC. Jika AB = 18 cm, BC = 12 cm, dan $\angle ABC=150{}^\circ $, hitunglah luas ABCD.

by: Catatan Matematika

Semoga postingan: Luas Segitiga dan Pembuktian Rumus ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

CATATAN MATEMATIKA