Soal Jarak Titik ke Bidang pada Dimensi Tiga dan Pembahasan
Berikut ini adalah Kumpulan Soal Jarak Titik ke Bidang pada Dimensi Tiga dan Pembahasannya. Bagi adik-adik silahkan dipelajari dan jangan lupa share/bagikan ke media sosial kalian, agar manfaat postingan ini dapat dirasakan oleh siswa/i yang lain. Terima kasih.
(A) $\sqrt{3}$
(B) $2\sqrt{3}$
(C) $3\sqrt{3}$
(D) $4\sqrt{3}$
(E) $6\sqrt{3}$

Jarak titik E ke bidang BDG adalah:
= jarak titik E ke garis GK
= jarak titik E ke L
= EL
AC dan EG adalah diagonal sisi kubus maka:
$AC=s\sqrt{2}=6\sqrt{2}$
$EG=s\sqrt{2}=6\sqrt{2}$
$MG=\frac{1}{2}EG=3\sqrt{2}$
MK = CG = 6
Segitiga KMG siku-siku di titik M maka:
$\begin{align}GK &= \sqrt{MG^2+MK^2} \\ &= \sqrt{\left( 3\sqrt{2} \right)^2+6^2} \\ &= \sqrt{54} \\ GK &= 3\sqrt{6} \end{align}$
Perhatikan segitiga EKG:
Luas segitiga EKG adalah:
$\begin{align}\frac{1}{2}\times GK\times EL &= \frac{1}{2}\times EG\times MK \\ GK\times EL &= EG\times MK \\ 3\sqrt{6}\times EL &= 6\sqrt{2}\times 6 \\ EL &= \frac{36\sqrt{2}}{3\sqrt{6}} \\ &= \frac{12}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ EL &= 4\sqrt{3} \end{align}$
Jadi, jarak titik E ke bidang BDG adalah $4\sqrt{3}$ cm.
Cara alternatif:
Jarak titik E ke BDG pada kubus ABCD.EFGH adalah $\frac{2}{3}s\sqrt{3}=\frac{2}{3}.6\sqrt{3}=4\sqrt{3}$.
Jawaban: D
(A) $4\sqrt{5}$
(B) $4\sqrt{6}$
(C) $6\sqrt{5}$
(D) $6\sqrt{6}$
(E) $8\sqrt{5}$

Jarak titik H ke bidang ACQ = Jarak titik H ke garis PQ.
Titik Q adalah titik tengah BF maka:
$BQ=FQ=\frac{1}{2}BF=6$
Titik P adalah titik tengah BD maka:
$BP=DP=\frac{1}{2}.BD=6\sqrt{2}$
Segitiga PBQ siku-siku di titik B maka:
$\begin{align}PQ &= \sqrt{BP^2+BQ^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+6^2} \\ PQ &= \sqrt{108} \end{align}$
Segitiga PDH siku-siku di titik D maka:
$\begin{align}PH &= \sqrt{DP^2+DH^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+12^2} \\ PH &= \sqrt{216} \end{align}$
Segitiga HFQ siku-siku di titik F maka:
$\begin{align}HQ &= \sqrt{FQ^2+FH^2} \\ &= \sqrt{6^2+\left( 12\sqrt{2} \right)^2} \\ HQ &= \sqrt{324} \end{align}$
Jika diperhatikan ukuran sisi-sisi segitiga HPQ yaitu: $HQ=\sqrt{324}$, $PH=\sqrt{216}$ dan $PQ=\sqrt{108}$ memenuhi teorema pythagoras:
$\begin{align}HQ^2 &= PH^2+PQ^2 \\ 324 &= 216+108 \\ 324 &= 324 \end{align}$
Karena sisi terpanjang adalah HQ, maka dapat disimpulkan bahwa sudut siku-siku terletak pada titik P dan $PH\bot PQ$.
Jadi, jarak titik H ke garis PQ adalah panjang ruas garis PH yaitu $\sqrt{216}=6\sqrt{6}$ cm.
Jawaban: D
(A) $\frac{10}{3}\sqrt{2}$
(B) $\frac{10}{3}\sqrt{3}$
(C) $\frac{20}{3}\sqrt{2}$
(D) $\frac{20}{3}\sqrt{3}$
(E) $10\sqrt{2}$

Jarak titik A ke bidang CFH adalah:
= Jarak titik A ke garis PC
= Jarak titik A ke titik R
= AR
CA dan GE adalah diagonal kubus maka:
$CA=s\sqrt{2}=10\sqrt{2}$
$GE=s\sqrt{2}=10\sqrt{2}$
$GP=\frac{1}{2}GE=5\sqrt{2}$
Segitiga CGP siku-siku di titik G maka:
$\begin{align}PC &= \sqrt{CG^2+GP^2} \\ &= \sqrt{10^2+\left( 5\sqrt{2} \right)^2} \\ &= \sqrt{150} \\ PC &= 5\sqrt{6} \end{align}$
Perhatikan segitiga CPA:
Luas segitiga CPA:
$\begin{align}\frac{1}{2}\times PC\times AR &= \frac{1}{2}\times CA\times PQ \\ PC\times AR &= CA\times PQ \\ 5\sqrt{6}\times AR &= 10\sqrt{2}\times 10 \\ AR &= \frac{100\sqrt{2}}{5\sqrt{6}} \\ &= \frac{20}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ AR &= \frac{20}{3}\sqrt{3} \end{align}$
Jadi, jarak titik A ke bidang CFH adalah $\frac{20}{3}\sqrt{3}$ cm.
Cara alternatif:
Jarak titik A ke bidang CFH pada kubus ABCD.EFGH adalah $\frac{2}{3}s\sqrt{3}=\frac{2}{3}.10\sqrt{3}=\frac{20}{3}\sqrt{3}$.
Jawaban: D
(A) $\frac{5}{4}\sqrt{6}$
(B) $\frac{5}{3}\sqrt{3}$
(C) $\frac{5}{2}\sqrt{2}$
(D) $\frac{5}{3}\sqrt{6}$
(E) $5\sqrt{2}$

Jarak titik A ke bidang TBC adalah:
= jarak titik A ke garis TD
= jarak titik A ke titik E
= panjang ruas garis AE
Perhatikan segitiga BAC siku-siku di A maka $AD=\frac{5}{2}\sqrt{2}$.
Perhatikan segitiga TAD, siku-siku di A maka:
$\begin{align}TD &= \sqrt{AT^2+AD^2} \\ &= \sqrt{5^2+\left( \frac{5}{2}\sqrt{2} \right)^2} \\ &= \sqrt{25+\frac{25}{2}} \\ &= \sqrt{\frac{75}{2}} \\ &= \frac{5\sqrt{3}}{\sqrt{2}} \\ TD &= \frac{5}{2}\sqrt{6} \end{align}$
$\begin{align}AE &= \frac{AT\times AD}{TD} \\ &= \frac{5\times \frac{5}{2}\sqrt{2}}{\frac{5}{2}\sqrt{6}} \\ &= \frac{5}{\sqrt{3}} \\ AE &= \frac{5}{3}\sqrt{3} \end{align}$
Jadi, jarak titik A ke bidang TBC adalah $\frac{5}{3}\sqrt{3}$ cm.
Cara alternatif:
Perhatikan $AT\bot AB\bot AC$ maka jarak titik A ke bidang TBC adalah:
= $\frac{1}{\sqrt{\frac{1}{AT^2}+\frac{1}{AB^2}+\frac{1}{AC^2}}}$
= $\frac{1}{\sqrt{\frac{1}{5^2}+\frac{1}{5^2}+\frac{1}{5^2}}}$
= $\frac{1}{\frac{\sqrt{3}}{5}}$
= $\frac{5}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
= $\frac{5}{3}\sqrt{3}$
Jawaban: B
(A) $\frac{9}{2}\sqrt{6}$
(B) $\frac{9}{2}\sqrt{2}$
(C) $2\sqrt{3}$
(D) $\sqrt{6}$
(E) $4\sqrt{3}$

Jarak titik G ke bidang PQR adalah:
= Jarak titik G ke garis QS
= Jarak titik G ke titik T
= GT
GE adalah diagonal sisi kubus maka:
$GE=s\sqrt{2}=12\sqrt{2}$
Perhatikan segitiga RGP, luasnya adalah:
$\begin{align}\frac{1}{2}\times PR\times GS &= \frac{1}{2}\times GP\times GR \\ GS &= \frac{GP\times GR}{PR} \\ &= \frac{6\times 6}{6\sqrt{2}} \\ GS &= 3\sqrt{2} \end{align}$
Segitiga QGS siku-siku di titik G maka:
$\begin{align}QS &= \sqrt{GQ^2+GS^2} \\ &= \sqrt{6^2+\left( 3\sqrt{2} \right)^2} \\ &= \sqrt{54} \\ QS &= 3\sqrt{6} \end{align}$
Luas segitiga QGS adalah:
$\begin{align}\frac{1}{2}\times QS\times GT &= \frac{1}{2}\times GQ\times GS \\ QS\times GT &= GQ\times GS \\ 3\sqrt{6}\times GT &= 6\times 3\sqrt{2} \\ GT &= \frac{18\sqrt{2}}{3\sqrt{6}} \\ &= \frac{6}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ GT &= 2\sqrt{3} \end{align}$
Jadi, jarak titik G ke bidang PQR adalah $2\sqrt{3}$ cm.
Cara alternatif:
Perhatikan bahwa $GP\bot GQ\bot GR$ maka jarak titik G ke bidang PQR adalah:
= $\frac{1}{\sqrt{\frac{1}{GP^2}+\frac{1}{GR^2}+\frac{1}{GQ^2}}}$
= $\frac{1}{\sqrt{\frac{1}{6^2}+\frac{1}{6^2}+\frac{1}{6^2}}}$
= $\frac{1}{\sqrt{\frac{3}{36}}}$
= $\frac{1}{\frac{\sqrt{3}}{6}}$
= $\frac{6}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
= $2\sqrt{3}$
Jawaban: C
(A) 5 cm
(B) 5,5 cm
(C) 7,5 cm
(D) $5\sqrt{3}$ cm
(E) $10\sqrt{3}$ cm

Jarak titik A ke bidang TBC adalah:
= jarak titik A ke garis TD
= jarak titik A ke titik E
= panjang ruas garis AE
ABC segitiga sama sisi maka:
AD garis tinggi membagi dua sisi BC.
$\begin{align}AD &= \sqrt{AB^2-BD^2} \\ &= \sqrt{10^2-5^2} \\ &= \sqrt{75} \\ AD &= 5\sqrt{3} \end{align}$
Perhatikan segitiga TAD, siku-siku di A maka:
$\begin{align}TD &= \sqrt{AT^2+AD^2} \\ &= \sqrt{15^2+\left( 5\sqrt{3} \right)^2} \\ &= \sqrt{300} \\ TD &= 10\sqrt{3} \end{align}$
Luas segitiga TAD:
$\begin{align}\frac{1}{2}\times TD\times AE &= \frac{1}{2}\times AD\times AT \\ TD\times AE &= AD\times AT \\ 10\sqrt{3}\times AE &= 5\sqrt{3}\times 15 \\ AE &= 7,5 \end{align}$
Jadi, jarak titik A ke bidang TBC adalah 7,5 cm.
Jawaban: C
(A) 1
(B) 2
(C) $\sqrt{2}$
(D) $\sqrt{3}$
(E) $2\sqrt{2}$
$\begin{align}TP+PC &= TC \\ 2a+a &= 6 \\ 3a &= 6 \\ a &= 2 \end{align}$
Maka TP = 4 cm dan PC = 2 cm.
Perhatikan gambar berikut!

Jarak titik P ke bidang BDT
= jarak titik P ke garis TO
= jarak titik P ke titik Q
= PQ
Segitiga ABC siku-siku di titik B maka:
$\begin{align}AC &= \sqrt{AB^2+BC^2} \\ &= \sqrt{6^2+6^2} \\ AC &= 6\sqrt{2} \end{align}$
$OC=\frac{1}{2}AC=3\sqrt{2}$
Segitiga TOC sebangun dengan segitiga TQP maka perbandingan sisinya adalah:
$\begin{align}\frac{PQ}{CO} &= \frac{TP}{TC} \\ \frac{PQ}{3\sqrt{2}} &= \frac{4}{6} \\ PQ &= 2\sqrt{2} \end{align}$
Jadi, jarak titik P ke bidang BDT adalah $2\sqrt{2}$ cm.
Jawaban: E
(A) 1
(B) 2/3
(C) 1/2
(D) 3/4
(E) 1/4

Jarak titik E ke bidang MNA adalah:
= Jarak titik E ke garis AP
= Jarak titik E ke titik Q
= EQ
Perhatikan segitiga MEN;
$\begin{align}EP &= \frac{EM\times EN}{MN} \\ &= \frac{1\times 1}{\sqrt{2}} \\ EP &= \frac{1}{2}\sqrt{2} \end{align}$
Segitiga AEP siku-siku di titik E maka:
$\begin{align}AP &= \sqrt{AE^2+EP^2} \\ &= \sqrt{2^2+\left( \frac{1}{2}\sqrt{2} \right)^2} \\ &= \sqrt{\frac{9}{2}} \\ &= \frac{3}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ AP &= \frac{3}{2}\sqrt{2} \end{align}$
Luas segitiga AEP adalah:
$\begin{align}\frac{1}{2}\times AP\times EQ &= \frac{1}{2}\times EP\times AE \\ EQ &= \frac{EP\times AE}{AP} \\ &= \frac{\frac{1}{2}\sqrt{2}\times 2}{\frac{3}{2}\sqrt{2}} \\ EQ &= \frac{2}{3} \end{align}$
Jadi, jarak titik E ke bidang MNA adalah 2/3 cm.
Cara alternatif:
$EA\bot EM\bot EN$ maka jarak titik E ke bidang MNA adalah:
= $\frac{1}{\sqrt{\frac{1}{EA^2}+\frac{1}{EM^2}+\frac{1}{EN^2}}}$
= $\frac{1}{\sqrt{\frac{1}{2^2}+\frac{1}{1^2}+\frac{1}{1^2}}}$
= $\frac{1}{\sqrt{\frac{9}{4}}}$
= $\frac{2}{3}$
Jawaban: B
(A) $\sqrt{3}$
(B) 3
(C) 4
(D) $2\sqrt{5}$
(E) $2\sqrt{7}$

Jarak titik H ke bidang APQE adalah:
= Jarak titik H ke garis EQ
= Jarak titik H ke titik R
= HR
Luas EHQ = $\frac{1}{2}\times 2\sqrt{3}\times 2\sqrt{3}$ = 6
Segitiga EFQ siku-siku di titik F maka:
$\begin{align}EQ &= \sqrt{EF^2+FQ^2} \\ &= \sqrt{\left( 2\sqrt{3} \right)^2+2^2} \\ EQ &= 4 \end{align}$
Perhatikan segitiga EHQ
$\begin{align}\text{Luas}\,\text{EHQ} &= \frac{1}{2}\times EQ\times HR \\ 6 &= \frac{1}{2}\times 4\times HR \\ 3 &= HR \end{align}$
Jadi, jarak titik H ke bidang APQE adalah 3 cm.
Jawaban: B
(A) $2s\sqrt{3}$
(B) $3s\sqrt{3}$
(C) $3\sqrt{s}$
(D) $\frac{1}{2}s\sqrt{3}$
(E) $\frac{1}{3}s\sqrt{3}$

Jarak titik A ke bidang BED adalah:
= Jarak titik A ke garis PE
= Jarak titik A ke titik Q
= AQ
AC adalah diagonal kubus maka:
$AC=s\sqrt{2}$
$AP=\frac{1}{2}AC=\frac{1}{2}s\sqrt{2}$
Segitiga EAP siku-siku di titik E maka:
$\begin{align}PE &= \sqrt{AP^2+AE^2} \\ &= \sqrt{\left( \frac{1}{2}s\sqrt{2} \right)^2+s^2} \\ &= \sqrt{\frac{6s^2}{4}} \\ PE &= \frac{1}{2}s\sqrt{6} \end{align}$
Luas segitiga EAP:
$\begin{align}\frac{1}{2}\times PE\times AQ &= \frac{1}{2}\times AP\times AE \\ AQ &= \frac{AP\times AE}{PE} \\ &= \frac{\frac{1}{2}s\sqrt{2}\times s}{\frac{1}{2}s\sqrt{6}} \\ &= \frac{s}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ AQ &= \frac{1}{3}s\sqrt{3} \end{align}$
Jadi, jarak titik A ke bidang BED adalah $\frac{1}{3}s\sqrt{3}$ cm.
Cara alternatif:
$AB\bot AE\bot AD$ maka jarak titik A ke BED adalah:
= $\frac{1}{\sqrt{\frac{1}{AB^2}+\frac{1}{AE^2}+\frac{1}{AD^2}}}$
= $\frac{1}{\sqrt{\frac{1}{s^2}+\frac{1}{s^2}+\frac{1}{s^2}}}$
= $\frac{1}{\sqrt{\frac{3}{{{s}^{2}}}}}$
= $\frac{s}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
= $\frac{1}{3}s\sqrt{3}$
Jawaban: E
(A) $\frac{4}{3}\sqrt{3}$
(B) $\frac{3}{4}\sqrt{3}$
(C) $\frac{4}{3}\sqrt{2}$
(D) $\frac{3}{4}\sqrt{2}$
(E) $\frac{8}{3}$

Jarak titik C ke bidang BDG adalah:
= Jarak titik C ke garis PC
= Jarak titik C ke titik Q
= CQ
AC adalah diagonal sisi kubus maka:
$AC=s\sqrt{2}=4\sqrt{2}$
$PC=\frac{1}{2}AC=2\sqrt{2}$
Segitiga PCG siku-siku di titik C maka:
$\begin{align}PG &= \sqrt{PC^2+CG^2} \\ &= \sqrt{\left( 2\sqrt{2} \right)^2+4^2} \\ &= \sqrt{24} \\ PG &= 2\sqrt{6} \end{align}$
Luas segitiga PCG adalah:
$\begin{align}\frac{1}{2}\times PG\times CQ &= \frac{1}{2}\times PC\times CG \\ CQ &= \frac{PC\times CG}{PG} \\ &= \frac{2\sqrt{2}\times 4}{2\sqrt{6}} \\ &= \frac{4}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ CQ &= \frac{4}{3}\sqrt{3} \end{align}$
Jadi, jarak titik C ke bidang BDG adalah $\frac{4}{3}\sqrt{3}$ cm.
Cara alternatif:
$CB\bot CD\bot CG$ maka jarak titik C ke bidang BDG adalah:
= $\frac{1}{\sqrt{\frac{1}{CB^2}+\frac{1}{CD^2}+\frac{1}{CG^2}}}$
= $\frac{1}{\sqrt{\frac{1}{4^2}+\frac{1}{4^2}+\frac{1}{4^2}}}$
= $\frac{1}{\sqrt{\frac{3}{16}}}$
= $\frac{4}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
= $\frac{4}{3}\sqrt{3}$
Jawaban: A
(A) $\frac{1}{2}\sqrt{2}$
(B) $\frac{1}{2}\sqrt{3}$
(C) 1
(D) $\sqrt{2}$
(E) $\sqrt{3}$

Jarak titik A ke bidang PQRS adalah:
= Jarak titik A ke garis PS
= Jarak titik A ke titik T
= AT
Segitiga PAS siku-siku di titik A maka:
$\begin{align}PS &= \sqrt{AS^2+AP^2} \\ &= \sqrt{\left( \sqrt{3} \right)^2+1^2} \\ PS &= 2 \end{align}$
Luas segitiga PAS adalah:
$\begin{align}\frac{1}{2}\times PS\times AT &= \frac{1}{2}\times AS\times AP \\ AT &= \frac{AS\times AP}{PS} \\ &= \frac{\sqrt{3}\times 1}{2} \\ AT &= \frac{1}{2}\sqrt{3} \end{align}$
Jawaban: B
(A) $8\sqrt{3}$
(B) $\frac{16}{3}\sqrt{3}$
(C) $8\sqrt{2}$
(D) $\frac{16}{3}\sqrt{2}$
(E) $8\sqrt{3}$

Jarak titik F ke bidang ACH adalah:
= Jarak titik F ke garis PH
= Jarak titik F ke titik R
= FR
HF adalah diagonal sisi kubus, maka:
$HF=s\sqrt{2}=8\sqrt{2}$
Luas segitiga HPF = $\frac{1}{2}\times 8\sqrt{2}\times 8$ = $32\sqrt{2}$.
BD adalah diagonal sisi kubus maka:
$BD=s\sqrt{2}=8\sqrt{2}$
$DP=\frac{1}{2}BD=4\sqrt{2}$
Segitiga HDP siku-siku di titik D maka:
= $\begin{align}PH &= \sqrt{DP^2+DH^2} \\ &= \sqrt{\left( 4\sqrt{2} \right)^2+8^2} \\ &= \sqrt{96} \\ PH &= 4\sqrt{6} \end{align}$
$\begin{align}Luas\,HPE &= \frac{1}{2}\times PH\times FR \\ 32\sqrt{2} &= \frac{1}{2}\times 4\sqrt{6}\times FR \\ FR &= \frac{16}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ FR &= \frac{16}{3}\sqrt{3} \end{align}$
Jadi, jarak titik F ke bidang ACH adalah $\frac{16}{3}\sqrt{3}$ cm.
Jawaban: B
(A) $2\sqrt{6}$
(B) $2\sqrt{3}$
(C) $3\sqrt{2}$
(D) $3\sqrt{6}$
(E) $3\sqrt{3}$

Jarak titik P ke bidang TAB adalah:
= Jarak titik P ke garis TQ
= Jarak titik P ke titik R
= PR
segitiga AQT siku-siku di titik Q maka:
$\begin{align}TQ &= \sqrt{AT^2-AQ^2} \\ &= \sqrt{6^2-3^2} \\ &= \sqrt{27} \\ TQ &= 3\sqrt{3} \end{align}$
Segitiga TOQ siku-siku di titik O maka:
$\begin{align}TO &= \sqrt{TQ^2-OQ^2} \\ &= \sqrt{\left( 3\sqrt{3} \right)^2-3^2} \\ &= \sqrt{18} \\ TO &= 3\sqrt{2} \end{align}$
Luas segitiga TPQ adalah:
$\begin{align}\frac{1}{2}\times TQ\times PR &= \frac{1}{2}\times PQ\times TO \\ PR &= \frac{PQ\times TO}{TQ} \\ &= \frac{6\times 3\sqrt{2}}{3\sqrt{3}} \\ &= \frac{6\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ PR &= 2\sqrt{6} \end{align}$
Jadi, jarak titik P ke bidang TAB adalah $2\sqrt{6}$ cm.
Jawaban: A
(A) $\frac{4}{5}\sqrt{5}$
(B) $\frac{8}{5}\sqrt{5}$
(C) $\frac{4}{3}\sqrt{3}$
(D) $\frac{8}{3}\sqrt{3}$
(E) $\frac{4}{3}\sqrt{2}$

Jarak titik Q ke bidang BCP adalah:
= Jarak titik Q ke garis PR
= Jarak titik Q ke titik S
= QS
Segitiga PQR siku-siku di titik Q maka:
$\begin{align}PR &= \sqrt{PQ^2+QR^2} \\ &= \sqrt{8^2+4^2} \\ &= \sqrt{80} \\ PR &= 4\sqrt{5} \end{align}$
Luas segitiga PQR adalah:
$\begin{align}\frac{1}{2}\times PR\times QS &= \frac{1}{2}\times QR\times PQ \\ QS &= \frac{QR\times PQ}{PR} \\ &= \frac{4\times 8}{4\sqrt{5}} \\ &= \frac{8}{\sqrt{5}}\times \frac{\sqrt{5}}{\sqrt{5}} \\ QS &= \frac{8}{5}\sqrt{5} \end{align}$
Jadi, jarak titik Q ke bidang BCP adalah $\frac{8}{5}\sqrt{5}$ cm.
Jawaban: B
(A) $6\sqrt{2}$
(B) $9\sqrt{2}$
(C) $12\sqrt{2}$
(D) $16\sqrt{2}$
(E) $18\sqrt{2}$
Misal: CP = x maka DP = 3x
$\begin{align}DC &= DP-CP \\ 12 &= 3x-x \\ 12 &= 2x \\ 6 &= x \end{align}$
Jadi, panjang CP = x = 6 cm.
Perhatikan gambar berikut!

Jarak titik P ke bidang BDHF adalah:
= Jarak titik P ke garis BD
= Jarak titik P ke titik Q
= PQ
AC adalah diagonal sisi kubus maka:
$AC=s\sqrt{2}=12\sqrt{2}$
$CR=\frac{1}{2}AC=6\sqrt{2}$
Perhatikan:
Segitiga DQP sebangun dengan segitiga DRC maka perbandingan sisi-sisi yang bersesuaian adalah:
$\begin{align}\frac{PQ}{CR} &= \frac{DP}{DC} \\ PQ &= \frac{DP\times CR}{DC} \\ &= \frac{18\times 6\sqrt{2}}{12} \\ PQ &= 9\sqrt{2} \end{align}$
Jadi, jarak titik P ke bidang BDHF adalah $9\sqrt{2}$ cm.
Jawaban: B
(A) $\frac{3}{4}\sqrt{6}$
(B) $\sqrt{6}$
(C) $\frac{3}{2}\sqrt{2}$
(D) $3\sqrt{6}$
(E) $9\sqrt{2}$

Jarak titik A ke bidang TBC adalah:
= jarak titik A ke garis TD
= jarak titik A ke titik E
= panjang ruas garis AE
AD = 3 cm
Perhatikan segitiga TAD, siku-siku di A maka:
$\begin{align}TD &= \sqrt{AT^2+AD^2} \\ &= \sqrt{\left( 3\sqrt{2} \right)^2+3^2} \\ &= \sqrt{27} \\ TD &= 3\sqrt{3} \end{align}$
$\begin{align}AE &= \frac{AT\times AD}{TD} \\ &= \frac{3\sqrt{2}\times 3}{3\sqrt{3}} \\ &= \frac{3\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ AE &= \sqrt{6} \end{align}$
Jadi, jarak titik A ke bidang TBC adalah $\sqrt{6}$ cm.
Cara alternatif:
Perhatikan $AT\bot AB\bot AC$ maka jarak titik A ke bidang TBC adalah:
= $\frac{1}{\sqrt{\frac{1}{AT^2}+\frac{1}{AB^2}+\frac{1}{AC^2}}}$
= $\frac{1}{\sqrt{\frac{1}{\left( 3\sqrt{2} \right)^2}+\frac{1}{\left( 3\sqrt{2} \right)^2}+\frac{1}{\left( 3\sqrt{2} \right)^2}}}$
= $\sqrt{6}$
Jadi, jarak titik A ke bidang TBC adalah $\sqrt{6}$ cm.
Jawaban: B
(A) $6\sqrt{2}$
(B) $9\sqrt{2}$
(C) $3\sqrt{2}$
(D) $\frac{9}{2}\sqrt{2}$
(E) $12\sqrt{2}$
Misal: CP = x maka DP = 3x
$\begin{align}DC &= DP-CP \\ 6 &= 3x-x \\ 6 &= 2x \\ 3 &= x \end{align}$
Jadi, panjang CP = x = 3 cm.
Perhatikan gambar berikut!
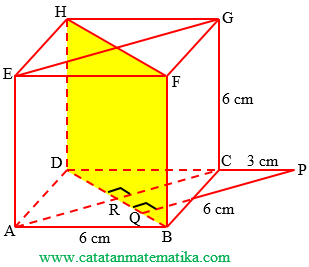
Jarak titik P ke bidang BDHF adalah:
= Jarak titik P ke garis BD
= Jarak titik P ke titik Q
= PQ
AC adalah diagonal sisi kubus maka:
$AC=s\sqrt{2}=6\sqrt{2}$
$CR=\frac{1}{2}AC=3\sqrt{2}$
Perhatikan:
Segitiga DQP sebangun dengan segitiga DRC maka perbandingan sisi-sisi yang bersesuaian adalah:
$\begin{align}\frac{PQ}{CR} &= \frac{DP}{DC} \\ PQ &= \frac{DP\times CR}{DC} \\ &= \frac{9\times 3\sqrt{2}}{6} \\ PQ &= \frac{9}{2}\sqrt{2} \end{align}$
Jadi, jarak titik P ke bidang BDHF adalah $\frac{9}{2}\sqrt{2}$ cm.
Jawaban: D
(A) a
(B) 2a
(C) 3a
(D) 4a
(E) 5a
$\begin{align}6s^2 &= 18a^2 \\ s^2 &= 3a^2 \\ s &= a\sqrt{3} \end{align}$
Jadi, rusuk kubus ABCD.EFGH adalah $a\sqrt{3}$ cm.
Perhatikan gambar berikut!

Jarak titik A ke bidang CFH adalah:
= Jarak titik A ke garis PC
= Jarak titik A ke titik R
= AR
CA dan GE adalah diagonal kubus maka:
$CA=s\sqrt{2}=a\sqrt{3}.\sqrt{2}=a\sqrt{6}$
$GE=s\sqrt{2}=a\sqrt{3}.\sqrt{2}=a\sqrt{6}$
$GP=\frac{1}{2}GE=\frac{1}{2}a\sqrt{6}$
Segitiga CGP siku-siku di titik G maka:
$\begin{align}PC &= \sqrt{CG^2+GP^2} \\ &= \sqrt{\left( a\sqrt{3} \right)^2+\left( \frac{1}{2}a\sqrt{6} \right)^2} \\ &= \sqrt{\frac{9a^2}{2}} \\ PC &= \frac{3a}{2}\sqrt{2} \end{align}$
Perhatikan segitiga CPA:
Luas segitiga CPA:
$\begin{align}\frac{1}{2}\times PC\times AR &= \frac{1}{2}\times CA\times PQ \\ AR &= \frac{CA\times PQ}{PC} \\ &= \frac{a\sqrt{6}\times a\sqrt{3}}{\frac{3a}{2}\sqrt{2}} \\ AR &= 2a \end{align}$
Jadi, jarak titik A ke bidang CFH adalah $2a$ cm.
Cara alternatif:
Jarak titik A ke bidang CFH pada kubus ABCD.EFGH adalah $\frac{2}{3}s\sqrt{3}=\frac{2}{3}.a\sqrt{3.}\sqrt{3}=2a$.
Jawaban: B
(A) $18\sqrt{2}$
(B) $12\sqrt{2}$
(C) 16
(D) 12
(E) $6\sqrt{2}$

Jarak titik G ke bidang BDE adalah:
= Jarak titik G ke garis PE
= Jarak titik G ke titik Q
= GQ
Perhatikan segitiga ABC:
$\begin{align}AC &= \sqrt{AB^2+BC^2} \\ &= \sqrt{12^2+12^2} \\ AC &= 12\sqrt{2} \end{align}$
$AP=\frac{1}{2}AC=6\sqrt{2}$
Perhatikan segitiga EAP:
$\begin{align}PE &= \sqrt{AE^2+AP^2} \\ &= \sqrt{24^2+\left( 6\sqrt{2} \right)^2} \\ &= \sqrt{576+72} \\ &= \sqrt{648} \\ PE &= 18\sqrt{2} \end{align}$
Luas segitiga PEG adalah:
$\begin{align}\frac{1}{2}\times PE\times GQ &= \frac{1}{2}\times EG\times PR \\ GQ &= \frac{EG\times PR}{PE} \\ &= \frac{12\sqrt{2}\times 24}{18\sqrt{2}} \\ GQ &= 16 \end{align}$
Jadi, jarak titik G ke bidang BDE adalah 16 cm.
Jawaban: C
Tata Cara Belajar:
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cocokkanlah jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
SELAMAT BELAJAR
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cocokkanlah jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
SELAMAT BELAJAR
Soal No. 1
Panjang rusuk kubus ABCD.EFGH adalah 6 cm. Jarak titik E ke bidang BDG adalah … cm.(A) $\sqrt{3}$
(B) $2\sqrt{3}$
(C) $3\sqrt{3}$
(D) $4\sqrt{3}$
(E) $6\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik E ke bidang BDG adalah:
= jarak titik E ke garis GK
= jarak titik E ke L
= EL
AC dan EG adalah diagonal sisi kubus maka:
$AC=s\sqrt{2}=6\sqrt{2}$
$EG=s\sqrt{2}=6\sqrt{2}$
$MG=\frac{1}{2}EG=3\sqrt{2}$
MK = CG = 6
Segitiga KMG siku-siku di titik M maka:
$\begin{align}GK &= \sqrt{MG^2+MK^2} \\ &= \sqrt{\left( 3\sqrt{2} \right)^2+6^2} \\ &= \sqrt{54} \\ GK &= 3\sqrt{6} \end{align}$
Perhatikan segitiga EKG:
Luas segitiga EKG adalah:
$\begin{align}\frac{1}{2}\times GK\times EL &= \frac{1}{2}\times EG\times MK \\ GK\times EL &= EG\times MK \\ 3\sqrt{6}\times EL &= 6\sqrt{2}\times 6 \\ EL &= \frac{36\sqrt{2}}{3\sqrt{6}} \\ &= \frac{12}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ EL &= 4\sqrt{3} \end{align}$
Jadi, jarak titik E ke bidang BDG adalah $4\sqrt{3}$ cm.
Cara alternatif:
Jarak titik E ke BDG pada kubus ABCD.EFGH adalah $\frac{2}{3}s\sqrt{3}=\frac{2}{3}.6\sqrt{3}=4\sqrt{3}$.
Jawaban: D
Soal No. 2
Pada kubus ABCD.EFGH panjang rusuknya 12 cm. Titik Q adalah titik tengah rusuk BF. Jarak titik H ke bidang ACQ sama dengan … cm.(A) $4\sqrt{5}$
(B) $4\sqrt{6}$
(C) $6\sqrt{5}$
(D) $6\sqrt{6}$
(E) $8\sqrt{5}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik H ke bidang ACQ = Jarak titik H ke garis PQ.
Titik Q adalah titik tengah BF maka:
$BQ=FQ=\frac{1}{2}BF=6$
Titik P adalah titik tengah BD maka:
$BP=DP=\frac{1}{2}.BD=6\sqrt{2}$
Segitiga PBQ siku-siku di titik B maka:
$\begin{align}PQ &= \sqrt{BP^2+BQ^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+6^2} \\ PQ &= \sqrt{108} \end{align}$
Segitiga PDH siku-siku di titik D maka:
$\begin{align}PH &= \sqrt{DP^2+DH^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+12^2} \\ PH &= \sqrt{216} \end{align}$
Segitiga HFQ siku-siku di titik F maka:
$\begin{align}HQ &= \sqrt{FQ^2+FH^2} \\ &= \sqrt{6^2+\left( 12\sqrt{2} \right)^2} \\ HQ &= \sqrt{324} \end{align}$
Jika diperhatikan ukuran sisi-sisi segitiga HPQ yaitu: $HQ=\sqrt{324}$, $PH=\sqrt{216}$ dan $PQ=\sqrt{108}$ memenuhi teorema pythagoras:
$\begin{align}HQ^2 &= PH^2+PQ^2 \\ 324 &= 216+108 \\ 324 &= 324 \end{align}$
Karena sisi terpanjang adalah HQ, maka dapat disimpulkan bahwa sudut siku-siku terletak pada titik P dan $PH\bot PQ$.
Jadi, jarak titik H ke garis PQ adalah panjang ruas garis PH yaitu $\sqrt{216}=6\sqrt{6}$ cm.
Jawaban: D
Soal No. 3
Diketahui kubus ABCD.EFGH dengan rusuk 10 cm. Jarak titik A ke bidang CFH adalah … cm.(A) $\frac{10}{3}\sqrt{2}$
(B) $\frac{10}{3}\sqrt{3}$
(C) $\frac{20}{3}\sqrt{2}$
(D) $\frac{20}{3}\sqrt{3}$
(E) $10\sqrt{2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik A ke bidang CFH adalah:
= Jarak titik A ke garis PC
= Jarak titik A ke titik R
= AR
CA dan GE adalah diagonal kubus maka:
$CA=s\sqrt{2}=10\sqrt{2}$
$GE=s\sqrt{2}=10\sqrt{2}$
$GP=\frac{1}{2}GE=5\sqrt{2}$
Segitiga CGP siku-siku di titik G maka:
$\begin{align}PC &= \sqrt{CG^2+GP^2} \\ &= \sqrt{10^2+\left( 5\sqrt{2} \right)^2} \\ &= \sqrt{150} \\ PC &= 5\sqrt{6} \end{align}$
Perhatikan segitiga CPA:
Luas segitiga CPA:
$\begin{align}\frac{1}{2}\times PC\times AR &= \frac{1}{2}\times CA\times PQ \\ PC\times AR &= CA\times PQ \\ 5\sqrt{6}\times AR &= 10\sqrt{2}\times 10 \\ AR &= \frac{100\sqrt{2}}{5\sqrt{6}} \\ &= \frac{20}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ AR &= \frac{20}{3}\sqrt{3} \end{align}$
Jadi, jarak titik A ke bidang CFH adalah $\frac{20}{3}\sqrt{3}$ cm.
Cara alternatif:
Jarak titik A ke bidang CFH pada kubus ABCD.EFGH adalah $\frac{2}{3}s\sqrt{3}=\frac{2}{3}.10\sqrt{3}=\frac{20}{3}\sqrt{3}$.
Jawaban: D
Soal No. 4
Diketahui bidang empat T.ABC dengan AT, AB dan AC saling tegak lurus di A. Jika panjang AB = AC = AT = 5 cm, maka jarak titik A ke bidang TBC adalah … cm.(A) $\frac{5}{4}\sqrt{6}$
(B) $\frac{5}{3}\sqrt{3}$
(C) $\frac{5}{2}\sqrt{2}$
(D) $\frac{5}{3}\sqrt{6}$
(E) $5\sqrt{2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar!
Jarak titik A ke bidang TBC adalah:
= jarak titik A ke garis TD
= jarak titik A ke titik E
= panjang ruas garis AE
Perhatikan segitiga BAC siku-siku di A maka $AD=\frac{5}{2}\sqrt{2}$.
Perhatikan segitiga TAD, siku-siku di A maka:
$\begin{align}TD &= \sqrt{AT^2+AD^2} \\ &= \sqrt{5^2+\left( \frac{5}{2}\sqrt{2} \right)^2} \\ &= \sqrt{25+\frac{25}{2}} \\ &= \sqrt{\frac{75}{2}} \\ &= \frac{5\sqrt{3}}{\sqrt{2}} \\ TD &= \frac{5}{2}\sqrt{6} \end{align}$
$\begin{align}AE &= \frac{AT\times AD}{TD} \\ &= \frac{5\times \frac{5}{2}\sqrt{2}}{\frac{5}{2}\sqrt{6}} \\ &= \frac{5}{\sqrt{3}} \\ AE &= \frac{5}{3}\sqrt{3} \end{align}$
Jadi, jarak titik A ke bidang TBC adalah $\frac{5}{3}\sqrt{3}$ cm.
Cara alternatif:
Perhatikan $AT\bot AB\bot AC$ maka jarak titik A ke bidang TBC adalah:
= $\frac{1}{\sqrt{\frac{1}{AT^2}+\frac{1}{AB^2}+\frac{1}{AC^2}}}$
= $\frac{1}{\sqrt{\frac{1}{5^2}+\frac{1}{5^2}+\frac{1}{5^2}}}$
= $\frac{1}{\frac{\sqrt{3}}{5}}$
= $\frac{5}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
= $\frac{5}{3}\sqrt{3}$
Jawaban: B
Soal No. 5
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm. Jika P, Q, dan R masing-masing pertengahan FG, CG, dan HG, maka jarak titik G ke segitiga PQR adalah ... cm.(A) $\frac{9}{2}\sqrt{6}$
(B) $\frac{9}{2}\sqrt{2}$
(C) $2\sqrt{3}$
(D) $\sqrt{6}$
(E) $4\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik G ke bidang PQR adalah:
= Jarak titik G ke garis QS
= Jarak titik G ke titik T
= GT
GE adalah diagonal sisi kubus maka:
$GE=s\sqrt{2}=12\sqrt{2}$
Perhatikan segitiga RGP, luasnya adalah:
$\begin{align}\frac{1}{2}\times PR\times GS &= \frac{1}{2}\times GP\times GR \\ GS &= \frac{GP\times GR}{PR} \\ &= \frac{6\times 6}{6\sqrt{2}} \\ GS &= 3\sqrt{2} \end{align}$
Segitiga QGS siku-siku di titik G maka:
$\begin{align}QS &= \sqrt{GQ^2+GS^2} \\ &= \sqrt{6^2+\left( 3\sqrt{2} \right)^2} \\ &= \sqrt{54} \\ QS &= 3\sqrt{6} \end{align}$
Luas segitiga QGS adalah:
$\begin{align}\frac{1}{2}\times QS\times GT &= \frac{1}{2}\times GQ\times GS \\ QS\times GT &= GQ\times GS \\ 3\sqrt{6}\times GT &= 6\times 3\sqrt{2} \\ GT &= \frac{18\sqrt{2}}{3\sqrt{6}} \\ &= \frac{6}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ GT &= 2\sqrt{3} \end{align}$
Jadi, jarak titik G ke bidang PQR adalah $2\sqrt{3}$ cm.
Cara alternatif:
Perhatikan bahwa $GP\bot GQ\bot GR$ maka jarak titik G ke bidang PQR adalah:
= $\frac{1}{\sqrt{\frac{1}{GP^2}+\frac{1}{GR^2}+\frac{1}{GQ^2}}}$
= $\frac{1}{\sqrt{\frac{1}{6^2}+\frac{1}{6^2}+\frac{1}{6^2}}}$
= $\frac{1}{\sqrt{\frac{3}{36}}}$
= $\frac{1}{\frac{\sqrt{3}}{6}}$
= $\frac{6}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
= $2\sqrt{3}$
Jawaban: C
Soal No. 6
SIMAK UI 2009 Kode 944. Pada bidang empat T.ABC diketahui ABC segitiga sama sisi, rusuk TA tegak lurus bidang alas. Jika panjang rusuk alas 10 cm, dan tinggi limas 15 cm, maka jarak titik A ke bidang TBC adalah ...(A) 5 cm
(B) 5,5 cm
(C) 7,5 cm
(D) $5\sqrt{3}$ cm
(E) $10\sqrt{3}$ cm
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik A ke bidang TBC adalah:
= jarak titik A ke garis TD
= jarak titik A ke titik E
= panjang ruas garis AE
ABC segitiga sama sisi maka:
AD garis tinggi membagi dua sisi BC.
$\begin{align}AD &= \sqrt{AB^2-BD^2} \\ &= \sqrt{10^2-5^2} \\ &= \sqrt{75} \\ AD &= 5\sqrt{3} \end{align}$
Perhatikan segitiga TAD, siku-siku di A maka:
$\begin{align}TD &= \sqrt{AT^2+AD^2} \\ &= \sqrt{15^2+\left( 5\sqrt{3} \right)^2} \\ &= \sqrt{300} \\ TD &= 10\sqrt{3} \end{align}$
Luas segitiga TAD:
$\begin{align}\frac{1}{2}\times TD\times AE &= \frac{1}{2}\times AD\times AT \\ TD\times AE &= AD\times AT \\ 10\sqrt{3}\times AE &= 5\sqrt{3}\times 15 \\ AE &= 7,5 \end{align}$
Jadi, jarak titik A ke bidang TBC adalah 7,5 cm.
Jawaban: C
Soal No. 7
Diketahui limas beraturan T.ABCD dengan panjang rusuk 6 cm. Titik P pada CT sehingga TP:PC = 2:1. Jarak titik P ke bidang BDT adalah ... cm.(A) 1
(B) 2
(C) $\sqrt{2}$
(D) $\sqrt{3}$
(E) $2\sqrt{2}$
Penyelesaian: Lihat/Tutup
TP:PC = 2:1 maka dapat kita misalkan TP = 2a dan PC = a$\begin{align}TP+PC &= TC \\ 2a+a &= 6 \\ 3a &= 6 \\ a &= 2 \end{align}$
Maka TP = 4 cm dan PC = 2 cm.
Perhatikan gambar berikut!

Jarak titik P ke bidang BDT
= jarak titik P ke garis TO
= jarak titik P ke titik Q
= PQ
Segitiga ABC siku-siku di titik B maka:
$\begin{align}AC &= \sqrt{AB^2+BC^2} \\ &= \sqrt{6^2+6^2} \\ AC &= 6\sqrt{2} \end{align}$
$OC=\frac{1}{2}AC=3\sqrt{2}$
Segitiga TOC sebangun dengan segitiga TQP maka perbandingan sisinya adalah:
$\begin{align}\frac{PQ}{CO} &= \frac{TP}{TC} \\ \frac{PQ}{3\sqrt{2}} &= \frac{4}{6} \\ PQ &= 2\sqrt{2} \end{align}$
Jadi, jarak titik P ke bidang BDT adalah $2\sqrt{2}$ cm.
Jawaban: E
Soal No. 8
Diketahui kubus ABCD.EFGH dengan panjang rusuk 2 cm. Titik M berada di tengah ruas garis EH. Titik N berada ditengah ruas garis EF. Jarak titik E ke bidang MNA adalah ... cm.(A) 1
(B) 2/3
(C) 1/2
(D) 3/4
(E) 1/4
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik E ke bidang MNA adalah:
= Jarak titik E ke garis AP
= Jarak titik E ke titik Q
= EQ
Perhatikan segitiga MEN;
$\begin{align}EP &= \frac{EM\times EN}{MN} \\ &= \frac{1\times 1}{\sqrt{2}} \\ EP &= \frac{1}{2}\sqrt{2} \end{align}$
Segitiga AEP siku-siku di titik E maka:
$\begin{align}AP &= \sqrt{AE^2+EP^2} \\ &= \sqrt{2^2+\left( \frac{1}{2}\sqrt{2} \right)^2} \\ &= \sqrt{\frac{9}{2}} \\ &= \frac{3}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ AP &= \frac{3}{2}\sqrt{2} \end{align}$
Luas segitiga AEP adalah:
$\begin{align}\frac{1}{2}\times AP\times EQ &= \frac{1}{2}\times EP\times AE \\ EQ &= \frac{EP\times AE}{AP} \\ &= \frac{\frac{1}{2}\sqrt{2}\times 2}{\frac{3}{2}\sqrt{2}} \\ EQ &= \frac{2}{3} \end{align}$
Jadi, jarak titik E ke bidang MNA adalah 2/3 cm.
Cara alternatif:
$EA\bot EM\bot EN$ maka jarak titik E ke bidang MNA adalah:
= $\frac{1}{\sqrt{\frac{1}{EA^2}+\frac{1}{EM^2}+\frac{1}{EN^2}}}$
= $\frac{1}{\sqrt{\frac{1}{2^2}+\frac{1}{1^2}+\frac{1}{1^2}}}$
= $\frac{1}{\sqrt{\frac{9}{4}}}$
= $\frac{2}{3}$
Jawaban: B
Soal No. 9
Diketahui kubus ABCD.EFGH dengan panjang rusuk $2\sqrt{3}$. Jika titik P terletak pada BC dan titik Q terletak pada FG dengan BP = FQ = 2, maka jarak titik H ke bidang APQE adalah ...(A) $\sqrt{3}$
(B) 3
(C) 4
(D) $2\sqrt{5}$
(E) $2\sqrt{7}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik H ke bidang APQE adalah:
= Jarak titik H ke garis EQ
= Jarak titik H ke titik R
= HR
Luas EHQ = $\frac{1}{2}\times 2\sqrt{3}\times 2\sqrt{3}$ = 6
Segitiga EFQ siku-siku di titik F maka:
$\begin{align}EQ &= \sqrt{EF^2+FQ^2} \\ &= \sqrt{\left( 2\sqrt{3} \right)^2+2^2} \\ EQ &= 4 \end{align}$
Perhatikan segitiga EHQ
$\begin{align}\text{Luas}\,\text{EHQ} &= \frac{1}{2}\times EQ\times HR \\ 6 &= \frac{1}{2}\times 4\times HR \\ 3 &= HR \end{align}$
Jadi, jarak titik H ke bidang APQE adalah 3 cm.
Jawaban: B
Soal No. 10
Panjang rusuk sebuah kubus ABCD.EFGH adalah s cm. Jarak titik A ke bidang BED adalah ... cm.(A) $2s\sqrt{3}$
(B) $3s\sqrt{3}$
(C) $3\sqrt{s}$
(D) $\frac{1}{2}s\sqrt{3}$
(E) $\frac{1}{3}s\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik A ke bidang BED adalah:
= Jarak titik A ke garis PE
= Jarak titik A ke titik Q
= AQ
AC adalah diagonal kubus maka:
$AC=s\sqrt{2}$
$AP=\frac{1}{2}AC=\frac{1}{2}s\sqrt{2}$
Segitiga EAP siku-siku di titik E maka:
$\begin{align}PE &= \sqrt{AP^2+AE^2} \\ &= \sqrt{\left( \frac{1}{2}s\sqrt{2} \right)^2+s^2} \\ &= \sqrt{\frac{6s^2}{4}} \\ PE &= \frac{1}{2}s\sqrt{6} \end{align}$
Luas segitiga EAP:
$\begin{align}\frac{1}{2}\times PE\times AQ &= \frac{1}{2}\times AP\times AE \\ AQ &= \frac{AP\times AE}{PE} \\ &= \frac{\frac{1}{2}s\sqrt{2}\times s}{\frac{1}{2}s\sqrt{6}} \\ &= \frac{s}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ AQ &= \frac{1}{3}s\sqrt{3} \end{align}$
Jadi, jarak titik A ke bidang BED adalah $\frac{1}{3}s\sqrt{3}$ cm.
Cara alternatif:
$AB\bot AE\bot AD$ maka jarak titik A ke BED adalah:
= $\frac{1}{\sqrt{\frac{1}{AB^2}+\frac{1}{AE^2}+\frac{1}{AD^2}}}$
= $\frac{1}{\sqrt{\frac{1}{s^2}+\frac{1}{s^2}+\frac{1}{s^2}}}$
= $\frac{1}{\sqrt{\frac{3}{{{s}^{2}}}}}$
= $\frac{s}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
= $\frac{1}{3}s\sqrt{3}$
Jawaban: E
Soal No. 11
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Jarak titik C ke bidang BDG adalah ... cm.(A) $\frac{4}{3}\sqrt{3}$
(B) $\frac{3}{4}\sqrt{3}$
(C) $\frac{4}{3}\sqrt{2}$
(D) $\frac{3}{4}\sqrt{2}$
(E) $\frac{8}{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik C ke bidang BDG adalah:
= Jarak titik C ke garis PC
= Jarak titik C ke titik Q
= CQ
AC adalah diagonal sisi kubus maka:
$AC=s\sqrt{2}=4\sqrt{2}$
$PC=\frac{1}{2}AC=2\sqrt{2}$
Segitiga PCG siku-siku di titik C maka:
$\begin{align}PG &= \sqrt{PC^2+CG^2} \\ &= \sqrt{\left( 2\sqrt{2} \right)^2+4^2} \\ &= \sqrt{24} \\ PG &= 2\sqrt{6} \end{align}$
Luas segitiga PCG adalah:
$\begin{align}\frac{1}{2}\times PG\times CQ &= \frac{1}{2}\times PC\times CG \\ CQ &= \frac{PC\times CG}{PG} \\ &= \frac{2\sqrt{2}\times 4}{2\sqrt{6}} \\ &= \frac{4}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ CQ &= \frac{4}{3}\sqrt{3} \end{align}$
Jadi, jarak titik C ke bidang BDG adalah $\frac{4}{3}\sqrt{3}$ cm.
Cara alternatif:
$CB\bot CD\bot CG$ maka jarak titik C ke bidang BDG adalah:
= $\frac{1}{\sqrt{\frac{1}{CB^2}+\frac{1}{CD^2}+\frac{1}{CG^2}}}$
= $\frac{1}{\sqrt{\frac{1}{4^2}+\frac{1}{4^2}+\frac{1}{4^2}}}$
= $\frac{1}{\sqrt{\frac{3}{16}}}$
= $\frac{4}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}$
= $\frac{4}{3}\sqrt{3}$
Jawaban: A
Soal No. 12
Diketahui kubus ABCD.EFGH dengan panjang rusuk 2 cm. Jika P titik tengah AE, Q titik tengah BF, titik R pada BC dan titik S pada AD sehingga BR = AS = $\sqrt{3}$ cm, maka jarak dari titik A ke bidang PQRS adalah ... cm.(A) $\frac{1}{2}\sqrt{2}$
(B) $\frac{1}{2}\sqrt{3}$
(C) 1
(D) $\sqrt{2}$
(E) $\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik A ke bidang PQRS adalah:
= Jarak titik A ke garis PS
= Jarak titik A ke titik T
= AT
Segitiga PAS siku-siku di titik A maka:
$\begin{align}PS &= \sqrt{AS^2+AP^2} \\ &= \sqrt{\left( \sqrt{3} \right)^2+1^2} \\ PS &= 2 \end{align}$
Luas segitiga PAS adalah:
$\begin{align}\frac{1}{2}\times PS\times AT &= \frac{1}{2}\times AS\times AP \\ AT &= \frac{AS\times AP}{PS} \\ &= \frac{\sqrt{3}\times 1}{2} \\ AT &= \frac{1}{2}\sqrt{3} \end{align}$
Jawaban: B
Soal No. 13
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik F ke bidang ACH adalah ... cm.(A) $8\sqrt{3}$
(B) $\frac{16}{3}\sqrt{3}$
(C) $8\sqrt{2}$
(D) $\frac{16}{3}\sqrt{2}$
(E) $8\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik F ke bidang ACH adalah:
= Jarak titik F ke garis PH
= Jarak titik F ke titik R
= FR
HF adalah diagonal sisi kubus, maka:
$HF=s\sqrt{2}=8\sqrt{2}$
Luas segitiga HPF = $\frac{1}{2}\times 8\sqrt{2}\times 8$ = $32\sqrt{2}$.
BD adalah diagonal sisi kubus maka:
$BD=s\sqrt{2}=8\sqrt{2}$
$DP=\frac{1}{2}BD=4\sqrt{2}$
Segitiga HDP siku-siku di titik D maka:
= $\begin{align}PH &= \sqrt{DP^2+DH^2} \\ &= \sqrt{\left( 4\sqrt{2} \right)^2+8^2} \\ &= \sqrt{96} \\ PH &= 4\sqrt{6} \end{align}$
$\begin{align}Luas\,HPE &= \frac{1}{2}\times PH\times FR \\ 32\sqrt{2} &= \frac{1}{2}\times 4\sqrt{6}\times FR \\ FR &= \frac{16}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ FR &= \frac{16}{3}\sqrt{3} \end{align}$
Jadi, jarak titik F ke bidang ACH adalah $\frac{16}{3}\sqrt{3}$ cm.
Jawaban: B
Soal No. 14
Diketahui limas segi empat beraturan T.ABCD dengan panjang rusuk sama yaitu 6 cm. Jika P titik tengah CD, maka jarak titik P ke bidang TAB adalah ... cm.(A) $2\sqrt{6}$
(B) $2\sqrt{3}$
(C) $3\sqrt{2}$
(D) $3\sqrt{6}$
(E) $3\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik P ke bidang TAB adalah:
= Jarak titik P ke garis TQ
= Jarak titik P ke titik R
= PR
segitiga AQT siku-siku di titik Q maka:
$\begin{align}TQ &= \sqrt{AT^2-AQ^2} \\ &= \sqrt{6^2-3^2} \\ &= \sqrt{27} \\ TQ &= 3\sqrt{3} \end{align}$
Segitiga TOQ siku-siku di titik O maka:
$\begin{align}TO &= \sqrt{TQ^2-OQ^2} \\ &= \sqrt{\left( 3\sqrt{3} \right)^2-3^2} \\ &= \sqrt{18} \\ TO &= 3\sqrt{2} \end{align}$
Luas segitiga TPQ adalah:
$\begin{align}\frac{1}{2}\times TQ\times PR &= \frac{1}{2}\times PQ\times TO \\ PR &= \frac{PQ\times TO}{TQ} \\ &= \frac{6\times 3\sqrt{2}}{3\sqrt{3}} \\ &= \frac{6\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ PR &= 2\sqrt{6} \end{align}$
Jadi, jarak titik P ke bidang TAB adalah $2\sqrt{6}$ cm.
Jawaban: A
Soal No. 15
Sebuah kubus ABCD.EFGH memiliki panjang rusuk 8 cm. Titik P adalah titik potong garis FH dengan garis EG, sedangkan titik Q adalah titik potong garis AC dengan garis BD. Jarak titik Q dengan bidang BCP adalah ... cm.(A) $\frac{4}{5}\sqrt{5}$
(B) $\frac{8}{5}\sqrt{5}$
(C) $\frac{4}{3}\sqrt{3}$
(D) $\frac{8}{3}\sqrt{3}$
(E) $\frac{4}{3}\sqrt{2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik Q ke bidang BCP adalah:
= Jarak titik Q ke garis PR
= Jarak titik Q ke titik S
= QS
Segitiga PQR siku-siku di titik Q maka:
$\begin{align}PR &= \sqrt{PQ^2+QR^2} \\ &= \sqrt{8^2+4^2} \\ &= \sqrt{80} \\ PR &= 4\sqrt{5} \end{align}$
Luas segitiga PQR adalah:
$\begin{align}\frac{1}{2}\times PR\times QS &= \frac{1}{2}\times QR\times PQ \\ QS &= \frac{QR\times PQ}{PR} \\ &= \frac{4\times 8}{4\sqrt{5}} \\ &= \frac{8}{\sqrt{5}}\times \frac{\sqrt{5}}{\sqrt{5}} \\ QS &= \frac{8}{5}\sqrt{5} \end{align}$
Jadi, jarak titik Q ke bidang BCP adalah $\frac{8}{5}\sqrt{5}$ cm.
Jawaban: B
Soal No. 16
Diketahui kubus ABCD.EFGH panjang rusuk kubus 12 cm. Titik P terletak pada perpanjangan rusuk DC sehingga CP:DP = 1:3. Jarak titik P dengan bidang BDHF adalah ... cm.(A) $6\sqrt{2}$
(B) $9\sqrt{2}$
(C) $12\sqrt{2}$
(D) $16\sqrt{2}$
(E) $18\sqrt{2}$
Penyelesaian: Lihat/Tutup
DC di perpanjang sehingga CP:DP = 1: 3Misal: CP = x maka DP = 3x
$\begin{align}DC &= DP-CP \\ 12 &= 3x-x \\ 12 &= 2x \\ 6 &= x \end{align}$
Jadi, panjang CP = x = 6 cm.
Perhatikan gambar berikut!

Jarak titik P ke bidang BDHF adalah:
= Jarak titik P ke garis BD
= Jarak titik P ke titik Q
= PQ
AC adalah diagonal sisi kubus maka:
$AC=s\sqrt{2}=12\sqrt{2}$
$CR=\frac{1}{2}AC=6\sqrt{2}$
Perhatikan:
Segitiga DQP sebangun dengan segitiga DRC maka perbandingan sisi-sisi yang bersesuaian adalah:
$\begin{align}\frac{PQ}{CR} &= \frac{DP}{DC} \\ PQ &= \frac{DP\times CR}{DC} \\ &= \frac{18\times 6\sqrt{2}}{12} \\ PQ &= 9\sqrt{2} \end{align}$
Jadi, jarak titik P ke bidang BDHF adalah $9\sqrt{2}$ cm.
Jawaban: B
Soal No. 17
Diketahui bidang empat T.ABC dengan AT, AB, dan AC saling tegak lurus di A. Jika panjang AB = AC = AT = $3\sqrt{2}$ cm, maka jarak A ke bidang TBC adalah ... cm.(A) $\frac{3}{4}\sqrt{6}$
(B) $\sqrt{6}$
(C) $\frac{3}{2}\sqrt{2}$
(D) $3\sqrt{6}$
(E) $9\sqrt{2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik A ke bidang TBC adalah:
= jarak titik A ke garis TD
= jarak titik A ke titik E
= panjang ruas garis AE
AD = 3 cm
Perhatikan segitiga TAD, siku-siku di A maka:
$\begin{align}TD &= \sqrt{AT^2+AD^2} \\ &= \sqrt{\left( 3\sqrt{2} \right)^2+3^2} \\ &= \sqrt{27} \\ TD &= 3\sqrt{3} \end{align}$
$\begin{align}AE &= \frac{AT\times AD}{TD} \\ &= \frac{3\sqrt{2}\times 3}{3\sqrt{3}} \\ &= \frac{3\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ AE &= \sqrt{6} \end{align}$
Jadi, jarak titik A ke bidang TBC adalah $\sqrt{6}$ cm.
Cara alternatif:
Perhatikan $AT\bot AB\bot AC$ maka jarak titik A ke bidang TBC adalah:
= $\frac{1}{\sqrt{\frac{1}{AT^2}+\frac{1}{AB^2}+\frac{1}{AC^2}}}$
= $\frac{1}{\sqrt{\frac{1}{\left( 3\sqrt{2} \right)^2}+\frac{1}{\left( 3\sqrt{2} \right)^2}+\frac{1}{\left( 3\sqrt{2} \right)^2}}}$
= $\sqrt{6}$
Jadi, jarak titik A ke bidang TBC adalah $\sqrt{6}$ cm.
Jawaban: B
Soal No. 18
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P terletak pada perpanjangan rusuk DC sehingga CP:DP = 1:3. Jarak titik P dengan BDHF adalah ... cm.(A) $6\sqrt{2}$
(B) $9\sqrt{2}$
(C) $3\sqrt{2}$
(D) $\frac{9}{2}\sqrt{2}$
(E) $12\sqrt{2}$
Penyelesaian: Lihat/Tutup
DC di perpanjang sehingga CP:DP = 1: 3Misal: CP = x maka DP = 3x
$\begin{align}DC &= DP-CP \\ 6 &= 3x-x \\ 6 &= 2x \\ 3 &= x \end{align}$
Jadi, panjang CP = x = 3 cm.
Perhatikan gambar berikut!

Jarak titik P ke bidang BDHF adalah:
= Jarak titik P ke garis BD
= Jarak titik P ke titik Q
= PQ
AC adalah diagonal sisi kubus maka:
$AC=s\sqrt{2}=6\sqrt{2}$
$CR=\frac{1}{2}AC=3\sqrt{2}$
Perhatikan:
Segitiga DQP sebangun dengan segitiga DRC maka perbandingan sisi-sisi yang bersesuaian adalah:
$\begin{align}\frac{PQ}{CR} &= \frac{DP}{DC} \\ PQ &= \frac{DP\times CR}{DC} \\ &= \frac{9\times 3\sqrt{2}}{6} \\ PQ &= \frac{9}{2}\sqrt{2} \end{align}$
Jadi, jarak titik P ke bidang BDHF adalah $\frac{9}{2}\sqrt{2}$ cm.
Jawaban: D
Soal No. 19
Diketahui ABCD.EFGH dengan luas permukaan $18a^2$ $\text{cm^2}$. Jarak titik A ke bidang CFH adalah ... cm.(A) a
(B) 2a
(C) 3a
(D) 4a
(E) 5a
Penyelesaian: Lihat/Tutup
Luas permukaan kubus = $6s^2$$\begin{align}6s^2 &= 18a^2 \\ s^2 &= 3a^2 \\ s &= a\sqrt{3} \end{align}$
Jadi, rusuk kubus ABCD.EFGH adalah $a\sqrt{3}$ cm.
Perhatikan gambar berikut!

Jarak titik A ke bidang CFH adalah:
= Jarak titik A ke garis PC
= Jarak titik A ke titik R
= AR
CA dan GE adalah diagonal kubus maka:
$CA=s\sqrt{2}=a\sqrt{3}.\sqrt{2}=a\sqrt{6}$
$GE=s\sqrt{2}=a\sqrt{3}.\sqrt{2}=a\sqrt{6}$
$GP=\frac{1}{2}GE=\frac{1}{2}a\sqrt{6}$
Segitiga CGP siku-siku di titik G maka:
$\begin{align}PC &= \sqrt{CG^2+GP^2} \\ &= \sqrt{\left( a\sqrt{3} \right)^2+\left( \frac{1}{2}a\sqrt{6} \right)^2} \\ &= \sqrt{\frac{9a^2}{2}} \\ PC &= \frac{3a}{2}\sqrt{2} \end{align}$
Perhatikan segitiga CPA:
Luas segitiga CPA:
$\begin{align}\frac{1}{2}\times PC\times AR &= \frac{1}{2}\times CA\times PQ \\ AR &= \frac{CA\times PQ}{PC} \\ &= \frac{a\sqrt{6}\times a\sqrt{3}}{\frac{3a}{2}\sqrt{2}} \\ AR &= 2a \end{align}$
Jadi, jarak titik A ke bidang CFH adalah $2a$ cm.
Cara alternatif:
Jarak titik A ke bidang CFH pada kubus ABCD.EFGH adalah $\frac{2}{3}s\sqrt{3}=\frac{2}{3}.a\sqrt{3.}\sqrt{3}=2a$.
Jawaban: B
Soal No. 20
Diketahui balok ABCD.EFGH memiliki rusuk AB = AD = 12 cm dan AE = 24 cm. Jarak titik G ke bidang BDE adalah ... cm.(A) $18\sqrt{2}$
(B) $12\sqrt{2}$
(C) 16
(D) 12
(E) $6\sqrt{2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik G ke bidang BDE adalah:
= Jarak titik G ke garis PE
= Jarak titik G ke titik Q
= GQ
Perhatikan segitiga ABC:
$\begin{align}AC &= \sqrt{AB^2+BC^2} \\ &= \sqrt{12^2+12^2} \\ AC &= 12\sqrt{2} \end{align}$
$AP=\frac{1}{2}AC=6\sqrt{2}$
Perhatikan segitiga EAP:
$\begin{align}PE &= \sqrt{AE^2+AP^2} \\ &= \sqrt{24^2+\left( 6\sqrt{2} \right)^2} \\ &= \sqrt{576+72} \\ &= \sqrt{648} \\ PE &= 18\sqrt{2} \end{align}$
Luas segitiga PEG adalah:
$\begin{align}\frac{1}{2}\times PE\times GQ &= \frac{1}{2}\times EG\times PR \\ GQ &= \frac{EG\times PR}{PE} \\ &= \frac{12\sqrt{2}\times 24}{18\sqrt{2}} \\ GQ &= 16 \end{align}$
Jadi, jarak titik G ke bidang BDE adalah 16 cm.
Jawaban: C

Post a Comment for "Soal Jarak Titik ke Bidang pada Dimensi Tiga dan Pembahasan"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.