Soal Jarak Titik ke Garis pada Dimensi Tiga dan Pembahasan
Berikut ini adalah Kumpulan Soal Jarak Titik ke Garis pada Dimensi Tiga dan Pembahasannya. Bagi adik-adik silahkan dipelajari dan jangan lupa share/bagikan ke media sosial kalian, agar manfaat postingan ini dapat dirasakan oleh siswa/i yang lain. Terima kasih.
(A) $3\sqrt{5}$
(B) $5\sqrt{2}$
(C) $5\sqrt{6}$
(D) $10\sqrt{2}$
(E) $10\sqrt{6}$

Dari gambar, jarak titik F ke garis AC adalah jarak titik F ke titik Q yaitu panjang ruas garis FQ.
Perhatikan segitiga ACF,
AC = CF = AF = $10\sqrt{2}$ (diagonal sisi kubus).
Karena AF = CF maka garis tinggi FQ membagi dua sama panjang garis AC, sehingga diperoleh:
$\begin{align}AQ &= \frac{1}{2}AC \\ &= \frac{1}{2}.10\sqrt{2} \\ AQ &= 5\sqrt{2} \end{align}$
Pada segitiga AQF siku-siku di Q maka:
$\begin{align}FQ &= \sqrt{AF^2-AQ^2} \\ &= \sqrt{(10\sqrt{2})^2-(5\sqrt{2})^2} \\ &= \sqrt{200-50} \\ &= \sqrt{150} \\ FQ &= 5\sqrt{6} \end{align}$
Jadi, jarak titik F ke garis AC adalah $5\sqrt{6}$ cm.
Jawaban: C
(A) $3\sqrt{5}$
(B) $2\sqrt{6}$
(C) $\sqrt{6}$
(D) $2\sqrt{3}$
(E) $\sqrt{3}$

Jarak titik H ke garis DF adalah panjang ruas garis HP.
HF adalah diagonal sisi kubus, maka:
$HF=s\sqrt{2}=6\sqrt{2}$
DF adalah diagonal ruang kubus, maka:
$DF=s\sqrt{3}=6\sqrt{3}$
Perhatikan segitiga DHF, dengan menggunakan rumus luas segitiga maka:
$\begin{align}\frac{1}{2}.DF.HP &= \frac{1}{2}.HD.HF \\ HP &= \frac{HD.HF}{DF} \\ &= \frac{6\times 6\sqrt{2}}{6\sqrt{3}} \\ &= \frac{6\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ HP &= 2\sqrt{6} \end{align}$
Cara alternatif:
Jarak titik sudut kubus (titik H) ke diagonal ruang kubus (garis DF) adalah $\frac{s}{3}\sqrt{6} = \frac{6}{3}\sqrt{6} = 2\sqrt{6}$.
Jawaban: B
(A) 6
(B) $6\sqrt{2}$
(C) $6\sqrt{3}$
(D) $6\sqrt{6}$
(E) 12

Jarak titik M ke garis EG adalah panjang ruas garis MP.
Perhatikan segitiga EBM.
BE adalah diagonal sisi kubus, maka:
$BE=s\sqrt{2}=8\sqrt{2}$
$\begin{align}EM &= \sqrt{BE^2+BM^2} \\ &= \sqrt{(8\sqrt{2})^2+4^2} \\ &= \sqrt{128+16} \\ &= \sqrt{144} \\ EM &= 12 \end{align}$
Perhatikan segitiga MCG.
$\begin{align}GM &= \sqrt{CM^2+CG^2} \\ &= \sqrt{4^2+8^2} \\ &= \sqrt{16+64} \\ &= \sqrt{80} \\ GM &= 4\sqrt{5} \end{align}$
Perhatikan segitiga MEG, dengan menggunakan aturan cosinus maka:
$\begin{align}\cos \angle MEG &= \frac{EG^2+EM^2-GM^2}{2.EG.EM} \\ &= \frac{(8\sqrt{2}^2+12^2-(4\sqrt{5})^2}{2.8\sqrt{2}.12} \\ &= \frac{128+144-80}{192\sqrt{2}} \\ &= \frac{192}{192\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ \cos \angle MEG &= \frac{1}{2}\sqrt{2} \\ \angle MEG &= 45^\circ \end{align}$
Perhatikan segitiga MEG, dengan menggunakan rumus luas segitiga maka:
$\begin{align}\frac{1}{2}.EG.MP &= \frac{1}{2}.EG.EM.\sin \angle MEG \\ MP &= EM.\sin 45^\circ \\ MP &= 12.\frac{1}{2}\sqrt{2} \\ MP &= 6\sqrt{2} \end{align}$
Jawaban: B
(A) $\frac{1}{2}$
(B) $\frac{1}{3}\sqrt{3}$
(C) $\frac{1}{2}\sqrt{3}$
(D) 1
(E) $\frac{2}{3}\sqrt{3}$
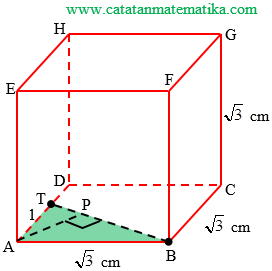
Perhatikan segitiga TAB, siku-siku di A maka:
$\begin{align}BT &= \sqrt{AB^2+AT^2} \\ &= \sqrt{(\sqrt{3})^2+1^2} \\ BT &= 2 \end{align}$
Jarak titik A ke garis BT adalah panjang AP.
$\begin{align}AP &= \frac{AB\times AT}{BT} \\ &= \frac{\sqrt{3}\times 1}{2} \\ AP &= \frac{1}{2}\sqrt{3} \end{align}$
Jawaban: C
(A) $2\sqrt{2}$
(B) $2\sqrt{3}$
(C) $3\sqrt{2}$
(D) $3\sqrt{3}$
(E) $2\sqrt{5}$
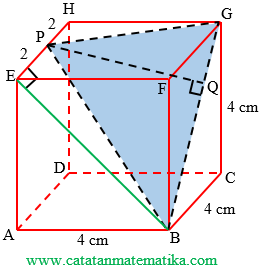
Jarak titik P ke garis BG adalah panjang ruas garis PQ.
Perhatikan segitiga BEP, siku-siku di titik E.
BE adalah diagonal sisi kubus, maka:
$BE=s\sqrt{2}=4\sqrt{2}$
$\begin{align}BP &= \sqrt{BE^2+EP^2} \\ &= \sqrt{(4\sqrt{2})^2+2^2} \\ &= \sqrt{32+4} \\ &= \sqrt{36} \\ BP &= 6 \end{align}$
Perhatikan segitiga PHG, siku-siku di titik H.
$\begin{align}PG &= \sqrt{HP^2+HG^2} \\ &= \sqrt{2^2+4^2} \\ &= \sqrt{20} \\ PG &= 2\sqrt{5} \end{align}$
BG adalah diagonal sisi kubus, maka:
$BG=s\sqrt{2}=4\sqrt{2}$
Perhatikan segitiga BGP:
Arutan cosinus:
$\begin{align}\cos \angle BGP &= \frac{BG^2+GP^2-BP^2}{2.BG.GP} \\ &= \frac{(4\sqrt{2})^2+(2\sqrt{5})^2-6^2}{2.4\sqrt{2}.2\sqrt{5}} \\ &= \frac{32+20-36}{16\sqrt{10}} \\ &= \frac{16}{16\sqrt{10}} \\ \cos \angle BGP &= \frac{1}{\sqrt{10}} \end{align}$
$\sin \angle BGP = \frac{\sqrt{(\sqrt{10})^2-1^2}}{\sqrt{10}} = \frac{3}{\sqrt{10}}$
Dengan menggunakan luas segitiga BPG maka:
$\begin{align}\frac{1}{2}.BG.PQ &= \frac{1}{2}.GB.GP.\sin \angle BGP \\ PQ &= GP.\sin \angle BGP \\ &= 2\sqrt{5}.\frac{3}{\sqrt{10}} \\ &= \frac{6}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ PQ &= 3\sqrt{2} \end{align}$
Jawaban: C
(A) $\sqrt{6}$
(B) $2\sqrt{3}$
(C) $2\sqrt{6}$
(D) $4\sqrt{3}$
(E) $4\sqrt{6}$

Jarak titik G ke garis AP adalah panjang ruas garis GQ.
AH adalah diagonal sisi kubus, maka:
$AH=s\sqrt{2}=6\sqrt{2}$
$\begin{align}AP &= \sqrt{AH^2+HP^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+12^2} \\ &= \sqrt{72+144} \\ &= \sqrt{216} \\ AP &= 6\sqrt{6} \end{align}$
Segitiga AHP sebangun dengan segitiga GQP, maka perbandingan sisi-sisi yang bersesuaian adalah:
$\begin{align}\frac{GQ}{AH} &= \frac{GP}{AP} \\ \frac{GQ}{6\sqrt{2}} &= \frac{6}{6\sqrt{3}} \\ GQ &= \frac{6\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ GQ &= 2\sqrt{6} \end{align}$
Jawaban: C
(A) $\frac{5}{3}\sqrt{6}$
(B) $\frac{4}{3}\sqrt{6}$
(C) $\sqrt{6}$
(D) $\frac{2}{3}\sqrt{6}$
(E) $\frac{1}{3}\sqrt{6}$

Jarak titik G ke garis HB adalah panjang ruas garis GP.
Perhatikan segitiga BCG siku-siku di titik C, maka:
$\begin{align}BG &= \sqrt{BC^2+CG^2} \\ &= \sqrt{5^2+5^2} \\ &= \sqrt{50} \\ BG &= 5\sqrt{2} \end{align}$
Perhatikan segitiga BGH siku-siku di titik G, maka:
$\begin{align}HB &= \sqrt{BG^2+GH^2} \\ &= \sqrt{\left( 5\sqrt{2} \right)^2+5^2} \\ &= \sqrt{50+25} \\ &= \sqrt{75} \\ HB &= 5\sqrt{3} \end{align}$
Luas segitiga BGH:
$\begin{align}\frac{1}{2}.HB.GP &= \frac{1}{2}.HG.BG \\ HB.GP &= HG.BG \\ 5\sqrt{3}.GP &= 5.5\sqrt{2} \\ GP &= \frac{5\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ GP &= \frac{5}{3}\sqrt{6} \end{align}$
Jadi, jarak titik G ke garis HB adalah $\frac{5}{3}\sqrt{6}$ cm.
Jawaban: A
(A) $5\sqrt{6}$
(B) $4\sqrt{6}$
(C) $3\sqrt{6}$
(D) $2\sqrt{6}$
(E) $\sqrt{2}$
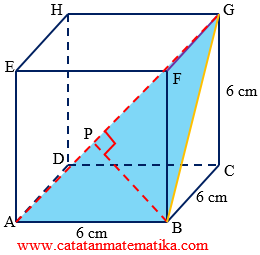
Jarak titik B ke garis AG adalah panjang ruas garis BP.
Perhatikan segitiga BCG siku-siku di titik C, maka:
$\begin{align}BG^2 &= BC^2+CG^2 \\ &= 6^2+6^2 \\ BG^2=72 \end{align}$
Perhatikan segitiga ABG siku-siku di titik B, maka:
$\begin{align}AG &= \sqrt{AB^2+BG^2} \\ &= \sqrt{6^2+\left( 6\sqrt{2} \right)^2} \\ &= \sqrt{36+72} \\ &= \sqrt{108} \\ AG &= 6\sqrt{3} \end{align}$
Luas segitiga ABG:
$\begin{align}\frac{1}{2}.AG.BP &= \frac{1}{2}.AB.BG \\ AG.BP &= AB.BG \\ 6\sqrt{3}.BP &= 6.6\sqrt{2} \\ BP &= \frac{6\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ BP &= 2\sqrt{6} \end{align}$
Jawaban: D
(A) $6\sqrt{6}$
(B) $2\sqrt{10}$
(C) $2\sqrt{11}$
(D) $4\sqrt{3}$
(E) $2\sqrt{13}$

Jarak titik A ke garis TC adalah panjang ruas garis AK.
perhatikan segitiga ABC siku-siku di titik C maka:
$\begin{align}AC &= \sqrt{AB^2+BC^2} \\ &= \sqrt{12^2+12^2} \\ &= \sqrt{{{2.12}^{2}}} \\ AC &= 12\sqrt{2} \end{align}$
Perhatikan segitiga TAC:
AT = $12\sqrt{2}$, $AC=12\sqrt{3}$
Karena AT = AC dan AK adalah garis tinggi terhadap TC, maka AK membagi dua sama panjang garis TC sehingga kita peroleh:
$\begin{align}CK &= \frac{1}{2}TC \\ &= \frac{1}{2}.12\sqrt{2} \\ CK &= 6\sqrt{2} \end{align}$
Perhatikan segitiga AKC siku-siku di titik K maka berlaku pythagoras:
$\begin{align}AK &= \sqrt{AC^2-CK^2} \\ &= \sqrt{\left( 12\sqrt{2} \right)^2-\left( 6\sqrt{2} \right)^2} \\ &= \sqrt{288-72} \\ &= \sqrt{216} \\ AK &= 6\sqrt{6} \end{align}$
Jadi, jarak titik A ke garis TC adalah $6\sqrt{6}$ cm.
Jawaban: A
(A) 6
(B) $6\sqrt{2}$
(C) $6\sqrt{3}$
(D) $6\sqrt{6}$
(E) $4\sqrt{2}$

Jarak titik A ke garis DP adalah panjang ruas garis AQ.
AF adalah diagonal sisi kubus maka:
$AF=s\sqrt{2}=6\sqrt{2}$
Perhatikan segitiga PRD siku-siku di titik R maka:
$PR=AF=6\sqrt{2}$
$\begin{align}PD &= \sqrt{PR^2+RD^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+3^2} \\ &= \sqrt{72+9} \\ &= \sqrt{81} \\ PD &= 9 \end{align}$
Perhatikan segitiga APD, maka luas segitiga APD:
$\begin{align}\frac{1}{2}.PD.AQ &= \frac{1}{2}.AD.PR \\ PD.AQ &= AD.PR \\ 9.AD &= 6.9 \\ AD &= 6 \end{align}$
Jawaban: A
(A) $\sqrt{10}$
(B) $3\sqrt{5}$
(C) $\frac{9}{5}$
(D) $3\sqrt{2}$
(E) 3

Jarak titik R ke garis BT adalah panjang ruas garis PR.
Segitiga BCR siku-siku di titik C, maka:
$\begin{align}BR &= \sqrt{BC^2+CR^2} \\ &= \sqrt{6^2+3^2} \\ &= \sqrt{36+9} \\ &= \sqrt{45} \\ BR &= 3\sqrt{5} \end{align}$
Segitiga RGT siku-siku di titik G, maka:
$\begin{align}RT &= \sqrt{RG^2+GT^2} \\ &= \sqrt{3^2+3^2} \\ &= \sqrt{18} \\ RT &= 3\sqrt{2} \end{align}$
BG diagonal sisi kubus, maka $BG=6\sqrt{2}$.
Segitiga BGT siku-siku di titik G, maka:
$\begin{align}BT &= \sqrt{BG^2+GT^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+3^2} \\ &= \sqrt{72+9} \\ &= \sqrt{81} \\ BT &= 9 \end{align}$
Pada segitiga BRT, berlaku aturan cosinus sebagai berikut:
$\begin{align}\cos \angle RBT &= \frac{BR^2+BT^2-RT^2}{2.BR.BT} \\ &= \frac{\left( 3\sqrt{5} \right)^2+9^2-\left( 3\sqrt{2} \right)^2}{2.3\sqrt{5}.9} \\ &= \frac{45+81-18}{54\sqrt{5}} \\ &= \frac{108}{54\sqrt{5}} \\ \cos \angle RBT &= \frac{2}{\sqrt{5}} \end{align}$
Dengan perbandingan trigonometri diperoleh:
$\sin \angle RBT = \frac{\sqrt{(\sqrt{5})^2-2^2}}{\sqrt{5}} = \frac{1}{\sqrt{5}}$
Luas segitiga RBT:
$\begin{align}\frac{1}{2}.BT.PR &= \frac{1}{2}.BT.BR.\sin \angle RBT \\ PR &= BR.\sin \angle RBT \\ PR &= 3\sqrt{5}.\frac{1}{\sqrt{5}} \\ PR &= 3 \end{align}$
Jadi, jarak titik R ke BT adalah 3 cm.
Jawaban: E
(A) $\frac{5}{2}\sqrt{3}$
(B) $\frac{5}{2}\sqrt{6}$
(C) $5\sqrt{3}$
(D) $128\sqrt{3}$
(E) $3\sqrt{2}$

Jarak titik B ke diagonal EG adalah panjang ruas garis BP.
BE, BG, dan EG adalah diagonal sisi kubus maka:
BE = BG = EG = $s\sqrt{2}=5\sqrt{2}$
Karena BE = BG dan BP adalah garis tinggi terhadap sisi EG maka BP membagi dua sama panjang garis EG sehingga diperoleh:
$\begin{align}EP &= \frac{1}{2}EG \\ &= \frac{1}{2}.5\sqrt{2} \\ EP &= \frac{5\sqrt{2}}{2} \end{align}$
Perhatikan segitiga BPE siku-siku di titik P maka:
$\begin{align}BP &= \sqrt{BE^2-EP^2} \\ &= \sqrt{\left( 5\sqrt{2} \right)^2-\left( \frac{5\sqrt{2}}{2} \right)^2} \\ &= \sqrt{50-\frac{50}{4}} \\ &= \sqrt{\frac{150}{4}} \\ &= \sqrt{\frac{25\times 6}{4}} \\ BP &= \frac{5}{2}\sqrt{6} \end{align}$
Jadi, jarak titik B ke diagonal EG adalah $\frac{5}{2}\sqrt{6}$ cm.
Jawaban: B
(A) 4
(B) $4\sqrt{2}$
(C) $4\sqrt{3}$
(D) $2\sqrt{6}$
(E) $4\sqrt{6}$

Bidang ABED tegak lurus dengan bidang BCFE.
AE terletak pada bidang ABED dan EF terletak pada bidang BCFE maka $AE\bot EF$.
Perhatikan segitiga AEF siku-siku di titik E, maka jarak titik A ke garis EF adalah panjang ruas garis AE.
Untuk menghitung panjang AE perhatikan segitiga ABD siku-siku di titik B, maka:
$\begin{align}AE &= \sqrt{AB^2+BE^2} \\ &= \sqrt{4^2+\left( 2\sqrt{2} \right)^2} \\ &= \sqrt{16+8} \\ &= \sqrt{24} \\ AE &= 2\sqrt{6} \end{align}$
Jadi, jarak titik A ke EF adalah $2\sqrt{6}$ cm.
Jawaban: D
(A) $3\sqrt{2}$
(B) $4\sqrt{2}$
(C) $6\sqrt{2}$
(D) $6\sqrt{3}$
(E) $4\sqrt{3}$

Jarak titik P ke garis AT adalah panjang ruas garis PQ.
Perhatikan segitiga TBC, karena TA = TB dan titik P membagi dua sama panjang sisi BC, maka $TP\bot BC$.
Perhatikan segitiga TPC siku-siku di titik P maka:
$\begin{align}TP &= \sqrt{TC^2-PC^2} \\ &= \sqrt{12^2-6^2} \\ &= \sqrt{144-36} \\ &= \sqrt{108} \\ TP &= 6\sqrt{3} \end{align}$
Perhatikan segitiga ABC, karena AB = AC dan titik P membagi dua sama panjang sisi BC, maka $AP\bot BC$
Perhatikan segitiga BPA siku-siku di titik P maka:
$\begin{align}AP &= \sqrt{AB^2-BP^2} \\ &= \sqrt{12^2-6^2} \\ &= \sqrt{144-36} \\ &= \sqrt{108} \\ AP &= 6\sqrt{3} \end{align}$
Perhatikan segitiga TPA, karena AP = TP dan $PQ\bot AT$ maka TQ membagi dua sama panjang garis AT sehingga kita peroleh:
$AQ=\frac{1}{2}AT=\frac{1}{2}\times 12=6$
Segitiga AQP siku-siku di titik Q maka:
$\begin{align}PQ &= \sqrt{AP^2-AQ^2} \\ &= \sqrt{\left( 6\sqrt{3} \right)^2-6^2} \\ &= \sqrt{108-36} \\ &= \sqrt{72} \\ PQ &= 6\sqrt{2} \end{align}$
Jadi, jarak titik P ke garis AT adalah $6\sqrt{2}$ cm.
Jawaban: C
(A) $\sqrt{5}$
(B) $\frac{3}{5}\sqrt{5}$
(C) $\frac{6}{5}\sqrt{5}$
(D) $\frac{3}{5}\sqrt{10}$
(E) $\frac{6}{5}\sqrt{10}$
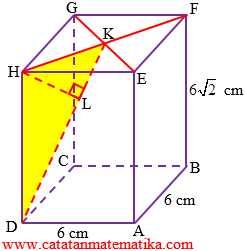
Jarak titik H ke garis DK adalah panjang ruas garis HL.
Pada segitiga HEF siku-siku di titik E maka:
$\begin{align}HF &= \sqrt{HE^2+EF^2} \\ &= \sqrt{6^2+6^2} \\ &= \sqrt{72} \\ HF &= 6\sqrt{2} \end{align}$
Titik K di tengah EG maka K juga ditengah HF.
$HK=\frac{1}{2}HF=\frac{1}{2}.6\sqrt{2}=3\sqrt{2}$
Segitiga DHK siku-siku di titik H, maka:
$\begin{align}DK &= \sqrt{HK^2+DH^2} \\ &= \sqrt{\left( 3\sqrt{2} \right)^2+\left( 6\sqrt{2} \right)^2} \\ &= \sqrt{18+72} \\ &= \sqrt{90} \\ DK &= 3\sqrt{10} \end{align}$
Luas segitiga DHK:
$\begin{align}\frac{1}{2}.DK.HL &= \frac{1}{2}.DH.HK \\ DK.HL &= DH.HK \\ 3\sqrt{10}.HL &= 6\sqrt{2}.3\sqrt{2} \\ HL &= \frac{12}{\sqrt{10}}\times \frac{\sqrt{10}}{\sqrt{10}} \\ HL &= \frac{12}{10}\sqrt{10} \\ HL &= \frac{6}{5}\sqrt{10} \end{align}$
Jadi, jarak titik H ke garis DK adalah $\frac{6}{5}\sqrt{10}$ cm.
Jawaban: E
(A) $3\sqrt{7}$
(B) $3\sqrt{6}$
(C) $3\sqrt{5}$
(D) $3\sqrt{3}$
(E) $2\sqrt{3}$

Jarak titik P ke garis QR adalah panjang ruas garis PS.
Karena PQ = PR dan $PS\bot QR$ maka PS membagi dua sama panjang garis QR.
Perhatikan, PS dan EQ terletak pada satu bidang.
EQ sejajar dengan PS, dan PS = EQ.
Perhatikan segitiga EFQ siku-siku di titik F maka:
$\begin{align}EQ &= \sqrt{EF^2+FQ^2} \\ &= \sqrt{6^2+3^2} \\ &= \sqrt{36+9} \\ &= \sqrt{45} \\ EQ &= 3\sqrt{5} \end{align}$
PS = EQ = $3\sqrt{5}$
Jadi, jarak titik P ke garis QR adalah $3\sqrt{5}$ cm.
Jawaban: C
(A) $\frac{1}{2}a\sqrt{3}$
(B) $\frac{1}{2}a\sqrt{2}$
(C) $\frac{1}{3}a\sqrt{3}$
(D) $\frac{1}{3}a\sqrt{2}$
(E) $\frac{1}{2}a\sqrt{6}$

$\begin{align}AC &= \sqrt{AB^2+BC^2} \\ &= \sqrt{\left( a\sqrt{2} \right)^2+\left( a\sqrt{2} \right)^2} \\ &= \sqrt{4a^2} \\ AC &= 2a \end{align}$
$OC=\frac{1}{2}AC=\frac{1}{2}.2a=a$
Perhatikan segitiga TOC siku-siku di titik O maka:
$\begin{align}OT &= \sqrt{TC^2-OC^2} \\ &= \sqrt{(2a)^2-a^2} \\ &= \sqrt{3a^2} \\ OT &= a\sqrt{3} \end{align}$
Luas segitiga TOC:
$\begin{align}\frac{1}{2}\times TC\times OP &= \frac{1}{2}\times OT\times OC \\ TC\times OP &= OT\times OC \\ 2a\times OP &= a\sqrt{3}\times a \\ OP &= \frac{1}{2}a\sqrt{3} \end{align}$
Jadi, jarak titik O ke garis TC adalah $\frac{1}{2}a\sqrt{3}$ cm.
Jawaban: A
(A) $4\sqrt{6}$
(B) $4\sqrt{5}$
(C) $4\sqrt{3}$
(D) $4\sqrt{2}$
(E) 4
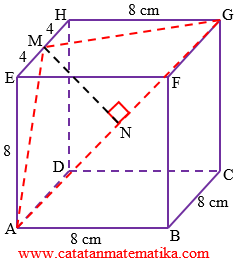
Jarak titik M ke AG adalah panjang ruas garis MN.
Perhatikan segitiga AEM siku-siku di titik E maka:
$\begin{align}AM &= \sqrt{AE^2+EM^2} \\ &= \sqrt{8^2+4^2} \\ &= \sqrt{64+16} \\ &= \sqrt{80} \\ AM &= 4\sqrt{5} \end{align}$
MG = $AM=4\sqrt{5}$
AG adalah diagonal ruang kubus, maka $AG=s\sqrt{3}=8\sqrt{3}$.
Segitiga AMG segitiga sama kaki (AM=MG), maka MN adalah garis tinggi yang membagi dua AG di titik N, maka:
$\begin{align}AN &= \frac{1}{2}.AG \\ &= \frac{1}{2}.8\sqrt{3} \\ AN &= 4\sqrt{3} \end{align}$
Segitiga ANM siku-siku di titik N maka:
$\begin{align}MN &= \sqrt{AM^2-AN^2} \\ &= \sqrt{\left( 4\sqrt{5} \right)^2-\left( 4\sqrt{3} \right)^2} \\ &= \sqrt{80-48} \\ &= \sqrt{32} \\ MN &= 4\sqrt{2} \end{align}$
Jadi, jarak titik M ke AG adalah $4\sqrt{2}$ cm.
Jawaban: D

Merupakan limas segitiga beraturan, jarak titik T ke AD adalah ...
(A) $4\sqrt{3}$
(B) $6\sqrt{3}$
(C) 11
(D) $\sqrt{133}$
(E) 12

Jarak titik T ke AD adalah panjang ruas garis TO.
Segitiga BDA siku-siku di titik D maka:
$\begin{align}AD &= \sqrt{AB^2-BD^2} \\ &= \sqrt{12^2-6^2} \\ &= \sqrt{144-36} \\ &= \sqrt{108} \\ AD &= 6\sqrt{3} \end{align}$
Segitiga TDC siku-siku di titik D maka:
$\begin{align}TD &= \sqrt{TC^2-DC^2} \\ &= \sqrt{13^2-6^2} \\ &= \sqrt{169-36} \\ TD &= \sqrt{133} \end{align}$
Dengan aturan cosinus pada segitiga TAD maka:
$\begin{align}\cos \angle TAD &= \frac{TA^2+AD^2-TD^2}{2.TA.AD} \\ &= \frac{13^2+\left( 6\sqrt{3} \right)^2-\left( \sqrt{133} \right)^2}{2.13.6\sqrt{3}} \\ &= \frac{169+108-133}{156\sqrt{3}} \\ &= \frac{144}{156\sqrt{3}} \\ \cos \angle TAD &= \frac{12}{13\sqrt{3}} \end{align}$
Dengan perbandingan trigonometri:
$\begin{align}\sin \angle TAD &= \frac{\sqrt{\left( 13\sqrt{3} \right)^2-12^2}}{13\sqrt{3}} \\ &= \frac{\sqrt{507-144}}{13\sqrt{3}} \\ &= \frac{\sqrt{363}}{13\sqrt{3}} \\ &= \frac{11\sqrt{3}}{13\sqrt{3}} \\ \sin \angle TAD &= \frac{11}{13} \end{align}$
Luas segitiga TAD:
$\begin{align}\frac{1}{2}.AD.TO &= \frac{1}{2}.AD.AT.\sin \angle TAD \\ TO &= AT.\sin \angle TAD \\ TO &= 13.\frac{11}{13} \\ TO &= 11 \end{align}$
Jadi, jarak titik T ke AD adalah 11 cm.
Jawaban: C
(A) $\frac{12}{41}\sqrt{41}$
(B) $\frac{24}{41}\sqrt{41}$
(C) $\frac{30}{41}\sqrt{41}$
(D) $\frac{36}{41}\sqrt{41}$
(E) $2\sqrt{41}$

Jarak titik D dan TH adalah panjang ruas garis PD.
Segitiga BAD siku-siku di titik A maka:
$\begin{align}BD &= \sqrt{BA^2+AD^2} \\ &= \sqrt{6^2+6^2} \\ &= \sqrt{72} \\ BD &= 6\sqrt{2} \end{align}$
$\begin{align}TD &= \frac{1}{2}BD \\ &= \frac{1}{2}.6\sqrt{2} \\ TD &= 3\sqrt{2} \end{align}$
Segitiga TDH siku-siku di titik D maka:
$\begin{align}TH &= \sqrt{TD^2+DH^2} \\ &= \sqrt{\left( 3\sqrt{2} \right)^2+8^2} \\ &= \sqrt{18+64} \\ TH &= \sqrt{82} \end{align}$
Luas segitiga TDH:
$\begin{align}\frac{1}{2}\times TH\times PD &= \frac{1}{2}\times TD\times DH \\ TH\times PD &= TD\times DH \\ \sqrt{82}\times PD &= 3\sqrt{2}\times 8 \\ PD &= \frac{24}{\sqrt{41}}\times \frac{\sqrt{41}}{\sqrt{41}} \\ PD &= \frac{24}{41}\sqrt{41} \end{align}$
Jadi, jarak titik D dan TH adalah $\frac{24}{41}\sqrt{41}$.
Jawaban: B
Tata Cara Belajar:
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cocokkanlah jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
SELAMAT BELAJAR
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cocokkanlah jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
SELAMAT BELAJAR
Soal No. 1
Diketahui kubus ABCD.EFGH, rusuk-rusuknya 10 cm. Jarak titik F ke garis AC adalah … cm.(A) $3\sqrt{5}$
(B) $5\sqrt{2}$
(C) $5\sqrt{6}$
(D) $10\sqrt{2}$
(E) $10\sqrt{6}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Dari gambar, jarak titik F ke garis AC adalah jarak titik F ke titik Q yaitu panjang ruas garis FQ.
Perhatikan segitiga ACF,
AC = CF = AF = $10\sqrt{2}$ (diagonal sisi kubus).
Karena AF = CF maka garis tinggi FQ membagi dua sama panjang garis AC, sehingga diperoleh:
$\begin{align}AQ &= \frac{1}{2}AC \\ &= \frac{1}{2}.10\sqrt{2} \\ AQ &= 5\sqrt{2} \end{align}$
Pada segitiga AQF siku-siku di Q maka:
$\begin{align}FQ &= \sqrt{AF^2-AQ^2} \\ &= \sqrt{(10\sqrt{2})^2-(5\sqrt{2})^2} \\ &= \sqrt{200-50} \\ &= \sqrt{150} \\ FQ &= 5\sqrt{6} \end{align}$
Jadi, jarak titik F ke garis AC adalah $5\sqrt{6}$ cm.
Jawaban: C
Soal No. 2
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik H ke garis DF adalah … cm.(A) $3\sqrt{5}$
(B) $2\sqrt{6}$
(C) $\sqrt{6}$
(D) $2\sqrt{3}$
(E) $\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik H ke garis DF adalah panjang ruas garis HP.
HF adalah diagonal sisi kubus, maka:
$HF=s\sqrt{2}=6\sqrt{2}$
DF adalah diagonal ruang kubus, maka:
$DF=s\sqrt{3}=6\sqrt{3}$
Perhatikan segitiga DHF, dengan menggunakan rumus luas segitiga maka:
$\begin{align}\frac{1}{2}.DF.HP &= \frac{1}{2}.HD.HF \\ HP &= \frac{HD.HF}{DF} \\ &= \frac{6\times 6\sqrt{2}}{6\sqrt{3}} \\ &= \frac{6\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ HP &= 2\sqrt{6} \end{align}$
Cara alternatif:
Jarak titik sudut kubus (titik H) ke diagonal ruang kubus (garis DF) adalah $\frac{s}{3}\sqrt{6} = \frac{6}{3}\sqrt{6} = 2\sqrt{6}$.
Jawaban: B
Soal No. 3
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Titik M adalah titik tengah rusuk BC. Jarak titik M ke garis EG adalah … cm.(A) 6
(B) $6\sqrt{2}$
(C) $6\sqrt{3}$
(D) $6\sqrt{6}$
(E) 12
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik M ke garis EG adalah panjang ruas garis MP.
Perhatikan segitiga EBM.
BE adalah diagonal sisi kubus, maka:
$BE=s\sqrt{2}=8\sqrt{2}$
$\begin{align}EM &= \sqrt{BE^2+BM^2} \\ &= \sqrt{(8\sqrt{2})^2+4^2} \\ &= \sqrt{128+16} \\ &= \sqrt{144} \\ EM &= 12 \end{align}$
Perhatikan segitiga MCG.
$\begin{align}GM &= \sqrt{CM^2+CG^2} \\ &= \sqrt{4^2+8^2} \\ &= \sqrt{16+64} \\ &= \sqrt{80} \\ GM &= 4\sqrt{5} \end{align}$
Perhatikan segitiga MEG, dengan menggunakan aturan cosinus maka:
$\begin{align}\cos \angle MEG &= \frac{EG^2+EM^2-GM^2}{2.EG.EM} \\ &= \frac{(8\sqrt{2}^2+12^2-(4\sqrt{5})^2}{2.8\sqrt{2}.12} \\ &= \frac{128+144-80}{192\sqrt{2}} \\ &= \frac{192}{192\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ \cos \angle MEG &= \frac{1}{2}\sqrt{2} \\ \angle MEG &= 45^\circ \end{align}$
Perhatikan segitiga MEG, dengan menggunakan rumus luas segitiga maka:
$\begin{align}\frac{1}{2}.EG.MP &= \frac{1}{2}.EG.EM.\sin \angle MEG \\ MP &= EM.\sin 45^\circ \\ MP &= 12.\frac{1}{2}\sqrt{2} \\ MP &= 6\sqrt{2} \end{align}$
Jawaban: B
Soal No. 4
Diketahui kubus ABCD.EFGH dengan panjang rusuk $\sqrt{3}$ cm dan titik T pada garis AD dengan panjang AT = 1 cm. Jarak titik A ke garis BT adalah … cm.(A) $\frac{1}{2}$
(B) $\frac{1}{3}\sqrt{3}$
(C) $\frac{1}{2}\sqrt{3}$
(D) 1
(E) $\frac{2}{3}\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Perhatikan segitiga TAB, siku-siku di A maka:
$\begin{align}BT &= \sqrt{AB^2+AT^2} \\ &= \sqrt{(\sqrt{3})^2+1^2} \\ BT &= 2 \end{align}$
Jarak titik A ke garis BT adalah panjang AP.
$\begin{align}AP &= \frac{AB\times AT}{BT} \\ &= \frac{\sqrt{3}\times 1}{2} \\ AP &= \frac{1}{2}\sqrt{3} \end{align}$
Jawaban: C
Soal No. 5
Pada kubus ABCD.EFGH dengan panjang rusuk 4 cm, titik P terletak di tengah-tengah EH. Jarak titik P ke garis BG adalah ... cm.(A) $2\sqrt{2}$
(B) $2\sqrt{3}$
(C) $3\sqrt{2}$
(D) $3\sqrt{3}$
(E) $2\sqrt{5}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik P ke garis BG adalah panjang ruas garis PQ.
Perhatikan segitiga BEP, siku-siku di titik E.
BE adalah diagonal sisi kubus, maka:
$BE=s\sqrt{2}=4\sqrt{2}$
$\begin{align}BP &= \sqrt{BE^2+EP^2} \\ &= \sqrt{(4\sqrt{2})^2+2^2} \\ &= \sqrt{32+4} \\ &= \sqrt{36} \\ BP &= 6 \end{align}$
Perhatikan segitiga PHG, siku-siku di titik H.
$\begin{align}PG &= \sqrt{HP^2+HG^2} \\ &= \sqrt{2^2+4^2} \\ &= \sqrt{20} \\ PG &= 2\sqrt{5} \end{align}$
BG adalah diagonal sisi kubus, maka:
$BG=s\sqrt{2}=4\sqrt{2}$
Perhatikan segitiga BGP:
Arutan cosinus:
$\begin{align}\cos \angle BGP &= \frac{BG^2+GP^2-BP^2}{2.BG.GP} \\ &= \frac{(4\sqrt{2})^2+(2\sqrt{5})^2-6^2}{2.4\sqrt{2}.2\sqrt{5}} \\ &= \frac{32+20-36}{16\sqrt{10}} \\ &= \frac{16}{16\sqrt{10}} \\ \cos \angle BGP &= \frac{1}{\sqrt{10}} \end{align}$
$\sin \angle BGP = \frac{\sqrt{(\sqrt{10})^2-1^2}}{\sqrt{10}} = \frac{3}{\sqrt{10}}$
Dengan menggunakan luas segitiga BPG maka:
$\begin{align}\frac{1}{2}.BG.PQ &= \frac{1}{2}.GB.GP.\sin \angle BGP \\ PQ &= GP.\sin \angle BGP \\ &= 2\sqrt{5}.\frac{3}{\sqrt{10}} \\ &= \frac{6}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ PQ &= 3\sqrt{2} \end{align}$
Jawaban: C
Soal No. 6
Diketahui kubus ABCD.EFGH dengan panjang rusuknya 6 cm. Jika titik P berada pada perpanjangan garis HG sehingga HG = GP, maka jarak titik G ke garis AP adalah ... cm.(A) $\sqrt{6}$
(B) $2\sqrt{3}$
(C) $2\sqrt{6}$
(D) $4\sqrt{3}$
(E) $4\sqrt{6}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik G ke garis AP adalah panjang ruas garis GQ.
AH adalah diagonal sisi kubus, maka:
$AH=s\sqrt{2}=6\sqrt{2}$
$\begin{align}AP &= \sqrt{AH^2+HP^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+12^2} \\ &= \sqrt{72+144} \\ &= \sqrt{216} \\ AP &= 6\sqrt{6} \end{align}$
Segitiga AHP sebangun dengan segitiga GQP, maka perbandingan sisi-sisi yang bersesuaian adalah:
$\begin{align}\frac{GQ}{AH} &= \frac{GP}{AP} \\ \frac{GQ}{6\sqrt{2}} &= \frac{6}{6\sqrt{3}} \\ GQ &= \frac{6\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ GQ &= 2\sqrt{6} \end{align}$
Jawaban: C
Soal No. 7
Panjang rusuk kubus ABCD.EFGH adalah 5 cm. Jarak titik G ke diagonal HB adalah ... cm.(A) $\frac{5}{3}\sqrt{6}$
(B) $\frac{4}{3}\sqrt{6}$
(C) $\sqrt{6}$
(D) $\frac{2}{3}\sqrt{6}$
(E) $\frac{1}{3}\sqrt{6}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik G ke garis HB adalah panjang ruas garis GP.
Perhatikan segitiga BCG siku-siku di titik C, maka:
$\begin{align}BG &= \sqrt{BC^2+CG^2} \\ &= \sqrt{5^2+5^2} \\ &= \sqrt{50} \\ BG &= 5\sqrt{2} \end{align}$
Perhatikan segitiga BGH siku-siku di titik G, maka:
$\begin{align}HB &= \sqrt{BG^2+GH^2} \\ &= \sqrt{\left( 5\sqrt{2} \right)^2+5^2} \\ &= \sqrt{50+25} \\ &= \sqrt{75} \\ HB &= 5\sqrt{3} \end{align}$
Luas segitiga BGH:
$\begin{align}\frac{1}{2}.HB.GP &= \frac{1}{2}.HG.BG \\ HB.GP &= HG.BG \\ 5\sqrt{3}.GP &= 5.5\sqrt{2} \\ GP &= \frac{5\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ GP &= \frac{5}{3}\sqrt{6} \end{align}$
Jadi, jarak titik G ke garis HB adalah $\frac{5}{3}\sqrt{6}$ cm.
Jawaban: A
Soal No. 8
Kubus ABCD.EFGH dengan AB = 6, jarak titik B ke diagonal AG adalah ...(A) $5\sqrt{6}$
(B) $4\sqrt{6}$
(C) $3\sqrt{6}$
(D) $2\sqrt{6}$
(E) $\sqrt{2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik B ke garis AG adalah panjang ruas garis BP.
Perhatikan segitiga BCG siku-siku di titik C, maka:
$\begin{align}BG^2 &= BC^2+CG^2 \\ &= 6^2+6^2 \\ BG^2=72 \end{align}$
Perhatikan segitiga ABG siku-siku di titik B, maka:
$\begin{align}AG &= \sqrt{AB^2+BG^2} \\ &= \sqrt{6^2+\left( 6\sqrt{2} \right)^2} \\ &= \sqrt{36+72} \\ &= \sqrt{108} \\ AG &= 6\sqrt{3} \end{align}$
Luas segitiga ABG:
$\begin{align}\frac{1}{2}.AG.BP &= \frac{1}{2}.AB.BG \\ AG.BP &= AB.BG \\ 6\sqrt{3}.BP &= 6.6\sqrt{2} \\ BP &= \frac{6\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ BP &= 2\sqrt{6} \end{align}$
Jawaban: D
Soal No. 9
Limas beraturan T.ABCD dengan panjang rusuk alas 12 cm dan panjang rusuk tegak $12\sqrt{2}$ cm. Jarak titik A ke garis TC adalah ... cm(A) $6\sqrt{6}$
(B) $2\sqrt{10}$
(C) $2\sqrt{11}$
(D) $4\sqrt{3}$
(E) $2\sqrt{13}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik A ke garis TC adalah panjang ruas garis AK.
perhatikan segitiga ABC siku-siku di titik C maka:
$\begin{align}AC &= \sqrt{AB^2+BC^2} \\ &= \sqrt{12^2+12^2} \\ &= \sqrt{{{2.12}^{2}}} \\ AC &= 12\sqrt{2} \end{align}$
Perhatikan segitiga TAC:
AT = $12\sqrt{2}$, $AC=12\sqrt{3}$
Karena AT = AC dan AK adalah garis tinggi terhadap TC, maka AK membagi dua sama panjang garis TC sehingga kita peroleh:
$\begin{align}CK &= \frac{1}{2}TC \\ &= \frac{1}{2}.12\sqrt{2} \\ CK &= 6\sqrt{2} \end{align}$
Perhatikan segitiga AKC siku-siku di titik K maka berlaku pythagoras:
$\begin{align}AK &= \sqrt{AC^2-CK^2} \\ &= \sqrt{\left( 12\sqrt{2} \right)^2-\left( 6\sqrt{2} \right)^2} \\ &= \sqrt{288-72} \\ &= \sqrt{216} \\ AK &= 6\sqrt{6} \end{align}$
Jadi, jarak titik A ke garis TC adalah $6\sqrt{6}$ cm.
Jawaban: A
Soal No. 10
Kubus ABCD.EFGH dengan AB = 6 cm, titik P berada di tengah-tengah FG, maka jarak titik A ke garis DP adalah ... cm.(A) 6
(B) $6\sqrt{2}$
(C) $6\sqrt{3}$
(D) $6\sqrt{6}$
(E) $4\sqrt{2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik A ke garis DP adalah panjang ruas garis AQ.
AF adalah diagonal sisi kubus maka:
$AF=s\sqrt{2}=6\sqrt{2}$
Perhatikan segitiga PRD siku-siku di titik R maka:
$PR=AF=6\sqrt{2}$
$\begin{align}PD &= \sqrt{PR^2+RD^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+3^2} \\ &= \sqrt{72+9} \\ &= \sqrt{81} \\ PD &= 9 \end{align}$
Perhatikan segitiga APD, maka luas segitiga APD:
$\begin{align}\frac{1}{2}.PD.AQ &= \frac{1}{2}.AD.PR \\ PD.AQ &= AD.PR \\ 9.AD &= 6.9 \\ AD &= 6 \end{align}$
Jawaban: A
Soal No. 11
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jika T titik tengah HG, R titik tengah CG, maka jarak R ke BT adalah ... cm(A) $\sqrt{10}$
(B) $3\sqrt{5}$
(C) $\frac{9}{5}$
(D) $3\sqrt{2}$
(E) 3
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik R ke garis BT adalah panjang ruas garis PR.
Segitiga BCR siku-siku di titik C, maka:
$\begin{align}BR &= \sqrt{BC^2+CR^2} \\ &= \sqrt{6^2+3^2} \\ &= \sqrt{36+9} \\ &= \sqrt{45} \\ BR &= 3\sqrt{5} \end{align}$
Segitiga RGT siku-siku di titik G, maka:
$\begin{align}RT &= \sqrt{RG^2+GT^2} \\ &= \sqrt{3^2+3^2} \\ &= \sqrt{18} \\ RT &= 3\sqrt{2} \end{align}$
BG diagonal sisi kubus, maka $BG=6\sqrt{2}$.
Segitiga BGT siku-siku di titik G, maka:
$\begin{align}BT &= \sqrt{BG^2+GT^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+3^2} \\ &= \sqrt{72+9} \\ &= \sqrt{81} \\ BT &= 9 \end{align}$
Pada segitiga BRT, berlaku aturan cosinus sebagai berikut:
$\begin{align}\cos \angle RBT &= \frac{BR^2+BT^2-RT^2}{2.BR.BT} \\ &= \frac{\left( 3\sqrt{5} \right)^2+9^2-\left( 3\sqrt{2} \right)^2}{2.3\sqrt{5}.9} \\ &= \frac{45+81-18}{54\sqrt{5}} \\ &= \frac{108}{54\sqrt{5}} \\ \cos \angle RBT &= \frac{2}{\sqrt{5}} \end{align}$
Dengan perbandingan trigonometri diperoleh:
$\sin \angle RBT = \frac{\sqrt{(\sqrt{5})^2-2^2}}{\sqrt{5}} = \frac{1}{\sqrt{5}}$
Luas segitiga RBT:
$\begin{align}\frac{1}{2}.BT.PR &= \frac{1}{2}.BT.BR.\sin \angle RBT \\ PR &= BR.\sin \angle RBT \\ PR &= 3\sqrt{5}.\frac{1}{\sqrt{5}} \\ PR &= 3 \end{align}$
Jadi, jarak titik R ke BT adalah 3 cm.
Jawaban: E
Soal No. 12
SIMAK UI 2009 Kode 934. Diketahui kubus ABCD.EFGH dengan panjang sisi 5 cm. Jarak titik B ke diagonal EG adalah ... cm.(A) $\frac{5}{2}\sqrt{3}$
(B) $\frac{5}{2}\sqrt{6}$
(C) $5\sqrt{3}$
(D) $128\sqrt{3}$
(E) $3\sqrt{2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik B ke diagonal EG adalah panjang ruas garis BP.
BE, BG, dan EG adalah diagonal sisi kubus maka:
BE = BG = EG = $s\sqrt{2}=5\sqrt{2}$
Karena BE = BG dan BP adalah garis tinggi terhadap sisi EG maka BP membagi dua sama panjang garis EG sehingga diperoleh:
$\begin{align}EP &= \frac{1}{2}EG \\ &= \frac{1}{2}.5\sqrt{2} \\ EP &= \frac{5\sqrt{2}}{2} \end{align}$
Perhatikan segitiga BPE siku-siku di titik P maka:
$\begin{align}BP &= \sqrt{BE^2-EP^2} \\ &= \sqrt{\left( 5\sqrt{2} \right)^2-\left( \frac{5\sqrt{2}}{2} \right)^2} \\ &= \sqrt{50-\frac{50}{4}} \\ &= \sqrt{\frac{150}{4}} \\ &= \sqrt{\frac{25\times 6}{4}} \\ BP &= \frac{5}{2}\sqrt{6} \end{align}$
Jadi, jarak titik B ke diagonal EG adalah $\frac{5}{2}\sqrt{6}$ cm.
Jawaban: B
Soal No. 13
SIMAK UI 2010 Kode 508. Diberikan prisma tegak segitiga siku-siku ABC.DEF dengan alas $\Delta ABC$ siku-siku di B. Panjang rusuk tegak prisma $2\sqrt{2}$ satuan, panjang AB = panjang BC = 4 satuan, maka jarak A ke EF adalah ... satuan.(A) 4
(B) $4\sqrt{2}$
(C) $4\sqrt{3}$
(D) $2\sqrt{6}$
(E) $4\sqrt{6}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Bidang ABED tegak lurus dengan bidang BCFE.
AE terletak pada bidang ABED dan EF terletak pada bidang BCFE maka $AE\bot EF$.
Perhatikan segitiga AEF siku-siku di titik E, maka jarak titik A ke garis EF adalah panjang ruas garis AE.
Untuk menghitung panjang AE perhatikan segitiga ABD siku-siku di titik B, maka:
$\begin{align}AE &= \sqrt{AB^2+BE^2} \\ &= \sqrt{4^2+\left( 2\sqrt{2} \right)^2} \\ &= \sqrt{16+8} \\ &= \sqrt{24} \\ AE &= 2\sqrt{6} \end{align}$
Jadi, jarak titik A ke EF adalah $2\sqrt{6}$ cm.
Jawaban: D
Soal No. 14
Diberikan bidang empat beraturan T.ABC dengan panjang rusuk 12 cm. Jika titik P adalah titik tengah rusuk BC, maka jarak titik P ke garis AT adalah ... cm.(A) $3\sqrt{2}$
(B) $4\sqrt{2}$
(C) $6\sqrt{2}$
(D) $6\sqrt{3}$
(E) $4\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik P ke garis AT adalah panjang ruas garis PQ.
Perhatikan segitiga TBC, karena TA = TB dan titik P membagi dua sama panjang sisi BC, maka $TP\bot BC$.
Perhatikan segitiga TPC siku-siku di titik P maka:
$\begin{align}TP &= \sqrt{TC^2-PC^2} \\ &= \sqrt{12^2-6^2} \\ &= \sqrt{144-36} \\ &= \sqrt{108} \\ TP &= 6\sqrt{3} \end{align}$
Perhatikan segitiga ABC, karena AB = AC dan titik P membagi dua sama panjang sisi BC, maka $AP\bot BC$
Perhatikan segitiga BPA siku-siku di titik P maka:
$\begin{align}AP &= \sqrt{AB^2-BP^2} \\ &= \sqrt{12^2-6^2} \\ &= \sqrt{144-36} \\ &= \sqrt{108} \\ AP &= 6\sqrt{3} \end{align}$
Perhatikan segitiga TPA, karena AP = TP dan $PQ\bot AT$ maka TQ membagi dua sama panjang garis AT sehingga kita peroleh:
$AQ=\frac{1}{2}AT=\frac{1}{2}\times 12=6$
Segitiga AQP siku-siku di titik Q maka:
$\begin{align}PQ &= \sqrt{AP^2-AQ^2} \\ &= \sqrt{\left( 6\sqrt{3} \right)^2-6^2} \\ &= \sqrt{108-36} \\ &= \sqrt{72} \\ PQ &= 6\sqrt{2} \end{align}$
Jadi, jarak titik P ke garis AT adalah $6\sqrt{2}$ cm.
Jawaban: C
Soal No. 15
Diketahui balok ABCD.EFGH dengan AB = AD = 6 cm dan AE = $6\sqrt{2}$ cm. Jika K titik tengah EG maka jarak titik H ke garis DK adalah ... cm.(A) $\sqrt{5}$
(B) $\frac{3}{5}\sqrt{5}$
(C) $\frac{6}{5}\sqrt{5}$
(D) $\frac{3}{5}\sqrt{10}$
(E) $\frac{6}{5}\sqrt{10}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik H ke garis DK adalah panjang ruas garis HL.
Pada segitiga HEF siku-siku di titik E maka:
$\begin{align}HF &= \sqrt{HE^2+EF^2} \\ &= \sqrt{6^2+6^2} \\ &= \sqrt{72} \\ HF &= 6\sqrt{2} \end{align}$
Titik K di tengah EG maka K juga ditengah HF.
$HK=\frac{1}{2}HF=\frac{1}{2}.6\sqrt{2}=3\sqrt{2}$
Segitiga DHK siku-siku di titik H, maka:
$\begin{align}DK &= \sqrt{HK^2+DH^2} \\ &= \sqrt{\left( 3\sqrt{2} \right)^2+\left( 6\sqrt{2} \right)^2} \\ &= \sqrt{18+72} \\ &= \sqrt{90} \\ DK &= 3\sqrt{10} \end{align}$
Luas segitiga DHK:
$\begin{align}\frac{1}{2}.DK.HL &= \frac{1}{2}.DH.HK \\ DK.HL &= DH.HK \\ 3\sqrt{10}.HL &= 6\sqrt{2}.3\sqrt{2} \\ HL &= \frac{12}{\sqrt{10}}\times \frac{\sqrt{10}}{\sqrt{10}} \\ HL &= \frac{12}{10}\sqrt{10} \\ HL &= \frac{6}{5}\sqrt{10} \end{align}$
Jadi, jarak titik H ke garis DK adalah $\frac{6}{5}\sqrt{10}$ cm.
Jawaban: E
Soal No. 16
Diketahui kubus ABCD.EFGH yang panjang rusuknya 6 cm. Titik P, Q, dan R berturut-turut merupakan titik tengah rusuk EH, BF, dan CG. Jarak titik P ke garis QR adalah ... cm.(A) $3\sqrt{7}$
(B) $3\sqrt{6}$
(C) $3\sqrt{5}$
(D) $3\sqrt{3}$
(E) $2\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik P ke garis QR adalah panjang ruas garis PS.
Karena PQ = PR dan $PS\bot QR$ maka PS membagi dua sama panjang garis QR.
Perhatikan, PS dan EQ terletak pada satu bidang.
EQ sejajar dengan PS, dan PS = EQ.
Perhatikan segitiga EFQ siku-siku di titik F maka:
$\begin{align}EQ &= \sqrt{EF^2+FQ^2} \\ &= \sqrt{6^2+3^2} \\ &= \sqrt{36+9} \\ &= \sqrt{45} \\ EQ &= 3\sqrt{5} \end{align}$
PS = EQ = $3\sqrt{5}$
Jadi, jarak titik P ke garis QR adalah $3\sqrt{5}$ cm.
Jawaban: C
Soal No. 17
Diketahui limas beraturan T.ABCD dengan rusuk alas $a\sqrt{2}$ cm dan rusuk tegaknya $2a$ cm. Jika O adalah perpotongan diagonal AC dan BD, maka jarak O ke garis TC adalah ... cm.(A) $\frac{1}{2}a\sqrt{3}$
(B) $\frac{1}{2}a\sqrt{2}$
(C) $\frac{1}{3}a\sqrt{3}$
(D) $\frac{1}{3}a\sqrt{2}$
(E) $\frac{1}{2}a\sqrt{6}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
$\begin{align}AC &= \sqrt{AB^2+BC^2} \\ &= \sqrt{\left( a\sqrt{2} \right)^2+\left( a\sqrt{2} \right)^2} \\ &= \sqrt{4a^2} \\ AC &= 2a \end{align}$
$OC=\frac{1}{2}AC=\frac{1}{2}.2a=a$
Perhatikan segitiga TOC siku-siku di titik O maka:
$\begin{align}OT &= \sqrt{TC^2-OC^2} \\ &= \sqrt{(2a)^2-a^2} \\ &= \sqrt{3a^2} \\ OT &= a\sqrt{3} \end{align}$
Luas segitiga TOC:
$\begin{align}\frac{1}{2}\times TC\times OP &= \frac{1}{2}\times OT\times OC \\ TC\times OP &= OT\times OC \\ 2a\times OP &= a\sqrt{3}\times a \\ OP &= \frac{1}{2}a\sqrt{3} \end{align}$
Jadi, jarak titik O ke garis TC adalah $\frac{1}{2}a\sqrt{3}$ cm.
Jawaban: A
Soal No. 18
Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. M adalah titik tengah EH. Jarak titik M ke AG adalah ... cm.(A) $4\sqrt{6}$
(B) $4\sqrt{5}$
(C) $4\sqrt{3}$
(D) $4\sqrt{2}$
(E) 4
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik M ke AG adalah panjang ruas garis MN.
Perhatikan segitiga AEM siku-siku di titik E maka:
$\begin{align}AM &= \sqrt{AE^2+EM^2} \\ &= \sqrt{8^2+4^2} \\ &= \sqrt{64+16} \\ &= \sqrt{80} \\ AM &= 4\sqrt{5} \end{align}$
MG = $AM=4\sqrt{5}$
AG adalah diagonal ruang kubus, maka $AG=s\sqrt{3}=8\sqrt{3}$.
Segitiga AMG segitiga sama kaki (AM=MG), maka MN adalah garis tinggi yang membagi dua AG di titik N, maka:
$\begin{align}AN &= \frac{1}{2}.AG \\ &= \frac{1}{2}.8\sqrt{3} \\ AN &= 4\sqrt{3} \end{align}$
Segitiga ANM siku-siku di titik N maka:
$\begin{align}MN &= \sqrt{AM^2-AN^2} \\ &= \sqrt{\left( 4\sqrt{5} \right)^2-\left( 4\sqrt{3} \right)^2} \\ &= \sqrt{80-48} \\ &= \sqrt{32} \\ MN &= 4\sqrt{2} \end{align}$
Jadi, jarak titik M ke AG adalah $4\sqrt{2}$ cm.
Jawaban: D
Soal No. 19
Limas T.ABC pada gambar di bawah.
Merupakan limas segitiga beraturan, jarak titik T ke AD adalah ...
(A) $4\sqrt{3}$
(B) $6\sqrt{3}$
(C) 11
(D) $\sqrt{133}$
(E) 12
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik T ke AD adalah panjang ruas garis TO.
Segitiga BDA siku-siku di titik D maka:
$\begin{align}AD &= \sqrt{AB^2-BD^2} \\ &= \sqrt{12^2-6^2} \\ &= \sqrt{144-36} \\ &= \sqrt{108} \\ AD &= 6\sqrt{3} \end{align}$
Segitiga TDC siku-siku di titik D maka:
$\begin{align}TD &= \sqrt{TC^2-DC^2} \\ &= \sqrt{13^2-6^2} \\ &= \sqrt{169-36} \\ TD &= \sqrt{133} \end{align}$
Dengan aturan cosinus pada segitiga TAD maka:
$\begin{align}\cos \angle TAD &= \frac{TA^2+AD^2-TD^2}{2.TA.AD} \\ &= \frac{13^2+\left( 6\sqrt{3} \right)^2-\left( \sqrt{133} \right)^2}{2.13.6\sqrt{3}} \\ &= \frac{169+108-133}{156\sqrt{3}} \\ &= \frac{144}{156\sqrt{3}} \\ \cos \angle TAD &= \frac{12}{13\sqrt{3}} \end{align}$
Dengan perbandingan trigonometri:
$\begin{align}\sin \angle TAD &= \frac{\sqrt{\left( 13\sqrt{3} \right)^2-12^2}}{13\sqrt{3}} \\ &= \frac{\sqrt{507-144}}{13\sqrt{3}} \\ &= \frac{\sqrt{363}}{13\sqrt{3}} \\ &= \frac{11\sqrt{3}}{13\sqrt{3}} \\ \sin \angle TAD &= \frac{11}{13} \end{align}$
Luas segitiga TAD:
$\begin{align}\frac{1}{2}.AD.TO &= \frac{1}{2}.AD.AT.\sin \angle TAD \\ TO &= AT.\sin \angle TAD \\ TO &= 13.\frac{11}{13} \\ TO &= 11 \end{align}$
Jadi, jarak titik T ke AD adalah 11 cm.
Jawaban: C
Soal No. 20
Prisma segi-4 beraturan ABCD.EFGH dengan rusuk 6 cm dan tinggi prisma 8 cm. Titik potong diagonal AC dan BD adalah T. Jarak titik D dan TH = ... cm.(A) $\frac{12}{41}\sqrt{41}$
(B) $\frac{24}{41}\sqrt{41}$
(C) $\frac{30}{41}\sqrt{41}$
(D) $\frac{36}{41}\sqrt{41}$
(E) $2\sqrt{41}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik D dan TH adalah panjang ruas garis PD.
Segitiga BAD siku-siku di titik A maka:
$\begin{align}BD &= \sqrt{BA^2+AD^2} \\ &= \sqrt{6^2+6^2} \\ &= \sqrt{72} \\ BD &= 6\sqrt{2} \end{align}$
$\begin{align}TD &= \frac{1}{2}BD \\ &= \frac{1}{2}.6\sqrt{2} \\ TD &= 3\sqrt{2} \end{align}$
Segitiga TDH siku-siku di titik D maka:
$\begin{align}TH &= \sqrt{TD^2+DH^2} \\ &= \sqrt{\left( 3\sqrt{2} \right)^2+8^2} \\ &= \sqrt{18+64} \\ TH &= \sqrt{82} \end{align}$
Luas segitiga TDH:
$\begin{align}\frac{1}{2}\times TH\times PD &= \frac{1}{2}\times TD\times DH \\ TH\times PD &= TD\times DH \\ \sqrt{82}\times PD &= 3\sqrt{2}\times 8 \\ PD &= \frac{24}{\sqrt{41}}\times \frac{\sqrt{41}}{\sqrt{41}} \\ PD &= \frac{24}{41}\sqrt{41} \end{align}$
Jadi, jarak titik D dan TH adalah $\frac{24}{41}\sqrt{41}$.
Jawaban: B

Post a Comment for "Soal Jarak Titik ke Garis pada Dimensi Tiga dan Pembahasan"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.