Soal Jarak Titik ke Titik pada Dimensi Tiga dan Pembahasan
Berikut ini adalah Kumpulan Soal Jarak Titik ke Titik pada Dimensi Tiga dan Pembahasannya. Bagi adik-adik silahkan dipelajari dan jangan lupa share/bagikan ke media sosial kalian, agar manfaat postingan ini dapat dirasakan oleh siswa/i yang lain. Terima kasih.
(A) 26 cm
(B) 25 cm
(C) 24 cm
(D) 23 cm
(E) 22 cm

Jarak titik H ke titik B adalah panjang ruas garis HB.
Perhatikan segitiga BAD siku-siku di titik C, maka dengan pythagoras diperoleh:
$\begin{align}BD &= \sqrt{AB^2+AD^2} \\ &= \sqrt{8^2+6^2} \\ &= \sqrt{64+36} \\ &= \sqrt{100} \\ BD &= 10 \end{align}$
Perhatikan segitiga BDH siku-siku di titik D, maka dengan pythagoras diperoleh:
$\begin{align}HB &= \sqrt{BD^2+DH^2} \\ &= \sqrt{10^2+24^2} \\ &= \sqrt{100+576} \\ &= \sqrt{676} \\ HB &= 26 \end{align}$
Jadi, jarak titik H ke titik B adalah 26 cm.
Cara alternatif:
HB adalah diagonal ruang balok, maka:
$\begin{align}HB &= \sqrt{p^2+l^2+t^2} \\ &= \sqrt{8^2+6^2+4^2} \\ &= \sqrt{64+36+576} \\ &= \sqrt{676} \\ HB &= 26 \end{align}$
Jawaban: A
(A) $\sqrt{17}$
(B) $2\sqrt{17}$
(C) $3\sqrt{17}$
(D) 4
(E) 8

Perhatikan segitiga AEP siku-siku di titik E, maka:
$\begin{align}AP &= \sqrt{AE^2+EP^2} \\ &= \sqrt{8^2+4^2} \\ &= \sqrt{64+16} \\ &= \sqrt{80} \\ AP &= 4\sqrt{5} \end{align}$
Perhatikan segitiga CHP siku-siku di titik H, maka:
$\begin{align}CP &= \sqrt{CH^2+PH^2} \\ &= \sqrt{(8\sqrt{2})^2+4^2} \\ &= \sqrt{128+16} \\ &= \sqrt{144} \\ CP &= 12 \end{align}$
Titik Q ditengah-tengah CP, maka QP = QC = $\frac{1}{2}CP$ = 6 cm.
AC = diagonal sisi kubus, maka:
$AC=s\sqrt{2}=8\sqrt{2}$
Perhatikan segitiga CAP, dengan dalil steward maka:
$\begin{align}AQ^2.PC &= PQ.AC^2+CQ.AP^2-PQ.CQ.PC \\ AQ^2.12 &= 6.\left( 8\sqrt{2} \right)^2+6.\left( 4\sqrt{5} \right)^2-6.6.12 \\ 12.AQ^2 &= 6\times 128+6\times 80-144 \\ 4AQ^2 &= 2\times 128+2\times 80-72 \\ AQ^2 &= 2\times 32+2\times 20-18 \\ AQ^2 &= 86 \\ AQ &= \sqrt{86} \\ AQ &= 2\sqrt{17} \end{align}$
Jawaban: B
(A) $9\sqrt{6}$
(B) $\frac{18\sqrt{3}}{5}$
(C) $\frac{18\sqrt{6}}{5}$
(D) $9\sqrt{7}$
(E) $18\sqrt{2}$

Segitiga KDC sebangun dengan segitiga KLG, maka perbandingan sisi-sisinya adalah:
$\begin{align}\frac{LG}{DC} &= \frac{KG}{KC} \\ \frac{LG}{6} &= \frac{4}{10} \\ LG &= \frac{24}{10} \\ LG &= \frac{12}{5} \end{align}$
Perhatikan segitiga BGL siku-siku di titik G, maka dengan pythagoras diperoleh:
$\begin{align}BL &= \sqrt{BG^2+GL^2} \\ &= \sqrt{(6\sqrt{2})^2+\left( \frac{12}{5} \right)^2} \\ &= \sqrt{72+\frac{144}{25}} \\ &= \sqrt{\frac{1944}{25}} \\ BL &= \frac{18}{5}\sqrt{6} \end{align}$
Jawaban: C
(A) $\sqrt{t^2-\frac{3}{4}s^2}$
(B) $\sqrt{t^2+\frac{3}{4}s^2}$
(C) $\sqrt{t^2+s^2}$
(D) $\sqrt{t^2-s^2}$
(E) $\sqrt{t^2+\frac{1}{4}s^2}$

$GF=\frac{1}{2}EF=\frac{1}{2}s$
DG adalah garis tinggi segitiga DEF, maka:
$\begin{align}DG &= \sqrt{DF^2-GF^2} \\ &= \sqrt{s^2-\left( \frac{1}{2}s \right)^2} \\ &= \sqrt{s^2-\frac{s^2}{4}} \\ &= \sqrt{\frac{3s^2}{4}} \\ DG &= \frac{1}{2}s\sqrt{3} \end{align}$
Perhatikan segitiga ADG siku-siku di titik D dengan pythagoras maka:
$\begin{align}AG &= \sqrt{AD^2+DG^2} \\ &= \sqrt{t^2+\left( \frac{1}{2}s\sqrt{3} \right)^2} \\ AG &= \sqrt{t^2+\frac{3s^2}{4}} \end{align}$
Jawaban: B
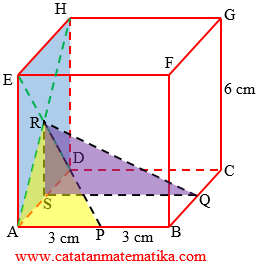
AH diagonal sisi kubus, maka:
$AH=s\sqrt{2}=6\sqrt{2}$
$AR=\frac{1}{2}AH=\frac{1}{2}.6\sqrt{2}=3\sqrt{2}$
Segitiga RAP siku-siku di titik A, maka:
$\begin{align}PR &= \sqrt{AP^2+AR^2} \\ &= \sqrt{3^2+ \left( 3\sqrt{2} \right)^2} \\ &= \sqrt{9+18} \\ &= \sqrt{27} \\ PR &= 3\sqrt{3} \end{align}$
Jadi, jarak titik P ke R adalah $3\sqrt{3}$ cm.
Perhatikan segitiga RSQ siku-siku di titik S, maka:
$\begin{align}QR &= \sqrt{RS^2+SQ^2} \\ &= \sqrt{3^2+6^2} \\ &= \sqrt{9+36} \\ &= \sqrt{45} \\ QR &= 3\sqrt{5} \end{align}$
Jadi, jarak titik Q ke titik R adalah $3\sqrt{5}$ cm.
(A) 10
(B) 12
(C) 13
(D) 14
(E) 15

Perhatikan segitiga DAB siku-siku di titik A, maka:
$\begin{align}BD^2 &= AB^2+AD^2 \\ &= 12^2+3^2 \\ BD^2 &= 153 \end{align}$
Perhatikan segitiga DBF siku-siku di titik B, maka:
$\begin{align}DF &= \sqrt{BD^2+BF^2} \\ &= \sqrt{153+4^2} \\ &= \sqrt{169} \\ DF &= 13 \end{align}$
Jadi, jarak titik D ke titik F adalah 13 cm.
Cara alternatif:
DF adalah diagonal ruang balok, maka:
$\begin{align}DF &= \sqrt{p^2+l^2+t^2} \\ &= \sqrt{12^2+3^2+4^2} \\ &= \sqrt{169} \\ DF &= 13 \end{align}$
Jawaban: C
(A) 10
(B) 12
(C) 13
(D) 14
(E) 15
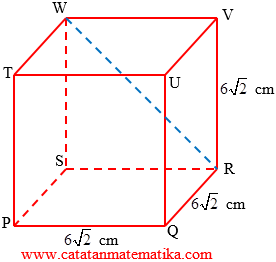
Perhatikan segitiga WSR siku-siku di titik S, maka:
$\begin{align}WR &= \sqrt{WS^2+SR^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+ \left( 6\sqrt{2} \right)^2} \\ &= \sqrt{72+72} \\ &= \sqrt{144} \\ WR &= 12 \end{align}$
Jadi, jarak titik W ke titik R adalah 12 cm.
Cara alternatif:
WR adalah diagonal sisi kubus, maka:
$WR=s\sqrt{2}=6\sqrt{2}.\sqrt{2}=12$
Jawaban: B
(A) $\frac{1}{2}$
(B) 1
(C) $\sqrt{2}$
(D) 2
(E) $\sqrt{3}$
AB = 2 cm, BC = 1 cm, AE =1 cm
Perhatikan gambar berikut!

Segitiga ADH siku-siku di titik D, maka:
$\begin{align}AH &= \sqrt{AD^2+DH^2} \\ &= \sqrt{1^2+1^2} \\ AH &= \sqrt{2} \end{align}$
Jawaban: C
(A) $3p\sqrt{2}$
(B) $\frac{3p}{\sqrt{2}}$
(C) $\frac{3}{2}p\sqrt{3}$
(D) $p^2\sqrt{19}$
(E) $p^2\sqrt{10}$
Perpanjang garis QP dan garis CB sehingga berpotongan di titik L.
Lukis dan perpanjang garis LR dan garis CD sehingga berpotongan di titik N.
Lukis garis NK, akhirnya diperoleh perluasan dari bidang PQR yaitu KLN dan bidang KLN memotong garis DH di titik S.
Hasilnya adalah seperti gambar berikut ini!

BD diagonal sisi kubus maka:
$BD=s\sqrt{2}=3p\sqrt{2}$.
Jarak titik S ke titik P adalah SP.
$SP=BD=3p\sqrt{2}$
Jawaban: A
(A) $2\sqrt{3}$
(B) $4\sqrt{3}$
(C) $2\sqrt{6}$
(D) $3\sqrt{6}$
(E) $4\sqrt{6}$
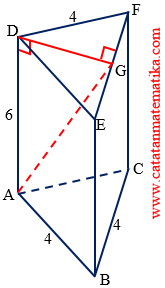
$GF=\frac{1}{2}EF=2$
DG adalah garis tinggi segitiga DEF, maka:
$\begin{align}DG &= \sqrt{DF^2-GF^2} \\ &= \sqrt{4^2-2^2} \\ &= \sqrt{16-4} \\ &= \sqrt{12} \\ DG &= 2\sqrt{3} \end{align}$
Perhatikan segitiga ADG siku-siku di titik D dengan pythagoras maka:
$\begin{align}AG &= \sqrt{AD^2+DG^2} \\ &= \sqrt{6^2+\left( 2\sqrt{3} \right)^2} \\ &= \sqrt{36+12} \\ &= \sqrt{48} \\ AG &= 4\sqrt{3} \end{align}$
Jawaban: B
(A) $4\sqrt{2}$
(B) $3\sqrt{6}$
(C) $3\sqrt{2}$
(D) 3
(E) $2\sqrt{3}$
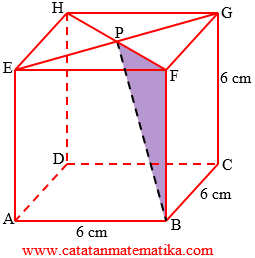
Jarak antara titik B dan titik P adalah BP.
FH adalah diagonal sisi kubus, maka:
$FH=s\sqrt{2}=6\sqrt{2}$
Titik P di tengah FH, maka:
$\begin{align}FP &= \frac{1}{2}.FH \\ &= \frac{1}{2}.6\sqrt{2} \\ FP &= 3\sqrt{2} \end{align}$
Segitiga BFP siku-siku di F, maka:
$\begin{align}BP &= \sqrt{BF^2+FP^2} \\ &= \sqrt{6^2+\left( 3\sqrt{2} \right)^2} \\ &= \sqrt{36+18} \\ &= \sqrt{54} \\ BP &= 3\sqrt{6} \end{align}$
Jadi, jarak antara titik B dan titik P adalah $3\sqrt{6}$ cm.
Jawaban: B
(A) $3\sqrt{6}$
(B) $8\sqrt{3}$
(C) $8\sqrt{2}$
(D) $12\sqrt{3}$
(E) $12\sqrt{2}$

Perhatikan segitiga DQC siku-siku di titik Q maka:
$\begin{align}DQ &= \sqrt{DC^2-QC^2} \\ &= \sqrt{16^2-8^2} \\ &= \sqrt{256-64} \\ &= \sqrt{192} \\ DQ &= 8\sqrt{3} \end{align}$
Perhatikan segitiga ABC, karena AB = AC dan titik Q membagi dua sama panjang sisi BC, maka $AQ\bot BC$
Perhatikan segitiga BQA siku-siku di titik Q maka:
$\begin{align}AQ &= \sqrt{AB^2-BQ^2} \\ &= \sqrt{16^2-8^2} \\ &= \sqrt{256-64} \\ &= \sqrt{192} \\ AQ &= 8\sqrt{3} \end{align}$
Perhatikan segitiga DAQ, karena AQ = DQ dan titik P di tengah AD maka $DQ\bot AD$.
Segitiga APQ siku-siku di titik P maka:
$\begin{align}PQ &= \sqrt{AQ^2-AP^2} \\ &= \sqrt{\left( 8\sqrt{3} \right)^2-8^2} \\ &= \sqrt{192-64} \\ &= \sqrt{128} \\ PQ &= 8\sqrt{2} \end{align}$
Jadi, panjang PQ adalah $8\sqrt{2}$ cm.
Jawaban: C
Tata Cara Belajar:
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cocokkanlah jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
SELAMAT BELAJAR
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cocokkanlah jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
SELAMAT BELAJAR
Soal No. 1
Diketahui balok ABCD.EFGH dengan AB = 8 cm, BC = 6 cm, dan BF = 24 cm. Jarak titik H ke titik B adalah ….(A) 26 cm
(B) 25 cm
(C) 24 cm
(D) 23 cm
(E) 22 cm
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak titik H ke titik B adalah panjang ruas garis HB.
Perhatikan segitiga BAD siku-siku di titik C, maka dengan pythagoras diperoleh:
$\begin{align}BD &= \sqrt{AB^2+AD^2} \\ &= \sqrt{8^2+6^2} \\ &= \sqrt{64+36} \\ &= \sqrt{100} \\ BD &= 10 \end{align}$
Perhatikan segitiga BDH siku-siku di titik D, maka dengan pythagoras diperoleh:
$\begin{align}HB &= \sqrt{BD^2+DH^2} \\ &= \sqrt{10^2+24^2} \\ &= \sqrt{100+576} \\ &= \sqrt{676} \\ HB &= 26 \end{align}$
Jadi, jarak titik H ke titik B adalah 26 cm.
Cara alternatif:
HB adalah diagonal ruang balok, maka:
$\begin{align}HB &= \sqrt{p^2+l^2+t^2} \\ &= \sqrt{8^2+6^2+4^2} \\ &= \sqrt{64+36+576} \\ &= \sqrt{676} \\ HB &= 26 \end{align}$
Jawaban: A
Soal No. 2
Pada kubus ABCD.EFGH dengan panjang rusuk 8 cm. Titik P pertengahan rusuk EH. Jika titik Q di tengah-tengah garis CP, maka jarak titik A ke Q adalah … cm.(A) $\sqrt{17}$
(B) $2\sqrt{17}$
(C) $3\sqrt{17}$
(D) 4
(E) 8
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Perhatikan segitiga AEP siku-siku di titik E, maka:
$\begin{align}AP &= \sqrt{AE^2+EP^2} \\ &= \sqrt{8^2+4^2} \\ &= \sqrt{64+16} \\ &= \sqrt{80} \\ AP &= 4\sqrt{5} \end{align}$
Perhatikan segitiga CHP siku-siku di titik H, maka:
$\begin{align}CP &= \sqrt{CH^2+PH^2} \\ &= \sqrt{(8\sqrt{2})^2+4^2} \\ &= \sqrt{128+16} \\ &= \sqrt{144} \\ CP &= 12 \end{align}$
Titik Q ditengah-tengah CP, maka QP = QC = $\frac{1}{2}CP$ = 6 cm.
AC = diagonal sisi kubus, maka:
$AC=s\sqrt{2}=8\sqrt{2}$
Perhatikan segitiga CAP, dengan dalil steward maka:
$\begin{align}AQ^2.PC &= PQ.AC^2+CQ.AP^2-PQ.CQ.PC \\ AQ^2.12 &= 6.\left( 8\sqrt{2} \right)^2+6.\left( 4\sqrt{5} \right)^2-6.6.12 \\ 12.AQ^2 &= 6\times 128+6\times 80-144 \\ 4AQ^2 &= 2\times 128+2\times 80-72 \\ AQ^2 &= 2\times 32+2\times 20-18 \\ AQ^2 &= 86 \\ AQ &= \sqrt{86} \\ AQ &= 2\sqrt{17} \end{align}$
Jawaban: B
Soal No. 3
Diketahui kubus ABCD.EFGH dengan titik K terletak pada perpanjangan CG sehingga GK = 4 cm. Garis DK memotong rusuk GH pada titik L. Jika panjang rusuk kubus adalah 6 cm, maka jarak titik L ke titik B adalah … cm.(A) $9\sqrt{6}$
(B) $\frac{18\sqrt{3}}{5}$
(C) $\frac{18\sqrt{6}}{5}$
(D) $9\sqrt{7}$
(E) $18\sqrt{2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Segitiga KDC sebangun dengan segitiga KLG, maka perbandingan sisi-sisinya adalah:
$\begin{align}\frac{LG}{DC} &= \frac{KG}{KC} \\ \frac{LG}{6} &= \frac{4}{10} \\ LG &= \frac{24}{10} \\ LG &= \frac{12}{5} \end{align}$
Perhatikan segitiga BGL siku-siku di titik G, maka dengan pythagoras diperoleh:
$\begin{align}BL &= \sqrt{BG^2+GL^2} \\ &= \sqrt{(6\sqrt{2})^2+\left( \frac{12}{5} \right)^2} \\ &= \sqrt{72+\frac{144}{25}} \\ &= \sqrt{\frac{1944}{25}} \\ BL &= \frac{18}{5}\sqrt{6} \end{align}$
Jawaban: C
Soal No. 4
Prisma tegak segitiga sama sisi ABC.DEF dengan panjang AB = s cm dan AD = t cm. Jika titik G terletak di tengah-tengah sisi EF, maka panjang AG = … cm.(A) $\sqrt{t^2-\frac{3}{4}s^2}$
(B) $\sqrt{t^2+\frac{3}{4}s^2}$
(C) $\sqrt{t^2+s^2}$
(D) $\sqrt{t^2-s^2}$
(E) $\sqrt{t^2+\frac{1}{4}s^2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar!
$GF=\frac{1}{2}EF=\frac{1}{2}s$
DG adalah garis tinggi segitiga DEF, maka:
$\begin{align}DG &= \sqrt{DF^2-GF^2} \\ &= \sqrt{s^2-\left( \frac{1}{2}s \right)^2} \\ &= \sqrt{s^2-\frac{s^2}{4}} \\ &= \sqrt{\frac{3s^2}{4}} \\ DG &= \frac{1}{2}s\sqrt{3} \end{align}$
Perhatikan segitiga ADG siku-siku di titik D dengan pythagoras maka:
$\begin{align}AG &= \sqrt{AD^2+DG^2} \\ &= \sqrt{t^2+\left( \frac{1}{2}s\sqrt{3} \right)^2} \\ AG &= \sqrt{t^2+\frac{3s^2}{4}} \end{align}$
Jawaban: B
Soal No. 5
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P, Q, dan R berturut-turut terletak pada pertengahan garis AB, BC, dan bidang ADHE. Tentukan jarak dari titik P ke titik R dan jarak dari titik Q ke titik R.Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
AH diagonal sisi kubus, maka:
$AH=s\sqrt{2}=6\sqrt{2}$
$AR=\frac{1}{2}AH=\frac{1}{2}.6\sqrt{2}=3\sqrt{2}$
Segitiga RAP siku-siku di titik A, maka:
$\begin{align}PR &= \sqrt{AP^2+AR^2} \\ &= \sqrt{3^2+ \left( 3\sqrt{2} \right)^2} \\ &= \sqrt{9+18} \\ &= \sqrt{27} \\ PR &= 3\sqrt{3} \end{align}$
Jadi, jarak titik P ke R adalah $3\sqrt{3}$ cm.
Perhatikan segitiga RSQ siku-siku di titik S, maka:
$\begin{align}QR &= \sqrt{RS^2+SQ^2} \\ &= \sqrt{3^2+6^2} \\ &= \sqrt{9+36} \\ &= \sqrt{45} \\ QR &= 3\sqrt{5} \end{align}$
Jadi, jarak titik Q ke titik R adalah $3\sqrt{5}$ cm.
Soal No. 6
Diketahui balok ABCD.EFGH dengan AB = 12 cm, BC = 3 cm, dan AE = 4 cm, maka jarak titik D ke titik F adalah ... cm(A) 10
(B) 12
(C) 13
(D) 14
(E) 15
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Perhatikan segitiga DAB siku-siku di titik A, maka:
$\begin{align}BD^2 &= AB^2+AD^2 \\ &= 12^2+3^2 \\ BD^2 &= 153 \end{align}$
Perhatikan segitiga DBF siku-siku di titik B, maka:
$\begin{align}DF &= \sqrt{BD^2+BF^2} \\ &= \sqrt{153+4^2} \\ &= \sqrt{169} \\ DF &= 13 \end{align}$
Jadi, jarak titik D ke titik F adalah 13 cm.
Cara alternatif:
DF adalah diagonal ruang balok, maka:
$\begin{align}DF &= \sqrt{p^2+l^2+t^2} \\ &= \sqrt{12^2+3^2+4^2} \\ &= \sqrt{169} \\ DF &= 13 \end{align}$
Jawaban: C
Soal No. 7
Diketahui kubus PQRS.TUVW dengan rusuk $6\sqrt{2}$ cm, maka jarak titik R ke titik W adalah ... cm(A) 10
(B) 12
(C) 13
(D) 14
(E) 15
Penyelesaian: Lihat/Tutup
Perhatikan gambar!
Perhatikan segitiga WSR siku-siku di titik S, maka:
$\begin{align}WR &= \sqrt{WS^2+SR^2} \\ &= \sqrt{\left( 6\sqrt{2} \right)^2+ \left( 6\sqrt{2} \right)^2} \\ &= \sqrt{72+72} \\ &= \sqrt{144} \\ WR &= 12 \end{align}$
Jadi, jarak titik W ke titik R adalah 12 cm.
Cara alternatif:
WR adalah diagonal sisi kubus, maka:
$WR=s\sqrt{2}=6\sqrt{2}.\sqrt{2}=12$
Jawaban: B
Soal No. 8
Diberikan balok ABCD.EFGH dengan AB = 2BC = 2AE = 2 cm. Panjang AH adalah .. cm.(A) $\frac{1}{2}$
(B) 1
(C) $\sqrt{2}$
(D) 2
(E) $\sqrt{3}$
Penyelesaian: Lihat/Tutup
AB = 2BC = 2AE = 2 cmAB = 2 cm, BC = 1 cm, AE =1 cm
Perhatikan gambar berikut!

Segitiga ADH siku-siku di titik D, maka:
$\begin{align}AH &= \sqrt{AD^2+DH^2} \\ &= \sqrt{1^2+1^2} \\ AH &= \sqrt{2} \end{align}$
Jawaban: C
Soal No. 9
Diberikan kubus ABCD.EFGH dengan panjang rusuk 3p. Titik-titik P, Q dan R masing-masing pada FB, FG, dan AD sehingga BP = GQ = DR = p. Jika S adalah titik potong bidang yang melalui P, Q dan R dengan rusuk DH, maka jarak S ke P adalah ...(A) $3p\sqrt{2}$
(B) $\frac{3p}{\sqrt{2}}$
(C) $\frac{3}{2}p\sqrt{3}$
(D) $p^2\sqrt{19}$
(E) $p^2\sqrt{10}$
Penyelesaian: Lihat/Tutup
Perpanjang garis PQ dan garis CG sehingga berpotongan di titik K.Perpanjang garis QP dan garis CB sehingga berpotongan di titik L.
Lukis dan perpanjang garis LR dan garis CD sehingga berpotongan di titik N.
Lukis garis NK, akhirnya diperoleh perluasan dari bidang PQR yaitu KLN dan bidang KLN memotong garis DH di titik S.
Hasilnya adalah seperti gambar berikut ini!

BD diagonal sisi kubus maka:
$BD=s\sqrt{2}=3p\sqrt{2}$.
Jarak titik S ke titik P adalah SP.
$SP=BD=3p\sqrt{2}$
Jawaban: A
Soal No. 10
Prisma tegak segitiga sama sisi ABC.DEF dengan panjang AB = 4 cm dan AD = 6 cm. Jika titik G terletak di tengah-tengah sisi EF, maka panjang AG adalah ... cm.(A) $2\sqrt{3}$
(B) $4\sqrt{3}$
(C) $2\sqrt{6}$
(D) $3\sqrt{6}$
(E) $4\sqrt{6}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar!
$GF=\frac{1}{2}EF=2$
DG adalah garis tinggi segitiga DEF, maka:
$\begin{align}DG &= \sqrt{DF^2-GF^2} \\ &= \sqrt{4^2-2^2} \\ &= \sqrt{16-4} \\ &= \sqrt{12} \\ DG &= 2\sqrt{3} \end{align}$
Perhatikan segitiga ADG siku-siku di titik D dengan pythagoras maka:
$\begin{align}AG &= \sqrt{AD^2+DG^2} \\ &= \sqrt{6^2+\left( 2\sqrt{3} \right)^2} \\ &= \sqrt{36+12} \\ &= \sqrt{48} \\ AG &= 4\sqrt{3} \end{align}$
Jawaban: B
Soal No. 11
Sebuah kubus ABCD.EFGH dengan panjang sisi 6 cm, dan titik P merupakan titik potong diagonal EG dan FH. Jarak antara titik B dan titik P adalah ... cm.(A) $4\sqrt{2}$
(B) $3\sqrt{6}$
(C) $3\sqrt{2}$
(D) 3
(E) $2\sqrt{3}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Jarak antara titik B dan titik P adalah BP.
FH adalah diagonal sisi kubus, maka:
$FH=s\sqrt{2}=6\sqrt{2}$
Titik P di tengah FH, maka:
$\begin{align}FP &= \frac{1}{2}.FH \\ &= \frac{1}{2}.6\sqrt{2} \\ FP &= 3\sqrt{2} \end{align}$
Segitiga BFP siku-siku di F, maka:
$\begin{align}BP &= \sqrt{BF^2+FP^2} \\ &= \sqrt{6^2+\left( 3\sqrt{2} \right)^2} \\ &= \sqrt{36+18} \\ &= \sqrt{54} \\ BP &= 3\sqrt{6} \end{align}$
Jadi, jarak antara titik B dan titik P adalah $3\sqrt{6}$ cm.
Jawaban: B
Soal No. 12
Panjang setiap rusuk bidang empat beraturan D.ABC adalah 16 cm. Jika P pertengahan DA dan Q pertengahan BC maka panjang PQ adalah ... cm.(A) $3\sqrt{6}$
(B) $8\sqrt{3}$
(C) $8\sqrt{2}$
(D) $12\sqrt{3}$
(E) $12\sqrt{2}$
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Perhatikan segitiga DQC siku-siku di titik Q maka:
$\begin{align}DQ &= \sqrt{DC^2-QC^2} \\ &= \sqrt{16^2-8^2} \\ &= \sqrt{256-64} \\ &= \sqrt{192} \\ DQ &= 8\sqrt{3} \end{align}$
Perhatikan segitiga ABC, karena AB = AC dan titik Q membagi dua sama panjang sisi BC, maka $AQ\bot BC$
Perhatikan segitiga BQA siku-siku di titik Q maka:
$\begin{align}AQ &= \sqrt{AB^2-BQ^2} \\ &= \sqrt{16^2-8^2} \\ &= \sqrt{256-64} \\ &= \sqrt{192} \\ AQ &= 8\sqrt{3} \end{align}$
Perhatikan segitiga DAQ, karena AQ = DQ dan titik P di tengah AD maka $DQ\bot AD$.
Segitiga APQ siku-siku di titik P maka:
$\begin{align}PQ &= \sqrt{AQ^2-AP^2} \\ &= \sqrt{\left( 8\sqrt{3} \right)^2-8^2} \\ &= \sqrt{192-64} \\ &= \sqrt{128} \\ PQ &= 8\sqrt{2} \end{align}$
Jadi, panjang PQ adalah $8\sqrt{2}$ cm.
Jawaban: C

Post a Comment for "Soal Jarak Titik ke Titik pada Dimensi Tiga dan Pembahasan"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.