Persamaan dan Pertidaksamaan Irasional

A. Definisi Persamaan Irasional

Persamaan irasional adalah persamaan yang variabelnya berada di bawah tanda akar dan tidak dapat ditarik keluar tanda akar. Untuk semesta bilangan real, persamaan irasional terdefinisi jika komponen yang memuat variabel di bawah tanda akar bernilai lebih dari atau sama dengan nol.
Contoh:

1. $\sqrt{x+2} = 5$
2. $\sqrt{5x-1} = \sqrt{3-2x}$
3. $\sqrt{2x+3} = x$

B. Menentukan Penyelesaian Persamaan Irasional

Langkah-langkah menyelesaikan persamaan irasional secara umum adalah sebagai berikut:

1. Syarat terdefinisi yaitu di bawah tanda akar $\ge 0$.
2. Solusi (kuadratkan kedua ruas).
3. Tuliskan himpunan penyelesaian (HP).

Berikut ini beberapa bentuk umum persamaan irasional dan cara menyelesaikannya.

a) Bentuk $\sqrt{f(x)}=c$ dengan $c\ge 0$ dan syarat $f(x)\ge 0$.

Contoh 1.
Tentukan nilai $x$ yang memenuhi persamaan $\sqrt{x+2}=5$.
Penyelesaian:
$\sqrt{x+2} = 5\Leftrightarrow \sqrt{f(x)} = c$
1) Syarat:
$\begin{align}f(x) &\ge 0 \\ x+2 &\ge 0 \\ x &\ge -2 \end{align}$
2) Solusi (kuadratkan kedua ruas)
$\begin{align}\sqrt{x+2} &= 5 \\ x+2 &= 5^2 \\ x+2 &= 25 \\ x &= 23\,(\text{memenuhi}\,\text{syarat}) \end{align}$
3) HP = {23}

b) Bentuk $\sqrt{f(x)}=\sqrt{g(x)}$ dengan syarat $f(x)\ge 0\cap g(x)\ge 0$.

Contoh 2.
Tentukan nilai $x$ yang memenuhi persamaan $\sqrt{5x-1}=\sqrt{3-2x}$.
Penyelesaian:
$\sqrt{5x-1}=\sqrt{3-2x}\Leftrightarrow \sqrt{f(x)}=\sqrt{g(x)}$
1) Syarat:
$\begin{align}f(x) &\ge 0 \\ 5x-1 &\ge 0 \\ 5x &\ge 1 \\ x &\ge \frac{1}{5} \end{align}$
$\begin{align}g(x) &\ge 0 \\ 3-2x &\ge 0 \\ -2x &\ge -3 \\ x &\le \frac{3}{2} \end{align}$
$f(x)\ge 0\cap g(x)\ge 0$ = $\frac{1}{5}\le x\le \frac{3}{2}$.
2) Solusi (kuadratkan kedua ruas)
$\begin{align}\sqrt{5x-1} &= \sqrt{3-2x} \\ 5x-1 &= 3-2x \\ 7x &= 4 \\ x &= \frac{4}{7}\,(\text{memenuhi}\,\text{syarat}) \end{align}$
3) HP = $\left\{ \frac{4}{7} \right\}$

c) Bentuk $\sqrt{f(x)}=g(x)$ dengan syarat $f(x)\ge 0\cap g(x)\ge 0$.

Contoh 3.
Tentukan nilai $x$ yang memenuhi persamaan $\sqrt{2x+3}=x$.
Penyelesaian:
1) Syarat:
$\begin{align}f(x) &\ge 0 \\ 2x+3 &\ge 0 \\ 2x &\ge -3 \\ x &\ge -\frac{3}{2} \end{align}$
$\begin{align}g(x) &\ge 0 \\ x &\ge 0 \end{align}$
$f(x)\ge 0\cap g(x)\ge 0$ = $x\ge 0$.
2) Solusi (kuadratkan kedua ruas)
$\begin{align}\sqrt{2x+3} &= x \\ 2x+3 &= x^2 \\ x^2-2x-3 &= 0 \\ (x+1)(x-3) &= 0 \end{align}$
$x=-1$ (tidak memenuhi syarat)
$x=3$ (memenuhi syarat)
3) HP = {3}

C. Menentukan Penyelesaian Pertidaksamaan Irasional

Langkah-langkah menyelesaikan pertidaksamaan irasional secara umum adalah sebagai berikut:

1. Syarat terdefinisi yaitu di bawah tanda akar $\ge 0$.
2. Kuadratkan kedua ruas.
3. Tuliskan pada garis bilangan hasil pada langkah 1) dan 2), kemudian arsir daerah irisannya.
4. Tuliskan himpunan penyelesaian (HP) yaitu interval daerah irisan.

Berikut ini beberapa bentuk umum pertidaksamaan irasional dan cara menyelesaikannya.

a) Bentuk $\sqrt{f(x)} \ge c$ dengan $c \ge 0$
Solusi:
1) $f(x) \ge 0$
2) $\left( \sqrt{f(x)} \right)^2\ge c^2$

Contoh 4.
Tentukan nilai $x$ yang memenuhi pertidaksamaan $\sqrt{5-2x}>9$.
Penyelesaian:
$\sqrt{5-2x} > 9 \Leftrightarrow \sqrt{f(x)} > c$
1) $f(x) \ge 0$ maka:
$\begin{align}5-2x &\ge 0 \\ -2x &\ge -5 \\ x &\le \frac{5}{2} \end{align}$
2) $\left( \sqrt{f(x)} \right)^2 \ge c^2$ maka:
$\begin{align}\left( \sqrt{5-2x} \right)^2 &> 9^2 \\ 5-2x &> 81 \\ -2x &> 76 \\ x &< -38 \end{align}$
3) Garis bilangan:

4) Himpunan penyelesaian (HP) = {$x<-38$}

b) Bentuk $\sqrt{f(x)} \ge c$ dengan $c<0$.
Solusi: $f(x) \ge 0$.

Contoh 5.
Tentukan nilai $x$ yang memenuhi pertidaksamaan $\sqrt{x^2-3x-10} > -3$.
Penyelesaian:
$\sqrt{x^2-3x-10} > -3 \Leftrightarrow \sqrt{f(x)} > c$; $c = -3 \Leftrightarrow c < 0$
$\begin{align}f(x) &\ge 0 \\ x^2-3x-10 &\ge 0 \\ (x+2)(x-5) &\ge 0 \end{align}$
$x\le -2$ atau $x\ge 5$
HP = {$x\le -2$ atau $x\ge 5$}

c) Bentuk $\sqrt{f(x)}\le c$ dengan $c\ge 0$
Solusi:
1) $f(x) \ge 0$
2) $\left( \sqrt{f(x)} \right)^2 \le c^2$

Contoh 6.
Tentukan nilai $x$ yang memenuhi pertidaksamaan $\sqrt{5x-1} \le 3$.
Penyelesaian:
$\sqrt{5x-1} \le 3\Leftrightarrow \sqrt{f(x)} \le c$
1) $f(x) \ge 0$ maka:
$\begin{align}5x-1 &\ge 0 \\ 5x &\ge 1 \\ x &\ge \frac{1}{5} \end{align}$
2) $\left( \sqrt{f(x)} \right)^2 \le c^2$ maka:
$\begin{align}\left( \sqrt{5x-1} \right)^2 &\le 3^2 \\ 5x &\le 10 \\ x &\le 2 \end{align}$
3) Garis bilangan:

4) Himpunan penyelesaian (HP) = $\frac{1}{5} \le x \le 2$

d) Bentuk $\sqrt{f(x)} \le c$ dengan $c < 0$
Solusi: HP = {}.

Contoh 7.
Tentukan nilai $x$ yang memenuhi pertidaksamaan $\sqrt{7x-1} < -4$.
Penyelesaian:
$\sqrt{7x-1} < -4 \Leftrightarrow \sqrt{f(x)} \le c$; $c = -4 \Leftrightarrow c < 0$
HP = { }

e) Bentuk $\sqrt{f(x)} \le \sqrt{g(x)}$
Solusi:
1) $f(x) \ge 0$
2) $g(x) \ge 0$
3) $\left( \sqrt{f(x)} \right)^2 \le \left( \sqrt{g(x)} \right)^2$

Contoh 8.
Tentukan nilai $x$ yang memenuhi pertidaksamaan $\sqrt{6-x} < \sqrt{2x+8}$.
Penyelesaian:
$\sqrt{6-x} < \sqrt{2x+8} \Leftrightarrow \sqrt{f(x)} \le \sqrt{g(x)}$
1) $f(x) \ge 0$ maka:
$\begin{align}6-x &\ge 0 \\ -x &\ge -6 \\ x &\le 6 \end{align}$
2) $g(x) \ge 0$ maka:
$\begin{align}2x+8 &\ge 0 \\ 2x &\ge -8 \\ x &\ge -4 \end{align}$
3) $\left( \sqrt{f(x)} \right)^2 < \left( \sqrt{g(x)} \right)^2$ maka:
$\begin{align}\left( \sqrt{6-x} \right)^2 &< \left( \sqrt{2x+8} \right)^2 \\ 6-x &< 2x+8 \\ -3x &< 2 \\ x &> -\frac{2}{3} \end{align}$
4) Garis bilangan:

5) Himpunan penyelesaian (HP) = $\left\{ -\frac{2}{3} < x \le 6 \right\}$.

f) Bentuk $\sqrt{f(x)} \ge \sqrt{g(x)}$
Solusi:
1) $f(x) \ge 0$
2) $g(x) \ge 0$
3) $\left( \sqrt{f(x)} \right)^2 \ge \left( \sqrt{g(x)} \right)^2$

Contoh 9.
Tentukan nilai $x$ yang memenuhi pertidaksamaan $\sqrt{2x+1} > \sqrt{3-x}$.
Penyelesaian:
1) $f(x) \ge 0$ maka:
$\begin{align}2x+1 &\ge 0 \\ 2x &\ge -1 \\ x &\ge -\frac{1}{2} \end{align}$
2) $g(x) \ge 0$ maka:
$\begin{align}3-x &\ge 0 \\ -x &\ge -3 \\ x &\le 3 \end{align}$
3) $\left( \sqrt{f(x)} \right)^2 > \left( \sqrt{g(x)} \right)^2$ maka:
$\begin{align}\left( \sqrt{2x+1} \right)^2 &> \left( \sqrt{3-x} \right)^2 \\ 2x+1 &> 3-x \\ 3x &> 2 \\ x &> \frac{2}{3} \end{align}$
4) Garis bilangan:

5) Himpunan penyelesaian (HP) = $\left\{ x | \frac{2}{3} < x \le 3 \right\}$.

g) Bentuk $\sqrt{f(x)} \le g(x)$
Solusi:
1) $f(x) \ge 0$
2) $g(x) \ge 0$
3) $\left( \sqrt{f(x)} \right)^2 \le \left( g(x) \right)^2$

Contoh 10.
Tentukan nilai $x$ yang memenuhi pertidaksamaan $5x+\sqrt{10x-25} < 20$.
Penyelesaian:
$\begin{align}5x+\sqrt{10x-25} &< 20 \\ \sqrt{10x-25} &< 20-5x \\ \sqrt{f(x)} &< g(x) \end{align}$
1) $f(x)\ge 0$ maka:
$\begin{align}10x-25 &\ge 0 \\ 10x &\ge 25 \\ x &\ge \frac{25}{10} \\ x &\ge \frac{5}{2} \end{align}$
2) $g(x) \ge 0$ maka:
$\begin{align}20-5x &\ge 0 \\ -5x &\ge -20 \\ x &\le 4 \end{align}$
3) $\left( \sqrt{f(x)} \right)^2 < \left( g(x) \right)^2$ maka:
$\begin{align}\left( \sqrt{10x-25} \right)^2 &< \left( 20-5x \right)^2 \\ 10x-25 &< 400-200x+25x^2 \\ -25x^2+210x-425 &< 0 \\ 5x^2-42x+85 &> 0 \\ (5x-17)(x-5) &> 0 \end{align}$
$x < \frac{17}{5}$ atau $x > 5$
4) Garis bilangan:

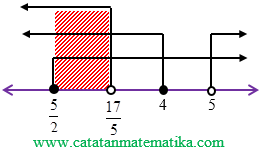
5) Himpunan penyelesaian (HP) = $\left\{ x | \frac{5}{2} \le x < \frac{17}{5} \right\}$.

h) Bentuk $\sqrt{f(x)} \ge g(x)$.
Solusi 1:
1) $f(x) \ge 0$
2) $g(x) \ge 0$
3) $\left( \sqrt{f(x)} \right)^2 \ge \left( g(x) \right)^2$
Solusi 2:
1) $f(x) \ge 0$
2) $g(x) < 0$ HP = Solusi 1 atau solusi 2

Contoh 11.
Semua nilai $x$ yang memenuhi $\sqrt{x^2-7x+6} > 2x$ adalah ...
Penyelesaian:
$\sqrt{x^2-7x+6} > 2x \Leftrightarrow \sqrt{f(x)} > g(x)$
Solusi 1:
1) $f(x)\ge 0$ maka:
$\begin{align}x^2-7x+6 &\ge 0 \\ (x-1)(x-6) &\ge 0 \end{align}$
$x \le 1$ atau $x \ge 6$
2) $g(x) \ge 0$ maka:
$\begin{align}2x &\ge 0 \\ x &\ge 0 \end{align}$
3) $\left( \sqrt{f(x)} \right)^2 > \left( g(x) \right)^2$ maka:
$\begin{align}\left( \sqrt{x^2-7x+6} \right)^2 & > \left( 2x \right)^2 \\ x^2-7x+6 & > 4x^2 \\ -3x^2-7x+6 & > 0 \\ 3x^2+7x-6 & < 0 \\ (3x-2)(x+3) & < 0 \end{align}$
$-3 < x < \frac{2}{3}$
4) Garis bilangan:

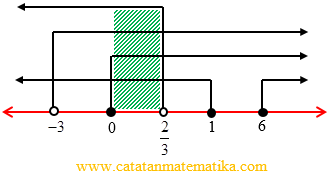
5) $HP_1$ = $\left\{ x|0 \le x < \frac{2}{3} \right\}$.

Solusi 2:
1) $f(x)\ge 0$ maka:
$\begin{align}x^2-7x+6 &\ge 0 \\ (x-1)(x-6) &\ge 0 \end{align}$
$x \le 1$ atau $x \ge 6$
2) $g(x) < 0$ maka:
$\begin{align}2x & < 0 \\ x & < 0 \end{align}$
3) Garis bilangan:

4) $HP_2$ = $\left\{ x|x < 0 \right\}$
5) Himpunan penyelesaian (HP) = $HP_1 \cup HP_2$

HP = $\left\{ x < \frac{2}{3} \right\}$

D. Soal Latihan

Tentukan nilai $x$ yang memenuhi persamaan dan pertidaksamaan berikut ini.

1. $\sqrt{5-x} \ge 7$.
2. $\sqrt{x^2-2x-8} > 4$
3. $\sqrt{4x-1} \ge -2$
4. $\sqrt{3x-1} < 1$
5. $\sqrt{x^2-x-56} < 4$
6. $\sqrt{5x-2} < -3$
7. $\sqrt{x+6} \le \sqrt{2x+3}$
8. $\sqrt{4x+1} > \sqrt{7-x}$
9. $\sqrt{3x+6} > x$
10. $x+\sqrt{x-1} < 7$

Semoga postingan: Persamaan dan Pertidaksamaan Irasional ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :