Persamaan dan Pertidaksamaan Rasional

A. Definisi Persamaan Rasional

Persamaan rasional adalah persamaan dalam bentuk pecahan yang memuat satu atau lebih variabel pada pembilang atau penyebut.
Bentuk umum: $\frac{f(x)}{g(x)} = 0$.

B. Menentukan Penyelesaian Persamaan Rasional

Cara menentukan penyelesaian persamaan rasional:

1. Nolkan ruas kanan.
2. Faktorkan pembilang dan penyebut.
3. Tentukan syarat penyelesaian yaitu penyebut tidak sama dengan nol.
4. Tentukan penyelesaian yaitu penyebut sama dengan nol dan memenuhi syarat pada langkah 3.
5. Tuliskan HP.

Contoh 1.

Tentukan himpunan penyelesaian dari persamaan $\frac{x+2}{4} = \frac{3}{2x-6}$.
Penyelesaian:
$\begin{align}\frac{x+2}{4} &= \frac{3}{2x-6} \\ \frac{x+2}{4}-\frac{3}{2x-6} &= 0 \\ \frac{(x+2)(2x-6)-3.4}{4(2x-6)} &= 0 \\ \frac{2x^2-6x+4x-12-12}{8x-24} &= 0 \\ \frac{2x^2-2x-24}{8x-24} &= 0 \\ \frac{2(x^2-x-12)}{8(x-3)} &= 0 \\ \frac{(x-4)(x+3)}{4(x-3)} &= 0 \end{align}$
Syarat:
$\begin{align}x-3 &\ne 0 \\ x &\ne 3 \end{align}$
Solusi:
$x-4=0\Leftrightarrow x = 4$ (memenuhi syarat)
$x+3=0\Leftrightarrow x = -3$ (memenuhi syarat)
HP = {-3, 4}

Contoh 2.

Nilai $x$ yang memenuhi persamaan $\frac{4x-5}{x} = x-2$ adalah ...
Penyelesaian:
$\begin{align}\frac{4x-5}{x} &= x-2 \\ \frac{4x-5}{x}-(x-2) &= 0 \\ \frac{4x-5}{x}-\frac{x(x-2)}{x} &= 0 \\ \frac{4x-5}{x}-\frac{x^2-2x}{x} &= 0 \\ \frac{-x^2+6x-5}{x} &= 0 \\ \frac{x^2-6x+5}{x} &= 0 \\ \frac{(x-1)(x-5)}{x} &= 0 \end{align}$
Syarat:
$x\ne 0$
Solusi:
$x-1 = 0 \Leftrightarrow x = 1$ (memenuhi syarat)
$x-5 = 0 \Leftrightarrow x = 5$ (memenuhi syarat)
HP = {1, 5}

Contoh 3.

Nilai $x$ yang memenuhi persamaan $\frac{x^2-9x}{x+3} = \frac{36}{x+3}$ adalah ...
Penyelesaian:
$\begin{align}\frac{x^2-9x}{x+3} &= \frac{36}{x+3} \\ \frac{x^2-9x}{x+3}-\frac{36}{x+3} &= 0 \\ \frac{x^2-9x-36}{x+3} &= 0 \\ \frac{(x-12)(x+3)}{x+3} &= 0 \\ \end{align}$
Syarat:
$x+3 = 0 \Leftrightarrow x = -3$
Solusi:
$x-12 = 0 \Leftrightarrow x = 12$ (memenuhi syarat)
$x+3 = 0 \Leftrightarrow x = -3$ (tidak memenuhi syarat).
HP = {12}

Contoh 4.

Nilai $a$ yang memenuhi persamaan $\frac{3}{a}-\frac{2a}{a-3} = \frac{11}{2}$ adalah ...
Penyelesaian:
$\begin{align}\frac{3}{a}-\frac{2a}{a-3} &= \frac{11}{2} \\ \frac{3}{a}-\frac{2a}{a-3}-\frac{11}{2} &= 0 \\ \frac{3.2(a-3)-2a.2a-11.a(a-3)}{2a(a-3)} &= 0 \\ \frac{6a-18-4a^2-11a^2+33a}{2a(a-3)} &= 0 \\ \frac{-15a^2+39a-18}{2a(a-3)} &= 0 \\ \frac{-3(5a^2-13a+6)}{2a(a-3)} &= 0 \\ \frac{-3(5a-3)(a-2)}{2a(a-3)} &= 0 \end{align}$
Syarat:
$a \ne 0$ dan $a-3 \ne 0\Leftrightarrow a\ne 3$
Solusi:
$5a-3 = 0 \Leftrightarrow a = \frac{3}{5}$ (memenuhi syarat)
$a-2 = 0 \Leftrightarrow a = 2$ (memenuhi syarat)
HP = $\left\{ \frac{3}{5},2 \right\}$

Contoh 5.

Himpunan penyelesaian dari persamaan $\frac{x}{x-2}-\frac{7}{x+2} = \frac{8}{x^2-4}$ adalah ....
Penyelesaian:
$\begin{align}\frac{x}{x-2}-\frac{7}{x+2} &= \frac{8}{x^2-4} \\ \frac{x(x+2)-7(x-2)}{(x-2)(x+2)} &= \frac{8}{(x-2)(x+2)} \\ \frac{x^2+2x-7x+14}{(x-2)(x+2)} &= \frac{8}{(x-2)(x+2)} \\ \frac{x^2-5x+6}{(x-2)(x+2)} &= 0 \\ \frac{(x-2)(x-3)}{(x-2)(x+2)} &= 0 \end{align}$
Syarat:
$x-2 \ne 0 \Leftrightarrow x \ne 2$
$x+2 \ne 0 \Leftrightarrow x \ne -2$
Solusi:
$x-2 = 0\Leftrightarrow x = 2$ (tidak memenuhi syarat)
$x-3 = 0\Leftrightarrow x = 3$ (memenuhi syarat).
HP = {3}

C. Pertidaksamaan Rasional

Pertidaksamaan rasional adalah pertidaksamaan yang variabelnya termuat dalam bentuk pecahan.
Bentuk umum:
$\frac{f(x)}{g(x)} < 0$; $\frac{f(x)}{g(x)} \le 0$; $\frac{f(x)}{g(x)} > 0$; $\frac{f(x)}{g(x)} \ge 0$

Langkah-langkah umum menyelesaikan pertidaksamaan rasional adalah:

1. Nolkan ruas kanan.
2. Faktorkan pembilang dan penyebut menjadi faktor-faktor linear.
3. Tentukan pembuat nol.
4. Tulis pembuat nol pada garis bilangan.
5. Tentukan daerah-daerah yang dibatasi oleh pembuat nol.
6. Ambil masing-masing satu titik pada setiap daerah dan uji ke pertidaksamaan, dan tulis mana daerah yang memenuhi dan yang tidak memenuhi.
7. Arsir daerah yang memenuhi.
8. Tuliskan HP.

Contoh 1.

Tentukan himpunan penyelesaian dari $\frac{2-x}{x+1} < 0$.
Penyelesaian:
$\frac{2-x}{x+1} < 0$
Pembuat nol:
Pembilang: $2-x = 0 \Leftrightarrow x = 2$
Penyebut: $x+1 = 0 \Leftrightarrow x = -1$
Garis bilangan:
Pada titik $x = 2$ kita tuliskan bulatan kosong karena pada soal tidak memuat tanda sama dengan (=).
Pada titik $x = -1$ kita tuliskan bulatan kosong karena diperoleh dari penyebut.

Garis bilangan terbagi menjadi 3 daerah yaitu: $x < -1$, $-1< x < 2$, dan $x > 2$.
Ambil masing-masing satu titik uji dari setiap daerah, kemudian uji ke pertidaksamaan $\frac{2-x}{x+1} < 0$.
Untuk daerah $x<-1$ ambil $x=-2$
$\begin{align}\frac{2-x}{x+1} &< 0 \\ \frac{2-(-2)}{(-2)+1} &< 0 \\ -4 < 0 \end{align}$
(memenuhi = M)

Untuk daerah $-1 < x < 2$ ambil $x = 0$
$\begin{align}\frac{2-x}{x+1} &< 0 \\ \frac{2-0}{0+1} &< 0 \\ 2 &< 0 \end{align}$
(tidak memenuhi = TM)

Untuk daerah $x > 2$ ambil $x=3$
$\begin{align}\frac{2-x}{x+1} &< 0 \\ \frac{2-3}{3+1} &< 0 \\ -\frac{1}{4} &< 0 \end{align}$
(memenuhi = M)

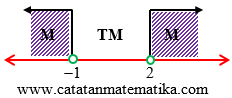
HP = {$x < -1$ atau $x > 2$}

Contoh 2.

Tentukan himpunan penyelesaian dari $\frac{x-3}{x+7} \ge 1$.
Penyelesaian:
$\begin{align}\frac{x-3}{x+7} &\ge 1 \\ \frac{x-3}{x+7}-1 &\ge 0 \\ \frac{x-3}{x+7}-\frac{x+7}{x+7} &\ge 0 \\ \frac{-10}{x+7} &\ge 0 \end{align}$
Pembuat nol:
Pada penyebut: $x+7 = 0 \Leftrightarrow x = -7$
Garis bilangan:
Pada titik $x = -7$ tuliskan bulatan kosong karena diperoleh dari penyebut.

Garis bilangan terbagi menjadi 2 daerah yaitu: $x < -7$ dan $x > -7$.
Ambil masing-masing satu titik uji dari setiap daerah, kemudian uji ke pertidaksamaan $\frac{x-3}{x+7} \ge 1$.
Untuk daerah $x < -7$ ambil $x = -8$
$\begin{align}\frac{x-3}{x+7} &\ge 1 \\ \frac{-8-3}{-8+7} &\ge 1 \\ 11 &\ge 1 \end{align}$
(memenuhi = M)

Untuk daerah $x > -7$ ambil $x = -6$
$\begin{align}\frac{x-3}{x+7} &\ge 1 \\ \frac{-6-3}{-6+7} &\ge 1 \\ -9 &\ge 1 \end{align}$
(tidak memenuhi = TM)

HP = {$x < -7$}

Contoh 3.

Tentukan himpunan penyelesaian dari $\frac{2x^2+2x-4}{x^2+4} \le 1$.
Penyelesaian:
$\begin{align}\frac{2x^2+2x-4}{x^2+4} &\le 1 \\ \frac{2x^2+2x-4}{x^2+4}-1 &\le 0 \\ \frac{2x^2+2x-4}{x^2+4}-\frac{x^2+4}{x^2+4} &\le 0 \\ \frac{x^2+2x-8}{x^2+4} &\le 0 \\ \frac{(x+4)(x-2)}{x^2+4} &\le 0 \end{align}$
Pembuat nol:
Pembilang:
$x+4 = 0 \Leftrightarrow x = -4$
$x-2 = 0 \Leftrightarrow x = 2$
Penyebut: $x^2+4$ tidak ada nilai $x$ pembuat nol karena definit, hal ini dapat dilihat berdasarkan nilai diskrimannya ($D < 0$):
$\begin{align}D &= b^2-4ac \\ &= 0^2-4.1.4 \\ D &= -16 \end{align}$
Garis bilangan:
Pada titik $x = -4$ dan $x = 2$ kita tuliskan bulatan penuh karena memuat tanda sama dengan (=).

Garis bilangan terbagi menjadi 3 daerah yaitu: $x \le -4$, $-4 \le x \le 2$ dan $x \ge 2$.
Ambil masing-masing satu titik uji dari setiap daerah, kemudian uji ke pertidaksamaan $\frac{2x^2+2x-4}{x^2+4} \le 1$.
Untuk daerah $x \le -4$ ambil $x = -5$
$\begin{align}\frac{2x^2+2x-4}{x^2+4} &\le 1 \\ \frac{2(-5)^2+2(-5)-4}{(-5)^2+4} &\le 1 \\ \frac{36}{29} &\le 1 \end{align}$
(tidak memenuhi = TM)

Untuk daerah $-4 \le x \le 2$ ambil $x = 0$
$\begin{align}\frac{2x^2+2x-4}{x^2+4} &\le 1 \\ \frac{2.0^2+2.0-4}{0^2+4} &\le 1 \\ -1 &\le 1 \end{align}$
(memenuhi = M)

Untuk daerah $x \ge 2$ ambil $x = 3$
$\begin{align}\frac{2x^2+2x-4}{x^2+4} &\le 1 \\ \frac{2.3^2+2.3-4}{3^2+4} &\le 1 \\ \frac{20}{13} &\le 1 \end{align}$
(tidak memenuhi = TM)

HP = {$-4 \le x \le 2$}

Contoh 4.

Tentukan himpunan penyelesaian dari $\frac{x-6}{x-3} > \frac{x-2}{x+1}$.
Penyelesaian:
$\frac{x-6}{x-3} > \frac{x-2}{x+1}$
$\frac{x-6}{x-3}-\frac{x-2}{x+1} > 0$
$\frac{(x-6)(x+1)-(x-2)(x-3)}{(x-3)(x+1)} > 0$
$\frac{x^2+x-6x-6-(x^2-3x-2x+6)}{(x-3)(x+1)} > 0$
$\frac{-12}{(x-3)(x+1)} > 0$
Pembuat nol:
Penyebut:
$x-3 = 0 \Leftrightarrow x = 3$
$x+1 = 0 \Leftrightarrow x = -1$
Garis bilangan:
Pada titik $x = -1$ dan $x = 3$ tuliskan bulatan kosong, karena diperoleh dari penyebut.

Garis bilangan terbagi menjadi tiga daerah yaitu: $x < -1$, $-1 < x < 3$, dan $x > 3$.
Ambil masing-masing satu titik uji dari setiap daerah, kemudian uji ke pertidaksamaan $\frac{x-6}{x-3} > \frac{x-2}{x+1}$.
Untuk daerah $x < -1$ ambil $x = -2$
$\begin{align}\frac{x-6}{x-3} &> \frac{x-2}{x+1} \\ \frac{-2-6}{-2-3} &> \frac{-2-2}{-2+1} \\ \frac{8}{5} &> 4 \end{align}$
(tidak memenuhi = TM)

Untuk daerah $-1 < x < 3$ ambil $x = 0$
$\begin{align}\frac{x-6}{x-3} &> \frac{x-2}{x+1} \\ \frac{0-6}{0-3} &> \frac{0-2}{0+1} \\ 2 &> -2 \end{align}$
(memenuhi = M)

Untuk daerah $x > 3$ ambil $x = 4$
$\begin{align}\frac{x-6}{x-3} &> \frac{x-2}{x+1} \\ \frac{4-6}{4-3} &> \frac{4-2}{4+1} \\ -2 &> \frac{2}{5} \end{align}$
(tidak memenuhi = TM).

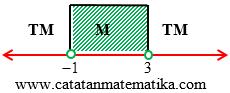
HP = {$-1 < x < 3$}

Contoh 5.

Tentukan nilai $x$ agar grafik $y = \frac{3}{x}-2x$ terletak di atas garis $y = x$.
Penyelesaian:
$y_1 = \frac{3}{x}-2x$ di atas $y_1 = x$ maka:
$\begin{align}y_1 &> y_2 \\ \frac{3}{x}-2x &> x \\ \frac{3}{x}-3x &> 0 \\ \frac{3}{x}-\frac{x(3x)}{x} &> 0 \\ \frac{3-3x^2}{x} &> 0 \\ \frac{3(1-x^2)}{x} &> 0 \\ \frac{(1-x)(1+x)}{x} &> 0 \end{align}$
Pembuat nol:
Pembilang:
$1-x = 0 \Leftrightarrow x = 1$
$1+x = 0 \Leftrightarrow x = -1$
Penyebut:
$x = 0$
Garis bilangan:
Pada titik $x = 1$ dan $x = -1$ tuliskan bulatan kosong karena pertidaksamaan tidak memuat tanda sama dengan (=).
Pada titik $x=0$ tuliskan bulatan kosong karena diperoleh dari penyebut.

Garis bilangan terbagi menjadi 4 daerah yaitu: $x < -1$, $-1< x < 0$, $0 < x < 1$ dan $x > 1$.
Ambil masing-masing satu titik uji dari setiap daerah, kemudian uji ke pertidaksamaan $\frac{(1-x)(1+x)}{x} > 0$.
Untuk daerah $x < -1$ ambil $x = -2$
$\begin{align}\frac{(1-x)(1+x)}{x} &> 0 \\ \frac{(1+2)(1-2)}{-2} &> 0 \\ \frac{3}{2} &> 0 \end{align}$
(memenuhi = M)

Untuk daerah $-1 < x < 0 $ ambil $x = -\frac{1}{2}$
$\begin{align}\frac{(1-x)(1+x)}{x} &> 0 \\ \frac{\left( 1+\frac{1}{2} \right)\left( 1-\frac{1}{2} \right)}{-\frac{1}{2}} &> 0 \\ -\frac{3}{2} &> 0 \end{align}$
(tidak memenuhi = TM)

Untuk daerah $0 < x < 1 $ ambil $x = \frac{1}{2}$
$\begin{align}\frac{(1-x)(1+x)}{x} &> 0 \\ \frac{\left( 1-\frac{1}{2} \right)\left( 1+\frac{1}{2} \right)}{\frac{1}{2}} &> 0 \\ \frac{3}{2} &> 0 \end{align}$
(memenuhi = M)

Untuk daerah $x > 1$ ambil $x = 2$
$\begin{align}\frac{(1-x)(1+x)}{x} &> 0 \\ \frac{(1-2)(1+2)}{2} &> 0 \\ -\frac{3}{2} &> 0 \end{align}$
(tidak memenuhi = TM).

HP = {$x<-1$ atau $0 < x < 1$}

D. Soal Latihan

Tentukan himpunan penyelesaian dari persamaan dan pertidaksamaan rasional berikut ini.

1. $\frac{x}{2}+\frac{7-x}{3} = -\frac{1}{6}+x$
2. $\frac{x-4}{2x+1} = \frac{x-9}{x}$
3. $\frac{1}{x-4}-\frac{1}{x+6} = \frac{5}{28}$
4. $\frac{5x-8}{x-1} = \frac{14x+12}{3x+5}$
5. $\frac{14}{x^2-2x}-\frac{21}{x^2+2x} = \frac{5}{x}$
6. $\frac{x+3}{x-3} \ge 2$
7. $\frac{2x+1}{x-1} > 1$
8. $\frac{x+2}{x^2+2x-8} \ge 0$
9. $\frac{x^2-3x+1}{x^2+2x} \le \frac{-2}{x+2}$
10. $\frac{x-4}{x-3} \le \frac{x-3}{x-2}$

Semoga postingan: Persamaan dan Pertidaksamaan Rasional ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :