Statistika 3. Penyajian Data Dalam Bentuk Tabel Distibusi Frekuensi
Agar suatu data dapat dipahami dengan mudah, maka data harus disajikan secara ringkas dan jelas. Salah satu cara menyajikan data adalah dengan tabel distribusi frekuensi yaitu mengelompokkan data ke dalam beberapa kelompok (kelas) dan dihitung banyaknya (frekuensi) data yang masuk dalam kelompok tersebut serta hasilnya disusun dalam bentuk tabel.

Data di atas jika disajikan dalam tabel distribusi frekuensi sebagai berikut:

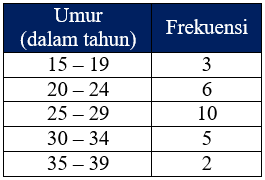
Untuk lebih memahami tabel distribusi frekuensi, berikut ini beberapa istilah yang harus kita pahami terlebih dahulu.
a) Kelas
Kelas adalah interval suatu data yang memuat beberapa data. Tabel di atas terdiri dari 5 kelas yaitu:
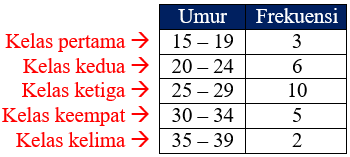
b) Batas kelas
Pada setiap kelas terdapat 2 batas kelas yaitu batas bawah (nilai terkecil pada kelas) dan batas atas (nilai terbesar pada kelas.
Untuk lebih jelasnya perhatikan tabel berikut:

c) Tepi kelas
Tepi kelas adalah setengah dari jumlah batas atas dan batas bawah dua kelas yang berurutan. Setiap kelas memiliki tepi atas dan tepi bawah. Untuk lebih jelasnya, berdasarkan tabel di atas, maka tepi bawah dan tepi atas kelas ketiga adalah:

d) Panjang kelas (c)
Panjang kelas adalah selisih antara tepi atas kelas dengan tepi bawah kelas.
$c=t_a-t_b$
Contoh: berdasarkan tabel di atas yaitu kelas ketiga (25-29) diperoleh $t_a$ = 29,5 dan $t_b$ = 24,5 maka:
$\begin{align}c &= t_a-t_b \\ &= 29,5-24,5 \\ c &= 5 \end{align}$
e) Titik tengah kelas ($x_i$)
Nilai titik tengah kelas adalah setengah dari jumlah batas bawah kelas dan batas atas kelas.
${{x}_{i}}=\frac{1}{2}\left( \text{Batas}\,\text{atas}+\text{Batas}\,\text{bawah} \right)$
Untuk lebih jelasnya perhatikan tabel berikut:

Contoh:
Data berikut adalah data jumlah pengunjung perpustakaan SMA NASIONAL dalam 40 hari kerja berturut-turut.

Sajikanlah data tersebut ke dalam tabel distribusi frekuensi data berkelompok.
Penyelesaian:
$x_{maks}=96$ dan $x_{min}=50$
$\begin{align}J &= x_{maks}-x_{min} \\ &= 96-50 \\ J &= 46 \end{align}$
Banyak kelas (k):
$\begin{align}k &= 1+(3,3)\log n \\ &= 1+(3,3).\log 40 \\ &= 1+(3,3)\times (1,6) \\ &= 1+5,28 \\ k &= 6,28 \end{align}$
Ingat dalam menentukan banyak kelas gunakan pembulatan ke atas. Jadi, k = 7.
Panjang kelas (c):
$\begin{align}c &= \frac{J}{k} \\ &= \frac{46}{7} \\ c &= 6,57 \end{align}$
Pembulatan ke atas, maka c = 7
Kemudian kita susun daftar distribusi frekuensi dengan menetapkan interval sehingga nilai minimum 50 termuat dalam kelas terendah dan nilai maksimum 96 termuat dalam kelas tertinggi. Selanjutnya menetapkan frekuensi tiap kelas. Hasilnya seperti tabel di bawah ini.

Atau dapat juga seperti tabel berikut:

Contoh:
Sajikanlah data berikut ini ke dalam tabel distribusi frekuensi kumulatif.

Penyelesaian:

Sajikan data di atas dalam tabel distribusi frekuensi data berkelompok, lengkap dengan frekuensi kumulatifnya.
A. Tabel Distribusi Frekuensi Data Tunggal
Berikut ini adalah nilai ulangan matematika kelas 5 SD
Data di atas jika disajikan dalam tabel distribusi frekuensi sebagai berikut:

B. Tabel Distribusi Frekuensi Data Berkelompok
Walaupun data tunggal yang kita peroleh sangat banyak, kita dapat mempersingkatnya dengan menyajikannya dalam tabel disribusi frekuensi secara berkelompok. Seperti tabel berikut ini:
Untuk lebih memahami tabel distribusi frekuensi, berikut ini beberapa istilah yang harus kita pahami terlebih dahulu.
a) Kelas
Kelas adalah interval suatu data yang memuat beberapa data. Tabel di atas terdiri dari 5 kelas yaitu:

b) Batas kelas
Pada setiap kelas terdapat 2 batas kelas yaitu batas bawah (nilai terkecil pada kelas) dan batas atas (nilai terbesar pada kelas.
Untuk lebih jelasnya perhatikan tabel berikut:

c) Tepi kelas
Tepi kelas adalah setengah dari jumlah batas atas dan batas bawah dua kelas yang berurutan. Setiap kelas memiliki tepi atas dan tepi bawah. Untuk lebih jelasnya, berdasarkan tabel di atas, maka tepi bawah dan tepi atas kelas ketiga adalah:

d) Panjang kelas (c)
Panjang kelas adalah selisih antara tepi atas kelas dengan tepi bawah kelas.
$c=t_a-t_b$
Contoh: berdasarkan tabel di atas yaitu kelas ketiga (25-29) diperoleh $t_a$ = 29,5 dan $t_b$ = 24,5 maka:
$\begin{align}c &= t_a-t_b \\ &= 29,5-24,5 \\ c &= 5 \end{align}$
e) Titik tengah kelas ($x_i$)
Nilai titik tengah kelas adalah setengah dari jumlah batas bawah kelas dan batas atas kelas.
${{x}_{i}}=\frac{1}{2}\left( \text{Batas}\,\text{atas}+\text{Batas}\,\text{bawah} \right)$
Untuk lebih jelasnya perhatikan tabel berikut:

C. Cara Menyusun Tabel Distribusi Frekuensi Data Berkelompok
Berikut ini langkah-langkah dalam membuat tabel distribusi frekuensi data berkelompok.
- Menentukan nilai data terbesar ($x_{maks}$) dan nilai data terkecil ($x_{min} $).
- Menentukan jangkauan data (J) dengan rumus: $J=x_{maks}-x_{min}$.
- Menentukan banyak kelas ($k$) dan $n$ buah data berdasarkan aturan sturgess, yaitu: $k=1+(3,3).\log n$.
- Menentukan panjang kelas ($c$) dengan rumus: $c=\frac{J}{k}$.
- Menyusun daftar distribusi frekuensi dengan menetapkan kelas-kelas sehingga nilai minimum termuat dalam kelas terendah (tidak harus sebagai batas bawah kelas). Selanjutnya menetapkan frekuensi tiap kelas.
Contoh:
Data berikut adalah data jumlah pengunjung perpustakaan SMA NASIONAL dalam 40 hari kerja berturut-turut.

Sajikanlah data tersebut ke dalam tabel distribusi frekuensi data berkelompok.
Penyelesaian:
$x_{maks}=96$ dan $x_{min}=50$
$\begin{align}J &= x_{maks}-x_{min} \\ &= 96-50 \\ J &= 46 \end{align}$
Banyak kelas (k):
$\begin{align}k &= 1+(3,3)\log n \\ &= 1+(3,3).\log 40 \\ &= 1+(3,3)\times (1,6) \\ &= 1+5,28 \\ k &= 6,28 \end{align}$
Ingat dalam menentukan banyak kelas gunakan pembulatan ke atas. Jadi, k = 7.
Panjang kelas (c):
$\begin{align}c &= \frac{J}{k} \\ &= \frac{46}{7} \\ c &= 6,57 \end{align}$
Pembulatan ke atas, maka c = 7
Kemudian kita susun daftar distribusi frekuensi dengan menetapkan interval sehingga nilai minimum 50 termuat dalam kelas terendah dan nilai maksimum 96 termuat dalam kelas tertinggi. Selanjutnya menetapkan frekuensi tiap kelas. Hasilnya seperti tabel di bawah ini.

Atau dapat juga seperti tabel berikut:

D. Tabel Distribusi Frekuensi Kumulatif
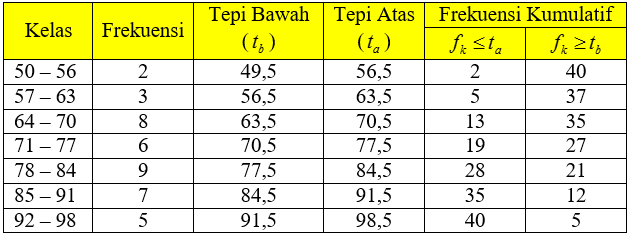
Tabel distribusi frekuensi kumulatif terdiri dari dua jenis yaitu frekuensi kumulatif kurang dari tepi atas ($f_k \le t_a$) dan frekuensi kumulatif lebih dari tepi bawah ($f_k \ge t_b$).Contoh:
Sajikanlah data berikut ini ke dalam tabel distribusi frekuensi kumulatif.

Penyelesaian:

E. Soal Latihan
Berat badan (dalam kg) dari 50 anak adalah sebagai berikut:
Sajikan data di atas dalam tabel distribusi frekuensi data berkelompok, lengkap dengan frekuensi kumulatifnya.

Post a Comment for "Statistika 3. Penyajian Data Dalam Bentuk Tabel Distibusi Frekuensi"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.