Statistika 8. Median Data Tunggal dan Data Berkelompok

A. Definisi Median (Me)

Median adalah suatu nilai yang membagi data menjadi dua bagian yang sama banyaknya setelah data tersebut diurutkan dari yang terkecil hingga yang terbesar.

B. Median Data Tunggal

Misalkan terdapat data $x_1$, $x_2$, $x_3$, ..., $x_n$ dengan $x_1 < x_2 < x_3 < ... < x_n$ maka median (Me) data tersebut adalah:
$Me=x_{\frac{n+1}{2}}$; untuk $n$ ganjil.
$Me=\frac{1}{2}\left( x_{\frac{n}{2}}+x_{\frac{n}{2}+1} \right)$; untuk $n$ genap.

---

Contoh1.
Tentukan median dari data: 2, 4, 3, 3, 7, 2, 6, 12, 8.
Penyelesaian:
Urutkan data dari yang terkecil hingga yang terbesar yaitu:
2, 2, 3, 3, 4, 6, 7, 8, 12
$n=9$ (ganjil)
$\begin{align}Me &= x_{\frac{n+1}{2}} \\ &= x_{\frac{9+1}{2}} \\ &= x_5 \\ &= data\,ke-5 \\ Me &= 4 \end{align}$

---

Contoh 2.
Tentukan median dari data: 4, 8, 7, 3, 6, 7, 9, 8, 2, 1.
Penyelesaian:
Urutkan data dari data yang terkecil hingga yang terbesar, yaitu:
1, 2, 3, 4, 6, 7, 7, 8, 8, 9
$n=10$ (genap)
$\begin{align}Me &= \frac{1}{2}\left( x_{\frac{n}{2}}+x_{\frac{n}{2}+1} \right) \\ &= \frac{1}{2}\left( x_{\frac{10}{2}}+x_{\frac{10}{2}+1} \right) \\ &= \frac{1}{2}\left( x_5+x_6 \right) \\ &= \frac{1}{2}(6+7) \\ Me &= 6,5 \end{align}$

---

C. Median Data Berkelompok

$Me=Tb+\left( \frac{\frac{1}{2}n-fk}{f} \right).c$
Keterangan:
$Me$ = median data
$Tb$ = tepi bawah kelas median
$n$ = banyak data (jumlah frekuensi)
$fk$ = jumlah frekuensi sebelum kelas median.
$f$ = frekuensi kelas median

---

Contoh1.
Tentukan median data pada tabel berikut.

Penyelesaian:
$n$ = 3 + 4 + 5 + 10 + 15 + 6 + 5
$n$ = 48
$\begin{align}Me &= data\,ke-\frac{n}{2} \\ &= data\,ke-\frac{48}{2} \\ Me &= data\,ke-24 \end{align}$
Untuk memudahkan, kita tentukan frekuensi kumulatifnya, seperti tabel berikut.

Data ke-24 terletak pada kelas: 60 – 64 maka:
f = 15 dan fk = 22
Tepi bawah kelas median adalah:
Tb = 60 – ½(60 – 59) = 59,5
Tepi atas kelas median adalah:
Ta = 64 + ½(65 – 64) = 64,5
c = Ta – Tb = 64,5 – 59,5 = 5
Jadi, median data pada tabel tersebut adalah:
$\begin{align}Me &= Tb+\left( \frac{\frac{1}{2}n-fk}{f} \right).c \\ &= 59,5+\left( \frac{\frac{1}{2}.48-22}{15} \right).5 \\ &= 59,5+\frac{10}{15} \\ &= 59,5+0,67 \\ Me &= 60,17 \end{align}$

---

Contoh 2.
Perhatikan histogram data berikut!

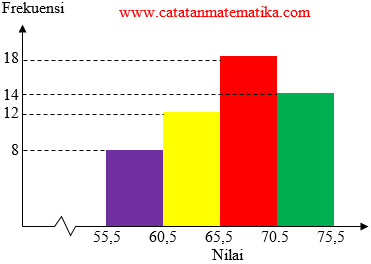
Median dari data pada histogram di atas adalah ...
Penyelesaian:
Berdasarkan histogram kita peroleh:
$n$ = jumlah frekuensi
$n$ = 8 + 12 + 18 + 14 = 52
$\begin{align}Me &= data\,ke-\frac{n}{2} \\ &= data\,ke-\frac{52}{2} \\ Me &= data\,ke-26 \end{align}$
Data ke-26 terletak pada kelas ketiga: 65,5 – 70,5 maka
f = 18 dan fk = 8 + 12 = 20
c = 70,5 – 65,5 = 5
Tepi bawah kelas median adalah:
Tb = 65,5
Tepi atas kelas median adalah:
Ta = 70,5
Jadi, median data pada histogram tersebut adalah:
$\begin{align}Me &= Tb+\left( \frac{\frac{1}{2}n-fk}{f} \right).c \\ &= 65,5+\left( \frac{\frac{1}{2}.52-20}{18} \right).5 \\ &= 65,5+\frac{30}{18} \\ &= 65,5+1,67 \\ Me &= 67,17 \end{align}$

---

Contoh 3.
Median dari data pada ogive positif berikut adalah ...

Penyelesaian:
Berdasarkan ogive positif pada soal.
$n=40$
$\begin{align}Me &= data\,ke-\frac{n}{2} \\ &= data\,ke-\frac{40}{2} \\ Me &= data\,ke-20 \end{align}$
Data ke-20 terletak pada kelas: 11,5 – 16,5 maka:
fk = 15, f = 28 – 15 = 13
Tepi bawah kelas median adalah:
Tb = 11,5
Tepi atas kelas median adalah:
Ta = 16,5
Panjang kelas adalah:
c = Ta – Tb = 16,5 – 11,5 = 5
Jadi, median data pada ogive positif tersebut adalah:
$\begin{align}Me &= Tb+\left( \frac{\frac{1}{2}n-fk}{f} \right).c \\ &= 11,5+\left( \frac{\frac{1}{2}\times 40-15}{13} \right).5 \\ &= 11,5+\frac{25}{13} \\ &= 11,5+1,92 \\ Me &= 13,42 \end{align}$

---

D. Soal Latihan

1.	Median dari data 7, 4, 10, 9, 15, 12, 7, 9, 7 adalah ..
2.	Perhatikan tabel berikut ini. Tentukan median dari data pada tabel tersebut.
3.	Perhatikan data pada tabel nilai hasil ulangan fisika kelas XII IPA.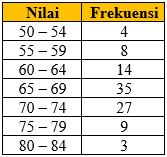 Tentukan median dari data tersebut.
4.	Perhatikan data yang disajikan pada histogram berikut. Tentukan median dari data tersebut!
5.	Data berikut adalah tinggi badan sekelompok siswa. Diketahui median data di atas adalah 163,5 cm. Tentukan nilai $k$.

Share :