Pembahasan Soal SMA Taruna Nusantara Seleksi Akademik Tahun 2018 - Latihan Soal 2025
Selamat datang di Website Catatan Matematika, website belajar matematika secara online dan mandiri. Berikut ini Catatan Matematika berbagi Pembahasan Soal Matematika Seleksi Masuk SMA Taruna Nusantara Tahun 2018 Bidang Studi Matematika. Pembahasan Soal Seleksi SMA Taruna Nusantara ini dapat dijadikan sebagai bahan belajar bagi adik-adik yang ingin menjadi salah satu siswa di SMA Taruna Nusantara Magelang secara khusus dan SMA Favorit dan SMA Unggulan lainnya secara umum.
A. –30
B. –15
C. 15
D. 30
Jawaban: D
Video Pembahasan:
i ) {(1, a), (2, a), (3, a), (4, a)}
ii) {(2, b), (3, c), (4, d), (2, e)}
iii) {(3, 6), (4, 6), (5, 10), (3, 12)}
iv) {(1, 5), (3, 7), (5, 9), (3, 11)}
Relasi yang merupakan pemetaan adalah ...
A. i
B. ii
C. iii
D. iv
TIPS:
Syarat pemetaan pada himpunan pasangan terurut, anggota domain berbeda semua.
Yang memenuhi adalah i)
Jawaban: A
Video Pembahasan:
A.
B.
C.
D.
HP =
Jawaban: D
Video Pembahasan:
A. x + 2y = 94.000 dan 3x + 2y = 167.000
B. 2x + y = 94.000 dan 3x + 2y = 167.000
C. 2x + y = 94.000 dan 2x + 3y = 167.000
D. x + 2y = 94.000 dan 2x + 3y = 167.000
y = harga 1 kg anggur
Andre membeli 1 kg pear dan 2 kg anggur dengan harga Rp. 94.000,-
Ditulis: x + 2y = 94.000
Setiawan membeli 3 kg anggur dan 2 kg pear dengan harga Rp. 167.000,-
Ditulis: 3y + 2x = 167.000 atau 2x + 3y = 167.000
Jawaban: D
Video Pembahasan:
A. –11
B. –13
C. –15
D. –17
Misal:
Maka:
Jawaban: C
Video Pembahasan:
A. 6
B. 7
C. 8
D. 9
Dengan melihat koefisien
Nilai
Jawaban: C
Video Pembahasan:
A. Sama kaki
B. Siku-siku
C. Lancip
D. Tumpul
Sementara pada soal sisi terpanjangnya 19 cm < 20 cm, maka segitiga tersebut adalah segitiga lancip.
Jawaban: C
Video Pembahasan:

A. 30
B. 48
C. 60
D. 78
ii)
iii)
dari i), ii) dan iii) diperoleh:
Teorema pythagoras:
Luas segitiga adalah:
Jawaban: A
Video Pembahasan:

A.
B.
C.
D.
Jawaban: C
Video Pembahasan:
A. 9
B. 10
C. 12
D. 15
Banyak rusuk prisma segi-5 adalah 3.5 = 15.
Jawaban: D
Video Pembahasan:

Diketahui keliling lingkaran 314 cm, besar
A. 1.470
B. 1.570
C. 2.570
D. 7.850
Jadi, luas juring POQ adalah 1.570
Jawaban: B
Video Pembahasan:
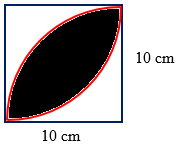
A. 57,0
B. 34,0
C. 27,5
D. 22,5
Jawaban: A
Video Pembahasan:

A. 6.750
B. 4.500
C. 3.250
D. 2.250
Volume balok ABCD.EFGH yang berada di luar limas adalah:
=
= 6.750 – 2.250
= 4.500
Jawaban: B
Video Pembahasan:
A. 20 cm
B. 14 cm
C. 10 cm
D. 7 cm

R = jari-jari bola
r = jari-jari kerucut
maka:
Jawaban: D
Video Pembahasan:
13 siswa mengikuti atletik
13 siswa mengikuti sepak takraw
11 siswa mengikuti basket
3 siswa mengikuti atletik dan sepak takraw
3 siswa mengikuti atletik dan basket
4 siswa mengikuti sepak takraw dan basket
3 siswa tidak mengikuti ketiga kegiatan ekstrakulikuler olahraga
Banyaknya siswa dalam 1 kelas tersebut adalah ...
A. 29
B. 30
C. 31
D. 32

Dari diagram venn diperoleh banyak siswa 1 kelas adalah:
= 9 + 1 + 2 + 1 + 3 + 8 + 2 + 6
= 32
Jawaban: D
Video Pembahasan:
A. 9
B. 18
C. 20
D. 25
Banyak susunan pemain yang mungkin adalah:
= banyak cara memilih 1 putra dari 4 putra dan banyak cara memilih 1 putri dari 5 putri
= 4 x 5
= 20
Jawaban: C
Video Pembahasan:
A. 12 titik sampel
B. 18 titik sampel
C. 20 titik sampel
D. 24 titik sampel
Banyak anggota ruang sampel pada pelemparan sebuah dadu adalah 6 titik sampel.
Jadi, banyak ruang sampel pada pelemparan sekeping uang logam dan sebuah dadu secara bersamaan adalah 2 x 6 = 12 titik sampel.
Jawaban: A
Video Pembahasan:
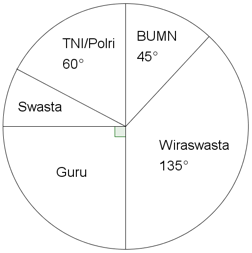
A. 30
B. 45
C. 50
D. 60
=
=
Banyak orang tua yang berprofesi swasta adalah:
=
= 45 orang.
Jawaban: B
Video Pembahasan:
A. 81
B. 82
C. 84
D. 85
Jawaban: A
Video Pembahasan:

A. 6 siswa
B. 9 siswa
C. 11 siswa
D. 15 siswa
Siswa dinyatakan lulus ujian jika nilainya lebih dari rata-rata nilai seluruh peserta ujian. Jadi, siswa yang lulus adalah siswa yang nilainya 8, 9, dan 10.
Banyak siswa yang lulus adalah:
= 4 + 4 + 1
= 9 orang
Jawaban: B
Video Pembahasan:
A. 8
B. 4
C. 2
D. 1
Jawaban: D
Video Pembahasan:
A.
B.
C.
D.
Untuk
1)
2)
=
=
=
=
=
=
Jawaban: A
Video Pembahasan:
A. 1150 orang
B. 1100 orang
C. 1050 orang
D. 1000 orang
Jumlah penonton yang hadir di dalam gedung adalah:
Jawaban: A
Video Pembahasan:
A.
B. 7%;
C. 0,5;
D. 7%; 0,5;
7% = 0,07
Jadi, urutan dari kecil ke besar adalah:
0,07; 0,375; 0,5; 0,85
7%;
Jawaban: B
Video Pembahasan:
A.
B.
C.
D.
Jawaban: C
Video Pembahasan:
A. 87
B. 83
C. 80
D. 79
Soal benar (B) = 27
Soal salah (S) = 8
Tidak dijawab (K)= 40 – 27 – 8 = 5
Jadi, nilai yang diperoleh siswa adalah:
= 4xB + (-3)xS + (-1)xK
= 4x27 – 3x8 – 1x5
= 108 – 24 – 5
= 79
Jawaban: D
Video Pembahasan:
A.
B.
C.
D.
Jawaban: D
Video Pembahasan:
A. Rp. 1.200.000,00
B. Rp. 1.360.000,00
C. Rp. 1.420.000,00
D. Rp. 1.480.000,00
Tidak kena pajak = Rp. 400.000,00
Yang kena pajak = Rp. 1.600.000,00 – Rp. 400.000,00
Yang kena pajak = Rp. 1.200.000,00
Pajak penghasila 15% maka gaji yang diterima adalah:
= (100 – 15)% x 1.200.000 + 400.000
= 1.020.000 + 400.000
= 1.420.000
Jawaban: C
Video Pembahasan:
I.
II.
III.
IV.
Pernyataan yang benar adalah ...
A. I dan III
B. II dan IV
C. I, II dan III
D. IV saja
Pernyataan II:
Pernyataan III:
Pernyataan IV:
Jadi, pernyataan yang benar adalah II dan IV.
Jawaban: B
Video Pembahasan:
A. –2
B. –1
C. 1
D. 2
-------------------------------- (-)
Nilai
Jawaban: A
Video Pembahasan:
By: Catatan Matematika
Tata Cara Belajar:
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cocokkanlah jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik Lihat/Tutup atau klik untuk menonton video pembahasan.
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cocokkanlah jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik Lihat/Tutup atau klik untuk menonton video pembahasan.
Seleksi SMA Taruna Nusantara 2018 No. 1
Diketahui fungsi A. –30
B. –15
C. 15
D. 30
Penyelesaian: Lihat/Tutup
Jawaban: D
Seleksi SMA Taruna Nusantara 2018 No. 2
Perhatikan relasi berikut:i ) {(1, a), (2, a), (3, a), (4, a)}
ii) {(2, b), (3, c), (4, d), (2, e)}
iii) {(3, 6), (4, 6), (5, 10), (3, 12)}
iv) {(1, 5), (3, 7), (5, 9), (3, 11)}
Relasi yang merupakan pemetaan adalah ...
A. i
B. ii
C. iii
D. iv
Penyelesaian: Lihat/Tutup
Perhatikan bahwa pada (x,y) maka x = domain, dan y = range.TIPS:
Syarat pemetaan pada himpunan pasangan terurut, anggota domain berbeda semua.
Yang memenuhi adalah i)
Jawaban: A
Seleksi SMA Taruna Nusantara 2018 No. 3
Himpunan penyelesaian dari A.
B.
C.
D.
Penyelesaian: Lihat/Tutup
HP =
Jawaban: D
Seleksi SMA Taruna Nusantara 2018 No. 4
Andre membeli 1 kg pear dan 2 kg anggur dengan harga Rp. 94.000,-. Setiawan membeli 3 kg anggur dan 2 kg pear dengan harga Rp. 167.000,-. Jika harga 1 kg pear dinyatakan dengan x dan harga 1 kg anggur dinyatakan dengan y, sistem persamaan linear dua variabel yang berkaitan dengan pernyataan di atas adalah ...A. x + 2y = 94.000 dan 3x + 2y = 167.000
B. 2x + y = 94.000 dan 3x + 2y = 167.000
C. 2x + y = 94.000 dan 2x + 3y = 167.000
D. x + 2y = 94.000 dan 2x + 3y = 167.000
Penyelesaian: Lihat/Tutup
x = harga 1 kg peary = harga 1 kg anggur
Andre membeli 1 kg pear dan 2 kg anggur dengan harga Rp. 94.000,-
Ditulis: x + 2y = 94.000
Setiawan membeli 3 kg anggur dan 2 kg pear dengan harga Rp. 167.000,-
Ditulis: 3y + 2x = 167.000 atau 2x + 3y = 167.000
Jawaban: D
Seleksi SMA Taruna Nusantara 2018 No. 5
Diketahui A. –11
B. –13
C. –15
D. –17
Penyelesaian: Lihat/Tutup
Misal:
Maka:
Jawaban: C
Seleksi SMA Taruna Nusantara 2018 No. 6
Diketahui A. 6
B. 7
C. 8
D. 9
Penyelesaian: Lihat/Tutup
Dengan melihat koefisien
Nilai
Jawaban: C
Seleksi SMA Taruna Nusantara 2018 No. 7
Sebuah segitiga memiliki panjang sisi 12 cm, 16 cm, dan 19 cm. Segitiga tersebut merupakan jenis segitiga ...A. Sama kaki
B. Siku-siku
C. Lancip
D. Tumpul
Penyelesaian: Lihat/Tutup
Perhatikan dua sisi terpendek: 12 cm dan 16 cm. Jika segitiga tersebut segitiga siku-siku maka panjang sisi terpanjangnya harus memenuhi teorema pythagoras, yaitu:Sementara pada soal sisi terpanjangnya 19 cm < 20 cm, maka segitiga tersebut adalah segitiga lancip.
Jawaban: C
Seleksi SMA Taruna Nusantara 2018 No. 8
Gambar di bawah ini menunjukkan segitiga siku-siku dengan panjang sisi 
A. 30
B. 48
C. 60
D. 78
Penyelesaian: Lihat/Tutup
i)ii)
iii)
dari i), ii) dan iii) diperoleh:
Teorema pythagoras:
Luas segitiga adalah:
Jawaban: A
Seleksi SMA Taruna Nusantara 2018 No. 9
Besar 
A.
B.
C.
D.
Penyelesaian: Lihat/Tutup
Jawaban: C
Seleksi SMA Taruna Nusantara 2018 No. 10
Banyaknya rusuk suatu prisma tegak yang alasnya segilima beraturan adalah ... buahA. 9
B. 10
C. 12
D. 15
Penyelesaian: Lihat/Tutup
Banyak rusuk prisma segi-n adalah 3n.Banyak rusuk prisma segi-5 adalah 3.5 = 15.
Jawaban: D
Seleksi SMA Taruna Nusantara 2018 No. 11
Perhatikan gambar!
Diketahui keliling lingkaran 314 cm, besar
A. 1.470
B. 1.570
C. 2.570
D. 7.850
Penyelesaian: Lihat/Tutup
Jadi, luas juring POQ adalah 1.570
Jawaban: B
Seleksi SMA Taruna Nusantara 2018 No. 12
Luas daerah yang diarsir pada gambar di bawah ini (
A. 57,0
B. 34,0
C. 27,5
D. 22,5
Penyelesaian: Lihat/Tutup
Luar arsir = 2 kali luas tembereng lingkaran.Jawaban: A
Seleksi SMA Taruna Nusantara 2018 No. 13
Pada gambar di bawah ini, bidang alas balok berukuran AB = 30 cm, BC = 15 cm, dan volume limas H.ABCD = 2.250 
A. 6.750
B. 4.500
C. 3.250
D. 2.250
Penyelesaian: Lihat/Tutup
Volume balok ABCD.EFGH yang berada di luar limas adalah:
=
= 6.750 – 2.250
= 4.500
Jawaban: B
Seleksi SMA Taruna Nusantara 2018 No. 14
Alas sebuah kerucut pejal berhimpit dengan alas setengah bola pejal. Tinggi kerucut 12 cm. Diameter setengah bola tersebut adalah 30 cm. Jika jumlah volume keduanya 7.681 A. 20 cm
B. 14 cm
C. 10 cm
D. 7 cm
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
R = jari-jari bola
r = jari-jari kerucut
maka:
Jawaban: D
Seleksi SMA Taruna Nusantara 2018 No. 15
Dalam suatu kelas dilakukan pendataan tentang kegiatan ekstrakurikuler olahraga yang diikuti oleh siswa di kelas tersebut. Didapatkan data sebagai berikut:13 siswa mengikuti atletik
13 siswa mengikuti sepak takraw
11 siswa mengikuti basket
3 siswa mengikuti atletik dan sepak takraw
3 siswa mengikuti atletik dan basket
4 siswa mengikuti sepak takraw dan basket
2 siswa mengikuti ketiga kegiatan ekstrakulikuler olahraga
3 siswa tidak mengikuti ketiga kegiatan ekstrakulikuler olahraga
Banyaknya siswa dalam 1 kelas tersebut adalah ...
A. 29
B. 30
C. 31
D. 32
Penyelesaian: Lihat/Tutup
Data kita sajikan ke dalam diagram venn, sebagai berikut:
Dari diagram venn diperoleh banyak siswa 1 kelas adalah:
= 9 + 1 + 2 + 1 + 3 + 8 + 2 + 6
= 32
Jawaban: D
Seleksi SMA Taruna Nusantara 2018 No. 16
Suatu klub bulu tangkis memiliki 4 pemain putra dan 5 pemain putri. Jika akan dibentuk 1 regu campuran untuk pertandingan bulu tangkis maka banyaknya susunan pemain yang mungkin adalah ...A. 9
B. 18
C. 20
D. 25
Penyelesaian: Lihat/Tutup
Untuk membentuk 1 regu ganda campuran dibutuhkan 1 putra dan 1 putri.Banyak susunan pemain yang mungkin adalah:
= banyak cara memilih 1 putra dari 4 putra dan banyak cara memilih 1 putri dari 5 putri
= 4 x 5
= 20
Jawaban: C
Seleksi SMA Taruna Nusantara 2018 No. 17
Banyak anggota ruang sampel pada pelemparan sekeping uang logam dan sebuah dadu yang dilakukan secara bersamaan adalah ...A. 12 titik sampel
B. 18 titik sampel
C. 20 titik sampel
D. 24 titik sampel
Penyelesaian: Lihat/Tutup
Banyak anggota ruang sampel pada pelemparan sekeping uang logam adalah 2 titik sampel.Banyak anggota ruang sampel pada pelemparan sebuah dadu adalah 6 titik sampel.
Jadi, banyak ruang sampel pada pelemparan sekeping uang logam dan sebuah dadu secara bersamaan adalah 2 x 6 = 12 titik sampel.
Jawaban: A
Seleksi SMA Taruna Nusantara 2018 No. 18
Data 540 siswa SMA Taruna Nusantara diketahui bahwa pekerjaan orang tua para siswa tersebut tergambar dalam diagram di bawah ini. Banyak orang tua siswa yang berprofesi swasta adalah ...
A. 30
B. 45
C. 50
D. 60
Penyelesaian: Lihat/Tutup
Besar sudut diagram swasta adalah:=
=
Banyak orang tua yang berprofesi swasta adalah:
=
= 45 orang.
Jawaban: B
Seleksi SMA Taruna Nusantara 2018 No. 19
Alisha mendapatkan nilai rata-rata dari tiga ulangan matematika yang diikutinya adalah 81. Nilai ulangan yang pertama 85. Nilai ulangan ketiga lebih rendah 4 dari nilai ulangan kedua. Nilai ulangan Alisha yang kedua adalah ...A. 81
B. 82
C. 84
D. 85
Penyelesaian: Lihat/Tutup
Jawaban: A
Seleksi SMA Taruna Nusantara 2018 No. 20
Siswa dinyatakan lulus ujian jika nilainya lebih dari rata-rata nilai seluruh peserta ujian. Diagram di bawah ini, menunjukkan nilai dari seluruh peserta. Banyak siswa yang tidak lulus adalah ...
A. 6 siswa
B. 9 siswa
C. 11 siswa
D. 15 siswa
Penyelesaian: Lihat/Tutup
Siswa dinyatakan lulus ujian jika nilainya lebih dari rata-rata nilai seluruh peserta ujian. Jadi, siswa yang lulus adalah siswa yang nilainya 8, 9, dan 10.
Banyak siswa yang lulus adalah:
= 4 + 4 + 1
= 9 orang
Jawaban: B
Seleksi SMA Taruna Nusantara 2018 No. 21
Hasil dari A. 8
B. 4
C. 2
D. 1
Penyelesaian: Lihat/Tutup
Jawaban: D
Seleksi SMA Taruna Nusantara 2018 No. 22
Bentuk rasional dari A.
B.
C.
D.
Penyelesaian: Lihat/Tutup
Ingat:Untuk
1)
2)
=
=
=
=
=
=
Jawaban: A
Seleksi SMA Taruna Nusantara 2018 No. 23
Sebuah Gedung pertunjukan terdiri atas 20 baris kursi penonton yang disusun dari depan ke belakang dengan pertambahan kursi yang sama. Pada baris yang pertama (terdepan) tersusun 10 kursi, sedangkan pada baris kelima tersusun 30 kursi. Pada malam tersebut, jumlah penonton yang hadir di dalam Gedung itu adalah ...A. 1150 orang
B. 1100 orang
C. 1050 orang
D. 1000 orang
Penyelesaian: Lihat/Tutup
Permasalahan di atas berkaitan dengan Deret Aritmetika.Jumlah penonton yang hadir di dalam gedung adalah:
Jawaban: A
Seleksi SMA Taruna Nusantara 2018 No. 24
Urutan A.
B. 7%;
C. 0,5;
D. 7%; 0,5;
Penyelesaian: Lihat/Tutup
7% = 0,07
Jadi, urutan dari kecil ke besar adalah:
0,07; 0,375; 0,5; 0,85
7%;
Jawaban: B
Seleksi SMA Taruna Nusantara 2018 No. 25
Nilai dari A.
B.
C.
D.
Penyelesaian: Lihat/Tutup
Jawaban: C
Seleksi SMA Taruna Nusantara 2018 No. 26
Seorang siswa mengerjakan 40 soal, 27 soal benar, 8 soal salah dan sisanya tidak dikerjakan. Jika satu soal dijawab benar nilainya 4, salah nilainya –3, serta tidak menjawab nilainya – 1, maka nilai yang diperoleh siswa tersebut adalah ...A. 87
B. 83
C. 80
D. 79
Penyelesaian: Lihat/Tutup
Jumlah soal = 40Soal benar (B) = 27
Soal salah (S) = 8
Tidak dijawab (K)= 40 – 27 – 8 = 5
Jadi, nilai yang diperoleh siswa adalah:
= 4xB + (-3)xS + (-1)xK
= 4x27 – 3x8 – 1x5
= 108 – 24 – 5
= 79
Jawaban: D
Seleksi SMA Taruna Nusantara 2018 No. 27
Diketahui suku ke-3 suatu barisan geometri adalah A.
B.
C.
D.
Penyelesaian: Lihat/Tutup
Barisan Geometri:Jawaban: D
Seleksi SMA Taruna Nusantara 2018 No. 28
Seorang pegawai toko mendapat gaji per bulan sebesar Rp. 1.600.000,00 dengan penghasilan tidak kena pajak sebesar Rp. 400.000,00. Jika besar pajak penghasilan 15%, besar gaji yang diterima adalah ...A. Rp. 1.200.000,00
B. Rp. 1.360.000,00
C. Rp. 1.420.000,00
D. Rp. 1.480.000,00
Penyelesaian: Lihat/Tutup
Gaji = Rp. 1.600.000,00Tidak kena pajak = Rp. 400.000,00
Yang kena pajak = Rp. 1.600.000,00 – Rp. 400.000,00
Yang kena pajak = Rp. 1.200.000,00
Pajak penghasila 15% maka gaji yang diterima adalah:
= (100 – 15)% x 1.200.000 + 400.000
= 1.020.000 + 400.000
= 1.420.000
Jawaban: C
Seleksi SMA Taruna Nusantara 2018 No. 29
Perhatikan pemfaktoran berikut:I.
II.
III.
IV.
Pernyataan yang benar adalah ...
A. I dan III
B. II dan IV
C. I, II dan III
D. IV saja
Penyelesaian: Lihat/Tutup
Pernyataan I:Pernyataan II:
Pernyataan III:
Pernyataan IV:
Jadi, pernyataan yang benar adalah II dan IV.
Jawaban: B
Seleksi SMA Taruna Nusantara 2018 No. 30
Penyelesaian dari A. –2
B. –1
C. 1
D. 2
Penyelesaian: Lihat/Tutup
-------------------------------- (-)
Nilai
Jawaban: A
By: Catatan Matematika









Sangat bermanfaat untuk persiapan anak-anak..
ReplyDelete