Home / Lingkaran

Lingkaran 4. Kedudukan Titik Terhadap Lingkaran

Post a Comment

A. Kedudukan Titik Terhadap Lingkaran

Perhatikan gambar berikut!
Kedudukan Titik Terhadap Lingkaran
Berdasarkan gambar kedudukan titik terhadap lingkaran terbagi menjadi tiga kondisi yaitu:
  1. Titik A terletak di dalam lingkaran.
  2. Titik B terletak pada lingkaran.
  3. Titik C terletak di luar lingkaran.

B. Kedudukan Titik $(x_1,y_1)$ terhadap Lingkaran $x^2+y^2=r^2$

Cara menentukan kedudukan titik $(x_1,y_1)$ terhadap lingkaran $x^2+y^2=r^2$ yaitu dengan substitusi koordinat titik $(x_1,y_1)$ ke persamaan lingkaran $x^2+y^2=r^2$ akan diperoleh tiga kemungkinan, yaitu:
  1. Jika $x_1^2+y_1^2 < r^2$ maka titik $(x_1,y_1)$ terletak di dalam lingkaran.
  2. Jika $x_1^2+y_1^2 = r^2$ maka titik $(x_1,y_1)$ terletak pada lingkaran.
  3. Jika $x_1^2+y_1^2 > r^2$ maka titik $(x_1,y_1)$ terletak di luar lingkaran.
Contoh 1.
Tanpa melukis lingkaran $x^2+y^2=169$, tentukanlah posisi titik $P(-1,13)$, $Q(5,12)$ dan $R(-1,10)$ terhadap lingkaran.
Penyelesaian:
Untuk menentukan kedudukan titik (x,y) terhadap lingkaran $x^2+y^2=169$, kita substitusi nilai x dan y ke persamaan lingkaran, tanda “=” kita kosongkan terlebih dahulu. Kemudian pada hasil akhir kita berikan salah satu tanda berikut: “<”, “=”, atau “>” sesuai kondisi yang sebenarnya.
$P(-1,13)\Rightarrow x=-1,\,y=13$, maka:
$\begin{array}{*{35}{r}}x^2+y^2 & ... & 169 \\(-1)^2+13^2 & ... & 169 \\ 1+169 & ... & 169 \\ 170 & > & 169 \\ \end{array}$
Jadi, titik $P(-1,13)$ terletak di luar lingkaran.

$Q(5,12)\Rightarrow x=5,\,y=12$
$\begin{array}{*{35}{r}}x^2+y^2 & ... & 169 \\5^2+12^2 & ... & 169 \\ 25+144 & ... & 169 \\ 169 & = & 169 \\ \end{array}$
Jadi, titik $Q(5,12)$ terletak pada lingkaran.

$R(-1,10)\Rightarrow x=-1,\,y=10$
$\begin{array}{*{35}{r}}x^2+y^2 & ... & 169 \\ (-1)^2+10^2 & ... & 169 \\ 1+100 & ... & 169 \\ 101 & < & 169 \\ \end{array}$
Jadi, titik $R(-1,10)$ terletak di dalam lingkaran.
Contoh 2.
Tentukan nilai $a$ agar titik $Q(-4,a)$ terletak di dalam lingkaran $x^2+y^2=20$.
Penyelesaian:
Titik $Q(-4,a)\Rightarrow x=-4,\,y=a$ terletak di dalam lingkaran $x^2+y^2=20$ maka:
$\begin{align}x^2+y^2 & < 20 \\ (-4)^2+a^2 & < 20 \\ 16+a^2 & < 20 \\ a^2-4 & < 0 \\ (a+2)(a-2) & < 0 \end{align}$
Pembuat nol: $a=-2$ atau $a=2$
Garis bilangan:
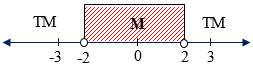
Tentukan Nilai a agar Q(-4,a) terletak di dalam lingkaran
$-2 < a < 2$
Jadi, agar titik $Q(-4,a)$ terletak di dalam lingkaran $x^2+y^2=20$ maka batas-batas nilai $a$ adalah $-2 < a < 2$.
Contoh 3.
Tentukan nilai $k$ agar titik $A(2,k)$ terletak pada lingkaran $x^2+y^2=13$.
Penyelesaian:
Titik $A(2,k)\Rightarrow x=2,\,y=k$ terletak pada lingkaran $x^2+y^2=13$ maka:
$\begin{align}x^2+y^2 &= 13 \\ 2^2+k^2 &= 13 \\ 4+k^2 &= 13 \\ k^2-9 &= 0 \\ (k+3)(k-3) &= 0 \end{align}$
$k=-3$ atau $k=3$
Contoh 4.
Tentukan nilai $m$ agar titik $P(\sqrt{m},m)$ terletak di luar lingkaran $x^2+y^2=6$.
Penyelesaian:
Titik $P(\sqrt{m},m)\Rightarrow x=\sqrt{m},\,y=m$ terletak di luar lingkaran $x^2+y^2=6$ maka:
$\begin{align}x^2+y^2 &> 6 \\ \left( \sqrt{m} \right)^2+m^2 &> 6 \\ m+m^2 &> 6 \\ m^2+m-6 &> 0 \\ (m+3)(m-2) &> 0 \end{align}$
Pembuat nol: $m=-3$ atau $m=2$
Garis bilangan:
Syarat Titik Terletak di Luar Lingkaran
$m < -3$ atau $m >2$
Jadi, agar titik $P(\sqrt{m},m)$ terletak di luar lingkaran $x^2+y^2=6$ maka batas-batas nilai $m$ adalah $m < -3$ atau $m > 2$.

C. Kedudukan Titik $(x_1,y_1)$ terhadap Lingkaran $(x-a)^2+(y-b)^2=r^2$

Cara menentukan kedudukan titik $(x_1,y_1)$ terhadap lingkaran $(x-a)^2+(y-b)^2=r^2$ yaitu dengan substitusi koordinat titik $(x_1,y_1)$ ke persamaan lingkaran $(x-a)^2+(y-b)^2=r^2$ akan diperoleh tiga kemungkinan, yaitu:
  1. Jika $(x_1-a)^2+(y_1-b)^2 < r^2$ maka titik $(x_1,y_1)$ terletak di dalam lingkaran.
  2. Jika $(x_1-a)^2+(y_1-b)^2=r^2$ maka titik $(x_1,y_1)$ terletak pada lingkaran.
  3. Jika $(x_1-a)^2+(y_1-b)^2 > r^2$ maka titik $(x_1,y_1)$ terletak di luar lingkaran.
Contoh 1.
Tentukan kedudukan titik $A(1,1)$, $B(5,-2)$ dan $C(3,-6)$ terhadap lingkaran $(x-1)^2+(y+2)^2=16$.
Penyelesaian:
Untuk menentukan kedudukan titik (x,y) terhadap lingkaran $(x-1)^2+(y+2)^2=16$, kita substitusi nilai x dan y ke persamaan lingkaran, tanda “=” kita kosongkan terlebih dahulu. Kemudian pada hasil akhir kita berikan salah satu tanda berikut: “<”, “=”, atau “>” sesuai kondisi yang sebenarnya.
$A(1,1)\Rightarrow x=1,y=1$, maka:
$\begin{array}{*{35}{r}}(x-1)^2+(y+2)^2 & ... & 16 \\ (1-1)^2+(1+2)^2 & ... & 16 \\ 0+9 & ... & 16 \\ 9 & < & 16 \\ \end{array}$
Jadi, titik $A(1,1)$ terletak di dalam lingkaran.

$B(5,-2)\Rightarrow x=5,y=-2$, maka:
$\begin{array}{*{35}{r}}(x-1)^2+(y+2)^2 & ... & 16 \\ (5-1)^2+(-2+2)^2 & ... & 16 \\ 16+0 & ... & 16 \\ 16 & = & 16 \\ \end{array}$
Jadi, titik $B(5,-2)$ terletak pada lingkaran.

$C(3,-6)\Rightarrow x=3,y=-6$, maka:
$\begin{array}{*{35}{r}}(x-1)^2+(y+2)^2 & ... & 16 \\ (3-1)^2+(-6+2)^2 & ... & 16 \\ 4+16 & ... & 16 \\ 20 & > & 16 \\ \end{array}$
Jadi, titik $C(3,-6)$ terletak di luar lingkaran.
Contoh 2.
Tentukan nilai $p$ agar titik $A(-4,p)$ terletak pada lingkaran $(x+1)^2+(y-2)^2=25$.
Penyelesaian:
Titik $A(-4,p)\Rightarrow x=-4,y=p$ terletak pada lingkaran $(x+1)^2+(y-2)^2=25$ maka:
$\begin{align}(x+1)^2+(y-2)^2 &= 25 \\ (-4+1)^2+(p-2)^2 &= 25 \\ 9+p^2-4p+4 &= 25 \\ p^2-4p-12 &= 0 \\ (p+2)(p-6) &= 0 \end{align}$
$p+2=0\Rightarrow p=-2$
$p-6=0\Rightarrow p=6$
Jadi, nilai $p=-2$ atau $p=6$.
Contoh 3.
Tentukan nilai $m$ agar titik $B(m,2)$ terletak di luar lingkaran $(x+3)^2+(y-4)^2=20$.
Penyelesaian:
Titik $B(m,2)\Rightarrow x=m,y=2$ terletak di luar lingkaran $(x+3)^2+(y-4)^2=20$ maka:
$\begin{align}(x+3)^2+(y-4)^2 &> 20 \\ (m+3)^2+(2-4)^2 &> 20 \\ m^2+6m+9+4 &> 20 \\ m^2+6m-7 &> 0 \\ (m+7)(m-1) &> 0 \end{align}$
Pembuat nol: $m=-7$ atau $m=1$
Garis bilangan:
Nilai m agar titik B(m,2) terletak di luar lingkaran
$m < -7$ atau $m > 1$
Jadi, agar titik $B(m,2)$ terletak di luar lingkaran $(x+3)^2+(y-4)^2=20$ maka batas-batas nilai $m$ adalah $m < -7$ atau $m > 1$.
Contoh 4.
Diketahui titik $(6,k)$ terletak di dalam lingkaran $(x-2)^2+(y-5)^2=25$. Nilai $k$ yang memenuhi adalah ...
Penyelesaian:
Titik $(6,k)\Rightarrow x=6,y=k$ terletak di dalam lingkaran $(x-2)^2+(y-5)^2=25$ maka:
$\begin{align}(x-2)^2+(y-5)^2 & < 25 \\ (6-2)^2+(k-5)^2 & < 25 \\ 16+k^2-10k+25 & < 25 \\ k^2-10k+16 & < 0 \\ (k-2)(k-8) & < 0 \end{align}$
Pembuat nol: $k=2$ atau $k=8$
Garis bilangan:
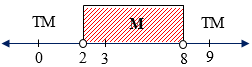
Titik (6,k) terletak di dalam lingkaran
$2 < k < 8$
Jadi, agar titik $(6,k)$ terletak di dalam lingkaran $(x-2)^2+(y-5)^2=25$ maka batas-batas nilai $k$ adalah $2 < k < 8$.

D. Kedudukan Titik $(x_1,y_1)$ terhadap Lingkaran $x^2+y^2+Ax+By+C=0$

Cara menentukan kedudukan titik $(x_1,y_1)$ terhadap lingkaran $x^2+y^2+Ax+By+C=0$ yaitu dengan substitusi koordinat titik $(x_1,y_1)$ ke persamaan lingkaran $x^2+y^2+Ax+By+C=0$, akan diperoleh tiga kemungkinan, yaitu:
  1. Jika $x_1^2+y_1^2+Ax_1+By_1+C < 0$ maka titik $(x_1,y_1)$ terletak di dalam lingkaran.
  2. Jika $x_1^2+y_1^2+Ax_1+By_1+C = 0$ maka titik $(x_1,y_1)$ terletak pada lingkaran.
  3. Jika $x_1^2+y_1^2+Ax_1+By_1+C > 0$ maka titik $(x_1,y_1)$ terletak di luar lingkaran.
Contoh 1.
Tentukan kedudukan titik $K(2,1)$ dan $L(4,-2)$ terhadap lingkaran $x^2+y^2-2x-4y-14=0$.
Penyelesaian:
Untuk menentukan kedudukan titik (x,y) terhadap lingkaran $x^2+y^2-2x-4y-14=0$, kita substitusi nilai x dan y ke persamaan lingkaran, tanda “=” kita kosongkan terlebih dahulu. Kemudian pada hasil akhir kita berikan salah satu tanda berikut: “<”, “=”, atau “>” sesuai kondisi yang sebenarnya.

Titik $K(2,1)\Rightarrow x=2,y=1$ maka:
$\begin{array}{*{35}{r}}x^2+y^2-2x-4y-14 & ... & 0 \\ 2^2+1^2-2.2-4.1-14 & ... & 0 \\ 4+1-4-4-14 & ... & 0 \\ -17 & < & 0 \\ \end{array}$
Jadi, titik $K(2,1)$ terletak di dalam lingkaran.

Titik $L(4,-2)\Rightarrow x=4,y=-2$ maka:
$\begin{array}{*{35}{r}} x^2+ y^2-2x-4y-14 & ... & 0 \\ 4^2+(-2)^2-2.4-4.(-2)-14 & ... & 0 \\ 16+4-8+8-14 & ... & 0 \\ 6 & > & 0 \\ \end{array}$
Jadi, titik $K(2,1)$ terletak di luar lingkaran.
Contoh 2.
Titik $(3,1)$ terletak pada lingkaran $2{{x}^{2}}+2{{y}^{2}}+px+8y+8=0$. Tentukan nilai $p$.
Penyelesaian:
Titik $(3,1)\Rightarrow x=3,y=1$ terletak pada lingkaran $2x^2+2y^2+px+8y+8=0$ maka:
$\begin{align}2x^2+2y^2+px+8y+8 &= 0 \\ 2.3^2+2.1^2+p.3+8.1+8 &= 0 \\ 18+2+3p+8+8 &= 0 \\ 3p+36 &= 0 \\ 3p &= -36 \\ p &= -12 \end{align}$
Jadi, nilai $p=-12$.
Contoh 3.
Jika titik $(-5,k)$ terletak di luar lingkaran $x^2+y^2+2x-5y-21=0$, tentukan nilai $k$.
Penyelesaian:
Titik $(-5,k)\Rightarrow x=-5,y=k$ terletak di luar lingkaran ${{x}^{2}}+{{y}^{2}}+2x-5y-21=0$, maka:
$\begin{align}x^2+y^2+2x-5y-21 &> 0 \\ (-5)^2+k^2+2(-5)-5.k-21 &> 0 \\ 25+k^2-10-5k-21 &> 0 \\ k^2-5k-6 &> 0 \\ (k+1)(k-6) &> 0 \end{align}$
Pembuat nol: $k=-1$ atau $k=6$
Garis bilangan:
titik (-5,k) terletak di luar lingkaran
$k < -1$ atau $k > 6$
Jadi, agar titik $(-5,k)$ terletak di luar lingkaran $x^2+y^2+2x-5y-21=0$ maka batas-batas nilai $k$ adalah $k < -1$ atau $k > 6$.
Contoh 4.
Titik $(a,3)$ terletak di dalam lingkaran $x^2+y^2-5x-4y-3=0$. Dengan demikian batas-batas nilai $a$ adalah ...
Penyelesaian:
Titik $(a,3)\Rightarrow x=a,y=3$ terletak di dalam lingkaran $x^2+y^2-5x-4y-3=0$, maka:
$\begin{align}x^2+y^2-5x-4y-3 & < 0 \\ a^2+3^2-5.a-4.3-3 & < 0 \\ a^2+9-5a-12-3 & < 0 \\ a^2-5a-6 & < 0 \\ (a+1)(a-6) & < 0 \end{align}$
Pembuat nol: $a=-1$ atau $a=6$
Garis bilangan:
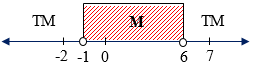
Titik (a,3) terletak di dalam lingkaran
$-1 < a < 6$
Jadi, agar titik $(a,3)$ terletak di dalam lingkaran ${{x}^{2}}+{{y}^{2}}-5x-4y-3=0$ maka batas-batas nilai $a$ adalah $-1 < a < 6$.

E. Jarak Titik $Q(x_1,y_1)$ terhadap lingkaran yang berpusat di $P(a,b)$ dan Berjari-jari r

Jarak titik $Q(x_1,y_1)$ terhadap lingkaran yang berpusat di $P(a,b)$ dan berjari-jari $r$ dapat ditentukan melalui posisi titik $Q(x_1,y_1)$ terhadap lingkaran.
1.Jika titik $Q(x_1,y_1)$ terletak pada lingkaran maka:
Jarak = 0
2.Jika titik $Q(x_1,y_1)$ terletak di dalam lingkaran maka:
Jarak terdekat = $|PQ-r|$
Jarak terjauh = $PQ+r$
3.Jika titik $Q(x_1,y_1)$ terletak di luar lingkaran maka:
Jarak terdekat = $|PQ-r|$
Jarak terjauh = $\sqrt{(PQ)^2-r^2}$
Contoh 1.
Tentukan jarak terdekat dan jarak terjauh titik $Q(5,-5)$ terhadap lingkaran $x^2+y^2+2x-6y-15=0$.
Penyelesaian:
$x^2+y^2+2x-6y-15=0$
$A=2$, $B=-6$ dan $C=-15$
Titik pusat lingkaran:
$P\left( \frac{A}{-2},\frac{B}{-2} \right)=P\left( \frac{2}{-2},\frac{-6}{-2} \right)=P\left( -1,3 \right)$
$\begin{align}r &= \sqrt{\frac{A^2}{4}+\frac{B^2}{4}-C} \\ &= \sqrt{\frac{2^2}{4}+\frac{(-6)^2}{4}+15} \\ r &= 5 \end{align}$
$\begin{align}PQ &= \sqrt{(x_Q-x_P)^2+(y_Q-y_P)^2} \\ &= \sqrt{(5+1)^2+(-5-3)^2} \\ PQ &= 10 \end{align}$
Substitusi titik $Q(5,-5)$ ke persamaan lingkaran:
$5^2+(-5)^2+2.5-6(-5)-15=75 > 0$, berarti titik Q di luar lingkaran.
Jarak terdekat = $|PQ-r|$ = $|10-5|$ = 5
Jarak terjauh = $\sqrt{(PQ)^2-r^2}$ = $\sqrt{10^2-5^2}$ = $5\sqrt{3}$.
Contoh 2.
Tentukan jarak terdekat dan jarak terjauh titik $Q(7,1)$ terhadap lingkaran $(x-4)^2+(y+3)^2=36$.
Penyelesaian:
Dari persamaan lingkaran $(x-4)^2+(y+3)^2=36$ diperoleh:
Titik pusat $P(4,-3)$ dan $r=6$
$\begin{align}PQ &= \sqrt{(x_Q-x_P)^2+(y_Q-y_P)^2} \\ &= \sqrt{(7-4)^2+(1+3)^2} \\ PQ &= 5 \end{align}$
Substitusi titik $Q(7,1)$ ke persamaan lingkaran:
$(7-4)^2+(1+3)^2=25 < 36$, berarti titik Q di dalam lingkaran.
Jarak terdekat = $|PQ-r|$ = $|5-6|$ = 1
Jarak terjauh = $PQ+r$ = 5 + 6 = 11

F. Soal Latihan Kedudukan Titik Terhadap Lingkaran

1.Tentukan kedudukan titik $C(3,-2)$, $I(6,1)$, $N(4,-1)$, $T(7,-1)$ dan $A(-2,3)$ terhadap lingkaran $(x-3)^2+(y+2)^2=17$.
2.Tentukan nilai $m$ agar titik $B(m-3,4)$ terletak pada lingkaran $x^2+y^2=41$.
3.Titik $(2,b)$ terletak di luar lingkaran $(x-2)^2+(y-4)^2=25$, tentukan batas-batas nilai $b$.
4.Tentukan nilai $a$ agar titik $A(a,5)$ terletak pada lingkaran $x^2+y^2-2x-10y+10=0$.
5.Titik $(a,-5)$ terletak di dalam lingkaran $x^2+y^2-14x+10y-95=0$, tentukan batas-batas nilai $a$.

Post a Comment for "Lingkaran 4. Kedudukan Titik Terhadap Lingkaran"

Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.