Vektor 2. Operasi pada Vektor

Pada postingan ini kita akan belajar mengenai Operasi pada Vektor yaitu Kesamaan Dua Vektor, Penjumlahan Dua Vektor, Pengurangan Dua Vektor dan Perkalian Skalar dengan Vektor.

A. Kesamaan Vektor

Kesamaan vektor secara geometri:
Dua vektor $\vec{a}$ dan $\vec{b}$ disebut sama, ditulis $\vec{a}=\vec{b}$, jika dan hanya jika keduanya sama besar (sama panjang) dan arahnya juga sama, sedangkan titik pangkalnya dan titik ujungnya tidak perlu sama.
Pada Gambar 1 diperlihatkan vektor $\overrightarrow{AB}$, $\overrightarrow{DC}$, $\overrightarrow{OP}$ dan $\overrightarrow{QR}$. Disini jelas bahwa $\overrightarrow{AB}=\overrightarrow{OP}$ dan $\overrightarrow{DC}=\overrightarrow{QR}$.
Pada Gambar 2 diperlihatkan bahwa $\overrightarrow{HA}=\overrightarrow{GB}$ dan $\overrightarrow{BD}=\overrightarrow{FH}$.

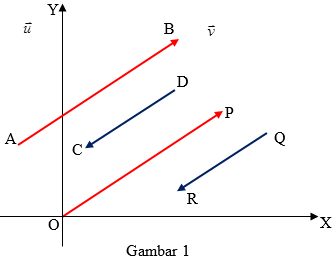
Kesamaan vektor secara aljabar:

1. Diketahui $\vec{a}=\left( \begin{matrix}x_1 \\ y_1 \\ \end{matrix} \right)$ dan $\vec{b}=\left( \begin{matrix}x_2 \\ y_2 \\ \end{matrix} \right)$. Jika $\vec{a}=\vec{b}$ maka $x_1=x_2$ dan $y_1=y_2$.
2. Diketahui $\vec{a}=\left( \begin{matrix}x_1 \\ y_1 \\ z_1 \\ \end{matrix} \right)$ dan $\vec{b}=\left( \begin{matrix}x_2 \\ y_2 \\ z_2 \\ \end{matrix} \right)$. Jika $\vec{a}=\vec{b}$ maka $x_1=x_2$, $y_1=y_2$dan $z_1=z_2$.

B. Penjumlahan dan Pengurangan Vektor

a. Penjumlahan dan Pengurangan Vektor secara Geometri

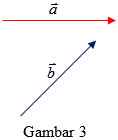
Penjumlahan dan pengurangan vektor secara geometri dapat ditentukan menggunakan dua metode yaitu metode jajaran genjang dan metode segitiga.
Metode Jajaran Genjang:
Diberikan dua vektor $\vec{a}$ dan $\vec{b}$ (Gambar 3). Tentukan vektor $\vec{a}+\vec{b}$ dan vektor $\vec{a}-\vec{b}$.
Penyelesaian:
Penjumlahan vektor ($\vec{a}+\vec{b}$)
Langkah-langkah metode jajaran genjang:

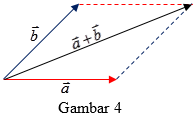
1. Lukis vektor $\vec{a}$.
2. Impitkan titik pangkal vektor $\vec{b}$ dengan titik pangkal vektor $\vec{a}$.
3. Tarik garis putus-putus dari ujung vektor $\vec{a}$ sejajar dengan vektor $\vec{b}$ dan dari ujung vektor $\vec{b}$ sejajar dengan vektor $\vec{a}$, sehingga kedua garis tersebut berpotongan.
4. Tarik garis lurus dari titik pangkal kedua vektor $\vec{a}$ dan $\vec{b}$ ke titik potong garis putus-putus itu, sehingga diperoleh segmen garis yang merupakan jumlah vektor $\vec{a}$ dan $\vec{b}$, yaitu $\vec{a}+\vec{b}$ (Gambar 4).

Pengurangan vektor ($\vec{a}-\vec{b}$)
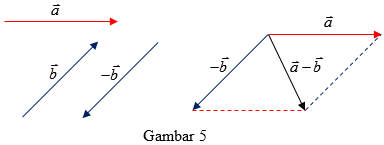
Selisih $\vec{a}$ dan $\vec{b}$ ditulis $\vec{a}-\vec{b}$ dapat juga ditulis sebagai $\vec{a}+(-\vec{b})$, dimana vektor $-\vec{b}$ adalah vektor yang berlawanan arah dengan vektor $\vec{b}$. Dengan menggunakan langkah-langkah pada penjumlahan vektor, akan diperoleh hasilnya seperti Gambar 5.

Metode Segitiga:
Diberikan dua vektor $\vec{a}$ dan $\vec{b}$ (Gambar 6). Tentukan vektor $\vec{a}+\vec{b}$ dan vektor $\vec{a}-\vec{b}$.
Penyelesaian:
Penjumlahan vektor ($\vec{a}+\vec{b}$)
Langkah-langkah metode segitiga:

1. Lukislah vektor $\vec{a}$.
2. Impitkan pangkal vektor $\vec{b}$ ke ujung vektor $\vec{a}$.
3. Tarik garis lurus dari pangkal vektor $\vec{a}$ ke ujung vektor $\vec{b}$, sehingga diperoleh segmen garis yang merupakan jumlah vektor $\vec{a}$ dan $\vec{b}$ yaitu $\vec{a}+\vec{b}$ (Gambar 7).

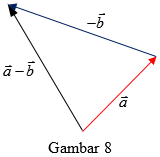
Pengurangan vektor ($\vec{a}-\vec{b}$)
Dengan cara yang sama dapat ditentukan vektor $\vec{a}-\vec{b}$, dimana $\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$ (Gambar 8).

Panjang vektor hasil penjumlahan dan pengurangan:
Jika diketahui $\left| {\vec{a}} \right|$, $\left| {\vec{b}} \right|$ dan $\angle (\vec{a},\vec{b})=\theta $, dengan menggunakan aturan cosinus maka:

1. $\left| \vec{a}+\vec{b} \right|=\sqrt{\left| {\vec{a}} \right|^2+\left| {\vec{b}} \right|^2+2\left| {\vec{a}} \right|\left| {\vec{b}} \right|\cos \theta }$
2. $\left| \vec{a}-\vec{b} \right|=\sqrt{\left| {\vec{a}} \right|^2+\left| {\vec{b}} \right|^2-2\left| {\vec{a}} \right|\left| {\vec{b}} \right|\cos \theta }$

b. Penjumlahan dan Pengurangan Vektor secara Aljabar

Jika vektor di $R^2$ yaitu $\vec{a}=\left( \begin{matrix}x_1 \\ x_2 \\ \end{matrix} \right)$ dan $\vec{b}=\left( \begin{matrix} x_2 \\ y_2 \\ \end{matrix} \right)$ maka:
$\vec{a}+\vec{b}=\left( \begin{matrix}x_1+x_2 \\ y_1 + y_2 \\ \end{matrix} \right)$ dan $\vec{a}-\vec{b}=\left( \begin{matrix}x_1-x_2 \\ y_1-y_2 \\ \end{matrix} \right)$
Jika vektor di $R^3$ yaitu $\vec{a}=\left( \begin{matrix} x_1 \\ y_1 \\ z_1 \\ \end{matrix} \right)$ dan $\vec{b}=\left( \begin{matrix}x_2 \\ y_2 \\ z_2 \\ \end{matrix} \right)$ maka:
$\vec{a}+\vec{b}=\left( \begin{matrix}x_1+x_2 \\ y_1+y_2 \\ z_1+z_2 \\ \end{matrix} \right)$ dan $\vec{a}-\vec{b}=\left( \begin{matrix}x_1-x_2 \\ y_1-y_2 \\ z_1-z_2 \\ \end{matrix} \right)$

Contoh 1.
Diketahui kubus ABCD.EFGH. Jika $\overrightarrow{AB}=\vec{a}$, $\overrightarrow{BC}=\vec{b}$ dan $\overrightarrow{AE}=\vec{c}$. Nyatakan vektor $\overrightarrow{AG}$ dalam $\vec{a}$, $\vec{b}$ dan $\vec{c}$
Penyelesaian:
Perhatikan gambar berikut!
Berdasarkan konsep kesamaan vektor maka:
$\overrightarrow{CG}=\overrightarrow{AE}=\vec{a}$
Dengan metode segitiga maka:
$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$
$\begin{align}\overrightarrow{AG} &= \overrightarrow{AC}+\overrightarrow{CG} \\ &= \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CG} \\ \overrightarrow{AG} &= \vec{a}+\vec{b}+\vec{c} \end{align}$

Contoh 2.
Diketahui $\vec{a}=2\hat{i}+x\hat{j}+y\hat{k}$, $\vec{b}=y\hat{i}+2\hat{j}+z\hat{k}$ dan $\vec{c}=x\hat{i}+z\hat{j}+2\hat{k}$. Jika $\vec{a}+\vec{b}=\vec{c}$ maka nilai $x$, $y$, dan $z$ berturut-turut adalah ...
Penyelesaian:
$\begin{align}\vec{a}+\vec{b} &= \vec{c} \\ \left( \begin{matrix} 2 \\ x \\ y \\ \end{matrix} \right)+\left( \begin{matrix} y \\ 2 \\ z \\ \end{matrix} \right) &= \left( \begin{matrix} x \\ z \\ 2 \\ \end{matrix} \right) \\ \left( \begin{matrix} 2+y \\ x+2 \\ y+z \\ \end{matrix} \right) &= \left( \begin{matrix} x \\ z \\ 2 \\ \end{matrix} \right) \end{align}$
$2+y=x$ .... (1)
$\begin{align}x+2 &= z \\ 2+y+2 &= z \\ y+4 &= z\,....\,(2) \end{align}$
$\begin{align}y+z &= 2 \\ y+y+4 &= 2 \\ 2y &= -2 \\ y &= -1 \end{align}$
Substitusi $y=-1$ ke persamaan (1) maka:
$\begin{align}2+y &= x \\ 2+(-1) &= x \\ 1 &= x \end{align}$
Substitusi $y=-1$ ke persamaan (2) maka:
$\begin{align}y+4 &= z \\ -1+4 &= z \\ 3 &= z \end{align}$
Jadi, nilai $x=1$, $y=-1$ dan $z=3$.

Contoh 3.
Jika $\left| {\vec{a}} \right|=2$, $\left| {\vec{b}} \right|=3$, dan sudut yang dibentuk vektor $\vec{a}$ dan $\vec{b}$ adalah $120^\circ $, maka $\left| 3\vec{a}+2\vec{b} \right|$ adalah ...
Penyelesaian:
$\left| {\vec{a}} \right|=2\Rightarrow \left| 3\vec{a} \right|=6$
$\left| {\vec{b}} \right|=3\Rightarrow \left| 2\vec{b} \right|=6$
$\theta =\angle (\vec{a},\vec{b})=120^\circ $
Panjang vektor hasil penjumlahan vektor $3\vec{a}$ dan $2\vec{b}$ adalah:
$\begin{align}\left| 3\vec{a}+2\vec{b} \right| &= \sqrt{\left| 3\vec{a} \right|^2+\left| 2\vec{b} \right|^2+2.\left| 3\vec{a} \right|.\left| 2\vec{b} \right|.\cos \theta } \\ &= \sqrt{6^2+6^2+2.6.6.\cos 120^\circ } \\ &= \sqrt{36+36+72.\left( -\frac{1}{2} \right)} \\ \left| 3\vec{a}+2\vec{b} \right| &= 6 \end{align}$

C. Perkalian Vektor dengan Skalar (Bilangan Real)

1. Misalkan $m$ adalah bilangan real dan $\vec{a}=\left( \begin{matrix} x \\ y \\ \end{matrix} \right)$ maka $m\vec{a}=m\left( \begin{matrix} x \\ y \\ \end{matrix} \right)=\left( \begin{matrix} mx \\ my \\ \end{matrix} \right)$.
2. Misalkan $m$ adalah bilangan real dan $\vec{a}=\left( \begin{matrix} x \\ y \\ z \\ \end{matrix} \right)$ maka $m\vec{a}=m\left( \begin{matrix} x \\ y \\ z \\ \end{matrix} \right)=\left( \begin{matrix} mx \\ my \\ mz \\ \end{matrix} \right)$

Contoh 4.
Diketahui vektor $\vec{a}=\left( \begin{matrix} 2 \\ 4 \\ 5 \\ \end{matrix} \right)$, $\vec{b}=\left( \begin{matrix} -1 \\ -2 \\ 0 \\ \end{matrix} \right)$, $\vec{c}=\left( \begin{matrix} 0 \\ 2 \\ 3 \\ \end{matrix} \right)$, maka $2\vec{a}-3b+5\vec{c}$ = ....
Penyelesaian:
$\begin{align}2\vec{a}-3b+5\vec{c} &= 2\left( \begin{matrix} 2 \\ 4 \\ 5 \\ \end{matrix} \right)-3\left( \begin{matrix} -1 \\ -2 \\ 0 \\ \end{matrix} \right)+5\left( \begin{matrix} 0 \\ 2 \\ 3 \\ \end{matrix} \right) \\ &= \left( \begin{matrix} 4 \\ 8 \\ 10 \\ \end{matrix} \right)-\left( \begin{matrix} -3 \\ -6 \\ 0 \\ \end{matrix} \right)+\left( \begin{matrix} 0 \\ 10 \\ 15 \\ \end{matrix} \right) \\ 2\vec{a}-3b+5\vec{c} &= \left( \begin{matrix} 4-(-3)+0 \\ 8-(-6)+10 \\ 10-0+15 \\ \end{matrix} \right) \\ &= \left( \begin{matrix} 7 \\ 24 \\ 25 \\ \end{matrix} \right) \end{align}$

D. Soal Latihan

1. Diketahui titik $A(3,-2,4)$, $B(1,3,-2)$ dan $C(x,2,4)$. Vektor $\vec{u}$ adalah wakil dari $\overrightarrow{AB}$ dan $\vec{v}$ adalah wakil dari $\overrightarrow{AC}$. Jika $\overrightarrow{AC}=\overrightarrow{AB}$, maka $x$ = ...
2. Jika $\vec{a}=\left( \begin{matrix} 3 \\ -2 \\ \end{matrix} \right)$, $\vec{b}=\left( \begin{matrix} 1 \\ 0 \\ \end{matrix} \right)$ dan $\vec{c}=\left( \begin{matrix} -5 \\ 4 \\ \end{matrix} \right)$, tentukan panjang vektor $\vec{d}=\vec{a}+\vec{b}-\vec{c}$.
3. Jika $\overrightarrow{AB}=\left( \begin{matrix} 1 \\ 3 \\ 6 \\ \end{matrix} \right)$, tentukan vektor $4\overrightarrow{AB}$.
4. Diketahui $\left| {\vec{a}} \right|=7$, $\left| {\vec{b}} \right|=8$, dan besar sudut antara vektor $\vec{a}$ dan $\vec{b}$ ditulis $\angle (\vec{a},\vec{b})=60{}^\circ $. Tentukan panjang vektor $(\vec{a}+\vec{b})$.
5. Diketahui $\left| {\vec{u}} \right|=7$, $\left| {\vec{v}} \right|=8$, dan besar sudut antara vektor $\vec{a}$ dan $\vec{b}$ ditulis $\angle (\vec{a},\vec{b})=120{}^\circ $. Tentukan panjang vektor $(\vec{u}+\vec{v})$.

Semoga postingan: Vektor 2. Operasi pada Vektor ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :