Vektor 3. Perbandingan Vektor

A. Pembagian Ruas Garis

Suatu titik P membagi ruas garis AB dengan perbandingan $m:n$, sehingga $AP:PB=m:n$. Bila titik P di dalam AB, maka $\overrightarrow{AB}$ dan $\overrightarrow{PB}$ mempunyai arah yang sama sehingga $m$ dan $n$ mempunyai tanda yang sama. Perhatikan gambar berikut!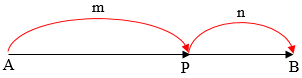

• $\overrightarrow{AP}:\overrightarrow{PB}=m:n$
• $\overrightarrow{AP}:\overrightarrow{AB}=m:(m+n)$
• $\overrightarrow{PB}:\overrightarrow{AB}=n:(m+n)$

Suatu titik P membagi ruas garis AB dengan perbandingan $m:n$, sehingga $AP:PB=m:n$. Bila titik P di luar AB, maka $\overrightarrow{AB}$ dan $\overrightarrow{PB}$ mempunyai arah yang berlawanan sehingga $m$ dan $n$ mempunyai tanda yang berlawanan. Perhatikan gambar berikut!

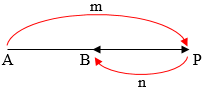
• $\overrightarrow{AP}:\overrightarrow{PB}=m:(-n)$
• $\overrightarrow{AP}:\overrightarrow{AB}=m:(m-n)$
• $\overrightarrow{PB}:\overrightarrow{AB}=n:(m-n)$

Vektor-vektor Segaris (Kolinear)
Titik-titik A, B, dan C dikatakan segaris (kolinear), jika dan hanya jika $\overrightarrow{AB}=k.\overrightarrow{BC}$, atau vektor $\vec{a}$ dan vektor $\vec{b}$ dikatakan segaris (kolinear), jika dan hanya jika $\vec{a}=k\vec{b}$, dengan $k$ bilangan real.

---

B. Pembagian dalam Bentuk Vektor

Jika $\vec{a}$, $\vec{b}$, dan $\vec{p}$ berturut-turut menyatakan vektor posisi dari titik A, B, dan P dengan titik P membagi ruas garis $\overrightarrow{AB}$ dan $\overrightarrow{AP}:\overrightarrow{PB}=m:n$, maka berlaku: $\vec{p}=\frac{m\vec{b}+n\vec{a}}{m+n}$

Bukti:
$\begin{align}\overrightarrow{AP}:\overrightarrow{PB} &= m:n \\ \frac{\overrightarrow{AP}}{\overrightarrow{PB}} &= \frac{m}{n} \\ n\overrightarrow{AP} &= m\overrightarrow{PB} \\ n\left( \overrightarrow{OP}-\overrightarrow{OA} \right) &= m\left( \overrightarrow{OB}-\overrightarrow{OP} \right) \\ n(\vec{p}-\vec{a}) &= m(\vec{b}-\vec{p}) \\ n\vec{p}-n\vec{a} &= m\vec{b}-m\vec{p} \\ m\vec{p}+n\vec{p} &= m\vec{b}+n\vec{a} \\ \vec{p}(m+n) &= m\vec{b}+n\vec{a} \\ \vec{p} &= \frac{m\vec{b}+n\vec{a}}{m+n} \end{align}$

---

Contoh 1.
Jika titik P membagi garis hubung $A(0,-4,5)$ dan $B(0,1,5)$ di dalam perbandingan $2:3$, maka koordinat titik P adalah ...
Penyelesaian:
$\vec{a}=\overrightarrow{OA}=(0,-4,5)$
$\vec{b}=\overrightarrow{OB}=(0,1,5)$
$\vec{p}=\overrightarrow{OP}$
$\begin{align}\overrightarrow{AP}:\overrightarrow{PB} &= 2:3 \\ \overrightarrow{AP}:\overrightarrow{PB} &= m:n \\ \end{align}$
$\begin{align}\vec{p} &= \frac{m\vec{b}+n\vec{a}}{m+n} \\ &= \frac{2\vec{b}+3\vec{a}}{2+3} \\ &= \frac{2(0,1,5)+3(0,-4,5)}{5} \\ &= \frac{(0,2,10)+(0,-12,15)}{5} \\ &= \frac{(0,-10,25)}{5} \\ \vec{p} &= (0,-2,5) \end{align}$
Jadi, titik $P(0,-2,5)$

---

Contoh 2.
Diketahui titik $A(1,8,-3)$, $B(1,2,3)$ dan $AP:PB=3:1$. Jika titik P berada pada perpanjangan garis AB, maka koordinat titik P adalah ...
Penyelesaian:
Perhatikan gambar berikut:
Dari gambar:
$\overrightarrow{AP}:\overrightarrow{PB}=3:(-1)$
$AP:PB=m:n$
$\begin{align}\vec{p} &= \frac{m\vec{b}+n\vec{a}}{m+n} \\ &= \frac{3\vec{b}-\vec{a}}{3-1} \\ &= \frac{3(1,2,3)-(1,8,-3)}{2} \\ &= \frac{(3,6,9)-(1,8,-3)}{5} \\ &= \frac{(2,-2,12)}{2} \\ \vec{p} &= (1,-1,6) \end{align}$
Koordinat titik $P(1,-1,6)$.

---

Contoh 3.
Diketahui titik $A(x,y,4)$, $B(3,2,1)$ dan $C(-3,5,10)$ segaris (kolinear). Tentukan nilai $x$ dan $y$.
Penyelesaian:
Titik A, B, dan C kolinear maka:
$\begin{align}\overrightarrow{AB} &= k.\overrightarrow{BC} \\ \overrightarrow{OB}-\overrightarrow{OA} &= k\left( \overrightarrow{OC}-\overrightarrow{OB} \right) \\ \left( \begin{matrix} 3 \\ 2 \\ 1 \\ \end{matrix} \right)-\left( \begin{matrix} x \\ y \\ 4 \\ \end{matrix} \right) &= k\left( \left( \begin{matrix} -3 \\ 5 \\ 10 \\ \end{matrix} \right)-\left( \begin{matrix} 3 \\ 2 \\ 1 \\ \end{matrix} \right) \right) \\ \left( \begin{matrix} 3-x \\ 2-y \\ -3 \\ \end{matrix} \right) &= k\left( \begin{matrix} -6 \\ 3 \\ 9 \\ \end{matrix} \right) \\ \left( \begin{matrix} 3-x \\ 2-y \\ -3 \\ \end{matrix} \right) &= \left( \begin{matrix} -6k \\ 3k \\ 9k \\ \end{matrix} \right) \end{align}$
$\begin{align}9k &= -3 \\ k &= \frac{-3}{9} \\ k &= -\frac{1}{3} \end{align}$
$\begin{align}-6k &= 3-x \\ x &= 3+6k \\ &= 3+6.\left( -\frac{1}{3} \right) \\ &= 3-2 \\ x &= 1 \end{align}$
$\begin{align}3k &= 2-y \\ y &= 2-3k \\ &= 2-3.\left( -\frac{1}{3} \right) \\ &= 2+1 \\ y &= 3 \end{align}$
Jadi, nilai $x=1$ dan $y=3$

---

C. Soal Latihan

1. Diketahui titik-titik $P(1,-2,1)$ dan $Q(7,-5,1)$. Jika T pada ruas garis PQ dan PT : TQ = 1 : 2. Tentukan koordinat titik T.
2. Diketahui titik-titik $A(1,-2,-8)$ dan $B(3,-4,0)$. Titik P terletak pada perpanjangan AB sehingga $\overrightarrow{AP}=-3\overrightarrow{PB}$. Tentukan koordinat titik P.
3. Diketahui titik-titik $A(1,4,6)$, $B(1,0,2)$ dan $C(2,-1,5)$. Titik P terletak pada perpanjangan AB sedemikian sehingga $AP:PB=3:1$. Tentukan vektor yang mewakili $\overrightarrow{PC}$.
4. Diketahui titik $A(4,7,2)$, $B(5,8,3)$, dan $C(2,5,0)$ segaris (kolinear). Tentukan nilai perbandingan $\overrightarrow{AB}:\overrightarrow{BC}$.
5. Titik $A(3,2,-1)$, $B(1,-2,1)$, dan $C(7,p-1,-5)$ segaris (kolinear). Tentukan nilai $p$.

Semoga postingan: Vektor 3. Perbandingan Vektor ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :