Lingkaran 6. Kedudukan Dua Lingkaran

A. Kedudukan Dua Lingkaran

1. Dua lingkaran yang sepusat

Dua buah lingkaran dikatakan sepusat jika koordinat titik pusatnya sama.

2. Dua lingkaran yang bersinggungan

Misalkan lingkaran $L_1$ mempunyai titik pusat $P_1$ dan jari-jari $r_1$ dan lingkaran $L_2$ mempunyai titik pusat $P_2$ dan jari-jari $r_2$ maka:
1) Dua lingkaran bersinggungan di dalam
Perhatikan gambar berikut!

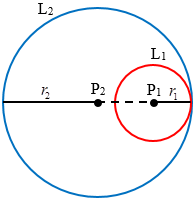
Lingkaran $L_1$ dan $L_2$ bersinggungan di dalam jika $\left| P_1P_2 \right|=\left| r_1-r_2 \right|$.

2) Dua lingkaran bersinggungan di luar
Perhatikan gambar berikut!

Lingkaran $L_1$ dan $L_2$ bersinggungan di luar jika $\left| P_1P_2 \right|=r_1+r_2$.

3. Lingkaran yang satu berada di dalam lingkaran yang lain.

Perhatikan gambar berikut!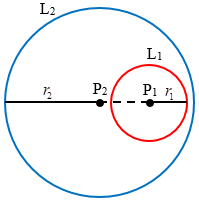

Lingkaran $L_1$ di dalam lingkaran $L_2$ jika $\left| P_1P_2 \right| \le \left| r_1-r_2 \right|$.

4. Dua lingkaran yang saling lepas

Perhatikan gambar berikut!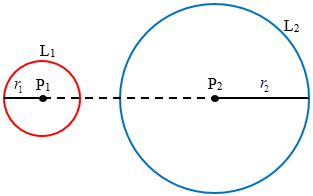

Lingkaran $L_1$ dan $L_2$ saling lepas ($L_1$ dan $L_2$ tidak bersinggungan maupun berpotongan) jika $\left| P_1P_2 \right| > r_1+r_2$.

5. Dua lingkaran saling berpotongan

Perhatikan gambar berikut!

Lingkaran $L_1$ dan $L_2$ saling berpotongan jika $\left| r_1-r_2 \right| < \left| P_1P_2 \right| < r_1+r_2$.

6. Dua lingkaran ortogonal

Perhatikan gambar berikut!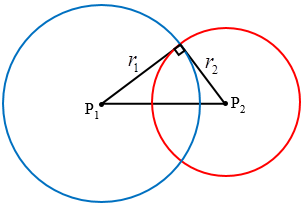

Lingkaran $L_1$ dan $L_2$ ortogonal jika $\left| P_1P_2 \right|^2=r_1^2+r_2^2$.

B. Persamaan Garis (Tali Busur) dari Dua Lingkaran yang berpotongan

Perhatikan gambar berikut!

$L_1$ adalah persamaan lingkaran dengan pusat $P_1$ dan jari-jari $r_1$.
$L_2$ adalah persamaan lingkaran dengan pusat $P_2$ dan jari-jari $r_2$.
Persamaan garis (tali busur) $L_1$ dan $L_2$ adalah:
$L_1-L_2=0$
Panjang garis (tali busur) yaitu jarak antara dua titik potong lingkaran $L_1$ dan $L_2$. Berdasarkan gambar panjang tali busur adalah adalah (AB = 2AQ), dimana:
$AB=2\sqrt{r_1^2-\left( P_1Q \right)^2}$ atau $AB=2\sqrt{r_2^2-\left( P_2Q \right)^2}$

C. Contoh Soal dan Pembahasan

Contoh 1.
Tentukan kedudukan dua buah lingkaran yaitu $L_1 \equiv x^2+y^2-10x+2y+17=0$ dan $L_2 \equiv x^2+y^2+8x-22y-7=0$.
Penyelesaian:
$L_1 \equiv x^2+y^2-10x+2y+17=0$
A = -10, B = 2, C = 17
$P_1\left( \frac{A}{-2},\frac{B}{-2} \right)=P_1\left( \frac{-10}{-2},\frac{2}{-2} \right)=P_1\left( 5,-1 \right)$
$\begin{align}r_1 &= \sqrt{\frac{A^2}{4}+\frac{B^2}{4}-C} \\ &= \sqrt{\frac{\left( -10 \right)^2}{4}+\frac{2^2}{4}-17} \\ &= \sqrt{25+1-17} \\ &= \sqrt{9} \\ r_1 &= 3 \end{align}$
$L_2 \equiv x^2+y^2+8x-22y-7=0$
A = 8, B = -22, C = -7
$P_2\left( \frac{A}{-2},\frac{B}{-2} \right)=P_2\left( \frac{8}{-2},\frac{-22}{-2} \right)=P_2\left( -4,11 \right)$
$\begin{align}r_2 &= \sqrt{\frac{A^2}{4}+\frac{B^2}{4}-C} \\ &= \sqrt{\frac{8^2}{4}+\frac{(-22)^2}{4}-(-7)} \\ &= \sqrt{16+121+7} \\ &= \sqrt{144} \\ r_2 &= 12 \end{align}$
$\begin{align}\left| P_1P_2 \right| &= \sqrt{\left( -4-5 \right)^2+\left( 11+1 \right)^2} \\ &= \sqrt{81+144} \\ &= \sqrt{225} \\ \left| P_1P_2 \right| &= 15 \end{align}$
$r_1+r_2=3+12=15$
Karena $\left| P_1P_2 \right|=r_1+r_2$ maka $L_1$ dan $L_2$ bersinggungan di luar.

---

Contoh 2.
Tentukan persamaan lingkaran dengan jari-jari 5 satuan dan bersinggungan di luar lingkaran dengan persamaan $x^2+y^2-2x-4y-20=0$ di titik $A(5,5)$.
Penyelesaian:
Misal:
$L_1$ adalah lingkaran dengan pusat $P_1(a,b)$ dan $r_1=5$.
$L_1 \equiv (x-a)^2+(y-b)^2=5^2$ melalui titik $A(5,5)$ maka:
$\begin{align}(5-a)^2+(5-b)^2 &= 5^2 \\ 25-10a+a^2+25-10b+b^2 &= 25 \\ a^2+b^2-10a-10b+25 &= 0\,......\,(1) \end{align}$
$\begin{align}L_2 &\equiv x^2+y^2-2x-4y-20=0 \\ &\equiv x^2-2x+y^2-4y=20 \\ &\equiv \left( x-\frac{2}{2} \right)^2-\left( \frac{2}{2} \right)^2+\left( y-\frac{4}{2} \right)^2-\left( \frac{4}{2} \right)^2=20 \\ &\equiv \left( x-1 \right)^2-1+\left( y-2 \right)^2-4=20 \\ L_2 &\equiv \left( x-1 \right)^2+\left( y-2 \right)^2 = 5^2 \end{align}$
$L_2$ adalah lingkaran dengan pusat $P_2(1,2)$ dan $r_2=5$.
$L_1$ dan $L_2$ bersinggungan di luar, maka:
$\begin{align}\left| P_1P_2 \right| &= r_1+r_2 \\ \sqrt{(1-a)^2+(2-b)^2} &= 5+5 \\ 1-2a+a^2+4-4b+b^2 &= 100 \\ a^2+b^2-2a-4b-95 &= 0\,......\,(2) \end{align}$
Kurangkan persamaan (1) dengan (2):
$\begin{align}a^2+b^2-10a-10b+25 &= 0 \\ a^2+b^2-2a-4b-95 &= 0 \end{align}$
--------------------------------------------------- (-)
$\begin{align}-8a-6b+120 &= 0 \\ 4a+3b-60 &= 0 \\ 4a &= 60-3b \\ a &= \frac{60-3b}{4}\,......\,(3) \end{align}$
Substitusi ke persamaan (2):
$a^2+b^2-2a-4b-95=0$
$\left( \frac{60-3b}{4} \right)^2+b^2-2\left( \frac{60-3b}{4} \right)-4b-95=0$
$\frac{3600-360b+9b^2}{16}+b^2-\frac{120-6b}{4}-4b-95=0$
$3600-360b+9b^2+16b^2-(480-24b)-64b-1520=0$
$25b^2-400b+1600=0$
$b^2-16b+64=0$
$(b-8)^2=0$
$b=8$
Substitusi ke persamaan (3):
$\begin{align}a &= \frac{60-3b}{4} \\ &= \frac{60-3.8}{4} \\ a &= 9 \end{align}$
Jadi, persamaan lingkaran ${{L}_{1}}$ dengan pusat $(a,b)=(9,8)$ dan $r=5$ adalah:
$\begin{align}(x-a)^2+(y-b)^2 &= r^2 \\ (x-9)^2+(y-8)^2 &= 5^2 \\ x^2-18x+81+y^2-16y+64 &= 25 \\ x^2+y^2-18x-16y+120 &= 0 \end{align}$

---

Contoh 3.
Tentukan persamaan lingkaran berjari-jari 3 satuan dan bersinggungan di dalam dengan lingkaran $x^2+y^2-4x-6y-12=0$ di titik $(-1,-1)$.
Penyelesaian:
$L_1$ adalah lingkaran dengan pusat $P_1(a,b)$ dan $r_1=3$.
$L_1 \equiv (x-a)^2+(y-b)^2=9$ melalui titik $(-1,-1)$ maka:
$\begin{align}(x-a)^2+(y-b)^2 &= 9 \\ (-1-a)^2+(-1-b)^2 &= 9 \\ 1+2a+a^2+1+2b+b^2 &= 9 \\ a^2+b^2+2a+2b-7 &= 0\,......\,(1) \end{align}$
$\begin{align}L_2 &\equiv x^2+y^2-4x-6y-12=0 \\ &\equiv x^2-4x+y^2-6y=12 \\ &\equiv \left( x-\frac{4}{2} \right)^2-\left( \frac{4}{2} \right)^2+\left( y-\frac{6}{2} \right)^2-\left( \frac{6}{2} \right)^2=12 \\ &\equiv \left( x-2 \right)^2-4+\left( y-3 \right)^2-9=12 \\ L_2 &\equiv \left( x-2 \right)^2+\left( y-3 \right)^2 = 5^2 \end{align}$
$L_2$ adalah lingkaran dengan pusat $P_2(2,3)$ dan $r_2=5$.
$L_1$ dan $L_2$ bersinggungan di dalam maka:
$\begin{align}\left| P_1P_2 \right| &= \left| r_1-r_2 \right| \\ \sqrt{(2-a)^2+(3-b)^2} &= \left| 3-5 \right| \\ (2-a)^2+(3-b)^2 &= 4 \\ 4-4a+a^2+9-6b+b^2 &= 4 \\ a^2+b^2-4a-6b+9 &= 0\,......\,(2) \end{align}$
Kurangkan persamaan (1) dengan persamaan (2):
$\begin{align}a^2+b^2+2a+2b-7 &= 0 \\ a^2+b^2-4a-6b+9 &= 0 \end{align}$
-------------------------------------------- (-)
$\begin{align}6a+8b-16 &= 0 \\ 3a+4b-8 &= 0 \\ 3a &= 8-4b \\ a &= \frac{8-4b}{3}\,......\,(3) \end{align}$
Substitusi ke persamaan (1):
$a^2+b^2+2a+2b-7=0$
$\left( \frac{8-4b}{3} \right)^2+b^2+2\left( \frac{8-4b}{3} \right)+2b-7=0$
$\frac{64-64b+16b^2}{9}+b^2+\frac{16-8b}{3}+2b-7=0$
$64-64b+16b^2+9b^2+48-24b+18b-63=0$
$25b^2-70b+49=0$
$(5b-7)^2=0$
$5b-7=0$
$b=\frac{7}{5}$
Substitusi ke persamaan (3):
$\begin{align}a &= \frac{8-4b}{3} \\ &= \frac{8-4.\frac{7}{5}}{3} \\ a &= \frac{4}{5} \end{align}$
Jadi, persamaan lingkaran $L_1$ dengan pusat $(a,b)=\left( \frac{4}{5},\frac{7}{5} \right)$ dan $r=3$ adalah:
$\begin{align}(x-a)^2+(y-b)^2 &= r^2 \\ \left( x-\frac{4}{5} \right)^2+\left( y-\frac{7}{5} \right)^2 &= 3^2 \\ x^2-\frac{8}{5}x+\frac{16}{25}+y^2-\frac{14}{5}y+\frac{49}{25} &= 9 \\ 25x^2-40x+16+25y^2-70y+49 &= 225 \\ 25x^2+25y^2-40x-70y-180 &= 0 \\ 5x^2+5y^2-8x-14y-36 &= 0\end{align}$

---

Contoh 4.
Diberikan dua lingkaran yaitu $L_1 \equiv (x-1)^2+(y-3)^2=r^2$ dan $L_2\equiv x^2+y^2-8x+2y+8=0$. Jika $L_1$ dan $L_2$ berpotongan di dua titik. Tentukan batas-batas nilai $r$.
Penyelesaian:
$L_1 \equiv (x-1)^2+(y-3)^2=r^2$ maka $P_1(1,3)$ dan $r_1=r$
$\begin{align}L_2 &\equiv x^2+y^2-8x+2y+8=0 \\ &\equiv x^2-8x+y^2+2y+8=0 \\ &\equiv \left( x-\frac{8}{2} \right)^2-\left( \frac{8}{2} \right)^2+\left( y+\frac{2}{2} \right)^2-\left( \frac{2}{2} \right)^2 = -8 \\ &\equiv \left( x-4 \right)^2-16+\left( y+1 \right)^2-1 = -8 \\ L_2 &\equiv \left( x-4 \right)^2+\left( y+1 \right)^2 = 3^2 \end{align}$
$P_2(4,-1)$ dan $r_2=3$
$L_1$ dan $L_2$ berpotongan di dua titik maka:
$\left| r_1-r_2 \right| < \left| P_1P_2 \right| < r_1+r_2$
$\left| r-3 \right| < \sqrt{(4-1)^2+(-1-3)^2} < r+3$
$\left| r-3 \right| < \sqrt{9+16} < r+3$
$\left| r-3 \right| < 5 < r+3$
i) $\left| r-3 \right| < 5$
$\begin{align}-5 < & r-3 < 5 \\ -5+3 < & r-3+3 < 5+3 \\ -2 < & r < 8 \end{align}$
ii) $r+3 > 5\Leftrightarrow r > 2$
Garis bilangan:

Jadi, batas-batas nilai $r$ yang memenuhi adalah $2 < r < 8$.

---

Contoh 5.
Tentukan persamaan tali busur dan panjang tali busur dari lingkaran $L_1 \equiv x^2+y^2+2x+3y+1=0$ dan $L_2 \equiv x^2+y^2+4x+3y+2=0$.
Penyelesaian:
Persamaan tali busur:
$L_1-L_2=0$
$L_1 \equiv x^2+y^2+2x+3y+1=0$
$L_2 \equiv x^2+y^2+4x+3y+2=0$
------------------------------------------------------ (-)
$\begin{align}-2x-1 &= 0 \\ -2x &= 1 \\ x &= -\frac{1}{2} \end{align}$
Jadi, persamaan tali busur kedua lingkaran adalah $x=-\frac{1}{2}$.
Selanjurnya untuk menentukan panjang tali busur kedua lingkaran, substitusi $x=-\frac{1}{2}$ ke salah satu persamaan lingkaran untuk menentukan kedua titik potong.
$L_1 \equiv x^2+y^2+2x+3y+1=0$
$\left( -\frac{1}{2} \right)^2+y^2+2\left( -\frac{1}{2} \right)+3y+1=0$
$\frac{1}{4}+y^2-1+3y+1=0$
$y^2+3y+\frac{1}{4}=0$
$4y^2+12y+1=0$
$\begin{align}y &= \frac{-12\pm \sqrt{{12}^2-4.4.1}}{2.4} \\ &= \frac{-12\pm \sqrt{128}}{8} \\ &= \frac{-12\pm 8\sqrt{2}}{8} \\ y &= \frac{-3\pm 2\sqrt{2}}{2} \\ \end{align}$
Diperoleh titik potong lingkaran adalah $\left( -\frac{1}{2},\frac{-3-2\sqrt{2}}{2} \right)$ dan $\left( -\frac{1}{2},\frac{-3+2\sqrt{2}}{2} \right)$
Panjang tali busur adalah jarak kedua titik potong lingkaran $L_1$ dan $L_2$ yaitu:
= $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
= $\sqrt{\left( -\frac{1}{2}+\frac{1}{2} \right)^2+\left( \frac{-3+2\sqrt{2}}{2}-\frac{-3-2\sqrt{2}}{2} \right)^2}$
= $\sqrt{0+\left( \frac{4\sqrt{2}}{2} \right)^2}$
= $2\sqrt{2}$
Jadi, panjang tali busur kedua lingkaran adalah $2\sqrt{2}$.

D. Soal Latihan

1. Diketahui dua buah lingkaran, yaitu $L_1 \equiv x^2+y^2-10x+2y+17=0$ dan $L_2 \equiv x^2+y^2+8x-22y-7=0$. Tentukan kedudukan kedua lingkaran tersebut.
2. Lingkaran $x^2+y^2+20x-12y+72=0$ dan lingkaran $x^2+y^2-4x-2y+11=0$. Tentukan kedudukan kedua lingkaran tersebut.
3. Tentukan kedudukan antara lingkaran $x^2+y^2+6x-4y-23=0$ dan $x^2+y^2-12x+20y+55=0$.
4. Lingkaran A dengan persamaan $x^2+y^2-8x+6y+1=0$ dan lingkaran B dengan persamaan $x^2+y^2+4x+2y-7=0$. Tentukan kedudukan dua lingkaran tersebut.
5. Diketahui dua lingkaran dengan persamaan $x^2+y^2+10x-2y-143=0$ dan $x^2+y^2-18x-2y-143=0$. Hitunglah jarak antara kedua titik potong lingkaran-lingkaran tersebut.

Semoga postingan: Lingkaran 6. Kedudukan Dua Lingkaran ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :