Logaritma 3. Persamaan Logaritma

Pada postingan sebelumnya kita sudah belajar materi Sifat-sifat Logaritma dan Fungsi Logaritma, pada postingan ini kita akan belajar mengenai Persamaan Logaritma.
Persamaan logaritma adalah persamaan dengan nilai variabel atau perubah tidak diketahui dalam logaritma.

A. Bentuk-bentuk Persamaan Logaritma

Berikut ini beberapa bentuk dari persamaan logaritma dan langkah-langkah penyelesaiannya:

1.	$^a\log f(x)={^a\log p}$ maka: solusi: $f(x)=p$ syarat: $f(x)>0$.
2.	$^a\log f(x)={^b\log f(x)}$ maka: solusi: $f(x)=1$ syarat: $f(x) > 0$.
3.	$^a\log f(x)={^a\log g(x)}$ maka: solusi: $f(x)=g(x)$ syarat: $f(x) > 0$ dan $g(x) > 0$
4.	$^{f(x)}\log g(x)={^{f(x)}\log h(x)}$ maka: solusi: $g(x)=h(x)$ syarat: (i) $f(x) > 0$ dan $f(x)\ne 1$ (ii) $g(x) > 0$ (iii) $h(x) > 0$.
5.	$^{f(x)}\log h(x)={^{g(x)}\log h(x)}$ maka: Solusi: $f(x)=g(x)$ dan $h(x)=1$ syarat: (i) $f(x) > 0$ dan $f(x)\ne 1$ (ii) $g(x) > 0$ dan $g(x)\ne 1$ (iii) $h(x) > 0$
6.	$a\left( ^m\log f(x) \right)^2+b\left( ^m\log f(x) \right)+c=0$ maka: solusi: Misalkan, $^m\log f(x)=p$ sehingga persamaan menjadi $a.p^2+b.p+c=0$, selanjutnya selesaikan menggunakan metode faktorisasi, rumus abc, atau metode melengkapkan kuadrat sempurna. syarat: $f(x) > 0$

Contoh 1.

Tentukan himpunan penyelesaian dari persamaan $^4\log (3x-1)=^4\log 5$.
Penyelesaian:
$\begin{align}^4\log (3x-1)=^4\log 5 \\ ^a\log f(x) &= ^4\log p \end{align}$
Solusi:
$\begin{align}f(x) &= p \\ 3x-1 &= 5 \\ 3x &= 6 \\ x &= 2 \end{align}$
syarat:

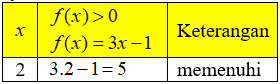
Jadi, HP = {2}

Contoh 2.

Tentukan himpunan penyelesaian dari persamaan $^4\log (x^2-7x+12)=\frac{1}{2}$
Penyelesaian:
$\begin{align}^4\log (x^2-7x+12) &= \frac{1}{2} \\ ^4\log (x^2-7x+12) &= ^4\log {4^{\frac{1}{2}}} \\ ^4\log (x^2-7x+12) &= ^4\log 2 \\ ^4\log f(x) &= ^4\log p \end{align}$
Solusi:
$\begin{align}f(x) &= p \\ x^2-7x+12 &= 2 \\ x^2-7x+10 &= 0 \\ (x-2)(x-5) &= 0 \end{align}$
$x-2=0\to x=2$
$x-5=0\to x=5$
Syarat:

Jadi, HP = {2, 5}

Contoh 3.

Tentukan himpunan penyelesaian dari persamaan $^2\log (2x-x^2)=^3\log (2x-x^2)$.
Penyelesaian:
$\begin{align}^2\log (2x-x^2) &= ^3\log (2x-x^2) \\ ^a\log f(x) &= ^b\log f(x) \end{align}$
Solusi:
$\begin{align}f(x) &= 1 \\ 2x-x^2 &= 1 \\ x^2-2x+1 &= 0 \\ (x-1)^2 &= 0 \\ x-1 &= 0 \\ x &= 1 \end{align}$
Syarat:

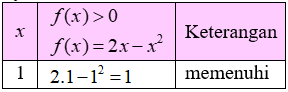
Jadi, HP = {1}

Contoh 4.

Tentukan himpunan penyelesaian dari $^7\log (x^2+13x+42)=^7\log (x+10)$.
Penyelesaian:
$\begin{align}^7\log (x^2+13x+42) &= ^7\log (x+10) \\ ^a\log f(x) &= ^a\log g(x) \end{align}$
Solusi:
$\begin{align}f(x) &= g(x) \\ x^2+13x+42 &= x+10 \\ x^2+12x+32 &= 0 \\ (x+8)(x+4) &= 0 \end{align}$
$x+8=0\to x=-8$
$x+4=0\to x=-4$
Syarat:

Jadi, HP = {-8, -4}

Contoh 5.

Tentukan himpunan penyelesaian dari $^{(x-3)}\log ({{x}^{2}}-6x+8){{=}^{(x-3)}}\log (2x-7)$.
Penyelesaian:
$\begin{align}^{(x-3)}\log (x^2-6x+8)&=^{(x-3)}\log (2x-7) \\ ^{f(x)}\log g(x) &= ^{f(x)}\log h(x) \end{align}$
Solusi: $g(x)=h(x)$ maka:
$\begin{align}x^2-6x+8 &= 2x-7 \\ x^2-8x+15 &= 0 \\ (x-3)(x-5) &= 0 \end{align}$
$x-3=0\to x=3$
$x-5=0\to x=5$
Syarat:

Jadi, HP = {5}

Contoh 6.

Tentukan himpunan penyelesaian dari $^{x^2-4}\log (3x-5)=^{10x-13}\log (3x-5)$.
Penyelesaian:
$\begin{align}^{x^2-4}\log (3x-5) &=^{10x-13}\log (3x-5) \\ ^{f(x)}\log h(x) &= ^{g(x)}\log h(x) \end{align}$
Solusi:
$\begin{align}f(x) &= g(x) \\ x^2-4 &= 10x-13 \\ x^2-10x+9 &= 0 \\ (x-1)(x-9) &= 0 \end{align}$
$x-1=0\to x=1$
$x-9=0\to x=9$
$\begin{align}h(x) &= 1 \\ 3x-5 &= 1 \\ 3x &= 6 \\ x &= 2 \end{align}$
Syarat:

Jadi, HP = {9}

Contoh 7.

Tentukan himpunan penyelesaian dari $^3\log^2x-3.^3\log x+2=0$.
Penyelesaian:
$^3\log^2x-3.^3\log x+2=0$
Syarat:
$\begin{align}f(x) & > 0 \\ x & > 0 \end{align}$
Solusi:
Misalkan, $^3\log x=p$ maka:
$\begin{align}^3\log^2x-3.^3\log x+2 &= 0 \\ \left( ^3\log x \right)^2-3.^3\log x+2 &= 0 \\ p^2-3p+2 &= 0 \\ (p-1)(p-2) &= 0 \end{align}$
$\begin{align}p-1 &= 0 \\ p &= 1 \\ ^3\log x &= 1 \\ x &= 3\,(\text{memenuhi}) \end{align}$
$\begin{align}p-2 &= 0 \\ p &= 2 \\ ^3\log x &= 2 \\ x &= 3^2 \\ x &= 9\,\,(\text{memenuhi}) \end{align}$
Jadi, HP = {3, 9}

Contoh 8.

Tentukan nilai $x$ yang memenuhi $^2\log^2(4x-4)-^2\log (4x-4)^4=^2\log \frac{1}{8}$.
Penyelesaian:
$^2\log^2(4x-4)-^2\log (4x-4)^4=^2\log \frac{1}{8}$
$({^2\log (4x-4)})^2-$$4.^2\log (4x-4)$$-^2\log 2^{-3}=0$
$\left( ^2\log (4x-4) \right)^2-4.^2\log (4x-4)+3=0$
Syarat:
$\begin{align}f(x) & > 0 \\ 4x-4 & > 0 \\ 4x & > 4 \\ x & > 1 \end{align}$
Misalkan, $^2\log (4x-4)=p$ maka:
$\left( ^2\log (4x-4) \right)^2-4.^2\log (4x-4)+3=0$
$p^2-4p+3=0$
$(p-1)(p-3)=0$
$\begin{align}p-1 &= 0 \\ p &= 1 \\ ^2\log (4x-4) &= 1 \\ 4x-4 &= 2^1 \\ 4x &= 6 \\ x &= \frac{6}{4} \\ x &= \frac{3}{2}\,(\text{memenuhi}) \end{align}$
$\begin{align}p-3 &= 0 \\ p &= 3 \\ ^2\log (4x-4) &= 3 \\ 4x-4 &= 2^3 \\ 4x &= 12 \\ x &= 3\,(\text{memenuhi}) \end{align}$
Jadi, HP = $\left\{ \frac{3}{2},\,3 \right\}$.

B. Sistem Persamaan Logaritma

Sistem persamaan logaritma adalah sekelompok persamaan logaritma yang mempunyai penyelesaian simultan.

Contoh 9.

Tentukan nilai $x$ yang memenuhi persamaan $2\log x-\log y=1$ dan $\log x+\log y=8$.
Penyelesaian:
$\begin{align}2\log x-\log y &= 1 \\ \log x+\log y &= 8 \end{align}$
-------------------------------- (+)
$\begin{align}3.\log x &= 9 \\ \log x &= 3 \\ x &= 10^3 \\ x &= 1.000 \end{align}$

Contoh 10.

Tentukan nilai $x$ yang memenuhi persamaan $\left( \begin{matrix} ^x\log a & \log (2a-2) \\ \log 4 & 1 \\ \end{matrix} \right) = \left( \begin{matrix} \frac{1}{2}b & 1 \\ \log b & 1 \\ \end{matrix} \right)$.
Penyelesaian:
$\left( \begin{matrix}2.^x\log a & \log (2a-2) \\ \log 4 & 1 \\ \end{matrix} \right)=\left( \begin{matrix} b & 1 \\ \log b & 1 \\ \end{matrix} \right)$
$\begin{align}\log (2a-2) &= 1 \\ \log (2a-2) &= \log 10 \\ 2a-2 &= 10 \\ 2a &= 12 \\ a &= 6 \end{align}$
$\log b=\log 4\to b=4$
$\begin{align}2.^x\log a &= b \\ 2.^x\log 6 &= 4 \\ ^x\log 6 &= 2 \\ x^2 &= 6 \\ x &= \sqrt{6} \end{align}$

C. Soal Latihan Persamaan Logaritma

1. Tentukan himpunan penyelesaian dari persamaan ${^2\log x}+{^2\log (x+2)}=3$.
2. Tentukan himpunan penyelesaian dari persamaan ${^5\log (x-1)}-{^5\log (x+3)}={^5\log (x+27)}$.
3. Tentukan nilai $x$ yang memenuhi persamaan $\left( ^4\log x \right)^2-{^2\log \sqrt{x}}-\frac{3}{4}=0$.
4. Diketahui $x$ memenuhi persamaan $^{(x-2)}\log (x^2+5)={^{(x-2)}\log (4x+10)}$ dan $a$ memenuhi $ax=7$. Tentukan nilai $a+x$.
5. Diketahui akar-akar persamaan $^2\log ^2x-6.^2\log x+8=0$ adalah $x_1$ dan $x_2$. Tentukan nilai $x_1+x_2$.

Semoga postingan: Logaritma 3. Persamaan Logaritma ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :