Barisan dan Deret Aritmetika

A. Definisi Barisan Aritmetika

Barisan $U_1$, $U_2$, $U_3$, …, $U_{n-1}$, $U_n$ disebut barisan aritmetika jika: $U_2-U_1=U_3-U_2=...=U_n-U_{n-1}=b$, dengan $b$ = beda dan $U_n$ = suku ke-n

---

Contoh:
Apabila tiga bilangan berurutan $(3x-3)$, $(3x-2)$, dan $(x^2+2x-1)$ merupakan tiga suku dari barisan aritmetika, tentukan nilai $x$ yang memenuhi.
Penyelesaian:
Barisan aritmetika:
$(3x-3)$, $(3x-2)$, $(x^2+2x-1)$, …
Syarat:
$\begin{align}U_2-U_1 &= U_3-U_2 \\ 2U_2 &= U_1+U_3 \\ 2(3x-2) &= 3x-3+x^2+2x-1 \\ 6x-4 &= x^2+5x-4 \\ 0 &= x^2-x \\ x(x-1) &= 0 \end{align}$
$x=0$atau $x-1=0\to x=1$

---

B. Suku ke-n Barisan Aritmetika

Berdasarkan definisi barisan aritmetika:
$U_2-U_1=U_3-U_2=...=U_n-U_{n-1}=b$
Misalkan:
$U_1=a$ maka:
$\begin{align}U_2-U_1 &= b \\ U_2 &= U_1+b \\ U_2 &= a+b \end{align}$
$\begin{align}U_2-U_1 &= b \\ U_2 &= U_1+b \\ U_2 &= a+b \end{align}$
Coba perhatikan polanya:
$U_1=a$
$U_2=a+b$
$U_3=a+2b$
…
$U_n=a+(n-1)b$

Jadi, rumus suku ke-n barisan aritmetika adalah:
$U_n=a+(n-1)b$
Dengan:
$\begin{align}a &= U_1 = \text{suku}\,\text{pertama} \\ b &= \text{beda} \\ U_n &= \text{suku}\,\text{ke-n} \\ n &= \text{banyak}\,\text{suku} \end{align}$

---

Contoh 1.
Tentukan rumus suku ke-n dari barisan bilangan 2, 5, 8, 11, …
Penyelesaian:
$a=2$
$\begin{align}b &= U_2-U_1 \\ &= 5-2 \\ b &= 3 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ &= 2+(n-1).3 \\ &= 2+3n-3 \\ U_n &= 3n-1 \end{align}$

---

Contoh 2.
Tentukan suku ke-25 dari barisan: 71, 67, 63, 61, …
Penyelesaian:
$a=71$
$\begin{align}b &= U_2-U_1 \\ &= 67-71 \\ b &= -4 \end{align}$
$\begin{align}U_n=a+(n-1)b \\ U_{25} &= a+24b \\ &= 71+24.(-4) \\ &= 71-96 \\ U_{25} &= -25 \end{align}$

---

Contoh 3.
Seorang ibu membagikan permen kepada 5 orang anaknya menurut aturan deret aritmetika. Semakin muda usia anak semakin banyak permen yang diperoleh. Jika banyak permen yang diterima anak kedua 11 buah dan anak keempat 19 buah, maka tentukan banyak permen yang diterima anak kelima.
Penyelesaian:
Misalkan:
$U_n$ = banyak permen anak ke-$n$
Barisan aritmetika: $U_n=a+(n-1)b$
Banyak permen anak kedua = 11 maka:
$\begin{align}U_2 &= 11 \\ a+b &= 11\,....\,(1) \end{align}$
Banyak permen anak keempat = 19 maka:
$\begin{align}U_4 &= 19 \\ a+3b &= 19\,....\,(2) \end{align}$
Dari persamaan (1) dan (2):
$\begin{align}a+b &= 11 \\ a+2b &= 19 \end{align}$
--------------------- (-)
$-b=-8\to b=8$
$\begin{align}a+b &= 11 \\ a+8 &= 11 \\ a &= 3 \end{align}$
Banyak permen anak kelima adalah:
$\begin{align}U_5 &= a+4b \\ &= 3+4.8 \\ U_5 &= 35 \end{align}$
Jadi, banyak permen anak kelima adalah 35.

---

Contoh 4.
Diketahui jumlah suku ketiga dan ketujuh dari barisan aritmetika adalah 34 dan suku kesepuluh adalah 32. Tentukan suku kelimabelas.
Penyelesaian:
Barisan aritmetika: $U_n=a+(n-1)b$
$\begin{align}U_3+U_7 &= 34 \\ (a+2b)+(a+6b) &= 34 \\ 2a+8b &= 34 \\ a+4b &= 17\,....\,(1) \end{align}$
$\begin{align}U_{10} &= 32 \\ a+9b &= 32\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$a+4b=17$
$a+9b=32$
----------------------- (-)
$-5b=-15\to b=3$
$\begin{align}a+4b &= 17 \\ a+4.3 &= 17 \\ a+12 &= 17 \\ a &= 5 \end{align}$
$\begin{align}U_{15} &= a+14b \\ &= 5+14.3 \\ U_{15} &= 47 \end{align}$
Jadi, suku kelimabelas barisan aritmetika tersebut adalah 47.

---

Contoh 5.
Sisi-sisi dari suatu segitiga siku-siku merupakan barisan aritmetika. Apabila kelilingnya adalah 36, tentukan luas segitiga tersebut.
Penyelesaian:
Cara 1.
Ketiga sisi segitiga:
$a$, $a+b$, $a+2b$
Keliling segitiga = 36 maka:
$\begin{align}a+(a+b)+(a+2b) &= 36 \\ 3a+3b &= 36 \\ a+b &= 12 \\ a &= 12-b \end{align}$
Karena segitiga siku-siku maka berlaku teorema pythagoras:
$\begin{align}(a+2b)^2 &= a^2+(a+b)^2 \\ (12-b+2b)^2 &= (12-b)^2+(12-b+b)^2 \\ (12+b)^2 &= (12-b)^2+12^2 \\ 144+24b+b^2 &= 144-24b+b^2+144 \\ 48b &= 144 \\ b &= 3 \end{align}$
$\begin{align}a &= 12-b \\ &= 12-3 \\ a &= 9 \end{align}$
Luas segitiga tersebut adalah:
$\begin{align}L &= \frac{1}{2}.a.(a+b) \\ &= \frac{1}{2}.9.(9+3) \\ L &= 54 \end{align}$

Cara 2. Alternatif

Jika panjang sisi-sisi dari suatu segitiga siku-siku membentuk barisan aritmetika maka ketiga sisinya adalah $3x$, $4x$, dan $5x$.

Keliling segitiga = 36 maka:
$\begin{align}3x+4x+5x &= 36 \\ 12x &= 36 \\ x &= 3 \end{align}$
Luas segitiga tersebut adalah:
$\begin{align}L &= \frac{1}{2}.3x.4x \\ &= \frac{1}{2}.(3.3).(4.3) \\ &= \frac{1}{2}.9.12 \\ L &= 54 \end{align}$
Jadi, luas segitiga tersebut adalah 54 satuan luas.

---

C. Suku Tengah Barisan Aritmetika

Barisan $U_1$, $U_2$, $U_3$, …, $U_n$ memiliki suku tengah jika banyak sukunya $n$ = ganjil, maka:
$U_t=\frac{a+U_n}{2}$ dan $t=\frac{n+1}{2}$
dengan:
$\begin{align}U_t &= \text{suku}\,\text{tengah} \\ a &= \text{suku}\,\text{pertama} \\ U_n &= \text{suku}\,\text{terakhir} \end{align}$

---

Contoh:
Barisan bilangan aritmetika terdiri dari 21 suku. Suku tengah barisan tersebut adalah 52, sedangkan $U_3+U_5+U_{15}=106$. suku ke-7 barisan tersebut adalah …
Penyelesaian:
Barisan aritmetika: $U_n=a+(n-1)b$
$n=21$ maka:
$\begin{align}t &= \frac{n+1}{2} \\ &= \frac{21+1}{2} \\ t &= 11 \end{align}$
$\begin{align}U_t &= 52 \\ U_{11} &= 52 \\ a+10b &= 52\,....\,(1) \end{align}$
$\begin{align}U_3+U_5+U_{15} &= 106 \\ a+2b+a+4b+a+14b &= 106 \\ 3a+20b &= 106\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\left. \begin{align}a+10b &= 52 \\ 3a+20b &= 106 \end{align} \right|\begin{matrix} \times 3 \\ \times 1 \\ \end{matrix}$
$\begin{align}3a+30b &= 156 \\ 3a+20b &= 106 \end{align}$
------------------------------ (-)
$10b=50\to b=5$
Substitusi ke persamaan (1):
$\begin{align}a+10b &= 52 \\ a+10.5 &= 52 \\ a+50 &= 52 \\ a &= 2 \end{align}$
$\begin{align}U_7 &= a+6b \\ &= 2+6.5 \\ U_7 &= 32 \end{align}$
Jadi, suku ketujuh barisan aritmetika tersebut adalah 32.

---

D. Suku Sisipan Barisan Aritmetika

• Jika di antara dua bilangan $x$ dan $y$ disisipkan $k$ buah bilangan sehingga membentuk barisan aritmetika dengan beda ($b$) adalah: $b=\frac{y-x}{k+1}$
• Jika di antara setiap dua suku pada suatu barisan aritmetika disisipkan sebanyak $k$ suku sehingga terbentuk barisan aritmetika baru dengan $a'=a$ dan $b'=\frac{b}{k+1}$. ($a'$ = suku pertama barisan aritmetika baru, $a$ = suku pertama barisan aritmetika awal, $b'$ = beda barisan aritmetika baru, dan $b$ = beda barisan aritmetika awal.

---

Contoh 1.
Di antara dua suku yang berurutan pada barisan 3, 18, 33, … disisipkan 4 buah bilangan sehingga membentuk barisan aritmetika yang baru. Tentukan suku kesembilan dari barisan aritmetika yang baru.

Penyelesaian: Lihat/Tutup

Barisan aritmetika lama:
3, 18, 33, …
$a=3$
$\begin{align}b &= U_2-U_1 \\ &= 18-3 \\ b &= 15 \end{align}$
Barisan aritmetika baru setelah disisipkan $k$ = 4 bilangan:
$a'=a=3$
$\begin{align}b' &= \frac{b}{k+1} \\ &= \frac{15}{4+1} \\ b' &= 3 \end{align}$
3, 6, 9, 12, 15, 18, …..
$\begin{align}U_9^{'} &= a'+(n-1)b' \\ &= 3+8.3 \\ U_9^{'} &= 27 \end{align}$

---

Contoh 2.
Di antara bilangan 21 dan 117 disisipkan 11 buah bilangan sehingga terbentuk barisan aritmetika. Tentukan beda dan suku ke-10 dari barisan aritmetika yang terbentuk.

Penyelesaian: Lihat/Tutup

$\underbrace{21}_{x},\underbrace{...,...,....,...}_{\text{disisip}\,\text{11}\,\text{bilangan}},\underbrace{117}_{y}$
$\begin{align}b &= \frac{y-x}{k+1} \\ &= \frac{117-21}{11+1} \\ b &= 8 \end{align}$
$a=21$
$\begin{align}U_n &= a+(n-1)b \\ U_{10} &= a+9b \\ &= 21+9.8 \\ U_{10} &= 93 \end{align}$

---

E. Deret Aritmetika

Deret aritmetika adalah jumlah semua suku-suku pada barisan aritmetika.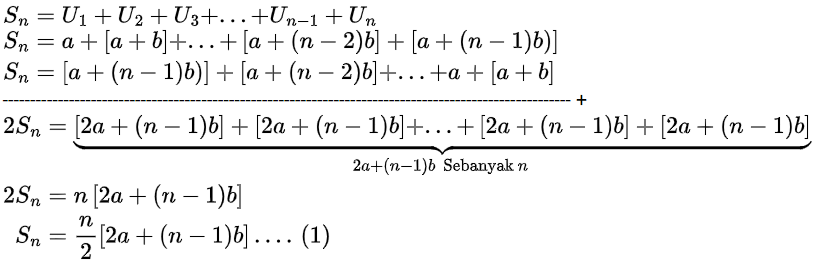

Dari rumus (1):
$\begin{align}S_n &= \frac{n}{2}\left[ 2a+(n-1)b \right] \\ &= \frac{n}{2}\left[ a+(a+(n-1)b) \right] \\ S_n &= \frac{n}{2}(a+U_n)\,....\,(2) \end{align}$

Dari rumus (2):
$\begin{align}S_n &= \frac{n}{2}(a+U_n) \\ &= n.\left( \frac{a+U_n}{2} \right) \\ S_n &= n.U_t\,....\,(3) \end{align}$

Perhatikan:
$U_1+U_2+U_3+...+U_{n-1}+U_n=S_n$
$U_1+U_2+U_3+...+U_{n-1}=S_{n-1}$
------------------------------------------------------------ (-)
$U_n=S_n-S_{n-1}\,....\,(4)$

Karena $U_1+U_2+U_3+...+U_{n-1}+U_n=S_n$ maka $U_1=S_1$

Berdasarkan penjelasan di atas maka kita peroleh beberapa rumus yang berkaitan dengan deret aritmetika yaitu:
$\begin{align}S_n &= \frac{n}{2}\left[ 2a+(n-1)b \right] \\ S_n &= \frac{n}{2}\left[ a+U_n \right] \\ S_n &= n.U_t \\ U_n &= S_n-S_{n-1} \\ U_1 &= S_1= a \end{align}$
dengan:
$\begin{align}S_n &= \text{jumlah}\,\text{n}\,\text{suku}\,\text{pertama} \\ U_n &= \,\text{suku}\,\text{ke-n} \\ U_t &= \text{suku}\,\text{tengah} \\ a &= U_1 = \text{suku}\,\text{pertama} \\ b &= \text{beda} \end{align}$

---

Contoh 1.
Tentukan jumlah 20 suku pertama dari barisan aritmetika: 60, 54, 48, 42, ….

Penyelesaian: Lihat/Tutup

$a=60$
$\begin{align}b &= U_2-U_1 \\ &= 54-60 \\ b &= -6 \end{align}$
$\begin{align}S_n &= \frac{n}{2}\left[ 2a+(n-1)b \right] \\ S_{20} &= \frac{20}{2}\left[ 2.60+19.(-6) \right] \\ &= 10(120-114) \\ S_{20} &= 60 \end{align}$
Jadi, jumlah 20 suku pertama barisan aritmetika tersebut adalah 60.

---

Contoh 2.
Tentukanlah jumlah deret aritmetika: 13 + 17 + 21 + … + 93 = ….

Penyelesaian: Lihat/Tutup

$a=13$
$\begin{align}b &= U_2-U_1 \\ &= 17-13 \\ b &= 4 \end{align}$
$\begin{align}U_n &= 93 \\ a+(n-1)b &= 93 \\ 13+(n-1).4 &= 93 \\ 13+4n-4 &= 93 \\ 4n &= 84 \\ n &= 21 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(a+U_n) \\ S_{21} &= \frac{21}{2}(13+93) \\ &= \frac{21}{2}.106 \\ S_{21} &= 1.113 \end{align}$

---

Contoh 3.
Jumlah $n$ suku pertama deret aritmetika ditentukan oleh $S_n=2n^2+n$. Jika $U_n$ menyatakan suku ke-$n$ deret tersebut maka $U_{12}$ adalah …

Penyelesaian: Lihat/Tutup

$\begin{align}U_n &= S_n-S_{n-1} \\ U_{12} &= S_{12}-S_{11} \\ &= \left( 2.12^2+12 \right)-\left( 2.11^2+11 \right) \\ &= 300-253 \\ U_{12} &= 47 \end{align}$

---

Contoh 4.
Dari deret Aritmatika diketahui suku tengah 32. Jika jumlah n suku pertama deret itu 672, tentukan banyak suku deret itu.

Penyelesaian: Lihat/Tutup

$U_t=32$ dan $S_n=672$ maka $n$ = …
$\begin{align}S_n &= n.U_t \\ 672 &= n.32 \\ n &= 21 \end{align}$
Jadi, banyak suku deret itu adalah 21.

---

Contoh 5.
Jumlah bilangan-bilangan bulat antara 250 dan 1.000 yang habis dibagi 7 adalah …

Penyelesaian: Lihat/Tutup

$\left\lceil x \right\rceil $ = bilangan bulat terkecil yang lebih dari sama dengan $x$ (pembulatan ke atas).
$\left\lfloor x \right\rfloor $ = bilangan bulat terbesar yang kurang dari sama dengan $x$ (pembulatan ke bawah).
$\begin{align}\left\lceil \frac{250}{7} \right\rceil \times 7 &= \left\lceil 35,71 \right\rceil \times 7 \\ &= 36\times 7 \\ &= 252 \end{align}$
dan
$\begin{align}\left\lfloor \frac{1.000}{7} \right\rfloor \times 7 &= \left\lfloor 142,86 \right\rfloor \times 7 \\ &= 142\times 7 \\ &= 994 \end{align}$
Bilangan-bilangan bulat antara 250 dan 1.000 yang habis dibagi 7 adalah:
252, 259, 266, …., 994
$a=252$, $b=7$
$\begin{align}U_n &= 994 \\ a+(n-1)b &= 994 \\ 252+(n-1)7 &= 994 \\ 252+7n-7 &= 994 \\ 7n &= 749 \\ n &= 107 \end{align}$
Jumlah bilangan-bilangan tersebut adalah:
$\begin{align}S_n &= \frac{n}{2}\left( a+U_n \right) \\ S_{107} &= \frac{107}{2}\left( 252+994 \right) \\ &= 66.661 \end{align}$

---

F. Soal Latihan

1. Suku keempat dan suku ketujuh suatu barisan aritmetika berturut–turut adalah 5 dan 14. Tentukan suku kelima belas barisan tersebut.
2. Antara bilangan 20 dan 116 disisipkan 16 bilangan. Bilangan itu bersama bilangan semula membentuk sebuah barisan aritmetika. Tentukan jumlah semua suku barisan tersebut.
3. Suku ke tujuh dan suku ke dua barisan artimatika berturut–turut adalah 43 dan 13. Tentukan jumlah sepuluh suku pertama deret aritmatika itu.
4. Jumlah n suku pertama deret aritmatika dinyatakan dengan ${{S}_{n}}={{n}^{2}}-5n$. Tentukan suku ke-20 dari deret aritmetika tersebut.
5. Tempat duduk pertunjukan film di atur mulai dari depan ke belakang dengan banyak baris di belakang lebih 4 kursi dari baris di depannya. Bila dalam gedung pertunjukan terdapat 15 baris terdepan ada 20 kursi, maka tentukan kapasitas gedung pertunjukan tersebut.

Untuk lebih memantapkan pemahaman mengenai barisan dan deret aritmetika silahkan belajar mandiri melalui Kumpulan Soal Barisan dan Deret Aritmetika

Semoga postingan: Barisan dan Deret Aritmetika ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :