Soal Trigonometri Jumlah dan Selisih Dua Sudut dan Pembahasan

Hallo...! Pengunjung setia Catatan Matematika, kali ini Bang RP (Reikson Panjaitan, S.Pd) berbagi Kumpulan Soal Trigonometri Jumlah/Selisih Dua Sudut berserta pembahasannya. Ayo... manfaatkan website Catatan Matematika ini untuk belajar matematika secara online.

Tata Cara Belajar:
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cek jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".

---

Soal No. 1

Perhatikan pernyataan berikut.
1) $\sin (x+y)=\sin x\cos y+\cos x\sin y$
2) $\sin (x-y)=\sin x\cos y+\cos x\sin y$
3) $\cos (x+y)=\cos x\cos y+\sin x\sin y$
4) $\cos (x-y)=\cos x\cos y+\sin x\sin y$
5) $\tan (x+y)=\frac{\tan x+\tan y}{1-\tan x\tan y}$
6) $\tan (x-y)=\frac{\tan x+\tan y}{1+\tan x\tan y}$
Pernyataan yang benar adalah …
A. 1), 3), dan 5)
B. 1), 4), dan 5)
C. 1), 4), dan 6)
D. 2), 3), dan 6)
E. 2), 4), dan 6)

Penyelesaian: Lihat/Tutup

Cukup jelas
Jawaban: B

Soal No. 2

Perhatikan segitiga ABC berikut.

Nilai $\sin (x-y)$ = ….
A. $-\frac{96}{100}$
B. $-\frac{28}{100}$
C. 0
D. $\frac{28}{100}$
E. $\frac{96}{100}$

Penyelesaian: Lihat/Tutup

$\begin{align}AC &= \sqrt{BC^2-AB^2} \\ &= \sqrt{10^2-6^2} \\ &= \sqrt{100-36} \\ &= \sqrt{64} \\ AC &= 8 \end{align}$
$\sin x=\frac{AB}{BC}=\frac{6}{10}$ dan $\cos x=\frac{AC}{BC}=\frac{8}{10}$
$\sin y=\frac{AC}{BC}=\frac{8}{10}$ dan $\cos y=\frac{AB}{BC}=\frac{6}{10}$
$\begin{align}\sin (x-y) &= \sin x\cos y-\cos x\sin y \\ &= \frac{6}{10}\times \frac{6}{10}-\frac{8}{10}\times \frac{8}{10} \\ &= \frac{36}{100}-\frac{64}{100} \\ \sin (x-y) &= -\frac{28}{100} \end{align}$
Jawaban: B

Soal No. 3

Nilai $\cos 15^\circ $ adalah ….
A. $\frac{1}{4}(\sqrt{6}+\sqrt{2})$
B. $\frac{1}{4}(\sqrt{6}-\sqrt{2})$
C. $\frac{1}{4}(\sqrt{2}-\sqrt{6})$
D. $\frac{1}{2}(\sqrt{3}-\sqrt{2})$
E. $\frac{1}{2}(\sqrt{3}+\sqrt{2})$

Penyelesaian: Lihat/Tutup

$\begin{align}\cos 15^\circ &= \cos (45^\circ -30^\circ ) \\ &= \cos 45^\circ \cos 30^\circ +\sin 45^\circ \sin 30^\circ \\ &= \frac{1}{2}\sqrt{2}\times \frac{1}{2}\sqrt{3}+\frac{1}{2}\sqrt{2}\times \frac{1}{2} \\ &= \frac{1}{4}\sqrt{6}+\frac{1}{4}\sqrt{2} \\ \cos 15^\circ &= \frac{1}{4}(\sqrt{6}+\sqrt{2}) \end{align}$
Jawaban: A

Soal No. 4

Nilai $\tan 105^\circ $ adalah ….
A. $-2-2\sqrt{3}$
B. $-2-\sqrt{3}$
C. $-2+\sqrt{3}$
D. $-2+2\sqrt{3}$
E. $2+2\sqrt{3}$

Penyelesaian: Lihat/Tutup

$\begin{align}\tan 105^\circ &= \tan (60+45) \\ &= \frac{\tan 45^\circ +\tan 60^\circ }{1-\tan 45^\circ \tan 60^\circ } \\ &= \frac{1+\sqrt{3}}{1-1\times \sqrt{3}} \\ &= \frac{1+\sqrt{3}}{1-\sqrt{3}}\times \frac{1+\sqrt{3}}{1+\sqrt{3}} \\ &= \frac{1+2\sqrt{3}+3}{1-3} \\ &= \frac{4+2\sqrt{3}}{-2} \\ \tan 105^\circ &= -2-\sqrt{3} \end{align}$
Jawaban: B

Soal No. 5

Diketahui $0^\circ \le x\le 90^\circ $ dan $\tan x=\frac{4}{3}$. Nilai $\sin (30^\circ -x)$ adalah ….
A. $\frac{1}{10}(4\sqrt{3}-3)$
B. $\frac{1}{10}(4\sqrt{3}+3)$
C. $\frac{1}{10}(3-4\sqrt{3})$
D. $\frac{1}{10}(3-2\sqrt{3})$
E. $\frac{1}{10}(2\sqrt{3}+3)$

Penyelesaian: Lihat/Tutup

$\tan x=\frac{4}{3}=\frac{de}{sa}$ maka:
$\begin{align}mi &= \sqrt{de^2+sa^2} \\ &= \sqrt{4^2+3^2} \\ mi &= 5 \end{align}$
$\sin x=\frac{de}{mi}=\frac{4}{5}$ dan $\cos x=\frac{sa}{mi}=\frac{3}{5}$
$\begin{align}\sin (30^\circ -x) &= \sin 30^\circ \cos x-\cos 30^\circ \sin x \\ &= \frac{1}{2}\times \frac{3}{5}-\frac{1}{2}\sqrt{3}\times \frac{4}{5} \\ &= \frac{3}{10}-\frac{4\sqrt{3}}{10} \\ \sin (30^\circ -x) &= \frac{1}{10}(3-4\sqrt{3}) \end{align}$
Jawaban: C

Soal No. 6

Bentuk sederhana dari $\sin \alpha -\sin (\alpha -120^\circ )-\sin (\alpha -240^\circ )$ adalah ….
A. $\sin \alpha $
B. $\cos \alpha $
C. $\sin 2\alpha $
D. $2\sin \alpha $
E. $2\cos \alpha $

Penyelesaian: Lihat/Tutup

$\sin \alpha -\sin (\alpha -120^\circ )-\sin (\alpha -240^\circ )$
= $\sin \alpha-$$(\sin \alpha \cos 120^\circ -\cos \alpha \sin 120^\circ )-$$(\sin \alpha \cos 240^\circ -\cos \alpha \sin 240^\circ )$
= $\sin \alpha-$$(\sin \alpha .(-\frac{1}{2})-\cos \alpha .\frac{1}{2}\sqrt{3})-$$(\sin \alpha .\frac{1}{2}-\cos \alpha .(-\frac{1}{2}\sqrt{3}))$
= $\sin \alpha+$$\frac{1}{2}\sin \alpha$ + $\frac{1}{2}\sqrt{3}\cos \alpha-$ $\frac{1}{2}\sin \alpha-$ $\frac{1}{2}\sqrt{3}\cos \alpha $
= $\sin \alpha $
Jawaban: A

Soal No. 7

Diketahui $\sin x=\frac{3}{5}$ dan $\cos y=\frac{12}{13}$, $x$ sudut tumpul dan $y$ sudut lancip. Nilai $\tan (x+y)$ adalah .…
A. $-\frac{56}{33}$
B. $-\frac{16}{63}$
C. $\frac{8}{63}$
D. $\frac{16}{63}$
E. $\frac{56}{33}$

Penyelesaian: Lihat/Tutup

$\sin x=\frac{3}{5}=\frac{de}{mi}$; $x$ sudut tumpul maka:
$\begin{align}\tan x &= -\frac{de}{sa} \\ &= -\frac{de}{\sqrt{mi^2-de^2}} \\ &= -\frac{3}{\sqrt{5^2-3^2}} \\ \tan x &= -\frac{3}{4} \end{align}$
$\cos y=\frac{12}{13}=\frac{sa}{mi}$; $y$ sudut lancip maka:
$\begin{align}\tan y &= \frac{de}{sa} \\ &= \frac{\sqrt{mi^2-sa^2}}{sa} \\ &= \frac{\sqrt{13^2-12^2}}{12} \\ \tan y &= \frac{5}{12} \end{align}$
$\begin{align}\tan (x+y) &= \frac{\tan x+\tan y}{1-\tan x\tan y} \\ &= \frac{-\frac{3}{4}+\frac{5}{12}}{1-\left( -\frac{3}{4} \right)\times \frac{5}{12}} \\ &= \frac{-\frac{4}{12}}{1+\frac{5}{16}} \\ &= \frac{-\frac{1}{3}}{\frac{21}{16}} \\ &= -\frac{1}{3}\times \frac{16}{21} \\ \tan (x+y) &= -\frac{16}{63} \end{align}$
Jawaban: B

Soal No. 8

Jika $A+B=\frac{\pi }{3}$ dan $\cos A\cos B=\frac{7}{12}$, nilai $\cos (A-B)$ adalah ….
A. $\frac{1}{4}$
B. $\frac{1}{2}$
C. $\frac{3}{4}$
D. 1
E. $\frac{5}{4}$

Penyelesaian: Lihat/Tutup

$\begin{align}A+B &= \frac{\pi }{3} \\ \cos (A+B) &= \cos \frac{\pi }{3} \\ \cos A\cos B-\sin A\sin B &= \frac{1}{2} \\ \frac{7}{12}-\sin A\sin B &= \frac{1}{2} \\ -\sin A\sin B &= \frac{1}{2}-\frac{7}{12} \\ -\sin A\sin B &= -\frac{1}{12} \\ \sin A\sin B &= \frac{1}{12} \end{align}$
$\begin{align}\cos (A-B) &= \cos A\cos B+\sin A\sin B \\ &= \frac{7}{12}-\frac{1}{12} \\ &= \frac{6}{12} \\ \cos (A-B) &= \frac{1}{2} \end{align}$
Jawaban: B

Soal No. 9

Jika $\tan A=\frac{4}{3}$ dan $\tan B=7$, hasil $A+B$ adalah ….
A. $45^\circ $
B. $135^\circ $
C. $150^\circ $
D. $225^\circ $
E. $330^\circ $

Penyelesaian: Lihat/Tutup

$\begin{align}\tan (A+B) &= \frac{\tan A+\tan B}{1-\tan A\tan B} \\ &= \frac{\frac{4}{3}+7}{1-\frac{4}{3}\times 7} \\ &= \frac{\frac{25}{3}}{1-\frac{28}{3}} \\ &= \frac{\frac{25}{3}}{\frac{-25}{3}} \\ \tan (A+B) &= -1 \\ A+B &= {{\tan }^{-1}}(-1) \\ A+B &= 135^\circ \end{align}$
Jawaban: B

Soal No. 10

Jika $a\sin x+b\cos x=\sin (30^\circ +x)$ untuk setiap $x$, maka $a\sqrt{3}+b$ = …
A. $-1$
B. $-2$
C. 1
D. 2
E. 3

Penyelesaian: Lihat/Tutup

$\begin{align}a\sin x+b\cos x &= \sin (30^\circ +x) \\ &= \sin 30^\circ \cos x+\cos 30^\circ \sin x \\ &= \frac{1}{2}\cos x+\frac{1}{2}\sqrt{3}\sin x \\ a\sin x+b\cos x &= \frac{1}{2}\sqrt{3}\sin x+\frac{1}{2}\cos x \end{align}$
$a=\frac{1}{2}\sqrt{3}$ dan $b=\frac{1}{2}$ maka:
$a\sqrt{3}+b=\frac{1}{2}\sqrt{3}.\sqrt{3}+\frac{1}{2}=2$
Jawaban: D

Soal No. 11

Diketahui $\tan \alpha -\tan \beta =\frac{1}{3}$ dan $\cos \alpha \cos \beta =\frac{48}{65}$, ($\alpha $, $\beta $ lancip). Nilai $\sin (\alpha -\beta )$ = ….
A. $\frac{63}{65}$
B. $\frac{33}{65}$
C. $\frac{30}{65}$
D. $\frac{26}{65}$
E. $\frac{16}{65}$

Penyelesaian: Lihat/Tutup

$\begin{align}\tan \alpha -\tan \beta &= \frac{1}{3} \\ \frac{\sin \alpha }{\cos \alpha }-\frac{\sin \beta }{\cos \beta } &= \frac{1}{3} \\ \frac{\sin \alpha \cos \beta -\cos \alpha \sin \beta }{\cos \alpha \cos \beta } &= \frac{1}{3} \\ \frac{\sin (\alpha -\beta )}{\frac{48}{65}} &= \frac{1}{3} \\ \sin (\alpha -\beta ) &= \frac{1}{3}\times \frac{48}{65} \\ \sin (\alpha -\beta ) &= \frac{16}{65} \end{align}$
Jawaban: E

Soal No. 12

Diketahui $\tan \alpha =\frac{3}{4}$ dan $\tan \beta =\frac{5}{12}$; $\alpha $ dan $\beta $ sudut lancip, maka nilai $\cos (\alpha +\beta )$ = ….
A. $\frac{64}{65}$
B. $\frac{63}{65}$
C. $\frac{36}{65}$
D. $\frac{33}{65}$
E. $\frac{30}{65}$

Penyelesaian: Lihat/Tutup

$\alpha $ sudut lancip maka $\sin \alpha $ (positif) dan $\cos \alpha $ (positif).
$\tan \alpha =\frac{3}{4}=\frac{de}{sa}$
$\begin{align}mi &= \sqrt{de^2+sa^2} \\ &= \sqrt{3^2+4^2} \\ mi &= 5 \end{align}$
$\sin \alpha =\frac{de}{mi}\Leftrightarrow \sin \alpha =\frac{3}{5}$
$\cos \alpha =\frac{sa}{mi}\Leftrightarrow \cos \alpha =\frac{4}{5}$
$\beta $ sudut lancip maka $\sin \beta $ (positif) dan $\cos \beta $ (positif).
$\tan \beta =\frac{5}{12}=\frac{de}{sa}$
$\begin{align}mi &= \sqrt{de^2+sa^2} \\ &= \sqrt{5^2+12^2} \\ mi &= 13 \end{align}$
$\sin \beta =\frac{de}{mi}\Leftrightarrow \sin \beta =\frac{5}{13}$
$\cos \beta =\frac{sa}{mi}\Leftrightarrow \cos \beta =\frac{12}{13}$
$\begin{align}\cos (\alpha +\beta ) &= \cos \alpha \cos \beta -\sin \alpha \sin \beta \\ &= \frac{4}{5}\times \frac{12}{13}-\frac{3}{5}\times \frac{5}{13} \\ &= \frac{48}{65}-\frac{15}{65} \\ \cos (\alpha +\beta ) &= \frac{33}{65} \end{align}$
Jawaban: D

Soal No. 13

Diketahui $(A+B)=\frac{\pi }{3}$ dan $\sin A\sin B=\frac{1}{4}$. Nilai dari $\cos (A-B)$ = …
A. $-1$
B. $-\frac{1}{2}$
C. $\frac{1}{2}$
D. $\frac{3}{4}$
E. 1

Penyelesaian: Lihat/Tutup

$\begin{align}(A+B) &= \frac{\pi }{3} \\ \cos (A+B) &= \cos \frac{\pi }{3} \\ \cos A\cos B-\sin A\sin B &= \frac{1}{2} \\ \cos A\cos B-\frac{1}{4} &= \frac{1}{2} \\ \cos A\cos B &= \frac{1}{2}+\frac{1}{4} \\ \cos A\cos B &= \frac{3}{4} \end{align}$
$\begin{align}\cos (A-B) &= \cos A\cos B+\sin A\sin B \\ &= \frac{3}{4}+\frac{1}{4} \\ \cos (A-B) &= 1 \end{align}$
Jawaban: E

Soal No. 14

Diketahui $\sin A=\frac{4}{5}$ dan $\sin B=\frac{7}{25}$ dengan A sudut lancip dan B sudut tumpul. Nilai $\cos (A-B)$ = ….
A. $-\frac{117}{125}$
B. $-\frac{100}{125}$
C. $-\frac{75}{125}$
D. $-\frac{44}{125}$
E. $-\frac{21}{125}$

Penyelesaian: Lihat/Tutup

A sudut lancip maka $\cos A$ (positif).
$\sin A=\frac{4}{5}=\frac{de}{mi}$
$\begin{align}sa &= \sqrt{mi^2-de^2} \\ &= \sqrt{5^2-4^2} \\ sa &= 3 \end{align}$
$\cos A=\frac{sa}{mi}\Leftrightarrow \cos A=\frac{3}{5}$
B sudut tumpul maka $\cos B$ (negatif).
$\sin B=\frac{7}{25}=\frac{de}{mi}$
$\begin{align}sa &= \sqrt{mi^2-de^2} \\ &= \sqrt{25^2-7^2} \\ sa &= 24 \end{align}$
$\cos B=-\frac{sa}{mi}\Leftrightarrow \cos B=-\frac{24}{25}$
$\begin{align}\cos (A-B) &= \cos A\cos B+\sin A\sin B \\ &= \frac{3}{5}\times \left( -\frac{24}{25} \right)+\frac{4}{5}\times \frac{7}{25} \\ &= \frac{-72}{125}+\frac{28}{125} \\ \cos (A-B) &= -\frac{44}{125} \end{align}$
Jawaban: D

Soal No. 15

Diketahui $\cos \alpha =\frac{3}{5}$, $\alpha $ adalah sudut lancip dan $\sin \beta =\frac{12}{13}$, $\beta $ adalah sudut tumpul, maka nilai $\tan (\alpha +\beta )$ = ….
A. $\frac{63}{16}$
B. $\frac{56}{63}$
C. $\frac{16}{63}$
D. $-\frac{16}{63}$
E. $-\frac{56}{63}$

Penyelesaian: Lihat/Tutup

$\alpha $ adalah sudut lancip maka $\tan \alpha $ positif.
$\cos \alpha =\frac{3}{5}=\frac{sa}{mi}$
$\begin{align}de &= \sqrt{mi^2-sa^2} \\ &= \sqrt{5^2-3^2} \\ de &= 4 \end{align}$
$\tan \alpha =\frac{de}{sa}\Leftrightarrow \tan \alpha =\frac{4}{3}$
$\beta $ adalah sudut tumpul maka $\tan \beta $ negatif.
$\sin \beta =\frac{12}{13}=\frac{de}{mi}$
$\begin{align}sa &= \sqrt{mi^2-de^2} \\ &= \sqrt{13^2-12^2} \\ sa &= 5 \end{align}$
$\tan \beta =-\frac{de}{sa}\Leftrightarrow \tan \beta =-\frac{12}{5}$
$\begin{align}\tan (\alpha +\beta ) &= \frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta } \\ &= \frac{\frac{4}{3}+\left( -\frac{12}{5} \right)}{1-\frac{4}{3}\left( -\frac{12}{5} \right)} \\ &= \frac{\frac{20}{15}-\frac{36}{15}}{1+\frac{48}{15}} \\ &= \frac{-\frac{16}{15}}{\frac{63}{15}} \\ \tan (\alpha +\beta ) &= -\frac{16}{63} \end{align}$
Jawaban: D

Soal No. 16

Diketahui $\sin \beta =\frac{12}{13}$, $\beta $ adalah sudut lancip dan $\sin \alpha =\frac{3}{5}$, $\alpha $ adalah sudut tumpul, maka nilai $\tan (\alpha -\beta )$ = ….
A. $-\frac{63}{16}$
B. $-\frac{63}{56}$
C. $\frac{16}{63}$
D. $\frac{56}{63}$
E. $\frac{63}{16}$

Penyelesaian: Lihat/Tutup

$\beta $ adalah sudut lancip maka $\tan \beta $ positif.
$\sin \beta =\frac{12}{13}=\frac{de}{mi}$
$\begin{align}sa &= \sqrt{mi^2-de^2} \\ &= \sqrt{13^2-12^2} \\ sa &= 5 \end{align}$
$\tan \beta =\frac{de}{sa}\Leftrightarrow \tan \beta =\frac{12}{5}$
$\alpha $ adalah sudut tumpul maka $\tan \alpha $ negatif.
$\sin \alpha =\frac{3}{5}=\frac{de}{mi}$
$\begin{align}sa &= \sqrt{mi^2-de^2} \\ &= \sqrt{5^2-3^2} \\ sa &= 4 \end{align}$
$\tan \alpha =-\frac{de}{sa}\Leftrightarrow \tan \alpha =-\frac{3}{4}$
$\begin{align}\tan (\alpha -\beta ) &= \frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta } \\ &= \frac{-\frac{3}{4}-\frac{12}{5}}{1+\left( -\frac{3}{4} \right).\frac{12}{5}} \\ &= \frac{-\frac{15}{20}-\frac{48}{20}}{1-\frac{36}{20}} \\ &= \frac{-\frac{63}{20}}{-\frac{16}{20}} \\ \tan (\alpha -\beta ) &= \frac{63}{16} \end{align}$
Jawaban: E

Soal No. 17

Diketahui $p$ dan $q$ adalah sudut lancip dan $p-q=30^\circ $. Jika $\cos p\sin q=\frac{1}{6}$, maka nilai dari $\sin p\cos q$ = ….
A. $\frac{1}{6}$
B. $\frac{2}{6}$
C. $\frac{3}{6}$
D. $\frac{4}{6}$
E. $\frac{5}{6}$

Penyelesaian: Lihat/Tutup

$\begin{align}p-q &= 30^\circ \\ \sin (p-q) &= \sin 30^\circ \\ \sin p\cos q-\cos p\sin q &= \frac{1}{2} \\ \sin p\cos q-\frac{1}{6} &= \frac{1}{2} \\ \sin p\cos q &= \frac{1}{2}+\frac{1}{6} \\ \sin p\cos q &= \frac{3}{6}+\frac{1}{6} \\ \sin p\cos q &= \frac{4}{6} \end{align}$
Jawaban: D

Soal No. 18

Pada segitiga ABC lancip, diketahui $\cos A=\frac{4}{5}$ dan $\sin B=\frac{12}{13}$, maka $\sin C$ = ….
A. $\frac{20}{65}$
B. $\frac{36}{65}$
C. $\frac{56}{65}$
D. $\frac{60}{65}$
E. $\frac{63}{65}$

Penyelesaian: Lihat/Tutup

$\cos A=\frac{4}{5}=\frac{sa}{mi}$
$\begin{align}de &= \sqrt{mi^2-sa^2} \\ &= \sqrt{5^2-4^2} \\ de &= 3 \end{align}$
$\sin A=\frac{de}{mi}\Leftrightarrow \sin A=\frac{3}{5}$
$\sin B=\frac{12}{13}=\frac{de}{mi}$
$\begin{align}sa &= \sqrt{mi^2-de^2} \\ &= \sqrt{13^2-12^2} \\ sa &= 5 \end{align}$
$\cos B=\frac{sa}{mi}\Leftrightarrow \cos B=\frac{5}{13}$
Segitiga ABC maka:
$\begin{align}A+B+C &= 180^\circ \\ C &= 180^\circ -(A+B) \\ \sin C &= \sin (180^\circ -(A+B)) \\ &= \sin (A+B) \\ &= \sin A\cos B+\cos A\sin B \\ &= \frac{3}{5}.\frac{5}{13}+\frac{4}{5}.\frac{12}{13} \\ &= \frac{15}{65}+\frac{48}{65} \\ \sin C &= \frac{63}{65} \end{align}$
Jawaban: E

Soal No. 19

Pada segitiga PQR diketahui $\sin P=\frac{3}{5}$ dan $\cos Q=\frac{12}{13}$ maka nilai $\sin R$ = ….
A. $\frac{56}{65}$
B. $\frac{16}{65}$
C. $-\frac{6}{65}$
D. $-\frac{16}{65}$
E. $-\frac{56}{65}$

Penyelesaian: Lihat/Tutup

$\sin P=\frac{3}{5}=\frac{de}{mi}$
$\begin{align}sa &= \sqrt{mi^2-de^2} \\ &= \sqrt{5^2-3^2} \\ sa &= 4 \end{align}$
$\cos P=\frac{sa}{mi}\Leftrightarrow \cos P=\frac{4}{5}$
$\cos Q=\frac{12}{13}=\frac{sa}{mi}$
$\begin{align}de &= \sqrt{mi^2-sa^2} \\ &= \sqrt{13^2-12^2} \\ de &= 5 \end{align}$
$\sin Q=\frac{de}{mi}\Leftrightarrow \sin Q=\frac{5}{13}$
Segitiga PQR maka:
$\begin{align}P+Q+R &= 180^\circ \\ R &= 180^\circ -(P+Q) \\ \sin R &= \sin (180^\circ -(P+Q)) \\ &= \sin (P+Q) \\ &= \sin P\cos Q+\cos P\sin Q \\ &= \frac{3}{5}.\frac{12}{13}+\frac{4}{5}.\frac{5}{13} \\ &= \frac{36}{65}+\frac{20}{65} \\ \sin R &= \frac{56}{65} \end{align}$
Jawaban: A

Soal No. 20

Dari suatu segitiga ABC diketahui bahwa $\sin A=\frac{1}{2}\sqrt{2}$ dan $\cos B=\frac{1}{2}$. Nilai $\sin C$ adalah ….
A. $\frac{1}{4}\sqrt{2}$
B. $\frac{1}{4}\sqrt{6}$
C. $\frac{1}{4}\sqrt{2}+\sqrt{6}$
D. $\frac{1}{4}(\sqrt{2}+\sqrt{6})$
E. $\frac{1}{4}\sqrt{12}$

Penyelesaian: Lihat/Tutup

$\sin A=\frac{\sqrt{2}}{2}=\frac{de}{mi}$
$\begin{align}sa &= \sqrt{mi^2-de^2} \\ &= \sqrt{2^2-(\sqrt{2})^2} \\ sa &= \sqrt{2} \end{align}$
$\cos A=\frac{sa}{mi}\Leftrightarrow \cos A=\frac{\sqrt{2}}{2}$
$\cos B=\frac{1}{2}=\frac{sa}{mi}$
$\begin{align}de &= \sqrt{mi^2-sa^2} \\ &= \sqrt{2^2-1^2} \\ de &= \sqrt{3} \end{align}$
$\sin B=\frac{de}{mi}\Leftrightarrow \sin B=\frac{\sqrt{3}}{2}$
Segitiga ABC maka:
$\begin{align}A+B+C &= 180^\circ \\ C &= 180^\circ -(A+B) \\ \sin C &= \sin (180^\circ -(A+B)) \\ &= sin(A+B) \\ &= sinAcosB+cosAsinB \\ &= \frac{\sqrt{2}}{2}.\frac{1}{2}+\frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2} \\ &= \frac{\sqrt{2}}{4}+\frac{\sqrt{6}}{4} \\ \sin C &= \frac{1}{4}(\sqrt{2}+\sqrt{6}) \end{align}$
Jawaban: D

Soal No. 21

Dari suatu segitiga ABC diketahui bahwa $\sin A=\frac{1}{2}\sqrt{3}$ dan $\cos B=\frac{1}{2}\sqrt{2}$. Nilai $\sin C$ adalah ….
A. $\frac{1}{4}\sqrt{2}$
B. $\frac{1}{4}\sqrt{6}$
C. $\frac{1}{4}(\sqrt{2}+\sqrt{6})$
D. $\frac{1}{4}\sqrt{2}+\sqrt{6}$
E. $\frac{1}{4}\sqrt{12}$

Penyelesaian: Lihat/Tutup

$\sin A=\frac{\sqrt{3}}{2}=\frac{de}{mi}$
$\begin{align}sa &= \sqrt{mi^2-de^2} \\ &= \sqrt{2^2-(\sqrt{3})^2} \\ sa &= 1 \end{align}$
$\cos A=\frac{sa}{mi}\Leftrightarrow \cos A=\frac{1}{2}$
$\cos B=\frac{\sqrt{2}}{2}=\frac{sa}{mi}$
$\begin{align}de &= \sqrt{mi^2-sa^2} \\ &= \sqrt{2^2-(\sqrt{2})^2} \\ de &= \sqrt{2} \end{align}$
$\sin B=\frac{de}{mi}\Leftrightarrow \sin B=\frac{\sqrt{2}}{2}$
$\begin{align}A+B+C &= 180^\circ \\ C &= 180^\circ -(A+B) \\ \sin C &= \sin (180^\circ -(A+B)) \\ &= \sin (A+B) \\ &= \sin A\cos B+\cos A\sin B \\ &= \frac{\sqrt{3}}{2}.\frac{\sqrt{2}}{2}+\frac{1}{2}.\frac{\sqrt{2}}{2} \\ &= \frac{\sqrt{6}}{4}+\frac{\sqrt{2}}{4} \\ \sin C &= \frac{1}{4}(\sqrt{6}+\sqrt{2}) \end{align}$
Jawaban: C

Soal No. 22

Nilai $\sin 48^\circ \cos 12^\circ +\cos 48^\circ \sin 12^\circ $ sama dengan ….
A. $\frac{1}{2}$
B. $\frac{1}{2}\sqrt{2}$
C. $\frac{1}{2}\sqrt{3}$
D. $\frac{1}{2}\sqrt{6}$
E. $\frac{1}{3}\sqrt{3}$

Penyelesaian: Lihat/Tutup

$\sin 48^\circ \cos 12^\circ +\cos 48^\circ \sin 12^\circ $
= $\sin (48^\circ +12^\circ )$
= $\sin 60^\circ $
= $\frac{1}{2}\sqrt{3}$
Jawaban: C

Soal No. 23

Jika $\cot 49^\circ =\frac{1}{a}$ maka $\sec 4^\circ $ = ….
A. $\frac{\sqrt{2(a^2+1)}}{a+1}$
B. $\frac{2\sqrt{(a^2+1)}}{a+1}$
C. $\frac{\sqrt{2(a^2+1)}}{a+1}$
D. $\frac{a-1}{\sqrt{2(a^2+1)}}$
E. $\frac{a+1}{\sqrt{2(a^2+1)}}$

Penyelesaian: Lihat/Tutup

$\begin{align}\cot 49^\circ &= \frac{1}{a} \\ \tan 49^\circ &= a \\ \tan (45^\circ +4^\circ ) &= a \\ \frac{\tan 45^\circ +\tan 4^\circ }{1-\tan 45^\circ .\tan 4^\circ } &= a \\ \frac{1+\tan 4^\circ }{1-1.\tan 4^\circ } &= a \\ a-a\tan 4^\circ &= 1+\tan 4^\circ \\ -a\tan 4^\circ -\tan 4^\circ &= 1-a \\ a\tan 4^\circ +\tan 4^\circ &= a-1 \\ (a+1)\tan 4^\circ &= a-1 \\ \tan 4^\circ &= \frac{a-1}{a+1}=\frac{de}{sa} \end{align}$
$\begin{align}\sec 4^\circ &= \frac{mi}{sa} \\ &= \frac{\sqrt{de^2+sa^2}}{sa} \\ &= \frac{\sqrt{{{(a-1)}^{2}}+{{(a+1)}^{2}}}}{a+1} \\ &= \frac{\sqrt{a^2-2a+1+a^2+2a+1}}{a+1} \\ &= \frac{\sqrt{2a^2+2}}{a+1} \\ \sec 4^\circ &= \frac{\sqrt{2(a^2+1)}}{a+1} \end{align}$
Jawaban: A

Soal No. 24

Jika $\tan \alpha =1$ dan $\tan \beta =\frac{1}{3}$ dengan $\alpha $ dan $\beta $ sudut lancip, maka $\sin (\alpha -\beta )$ = ….
A. $\frac{2}{3}\sqrt{5}$
B. $\frac{1}{5}\sqrt{5}$
C. $\frac{1}{2}$
D. $\frac{2}{5}$
E. $\frac{1}{5}$

Penyelesaian: Lihat/Tutup

$\tan \alpha =1\Leftrightarrow \tan \alpha =\frac{1}{1}=\frac{de}{sa}$
$\begin{align}mi &= \sqrt{de^2+sa^2} \\ &= \sqrt{1^2+1^2} \\ mi &= \sqrt{2} \end{align}$
$\sin \alpha =\frac{de}{mi}\Leftrightarrow \sin \alpha =\frac{1}{\sqrt{2}}$
$\cos \alpha =\frac{sa}{mi}\Leftrightarrow \cos \alpha =\frac{1}{\sqrt{2}}$
$\tan \beta =\frac{1}{3}=\frac{de}{sa}$
$\begin{align}mi &= \sqrt{de^2+sa^2} \\ &= \sqrt{{{1}^{2}}+3^2} \\ mi &= \sqrt{10} \end{align}$
$\sin \beta =\frac{de}{mi}\Leftrightarrow \sin \beta =\frac{1}{\sqrt{10}}$
$\cos \beta =\frac{sa}{mi}\Leftrightarrow \cos \beta =\frac{3}{\sqrt{10}}$
$\begin{align}\sin (\alpha -\beta ) &= \sin \alpha \cos \beta -\cos \alpha \sin \beta \\ &= \frac{1}{\sqrt{2}}.\frac{3}{\sqrt{10}}-\frac{1}{\sqrt{2}}.\frac{1}{\sqrt{10}} \\ &= \frac{3}{\sqrt{20}}-\frac{1}{\sqrt{20}} \\ &= \frac{2}{\sqrt{20}} \\ &= \frac{2}{2\sqrt{5}}\times \frac{\sqrt{5}}{\sqrt{5}} \\ \sin (\alpha -\beta ) &= \frac{1}{5}\sqrt{5} \end{align}$
Jawaban: B

Soal No. 25

Diketahui $\cos (x-y)=\frac{4}{5}$ dan $\sin x\sin y=\frac{3}{10}$. Nilai $\tan x\tan y$ = ….
A. $-\frac{5}{3}$
B. $-\frac{4}{3}$
C. $-\frac{3}{5}$
D. $\frac{3}{5}$
E. $\frac{5}{3}$

Penyelesaian: Lihat/Tutup

$\begin{align}\cos (x-y) &= \frac{4}{5} \\ \cos x\cos y+\sin x\sin y &= \frac{4}{5} \\ \cos x\cos y+\frac{3}{10} &= \frac{4}{5} \\ \cos x\cos y &= \frac{4}{5}-\frac{3}{10} \\ \cos x\cos y &= \frac{5}{10} \end{align}$
$\begin{align}\tan x\tan y &= \frac{\sin x}{\cos x}.\frac{\sin y}{\cos y} \\ &= \frac{\sin x\sin y}{\cos x\cos y} \\ &= \frac{\frac{3}{10}}{\frac{5}{10}} \\ \tan x\tan y &= \frac{3}{5} \end{align}$
Jawaban: D

Soal No. 26

Jika $\alpha $ dan $\beta $ sudut lancip, $\cos (\alpha -\beta )=\frac{1}{2}\sqrt{3}$ dan $\cos \alpha \cos \beta =\frac{1}{2}$, maka $\frac{\cos (\alpha +\beta )}{\cos (\alpha -\beta )}$ = ….
A. $2-\sqrt{3}$
B. $1-\frac{1}{3}\sqrt{3}$
C. $3-2\sqrt{3}$
D. $1-\frac{1}{2}\sqrt{3}$
E. $\frac{2}{3}\sqrt{3}-1$

Penyelesaian: Lihat/Tutup

$\begin{align}\cos (\alpha -\beta ) &= \frac{1}{2}\sqrt{3} \\ \cos \alpha \cos \beta +\sin \alpha \sin \beta &= \frac{1}{2}\sqrt{3} \\ \frac{1}{2}+\sin \alpha \sin \beta &= \frac{1}{2}\sqrt{3} \\ \sin \alpha \sin \beta &= \frac{1}{2}\sqrt{3}-\frac{1}{2} \end{align}$
$\begin{align}\cos (\alpha +\beta ) &= \cos \alpha \cos \beta -\sin \alpha \sin \beta \\ &= \frac{1}{2}-\left( \frac{1}{2}\sqrt{3}-\frac{1}{2} \right) \\ &= 1-\frac{1}{2}\sqrt{3} \\ \cos (\alpha +\beta ) &= \frac{2-\sqrt{3}}{2} \end{align}$
$\begin{align}\frac{\cos (\alpha +\beta )}{\cos (\alpha -\beta )} &= \frac{\frac{2-\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}} \\ &= \frac{2-\sqrt{3}}{2}\times \frac{2}{\sqrt{3}} \\ &= \frac{2-\sqrt{3}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ &= \frac{2\sqrt{3}-3}{3} \\ \frac{\cos (\alpha +\beta )}{\cos (\alpha -\beta )} &= \frac{2}{3}\sqrt{3}-1 \end{align}$
Jawaban: E

Soal No. 27

Diketahui segitiga ABC dengan $\tan A=3$, $\tan B=1$, maka nilai $\tan C$ = ….
A. 2
B. 1
C. $-\frac{1}{2}$
D. $-2$
E. $-3$

Penyelesaian: Lihat/Tutup

$\tan A=3\Leftrightarrow \tan A=\frac{3}{1}=\frac{de}{sa}$
$\begin{align}A+B+C &= 180^\circ \\ C &= 180^\circ -(A+B) \\ \tan C &= \tan (180^\circ -(A+B)) \\ &= -\tan (A+B) \\ &= -\left( \frac{\tan A+\tan B}{1-\tan A\tan B} \right) \\ &= -\left( \frac{3+1}{1-3.1} \right) \\ \tan C &= 2 \end{align}$
Jawaban: A

Soal No. 28

Jika $\tan 3^\circ =p$ maka $\tan 228^\circ $ adalah ….
A. $\frac{(1-p)^2}{1-p^2}$
B. $\frac{(1-p)^2}{p^2-1}$
C. $\frac{p^2-1}{(1-p)^2}$
D. $\frac{1-p^2}{(1-p)^2}$
E. $\frac{1-p^2}{1+p^2}$

Penyelesaian: Lihat/Tutup

$\begin{align}\tan 228^\circ &= \tan (225^\circ +3^\circ ) \\ &= \frac{\tan 225^\circ +\tan 3^\circ }{1-\tan 225^\circ \tan 3^\circ } \\ &= \frac{1+p}{1-1.p} \\ &= \frac{1+p}{1-p}\times \frac{1-p}{1-p} \\ \tan 228^\circ &= \frac{1-p^2}{(1-p)^2} \end{align}$
Jawaban: D

Soal No. 29

Perhatikan gambar berikut!

$\sin (x+y)$ = ….
A. $\frac{117}{125}$
B. $\frac{44}{125}$
C. $\frac{13}{125}$
D. $\frac{8}{25}$
E. $\frac{4}{5}$

Penyelesaian: Lihat/Tutup

Perhatikan segitiga PSR:
$\begin{align}PS &= \sqrt{PR^2-RS^2} \\ &= \sqrt{25^2-7^2} \\ PS &= 24 \end{align}$
$\sin y=\frac{RS}{PR}\Leftrightarrow \sin y=\frac{7}{25}$
$\cos y=\frac{PS}{PR}\Leftrightarrow \cos y=\frac{24}{25}$
Perhatikan segitiga PQR:
$\begin{align}PQ &= \sqrt{PR^2-QR^2} \\ &= \sqrt{25^2-15^2} \\ PQ &= 20 \end{align}$
$\sin x=\frac{QR}{PR}=\frac{15}{25}=\frac{3}{5}$
$\cos x=\frac{PQ}{PR}=\frac{20}{25}=\frac{4}{5}$
$\begin{align}\sin (x+y) &= \sin x\cos y+\cos x\sin y \\ &= \frac{3}{5}.\frac{24}{25}+\frac{4}{5}.\frac{7}{25} \\ &= \frac{72}{125}+\frac{28}{125} \\ &= \frac{100}{125} \\ \sin (x+y) &= \frac{4}{5} \end{align}$
Jawaban: E

Soal No. 30

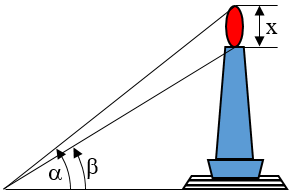
Seseorang mencoba menentukan tinggi nyala api di puncak tugu Monas di Jakarta dengan cara mengukur sudut lihat dari suatu tempat sejauh $a$ dari kaki tugu itu $\alpha $ dan $\beta $ seperti dalam gambar. Jika $x$ tinggi nyala api itu, maka $x$ = …

A. $a\sin (\alpha -\beta )$
B. $a\tan (\alpha -\beta )$
C. $a\cot (\alpha -\beta )$
D. $\frac{a\sin (\alpha -\beta )}{\sin \alpha \sin \beta }$
E. $\frac{a\sin (\alpha -\beta )}{\cos \alpha \cos \beta }$

Penyelesaian: Lihat/Tutup

$\begin{align}\tan \alpha &= \frac{x+y}{a} \\ x+y &= a\tan \alpha \\ y &= a\tan \alpha -x \end{align}$
$\begin{align}\tan \beta &= \frac{y}{a} \\ \tan \beta &= \frac{a\tan \alpha -x}{a} \\ a\tan \beta &= a\tan \alpha -x \\ x &= a\tan \alpha -a\tan \beta \\ x &= a(\tan \alpha -\tan \beta ) \\ x &= a\left( \frac{\sin \alpha }{\cos \alpha }-\frac{\sin \beta }{\cos \beta } \right) \\ x &= a\left( \frac{\sin \alpha \cos \beta -\cos \alpha \sin \beta }{\cos \alpha \cos \beta } \right) \\ x &= \frac{a\sin (\alpha -\beta )}{\cos \alpha \cos \beta } \end{align}$
Jawaban: E

Semoga postingan: Soal Trigonometri Jumlah dan Selisih Dua Sudut dan Pembahasan ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :