Soal Barisan dan Deret Aritmetika Pembahasan
Hallo...! Pengunjung setia Catatan Matematika, kali ini Bang RP (Reikson Panjaitan, S.Pd) berbagi Kumpulan Soal Barisan dan Deret Aritmetika beserta pembahasannya. Ayo... manfaatkan website Catatan Matematika ini untuk belajar matematika secara online.
A. $-4$
B. $-2$
C. 0
D. 2
E. 4
$2a+b$, $6a+b$, $14a+b$
Syarat barisan aritmetika:
$\begin{align}U_2-U_1 &= U_3-U_2 \\ 2U_2 &= U_1+U_3 \\ 2(6a+b) &= 2a+b+14a+b \\ 12a+2b &= 16a+2b \\ 12a-16a &= 2b-2b \\ -4a &= 0 \\ a &= 0 \end{align}$
Jawaban: C
A. $\frac{1}{4}$
B. $\frac{1}{3}$
C. $\frac{3}{4}$
D. 3
E. 2
Syarat barisan aritmetika: $U_2-U_1=U_3-U_2=U_4-U_3$
$\begin{align}U_3-U_2 &= U_4-U_3 \\ 2U_3 &= U_2+U_4 \\ 2w &= y+2y \\ 2w &= 3y \end{align}$
$\begin{align}U_2-U_1 &= U_3-U_2 \\ 2U_2 &= U_1+U_3 \\ 2y &= x+w|\,kedua\,ruas\,\times 2 \\ 4y &= 2x+2w \\ 4y &= 2x+3y \\ 4y-3y &= 2x \\ y &= 2x \end{align}$
Nilai $\frac{y}{x}=\frac{2x}{x}\Leftrightarrow \frac{y}{x}=2$
Jawaban: E
A. 50
B. 52
C. 74
D. 77
E. 78
$a=2$
$\begin{align}b &= U_2-U_1 \\ &= 5-2 \\ b &= 3 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{25} &= 2+(25-1).3 \\ &= 2+72 \\ U_{25} &= 74 \end{align}$
Jawaban: C
A. 12
B. 6
C. 0
D. $-6$
E. $-12$
$a=36$, $U_{12}=-30$, $U_7$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_{12} &= -30 \\ a+11b &= -30 \\ 36+11b &= -30 \\ 11b &= -30-36 \\ 11b &= -66 \\ b &= -6 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_7 &= a+6b \\ &= 36+6.(-6) \\ &= 36-36 \\ U_7 &= 0 \end{align}$
Jawaban: C
A. 24
B. 25
C. 26
D. 27
E. 28
$U_2=5\to a+b=5\,....\,(1)$
$\begin{align}U_4+U_6 &= 28 \\ (a+3b)+(a+5b) &= 28 \\ 2a+8b &= 28 \\ a+4b &= 14\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2) maka:
$\frac{\begin{align}a+b &= 5 \\ a+4b &= 14 \end{align}}{\begin{align}-3b &= -9 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan (1):
$\begin{align}a+b &= 5 \\ a+3 &= 5 \\ a &= 2 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_9 &= a+8b \\ &= 2+8.3 \\ U_9 &= 26 \end{align}$
Jawaban: C
A. 175
B. 189
C. 275
D. 295
E. 375
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_5 &= 21 \\ a+4b &= 21 \\ a+4.4 &= 21 \\ a+16 &= 21 \\ a &= 21-16 \\ a &= 5 \end{align}$
$\begin{align}U_t &= 25 \\ a+(t-1)b &= 25 \\ 5+(t-1).4 &= 25 \\ 5+4t-4 &= 25 \\ 4t &= 24 \\ t &= 6 \end{align}$
Ingat, $t=\frac{n+1}{2}$ maka:
$\begin{align}\frac{n+1}{2} &= t \\ \frac{n+1}{2} &= 6 \\ n+1 &= 12 \\ n &= 11 \end{align}$
$\begin{align}S_n &= n.U_t \\ S_{11} &= 11\times 25 \\ &= 275 \end{align}$
Jawaban: C
A. 43
B. 53
C. 67
D. 147
E. 240
$\begin{align}U_n &= S_n-S_{n-1} \\ U_{10} &= S_{10}-S_9 \\ &= (3.10^2-4.10)-(3.9^2-4.9) \\ &= (300-40)-(243-36) \\ &= 260-207 \\ U_{10} &= 53 \end{align}$
Jawaban: B
A. 205
B. 340
C. 410
D. 610
E. 900
$\frac{\begin{align}U_7=a+6b &= 43 \\ U_2=a+b &= 13 \end{align}}{\begin{align}5b &= 30 \\ b &= 6 \end{align}}-$
Substitusi $b=6$ ke persamaan $a+b=13$ maka:
$\begin{align}a+b &= 13 \\ a+6 &= 13 \\ a &= 7 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{10} &= \frac{10}{2}(2.7+(10-1).6) \\ &= 5(14+54) \\ &= 5(68) \\ S_{10} &= 340 \end{align}$
Jawaban: B
A. 45.692
B. 54.396
C. 66.661
D. 73.775
E. 80.129
$\left\lfloor x \right\rfloor $ = bilangan bulat terbesar yang lebih kecil atau sama dengan $x$.
$\left\lceil x \right\rceil $ = bilangan bulat terkecil yang lebih besar atau sama dengan $x$.
$\begin{align}a &= \left\lfloor \frac{250}{7}+1 \right\rfloor \times 7 \\ &= \left\lfloor 35,71+1 \right\rfloor \times 7 \\ &= \left\lfloor 36,71 \right\rfloor \times 7 \\ &= 36\times 7 \\ a &= 252 \end{align}$
$\begin{align}U_n &= \left\lceil \frac{1.000}{7}-1 \right\rceil \times 7 \\ &= \left\lceil 142,86-1 \right\rceil \times 7 \\ &= \left\lceil 141,86 \right\rceil \times 7 \\ &= 142\times 7 \\ U_n &= 994 \end{align}$
Karena ini adalah deret bilangan yang habis dibagi 7 maka $b=7$
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_n &= 994 \\ a+(n-1)b &= 994 \\ 252+(n-1)7 &= 994 \\ 7(n-1) &= 742 \\ n-1 &= 106 \\ n &= 107 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(a+U_n) \\ S_{107} &= \frac{107}{2}(252+994) \\ &= \frac{107}{2}(1.246) \\ &= 107\times 623 \\ S_{107} &= 66.661 \end{align}$
Jawaban: C
A. $S_n=\frac{n}{2}(3n-7)$
B. $S_n=\frac{n}{2}(3n-5)$
C. $S_n=\frac{n}{2}(3n-4)$
D. $S_n=\frac{n}{2}(3n-3)$
E. $S_n=\frac{n}{2}(3n-2)$
$\begin{align}a &= U_1 \\ &= 3.1-5 \\ a &= -2 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(a+U_n) \\ &= \frac{n}{2}(-2+3n-5) \\ S_n &= \frac{n}{2}(3n-7) \end{align}$
Jawaban: A
A. $n\log a(n+1)$
B. $n(n+1)\log a$
C. $\frac{1}{2}n\log a(n+1)$
D. $\frac{1}{2}n(n+1)\log a$
E. $\frac{1}{2}n(n-1)\log a$
$\begin{align}U_2-U_1 &= \log a^2-\log a \\ &= 2\log a-\log a \\ U_2-U_1 &= \log a \end{align}$
$\begin{align}U_3-U_2 &= \log a^3-\log a^2 \\ &= 3\log a-2\log a \\ U_3-U_2 &= \log a \end{align}$
Karena $U_2-U_1=U_3-U_2$ maka deret tersebut merupakan deret aritmetika dengan:
$U_1=\log a$ dan $U_n=\log a^n$ maka:
$\begin{align}S_n &= \frac{n}{2}(U_1+U_n) \\ &= \frac{1}{2}n(\log a+\log a^n) \\ &= \frac{n}{2}(\log a+n\log a) \\ S_n &= \frac{1}{2}n(n+1)\log a \end{align}$
Jawaban: D
A. 50
B. 80
C. 100
D. 200
E. 400
$a+5b$ + $a+8b$ + $a+11b$ + $a+14b$ = 20
$4a+38b=20$
$2a+19b=10$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b \\ S_{20} &= \frac{20}{2}(2a+(20-1)b) \\ &= 10(2a+19b) \\ &= 10.10 \\ S_{20} &= 100 \end{align}$
Jawaban: C
A. $-\frac{11}{2}$
B. $-2$
C. 2
D. $\frac{5}{2}$
E. $\frac{11}{2}$
$\begin{align}U_1 &= S_1 \\ &= 1^2+\frac{5}{2}.1 \\ U_1 &= \frac{7}{2} \end{align}$
$\begin{align}U_n &= S_n-S_{n-1} \\ U_2 &= S_2-S_1 \\ &= \left( 2^2+\frac{5}{2}.2 \right)-\left( 1^2+\frac{5}{2}.1 \right) \\ &= \left( 4+5 \right)-\left( 1+\frac{5}{2} \right) \\ &= 9-\frac{7}{2} \\ U_2 &= \frac{11}{2} \end{align}$
$\begin{align}b &= U_2-U_1 \\ &= \frac{11}{2}-\frac{7}{2} \\ b &= \frac{5}{2} \end{align}$
Jawaban: D
A. 9
B. 10
C. 19
D. 20
E. 40
Tali terpendek = $a$ = 2 cm
Panjang tali semula = $S_5$= 200 cm
Panjang tali ketiga = $U_3$ = …?
Ingat, $S_n=\frac{n}{2}(2a+(n-1)b)$ maka:
$\begin{align}S_5 &= 200 \\ \frac{5}{2}(2.2+(5-1)b) &= 200 \\ 5(4+4b) &= 400 \\ 4+4b &= 80 \\ 4b &= 76 \\ b &= 19 \end{align}$
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_3 &= a+2b \\ &= 2+2.19 \\ U_3 &= 40 \end{align}$
Jawaban: E
A. 8
B. 16
C. 20
D. 24
E. 32
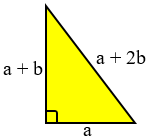
$\begin{align}a+2b &= 40 \\ a+b+b &= 40 \\ a+b &= 40-b \end{align}$
$a+2b=40\to a=40-2b$
Karena $a$ adalah salah satu panjang sisi segitiga maka:
$\begin{align}a > 0 \\ 40-2b > 0 \\ -2b > -40 \\ b < 20 \end{align}$
Dengan menggunakan teorema pythagoras maka:
$\begin{align}(a+2b)^2 &= a^2+(a+b)^2 \\ 40^2 &= (40-2b)^2+(40-b)^2 \\ 1600 &= 1600-160b+4b^2+1600-80b+b^2 \\ 0 &= 5b^2-240b+1600 \\ 0 &= b^2-48b+320 \\ 0 &= (b-40)(b-8) \end{align}$
$b-8=0\to b=8$ (memenuhi)
$b-40=0\to b=40$ (tidak memenuhi)
Panjang sisi siku-siku terpendek adalah:
$\begin{align}a &= 40-2b \\ &= 40-2.8 \\ a &= 24 \end{align}$
Jadi, panjang sisi siku-siku terpendek adalah 24 cm.
Cara alternatif:
Jika panjang sisi-sisi segitiga membentuk barisan aritmetika maka ketiga sisinya adalah $3x$, $4x$ dan $5x$ untuk $x > 0$, maka:
Sisi terpanjang = 40
$5x=40\to x=8$
Sisi terpendek = $3x=3.8=24$ cm.
Jawaban: D
A. 1.200
B. 800
C. 720
D. 600
E. 300
Banyak baris di belakang lebih 4 kursi dari baris di depannya maka $b=4$.
Dalam gedung pertunjukan terdapat 15 baris maka $n=15$.
Baris terdepan ada 20 kursi $a=20$
Kapasitas gedung pertunjukan tersebut adalah $S_{15}$ = …?
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{15} &= \frac{15}{2}(2.20+14.4) \\ &= \frac{15}{2}(40+56) \\ &= \frac{15}{2}\times 96 \\ S_{15} &= 720 \end{align}$
Kapasitas gedung pertunjukan tersebut adalah 720 tempat duduk.
Jawaban: C
A. Rp25.800.000,00
B. Rp25.200.000,00
C. Rp25.000.000,00
D. Rp18.800.000,00
E. Rp18.000.000,00
$n$ = 10 tahun
$a$ = Rp1.600.000,00
$b$ = Rp200.000,00
$S_{10}$ = ….
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{10} &= \frac{10}{2}(2(1.600.000)+9.(200.000)) \\ &= 5(3.200.000+1.800.000) \\ &= 5(5.000.000) \\ S_{10} &= 25.000.000 \end{align}$
Jawaban: C
A. 45.760
B. 45.000
C. 16.960
D. 16.000
E. 9.760
Tiap tahun produksi turun sebesar 120 unit maka $b=-120$.
$S_{16}$ = …?
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{16} &= \frac{16}{2}(2(1.960)+15(-120)) \\ &= 8(3.920-1.800) \\ &= 8\times 2.120 \\ S_{16} &= 16.960 \end{align}$
Jawaban: C
A. Rp1.740.000,00
B. Rp1.750.000,00
C. Rp1.840.000,00
D. Rp1.950.000,00
E. Rp2.000.000,00
$b$ = Rp18.000,00
$S_{12}$ = ….
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{12} &= \frac{12}{2}(2(46.000)+11(18.000)) \\ &= 6(92.000+198.000) \\ &= 6(290.000) \\ S_{12} &= 1.740.000 \end{align}$
Jawaban: A
A. 112
B. 115
C. 125
D. 130
E. 160
Usia anak termuda 13 tahun maka $a=13$.
Usia anak tertua 33 tahun maka $U_5=33$.
Jumlah usia mereka = $S_5$ = …?
$\begin{align}S_n &= \frac{n}{2}(a+U_n) \\ S_5 &= \frac{5}{2}(a+U_5) \\ &= \frac{5}{2}(13+33) \\ &= 5\times 23 \\ S_5 &= 115 \end{align}$
Jadi, jumlah usia mereka adalah 115 tahun.
Jawaban: B
A. 8(7 + n)
B. 4(7 + n)
C. 8(7 – n)
D. 4(7 – n)
E. 7(8 – 4n)
$(3k+12)$, $(2k+16)$, $(44-k)$, …
Syarat barisan aritmetika:
$\begin{align}U_2-U_1 &= U_3-U_2 \\ 2U_2 &= U_1+U_3 \\ 2(2k+16) &= 3k+12+44-k \\ 4k+32 &= 2k+56 \\ 4k-2k &= 56-32 \\ 2k &= 24 \\ k &= 12 \end{align}$
$\begin{align}U_1 &= 3k+12 \\ &= 3.12+12 \\ U_1 &= 48=a \end{align}$
$\begin{align}U_2 &= 2k+16 \\ &= 2.12+16 \\ U_2 &= 40 \end{align}$
$\begin{align}b &= U_2-U_1 \\ &= 40-48 \\ b &= -8 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ &= 48+(n-1).(-8) \\ &= 48-8n+8 \\ &= 56-8n \\ U_n &= 8(7-n) \end{align}$
Jawaban: C
A. $-6$
B. $-5$
C. 5
D. 6
E. 30
Barisan aritmetika: $U_n=a+(n-1)b$
$\frac{\begin{align}U_4 = a+3b &= 56 \\ U_9 = a+8b &= 26 \end{align}}{\begin{align}-5b &= 30 \\ b &= -6 \end{align}}-$
Jadi, beda barisan tersebut adalah $-6$.
Jawaban: A
A. 171
B. 179
C. 187
D. 195
E. 203
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_3=a+2b &= -5 \\ U_10=a+9b &= 51 \end{align}}{\begin{align}-7b &= -56 \\ b &= 8 \end{align}}-$
Substitusi $b=8$ ke persamaan $a+2b=-5$ maka:
$\begin{align}a+2b &= -5 \\ a+2.8 &= -5 \\ a+16 &= -5 \\ a &= -5-16 \\ a &= -21 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{28} &= a+27b \\ &= -21+27.8 \\ &= -21+216 \\ U_{28} &= 195 \end{align}$
Jawaban: D
A. 18
B. 24
C. 28
D. 34
E. 43
$U_2+U_4=26$, $U_8-U_5=9$, $U_{10}$ = ….
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_2+U_4 &= 26 \\ (a+b)+(a+3b) &= 26 \\ 2a+4b &= 26 \\ a+2b &= 13 \end{align}$
$\begin{align}U_8-U_5 &= 9 \\ (a+7b)-(a+4b) &= 9 \\ 3b &= 9 \\ b &= 3 \end{align}$
Substitusi ke persamaan $a+2b=13$ maka:
$\begin{align}a+2b &= 13 \\ a+2.3 &= 13 \\ a+6 &= 13 \\ a &= 7 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{10} &= a+9b \\ &= 7+9.3 \\ &= 7+27 \\ U_{10} &= 34 \end{align}$
Jawaban: D
A. 32
B. 36
C. 40
D. 44
E. 48

Dengan menggunakan teorema pythagoras maka:
$\begin{align}(a+2b)^2 &= a^2+(a+b)^2 \\ a^2+4ab+4b^2 &= a^2+a^2+2ab+b^2 \\ a^2-2ab-3b^2 &= 0 \\ a^2+ab-3ab-3b^2 &= 0 \\ a(a+b)-3b(a+b) &= 0 \\ (a+b)(a-3b) &= 0 \end{align}$
Perhatikan, $a+b > 0$ maka $a-3b=0\Leftrightarrow a=3b$
Luas segitiga = 54 maka:
$\begin{align}L &= 54 \\ \frac{1}{2}a(a+b) &= 54 \\ a(a+b) &= 108 \\ 3b(3b+b) &= 108 \\ 12b^2 &= 0 \\ b^2 &= 9 \\ b &= 3 \end{align}$
$a=3b\Leftrightarrow a=3.3=9$
$\begin{align}K &= a+(a+b)+(a+2b) \\ &= 3a+3b \\ &= 3.9+3.3 \\ K &= 36 \end{align}$
Jadi, keliling segitiga tersebut adalah 36 cm.
Cara alternatif:
Jika panjang sisi-sisi segitiga membentuk barisan aritmetika maka ketiga sisinya adalah $3x$, $4x$ dan $5x$ untuk $x>0$.
$\begin{align}L &= 54 \\ \frac{1}{2}.3x.4x &= 54 \\ 6x^2 &= 54 \\ x^2 &= 9 \\ x &= 3 \end{align}$
$\begin{align}K &= 3x+4x+5x \\ &= 12x \\ &= 12.3 \\ K &= 36 \end{align}$
Jawaban: B
A. 27
B. 30
C. 32
D. 35
E. 41
$t=\frac{n+1}{2}=\frac{21+1}{2}\Leftrightarrow t=11$
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_t &= 52 \\ U_{11} &= 52 \\ a+10b &= 52\,....\,(1) \end{align}$
$\begin{align}U_3+U_5+U_{15} &= 106 \\ (a+2b)+(a+4b)+(a+14b) &= 106 \\ 3a+20b &= 106\,....(2) \end{align}$
Eliminasi $b$ dari persamaan (2) dan (1):
$\left. \begin{align}3a+20b &= 106 \\ a+10b &= 52 \end{align} \right|\begin{matrix} \times 1 \\ \times 2 \\ \end{matrix}$
$\frac{\begin{align}3a+20b &= 106 \\ 2a+20b &= 104 \\ \end{align}}{a=2}-$
Substitusi $a=2$ ke persamaan (1):
$\begin{align}a+10b &= 52 \\ 2+10b &= 52 \\ 10b &= 50 \\ b &= 5 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_7 &= a+6b \\ &= 2+6.5 \\ U_7 &= 32 \end{align}$
Jawaban: C
A. Rp15.000,00
B. Rp17.500,00
C. Rp20.000,00
D. Rp22.500,00
E. Rp25.000,00
$a$ = jumlah uang yang diterima anak pertama dan $b=-5.000$
Ingat, $S_n=\frac{n}{2}(2a+(n-1)b)$ maka:
$\begin{align}S_4 &= 100.000 \\ \frac{4}{2}(2a+3b) &= 100.000 \\ 2a+3b &= 50.000 \\ 2a+3(-5.000) &= 50.000 \\ 2a-15.000 &= 50.000 \\ 2a &= 65.000 \\ a &= 32.500 \end{align}$
Si bungsu = anak ke-4.
Jumlah uang yang diterima oleh si bungsu adalah $U_4$.
$\begin{align}U_n &= a+(n-1)b \\ U_4 &= a+3b \\ &= 32.500+3(-5.000) \\ &= 32.500-15.000 \\ U_4 &= 17.500 \end{align}$
Jawaban: B
A. $-35$
B. $-25$
C. 0
D. 25
E. 35
$\frac{\begin{align}U_2=a+b &= 7\, \\ U_5=a+4b &= -2 \\ \end{align}}{\begin{align}-3b &= 9 \\ b &= -3 \end{align}}-$
Substitusi $b=-3$ ke persamaan $a+b=7$ maka:
$\begin{align}a+b &= 7 \\ a+(-3) &= 7 \\ a &= 10 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{10} &= \frac{10}{2}(2a+9b) \\ &= 5(2.10+9.(-3)) \\ &= 5(20-27) \\ S_{10} &= -35 \end{align}$
Jawaban: A
A. 35
B. 36
C. 37
D. 38
E. 39
$\begin{align}U_n &= S_n-S_{n-1} \\ U_{10} &= S_{10}-S_9 \\ &= (2.10^2-10)-(2.9^2-9) \\ &= 190-153 \\ U_{10} &= 37 \end{align}$
Jawaban: C
A. 45.500
B. 48.000
C. 50.500
D. 51.300
E. 55.500
$U_n$ = jumlah produksi dalam bulan ke-n
$U_1=4.000=a$
$U_2=4.050$
$S_{12}$ = …?
$\begin{align}b &= U_2-U_1 \\ &= 4.050-4.000 \\ b &= 50 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{12} &= \frac{12}{2}(2a+11b) \\ &= 6(2\times 4.000+11\times 50) \\ &= 6\times 8.550 \\ S_{12} &= 51.300 \end{align}$
Jawaban: D
A. 1.050
B. 1.200
C. 1.350
D. 1.650
E. 1.750
$a=120$, $b=10$, $S_{10}$ = ….
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{10} &= \frac{10}{2}(2a+11b) \\ &= 5(2\times 120+11\times 10) \\ &= 5\times 350 \\ S_{10} &= 1.750 \end{align}$
Jawaban: E
A. 38
B. 40
C. 42
D. 44
E. 46
$U_3=10$, $U_7=26$, $U_{10}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_3=a+2b &= 10 \\ U_7=a+6b &= 26 \\ \end{align}}{\begin{align}-4b &= -16 \\ b &= 4 \end{align}}-$
Substitusi $b=4$ ke persamaan $a+2b=10$ maka:
$\begin{align}a+2b &= 10 \\ a+2.4 &= 10 \\ a &= 2 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{10} &= a+9b \\ &= 2+9.4 \\ U_{10} &= 38 \end{align}$
Jawaban: A
A. 77
B. 76
C. 75
D. 67
E. 66
$U_3=7$, $U_8=27$, $U_{20}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_3=a+2b &= 7 \\ U_8=a+7b &= 27 \\ \end{align}}{\begin{align}-5b &= -20 \\ b &= 4 \end{align}}-$
Substitusi $b=4$ ke persamaan $a+2b=7$ maka:
$\begin{align}a+2b &= 7 \\ a+2.4 &= 7 \\ a &= -1 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{20} &= a+19b \\ &= -1+19.4 \\ U_{20} &= 75 \end{align}$
Jawaban: C
A. 35
B. 38
C. 39
D. 40
E. 42
$U_4=5$, $U_7=14$, $U_{15}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_4=a+3b &= 5 \\ U_7=a+6b &= 14 \\ \end{align}}{\begin{align}-3b &= -9 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan $a+3b=5$ maka:
$\begin{align}a+3b &= 5 \\ a+3.3 &= 5 \\ a &= -4 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{15} &= a+14b \\ &= -4+14\times 3 \\ U_{15} &= 38 \end{align}$
Jawaban: B
A. Rp1.470.000,00
B. Rp1.550.000,00
C. Rp1.632.000,00
D. Rp1.650.000,00
E. Rp1.675.000,00
$U_n$ = banyaknya kue yang dibuat pada hari ke-n.
$U_1=20=a$ dan $U_2=22$
Keuntungan = Rp1.000,00/kue.
Keuntungan Rini daam 31 hari pertama adalah 1000 x Jumlah kue yang dibuat selama 31 hari pertama = $1.000\times S_{31}$ = …
$b=U_2-U_1=22-20\Leftrightarrow b=2$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{31} &= \frac{31}{2}(2a+30b) \\ &= \frac{31}{2}(2\times 20+30\times 2) \\ &= \frac{31}{2}\times 100 \\ S_{31} &= 15.500 \end{align}$
Keuntungan Rini selama 31 hari pertama adalah $1.000\times S_{31}$ = $1.000\times 15.500$ = 15.500.000,00.
Jawaban: B
A. Rp6.750.000,00
B. Rp7.050.000,00
C. Rp7.175.000,00
D. Rp7.225.000,00
E. Rp7.300.000,00
$U_2$ = Rp925.000,00
$\begin{align}b &= U_2-U_1 \\ &= 925.000-1.000.000 \\ b &= -75.000 \end{align}$
Jumlah seluruh uang yang telah diambil selama 12 bulan pertama adalah $S_{12}$.
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{12} &= \frac{12}{2}(2a+11b) \\ &= 6(2(1.000.000)+11(-75.000)) \\ &= 6(2.000.000-825.000) \\ &= 6(1.175.000) \\ S_{12} &= 7.050.000 \end{align}$
Jawaban: B
A. 2
B. 6
C. 10
D. 14
E. 18
$\begin{align}U_n &= S_n-S_{n-1} \\ U_4 &= S_4-S_3 \\ &= (2.4^2-12.4)-(2.3^2-12.3) \\ &= -16-(-18) \\ U_4 &= 2 \end{align}$
Jawaban: A
A. 62
B. 68
C. 72
D. 74
E. 76
$U_5=22$, $U_{12}=57$, $U_{15}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_5=a+4b &= 22 \\ U_{12}=a+11b &= 57 \end{align}}{\begin{align}-7b &= -35 \\ b &= 5 \end{align}}-$
Substitusi $b=5$ ke persamaan $a+4b=22$ maka:
$\begin{align}a+4b &= 22 \\ a+4.5 &= 22 \\ a &= 2 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{15} &= a+14b \\ &= 2+14.5 \\ U_{15} &= 72 \end{align}$
Jawaban: C
A. 382
B. 395
C. 400
D. 420
E. 435
$a=2$, $U_5=10$, $S_{20}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_5 &= 10 \\ a+4b &= 10 \\ 2+4b &= 10 \\ 4b &= 8 \\ b &= 2 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{20} &= \frac{20}{2}(2a+19b) \\ &= 10(2a+19b) \\ &= 10(2.2+19.2) \\ &= 10(4+38) \\ S_{20} &= 420 \end{align}$
Jawaban: D
A. 39
B. 45
C. 75
D. 78
E. 87
$\begin{align}U_n &= S_n-S_{n-1} \\ U_7 &= S_7-S_6 \\ &= (6.7^2-3.7)-(6.6^2-3.6) \\ &= 273-198 \\ U_7 &= 75 \end{align}$
Jawaban: C
A. 308
B. 318
C. 326
D. 344
E. 354
$U_4=110$, $U_9=150$, $U_{30}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_4=a+3b &= 110 \\ U_9=a+8b &= 150 \end{align}}{\begin{align}-5b &= -40 \\ b &= 8 \end{align}}-$
Substitusi $b=8$ ke persamaan $a+3b=110$ maka:
$\begin{align}a+3b &= 110 \\ a+3.8 &= 110 \\ a+24 &= 110 \\ a &= 86 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{30} &= a+29b \\ &= 86+29\times 8 \\ U_{30} &= 318 \end{align}$
Jawaban: B
A. 245
B. 255
C. 265
D. 285
E. 355
$U_6=35$, $U_{12}=65$, $U_{52}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_6=a+5b &= 35 \\ U_{12}=a+11b &= 65 \end{align}}{\begin{align}-6b &= -30 \\ b &= 5 \end{align}}-$
Substitusi $b=5$ ke persamaan $a+5b=35$ maka:
$\begin{align}a+5b &= 35 \\ a+5.5 &= 35 \\ a &= 10 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{52} &= a+51b \\ &= 10+51.5 \\ U_{52} &= 265 \end{align}$
Jawaban: C
A. 28
B. 32
C. 36
D. 40
E. 42
$U_3=9$, $U_5+U_7=36$, $U_{12}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$U_3=a+2b=9\,....\,(1)$
$\begin{align}U_5+U_7 &= 36 \\ (a+4b)+(a+6b) &= 36 \\ 2a+10b &= 36 \\ a+5b &= 18\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\frac{\begin{align}a+2b &= 9 \\ a+5b &= 18 \end{align}}{\begin{align}-3b &= -9 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan (1):
$\begin{align}a+2b &= 9 \\ a+2.3 &= 9 \\ a &= 3 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{12} &= a+11b \\ &= 3+11.3 \\ U_{12} &= 36 \end{align}$
Jawaban: C
A. 10
B. 19
C. 28,5
D. 55
E. 82,5
$\begin{align}U_2+U_{15}+U_{40} &= 165 \\ (a+b)+(a+14b)+(a+39b) &= 165 \\ 3a+54b &= 165 \\ a+18b &= 55 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{19} &= a+18b \\ &= 55 \end{align}$
Jawaban: D
A. 44
B. 42
C. 40
D. 38
E. 36
$\begin{align}U_n &= S_n-S_{n-1} \\ U_{20} &= S_{20}-S_{19} \\ &= (20^2+5.20)-(19^2+5.19) \\ &= 500-456 \\ U_{20} &= 44 \end{align}$
Jawaban: A
A. 176
B. 128
C. 88
D. 64
E. 18
$U_3=8$, $U_5=12$ maka $S_8$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_3=a+2b &= 8 \\ U_5=a+4b &= 12 \end{align}}{\begin{align}-2b &= -4 \\ b &= 2 \end{align}}-$
Substitusi $b=2$ ke persamaan $a+2b=8$ maka:
$\begin{align}a+2b &= 8 \\ a+2.2 &= 8 \\ a &= 4 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_8 &= \frac{8}{2}(2a+7b) \\ &= 4(2.4+7.2) \\ S_8 &= 88 \end{align}$
Jawaban: C
A. 150
B. 147
C. 146
D. 145
E. 137
$U_{11}+U_{17}=84$, $U_6+U_7=39$ maka $U_{50}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_{11}+U_{17} &= 84 \\ (a+10b)+(a+16b) &= 84 \\ 2a+26b &= 84\,....\,(1) \end{align}$
$\begin{align}U_6+U_7 &= 39 \\ (a+5b)+(a+6b) &= 39 \\ 2a+11b &= 39\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\frac{\begin{align}2a+26b &= 84 \\ 2a+11b &= 39 \end{align}}{\begin{align}15b &= 45 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan (2):
$\begin{align}2a+11b &= 39 \\ 2a+11.3 &= 39 \\ 2a+33 &= 39 \\ 2a &= 6 \\ a &= 3 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{50} &= a+49b \\ &= 3+49.3 \\ U_{50} &= 150 \end{align}$
Jawaban: A
A. 2
B. 3
C. 4
D. 5
E. 6
$\begin{align}U_n &= S_n-S_{n-1} \\ U_2 &= S_2-S_1 \\ &= \frac{3.2^2+2}{2}-\frac{3.1^2+1}{2} \\ &= 7-2 \\ U_2 &= 5 \end{align}$
$\begin{align}U_1 &= S_1 \\ &= \frac{3.1^2+1}{2} \\ U_1 &= 2 \end{align}$
$b=U_2-U_1=5-2\Leftrightarrow b=3$
Jawaban: B
A. 68
B. 72
C. 76
D. 80
E. 84
$U_5=11$, $U_8+U_{12}=52$ maka $S_8$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$U_5=a+4b=11\,....\,(1)$
$\begin{align}U_8+U_{12} &= 52 \\ (a+7b)+(a+11b) &= 52 \\ 2a+18b &= 52 \\ a+9b &= 26\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\frac{\begin{align}a+4b &= 11 \\ a+9b &= 26 \end{align}}{\begin{align}-5b &= -15 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan (1):
$\begin{align}a+4b &= 11 \\ a+4.3 &= 11 \\ a &= -1 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_8 &= \frac{8}{2}(2a+7b) \\ &= 4(2.(-1)+7.3) \\ &= 4\times 19 \\ S_8 &= 76 \end{align}$
Jawaban: C
A. 1.650
B. 1.710
C. 3.300
D. 4.280
E. 5.300
$U_6=17$, $U_{10}=33$ maka $S_{30}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_6=a+5b &= 17 \\ U_{10}=a+9b &= 33 \end{align}}{\begin{align}-4b &= -16 \\ b &= 4 \end{align}}-$
Substitusi $b=4$ ke persamaan $a+5b=17$ maka:
$\begin{align}a+5b &= 17 \\ a+5.4 &= 17 \\ a &= -3 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{30} &= \frac{30}{2}(2a+29b) \\ &= 15(2.(-3)+29.4) \\ &= 15\times 110 \\ S_{30} &= 1.650 \end{align}$
Jawaban: A
A. $-24$
B. $-12$
C. 33
D. 39
E. 66
$U_7=16$, $U_5=10$ maka $S_6$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_7=a+6b &= 16 \\ U_5=a+4b &= 10 \end{align}}{\begin{align}2b &= 6 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan $a+4b=10$ maka:
$\begin{align}a+4b &= 10 \\ a+4.3 &= 10 \\ a &= -2 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_6 &= \frac{6}{2}(2a+5b) \\ &= 3(2.(-2)+5.3) \\ &= 3(-4+15) \\ &= 3\times 11 \\ S_6 &= 33 \end{align}$
Jawaban: C
A. 30
B. 34
C. 40
D. 54
E. 84
$\begin{align}U_n &= S_n-S_{n-1} \\ U_4 &= S_4-S_3 \\ &= (3.4^2+19.4)-(3.3^2+19.3) \\ &= 124-84 \\ U_4 &= 40 \end{align}$
Jawaban: C
A. $-57$
B. $-56$
C. $-55$
D. $-53$
E. $-48$
$\begin{align}U_n &= S_n-S_{n-1} \\ U_8 &= S_8-S_7 \\ &= (3.8-4.8^2)-(3.7-4.7^2) \\ &= -232-(-175) \\ U_8 &= -57 \end{align}$
Jawaban: A
A. 20
B. 26
C. 36
D. 40
E. 42
$U_2=5$, $U_4+U_6=28$ maka $U_9$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$U_2=a+b=5\,....\,(1)$
$\begin{align}U_4+U_6 &= 28 \\ (a+3b)+(a+5b) &= 28 \\ 2a+8b &= 28 \\ a+4b &= 14\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\frac{\begin{align}a+b &= 5 \\ a+4b &= 14 \end{align}}{\begin{align}-3b &= -9 \\ b &= 3 \end{align}}-$
$\begin{align}a+b &= 5 \\ a+3 &= 5 \\ a &= 2 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_9 &= a+8b \\ &= 2+8.3 \\ U_9 &= 26 \end{align}$
Jawaban: B
A. 30
B. 34
C. 38
D. 42
E. 46
$\begin{align}U_n &= S_n-S_{n-1} \\ U_7 &= S_7-S_6 \\ &= (2.7^2+4.7)-(2.6^2+4.6) \\ &= 126-96 \\ U_7 &= 30 \end{align}$
Jawaban: A
A. 38
B. 42
C. 46
D. 50
E. 54
$\begin{align}
U_n &= S_n-S_{n-1} \\ U_{20} &= S_{20}-S_{19} \\ &= (20^2+3.20)-(19^2+3.19) \\ &= 460-418 \\ U_{20} &= 42 \end{align}$
Jawaban: B
A. 49
B. $47\frac{1}{2}$
C. 35
D. $33\frac{1}{2}$
E. 29
$\begin{align}U_n &= S_n-S_{n-1} \\ U_{10} &= S_{10}-S_9 \\ &= \left( \frac{5}{2}.10^2+\frac{3}{2}.10 \right)-\left( \frac{5}{2}.9^2+\frac{3}{2}.9 \right) \\ &= 265-216 \\ U_{10} &= 49 \end{align}$
Jawaban: A
A. 117
B. 120
C. 137
D. 147
E. 160
$U_3=18$, $U_5=24$ maka $S_7$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_3=a+2b &= 18 \\ U_5=a+4b &= 24 \end{align}}{\begin{align}-2b &= -6 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan $a+2b=18$ maka:
$\begin{align}a+2b &= 18 \\ a+2.3 &= 18 \\ a &= 12 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_7 &= \frac{7}{2}(2a+6b) \\ &= \frac{7}{2}(2.12+6.3) \\ &= \frac{7}{2}\times 42 \\ S_7 &= 147 \end{align}$
Jawaban: D
A. 336
B. 672
C. 756
D. 1.344
E. 1.512
Ingat, $U_n=a+(n-1)b$ maka:
$U_7=a+6b=16\,....\,(1)$
$\begin{align}U_3+U_9 &= 24 \\ (a+2b)+(a+8b) &= 24 \\ 2a+10b &= 24 \\ a+5b &= 12\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\frac{\begin{align}a+6b &= 16 \\ a+5b &= 12 \end{align}}{b=4}-$
$\begin{align}a+6b &= 16 \\ a+6.4 &= 16 \\ a &= -8 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{21} &= \frac{21}{2}(2a+20b) \\ &= \frac{21}{2}(2.(-8)+20.4) \\ &= \frac{21}{2}\times 64 \\ S_{21} &= 672 \end{align}$
Jawaban: B
A. 1.535
B. 1.575
C. 1.950
D. 2.000
E. 2.700
30, 34, 38, 42, …. dan $n=25$ maka $S_{25}$ = …
$a=30$
$b=U_2-U_1=34-30=4$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{25} &= \frac{25}{2}(2a+24b) \\ &= \frac{25}{2}(2.30+24.4) \\ &= \frac{25}{2}\times 156 \\ S_{25} &= 1.950 \end{align}$
Jawaban: C
Tata Cara Belajar:
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cek jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cek jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
Soal No. 1
Diberikan tiga suku berurutan deret aritmetika: $2a+b$, $6a+b$, $14a+b$. Nilai $a$ = ….A. $-4$
B. $-2$
C. 0
D. 2
E. 4
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$2a+b$, $6a+b$, $14a+b$
Syarat barisan aritmetika:
$\begin{align}U_2-U_1 &= U_3-U_2 \\ 2U_2 &= U_1+U_3 \\ 2(6a+b) &= 2a+b+14a+b \\ 12a+2b &= 16a+2b \\ 12a-16a &= 2b-2b \\ -4a &= 0 \\ a &= 0 \end{align}$
Jawaban: C
Soal No. 2
Jika diketahui 4 suku pertama dari barisan aritmetika adalah $x$, $y$, $w$, $2y$ maka nilai $\frac{y}{x}$ = ….A. $\frac{1}{4}$
B. $\frac{1}{3}$
C. $\frac{3}{4}$
D. 3
E. 2
Penyelesaian: Lihat/Tutup
Barisan aritmetika: $x$, $y$, $w$, $2y$Syarat barisan aritmetika: $U_2-U_1=U_3-U_2=U_4-U_3$
$\begin{align}U_3-U_2 &= U_4-U_3 \\ 2U_3 &= U_2+U_4 \\ 2w &= y+2y \\ 2w &= 3y \end{align}$
$\begin{align}U_2-U_1 &= U_3-U_2 \\ 2U_2 &= U_1+U_3 \\ 2y &= x+w|\,kedua\,ruas\,\times 2 \\ 4y &= 2x+2w \\ 4y &= 2x+3y \\ 4y-3y &= 2x \\ y &= 2x \end{align}$
Nilai $\frac{y}{x}=\frac{2x}{x}\Leftrightarrow \frac{y}{x}=2$
Jawaban: E
Soal No. 3
Suku ke-25 barisan aritmetika 2, 5, 8, 11, … adalah ….A. 50
B. 52
C. 74
D. 77
E. 78
Penyelesaian: Lihat/Tutup
Barisan aritmetika: 2, 5, 8, 11, …$a=2$
$\begin{align}b &= U_2-U_1 \\ &= 5-2 \\ b &= 3 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{25} &= 2+(25-1).3 \\ &= 2+72 \\ U_{25} &= 74 \end{align}$
Jawaban: C
Soal No. 4
Suku pertama suatu barisan aritmetika adalah 36 sedangkan suku ke-12 sama dengan $-30$. Suku ke-7 barisan tersebut adalah ….A. 12
B. 6
C. 0
D. $-6$
E. $-12$
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$a=36$, $U_{12}=-30$, $U_7$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_{12} &= -30 \\ a+11b &= -30 \\ 36+11b &= -30 \\ 11b &= -30-36 \\ 11b &= -66 \\ b &= -6 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_7 &= a+6b \\ &= 36+6.(-6) \\ &= 36-36 \\ U_7 &= 0 \end{align}$
Jawaban: C
Soal No. 5
Diberikan sebuah deret aritmetika dengan suku kedua adalah 5. Jumlah suku keempat dan keenam adalah 28. Suku kesembilan adalah ….A. 24
B. 25
C. 26
D. 27
E. 28
Penyelesaian: Lihat/Tutup
Ingat, $U_n=a+(n-1)b$ maka:$U_2=5\to a+b=5\,....\,(1)$
$\begin{align}U_4+U_6 &= 28 \\ (a+3b)+(a+5b) &= 28 \\ 2a+8b &= 28 \\ a+4b &= 14\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2) maka:
$\frac{\begin{align}a+b &= 5 \\ a+4b &= 14 \end{align}}{\begin{align}-3b &= -9 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan (1):
$\begin{align}a+b &= 5 \\ a+3 &= 5 \\ a &= 2 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_9 &= a+8b \\ &= 2+8.3 \\ U_9 &= 26 \end{align}$
Jawaban: C
Soal No. 6
Diketahui suku tengah barisan aritmetika adalah 25. Jika beda dan suku ke-5 berturut-turut adalah 4 dan 21, maka jumlah semua suku pada barisan tersebut adalah ….A. 175
B. 189
C. 275
D. 295
E. 375
Penyelesaian: Lihat/Tutup
$U_t=25$, $b=4$, $U_5=21$ maka $S_n$ = …?Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_5 &= 21 \\ a+4b &= 21 \\ a+4.4 &= 21 \\ a+16 &= 21 \\ a &= 21-16 \\ a &= 5 \end{align}$
$\begin{align}U_t &= 25 \\ a+(t-1)b &= 25 \\ 5+(t-1).4 &= 25 \\ 5+4t-4 &= 25 \\ 4t &= 24 \\ t &= 6 \end{align}$
Ingat, $t=\frac{n+1}{2}$ maka:
$\begin{align}\frac{n+1}{2} &= t \\ \frac{n+1}{2} &= 6 \\ n+1 &= 12 \\ n &= 11 \end{align}$
$\begin{align}S_n &= n.U_t \\ S_{11} &= 11\times 25 \\ &= 275 \end{align}$
Jawaban: C
Soal No. 7
Jumlah n suku pertama suatu deret didefinisikan sebagai $S_n=3{{n}^2}-4n$. Jika $U_n$ adalah suku ke-n, maka $U_{10}$ adalah ….A. 43
B. 53
C. 67
D. 147
E. 240
Penyelesaian: Lihat/Tutup
$S_n=3n^2-4n$$\begin{align}U_n &= S_n-S_{n-1} \\ U_{10} &= S_{10}-S_9 \\ &= (3.10^2-4.10)-(3.9^2-4.9) \\ &= (300-40)-(243-36) \\ &= 260-207 \\ U_{10} &= 53 \end{align}$
Jawaban: B
Soal No. 8
Suku ketujuh dan suku kedua barisan artimetika berturut-turut adalah 43 dan 13. Jumlah sepuluh suku pertama deret aritmetika itu adalah ....A. 205
B. 340
C. 410
D. 610
E. 900
Penyelesaian: Lihat/Tutup
Barisan aritmetika: $U_n=a+(n-1)b$$\frac{\begin{align}U_7=a+6b &= 43 \\ U_2=a+b &= 13 \end{align}}{\begin{align}5b &= 30 \\ b &= 6 \end{align}}-$
Substitusi $b=6$ ke persamaan $a+b=13$ maka:
$\begin{align}a+b &= 13 \\ a+6 &= 13 \\ a &= 7 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{10} &= \frac{10}{2}(2.7+(10-1).6) \\ &= 5(14+54) \\ &= 5(68) \\ S_{10} &= 340 \end{align}$
Jawaban: B
Soal No. 9
Jumlah semua bilangan bulat antara 250 dan 1.000 yang habis dibagi 7 adalah ….A. 45.692
B. 54.396
C. 66.661
D. 73.775
E. 80.129
Penyelesaian: Lihat/Tutup
Ingat:$\left\lfloor x \right\rfloor $ = bilangan bulat terbesar yang lebih kecil atau sama dengan $x$.
$\left\lceil x \right\rceil $ = bilangan bulat terkecil yang lebih besar atau sama dengan $x$.
$\begin{align}a &= \left\lfloor \frac{250}{7}+1 \right\rfloor \times 7 \\ &= \left\lfloor 35,71+1 \right\rfloor \times 7 \\ &= \left\lfloor 36,71 \right\rfloor \times 7 \\ &= 36\times 7 \\ a &= 252 \end{align}$
$\begin{align}U_n &= \left\lceil \frac{1.000}{7}-1 \right\rceil \times 7 \\ &= \left\lceil 142,86-1 \right\rceil \times 7 \\ &= \left\lceil 141,86 \right\rceil \times 7 \\ &= 142\times 7 \\ U_n &= 994 \end{align}$
Karena ini adalah deret bilangan yang habis dibagi 7 maka $b=7$
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_n &= 994 \\ a+(n-1)b &= 994 \\ 252+(n-1)7 &= 994 \\ 7(n-1) &= 742 \\ n-1 &= 106 \\ n &= 107 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(a+U_n) \\ S_{107} &= \frac{107}{2}(252+994) \\ &= \frac{107}{2}(1.246) \\ &= 107\times 623 \\ S_{107} &= 66.661 \end{align}$
Jawaban: C
Soal No. 10
Suku ke-n suatu deret aritmetika $U_n=3n-5$. Rumus jumlah n suku pertama deret tersebut adalah ….A. $S_n=\frac{n}{2}(3n-7)$
B. $S_n=\frac{n}{2}(3n-5)$
C. $S_n=\frac{n}{2}(3n-4)$
D. $S_n=\frac{n}{2}(3n-3)$
E. $S_n=\frac{n}{2}(3n-2)$
Penyelesaian: Lihat/Tutup
$U_n=3n-5$ maka $S_n$ = ...?$\begin{align}a &= U_1 \\ &= 3.1-5 \\ a &= -2 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(a+U_n) \\ &= \frac{n}{2}(-2+3n-5) \\ S_n &= \frac{n}{2}(3n-7) \end{align}$
Jawaban: A
Soal No. 11
$\log a$ + $\log a^2$ + $\log a^3$ + … + $\log a^n$ = ….A. $n\log a(n+1)$
B. $n(n+1)\log a$
C. $\frac{1}{2}n\log a(n+1)$
D. $\frac{1}{2}n(n+1)\log a$
E. $\frac{1}{2}n(n-1)\log a$
Penyelesaian: Lihat/Tutup
Cek apakah deret ini merupakan deret aritmetika atau bukan.$\begin{align}U_2-U_1 &= \log a^2-\log a \\ &= 2\log a-\log a \\ U_2-U_1 &= \log a \end{align}$
$\begin{align}U_3-U_2 &= \log a^3-\log a^2 \\ &= 3\log a-2\log a \\ U_3-U_2 &= \log a \end{align}$
Karena $U_2-U_1=U_3-U_2$ maka deret tersebut merupakan deret aritmetika dengan:
$U_1=\log a$ dan $U_n=\log a^n$ maka:
$\begin{align}S_n &= \frac{n}{2}(U_1+U_n) \\ &= \frac{1}{2}n(\log a+\log a^n) \\ &= \frac{n}{2}(\log a+n\log a) \\ S_n &= \frac{1}{2}n(n+1)\log a \end{align}$
Jawaban: D
Soal No. 12
Dari suatu deret aritmetika diketahui $U_6+U_9+U_{12}+U_{15}=20$. Nilai $S_{20}$ = ….A. 50
B. 80
C. 100
D. 200
E. 400
Penyelesaian: Lihat/Tutup
$U_6+U_9+U_{12}+U_{15}=20$ maka $S_{20}= ...?$a+5b$ + $a+8b$ + $a+11b$ + $a+14b$ = 20
$4a+38b=20$
$2a+19b=10$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b \\ S_{20} &= \frac{20}{2}(2a+(20-1)b) \\ &= 10(2a+19b) \\ &= 10.10 \\ S_{20} &= 100 \end{align}$
Jawaban: C
Soal No. 13
Jumlah n suku pertama deret aritmetika adalah $S_n=n^2+\frac{5}{2}n$. Beda dari deret aritmetika tersebut adalah ….A. $-\frac{11}{2}$
B. $-2$
C. 2
D. $\frac{5}{2}$
E. $\frac{11}{2}$
Penyelesaian: Lihat/Tutup
$S_n=n^2+\frac{5}{2}n$ maka $b$ = ...?$\begin{align}U_1 &= S_1 \\ &= 1^2+\frac{5}{2}.1 \\ U_1 &= \frac{7}{2} \end{align}$
$\begin{align}U_n &= S_n-S_{n-1} \\ U_2 &= S_2-S_1 \\ &= \left( 2^2+\frac{5}{2}.2 \right)-\left( 1^2+\frac{5}{2}.1 \right) \\ &= \left( 4+5 \right)-\left( 1+\frac{5}{2} \right) \\ &= 9-\frac{7}{2} \\ U_2 &= \frac{11}{2} \end{align}$
$\begin{align}b &= U_2-U_1 \\ &= \frac{11}{2}-\frac{7}{2} \\ b &= \frac{5}{2} \end{align}$
Jawaban: D
Soal No. 14
Sebuah tali dipotong menjadi lima bagian dan membentuk deret aritmetika. Jika panjang tali terpendek 2 cm dan panjang tali semula adalah 200 cm, maka panjang tali yang ketiga adalah …A. 9
B. 10
C. 19
D. 20
E. 40
Penyelesaian: Lihat/Tutup
Tali dibagi menjadi lima bagian maka $n=5$Tali terpendek = $a$ = 2 cm
Panjang tali semula = $S_5$= 200 cm
Panjang tali ketiga = $U_3$ = …?
Ingat, $S_n=\frac{n}{2}(2a+(n-1)b)$ maka:
$\begin{align}S_5 &= 200 \\ \frac{5}{2}(2.2+(5-1)b) &= 200 \\ 5(4+4b) &= 400 \\ 4+4b &= 80 \\ 4b &= 76 \\ b &= 19 \end{align}$
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_3 &= a+2b \\ &= 2+2.19 \\ U_3 &= 40 \end{align}$
Jawaban: E
Soal No. 15
Sisi-sisi suatu segitiga siku-siku membentuk suatu barisan aritmetik. Jika sisi miringnya 40, maka sisi siku-siku yang terpendek adalah …A. 8
B. 16
C. 20
D. 24
E. 32
Penyelesaian: Lihat/Tutup

$\begin{align}a+2b &= 40 \\ a+b+b &= 40 \\ a+b &= 40-b \end{align}$
$a+2b=40\to a=40-2b$
Karena $a$ adalah salah satu panjang sisi segitiga maka:
$\begin{align}a > 0 \\ 40-2b > 0 \\ -2b > -40 \\ b < 20 \end{align}$
Dengan menggunakan teorema pythagoras maka:
$\begin{align}(a+2b)^2 &= a^2+(a+b)^2 \\ 40^2 &= (40-2b)^2+(40-b)^2 \\ 1600 &= 1600-160b+4b^2+1600-80b+b^2 \\ 0 &= 5b^2-240b+1600 \\ 0 &= b^2-48b+320 \\ 0 &= (b-40)(b-8) \end{align}$
$b-8=0\to b=8$ (memenuhi)
$b-40=0\to b=40$ (tidak memenuhi)
Panjang sisi siku-siku terpendek adalah:
$\begin{align}a &= 40-2b \\ &= 40-2.8 \\ a &= 24 \end{align}$
Jadi, panjang sisi siku-siku terpendek adalah 24 cm.
Cara alternatif:
Jika panjang sisi-sisi segitiga membentuk barisan aritmetika maka ketiga sisinya adalah $3x$, $4x$ dan $5x$ untuk $x > 0$, maka:
Sisi terpanjang = 40
$5x=40\to x=8$
Sisi terpendek = $3x=3.8=24$ cm.
Jawaban: D
Soal No. 16
Tempat duduk pertunjukan film di atur mulai dari depan ke belakang dengan banyak baris di belakang lebih 4 kursi dari baris di depannya. Bila dalam gedung pertunjukan terdapat 15 baris dan baris terdepan ada 20 kursi, maka kapasitas gedung pertunjukan tersebut adalah….. tempat duduk.A. 1.200
B. 800
C. 720
D. 600
E. 300
Penyelesaian: Lihat/Tutup
Barisan aritmetika:Banyak baris di belakang lebih 4 kursi dari baris di depannya maka $b=4$.
Dalam gedung pertunjukan terdapat 15 baris maka $n=15$.
Baris terdepan ada 20 kursi $a=20$
Kapasitas gedung pertunjukan tersebut adalah $S_{15}$ = …?
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{15} &= \frac{15}{2}(2.20+14.4) \\ &= \frac{15}{2}(40+56) \\ &= \frac{15}{2}\times 96 \\ S_{15} &= 720 \end{align}$
Kapasitas gedung pertunjukan tersebut adalah 720 tempat duduk.
Jawaban: C
Soal No. 17
Harminingsih bekerja di perusahaan dengan kontrak selama 10 tahun dengan gaji awal Rp1.600.000,00. setiap tahun Harminingsih mendapat kenaikan gaji berkala sebesar Rp200.000,00. Total seluruh gaji yang diterima Harminingsih hingga menyelesaikan kontrak kerja adalah ….A. Rp25.800.000,00
B. Rp25.200.000,00
C. Rp25.000.000,00
D. Rp18.800.000,00
E. Rp18.000.000,00
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$n$ = 10 tahun
$a$ = Rp1.600.000,00
$b$ = Rp200.000,00
$S_{10}$ = ….
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{10} &= \frac{10}{2}(2(1.600.000)+9.(200.000)) \\ &= 5(3.200.000+1.800.000) \\ &= 5(5.000.000) \\ S_{10} &= 25.000.000 \end{align}$
Jawaban: C
Soal No. 18
Sebuah pabrik memproduksi barang jenis A pada tahun pertama sebesar 1.960 unit. Tiap tahun produksi turun sebesar 120 unit sampai tahun ke-16. Total seluruh produksi yang dicapai sampai tahun ke-16 adalah ...A. 45.760
B. 45.000
C. 16.960
D. 16.000
E. 9.760
Penyelesaian: Lihat/Tutup
$a=1.960$Tiap tahun produksi turun sebesar 120 unit maka $b=-120$.
$S_{16}$ = …?
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{16} &= \frac{16}{2}(2(1.960)+15(-120)) \\ &= 8(3.920-1.800) \\ &= 8\times 2.120 \\ S_{16} &= 16.960 \end{align}$
Jawaban: C
Soal No. 19
Keuntungan seorang pedagang bertambah setiap bulan dengan jumlah yang sama. Jika keuntungan pada bulan pertama sebesar Rp46.000,00 dan pertambahan keuntungan setiap bulan Rp18.000,00 maka jumlah keuntungan sampai bulan ke-12 adalah …A. Rp1.740.000,00
B. Rp1.750.000,00
C. Rp1.840.000,00
D. Rp1.950.000,00
E. Rp2.000.000,00
Penyelesaian: Lihat/Tutup
$a$ = Rp46.000,00$b$ = Rp18.000,00
$S_{12}$ = ….
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{12} &= \frac{12}{2}(2(46.000)+11(18.000)) \\ &= 6(92.000+198.000) \\ &= 6(290.000) \\ S_{12} &= 1.740.000 \end{align}$
Jawaban: A
Soal No. 20
Diketahui lima orang bersaudara dengan selisih umur yang sama. Anak termuda berusia 13 tahun dan yang tertua 33 tahun. Jumlah usia mereka seluruhnya adalah …tahun.A. 112
B. 115
C. 125
D. 130
E. 160
Penyelesaian: Lihat/Tutup
Barisan aritmetika:Usia anak termuda 13 tahun maka $a=13$.
Usia anak tertua 33 tahun maka $U_5=33$.
Jumlah usia mereka = $S_5$ = …?
$\begin{align}S_n &= \frac{n}{2}(a+U_n) \\ S_5 &= \frac{5}{2}(a+U_5) \\ &= \frac{5}{2}(13+33) \\ &= 5\times 23 \\ S_5 &= 115 \end{align}$
Jadi, jumlah usia mereka adalah 115 tahun.
Jawaban: B
Soal No. 21
Barisan $(3k+12)$, $(2k+16)$, $(44-k)$, … merupakan tiga suku pertama suatu barisan aritmetika. Formula suku ke-n barisan itu adalah ….A. 8(7 + n)
B. 4(7 + n)
C. 8(7 – n)
D. 4(7 – n)
E. 7(8 – 4n)
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$(3k+12)$, $(2k+16)$, $(44-k)$, …
Syarat barisan aritmetika:
$\begin{align}U_2-U_1 &= U_3-U_2 \\ 2U_2 &= U_1+U_3 \\ 2(2k+16) &= 3k+12+44-k \\ 4k+32 &= 2k+56 \\ 4k-2k &= 56-32 \\ 2k &= 24 \\ k &= 12 \end{align}$
$\begin{align}U_1 &= 3k+12 \\ &= 3.12+12 \\ U_1 &= 48=a \end{align}$
$\begin{align}U_2 &= 2k+16 \\ &= 2.12+16 \\ U_2 &= 40 \end{align}$
$\begin{align}b &= U_2-U_1 \\ &= 40-48 \\ b &= -8 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ &= 48+(n-1).(-8) \\ &= 48-8n+8 \\ &= 56-8n \\ U_n &= 8(7-n) \end{align}$
Jawaban: C
Soal No. 22
Suku ke-4 suatu barisan aritmetika adalah 56, sedangkan suku ke-9 sama dengan 26. Beda barisan tersebut adalah ….A. $-6$
B. $-5$
C. 5
D. 6
E. 30
Penyelesaian: Lihat/Tutup
$U_4=56$, $U_9=26$, $b$ = …Barisan aritmetika: $U_n=a+(n-1)b$
$\frac{\begin{align}U_4 = a+3b &= 56 \\ U_9 = a+8b &= 26 \end{align}}{\begin{align}-5b &= 30 \\ b &= -6 \end{align}}-$
Jadi, beda barisan tersebut adalah $-6$.
Jawaban: A
Soal No. 23
Dari suatu barisan aritmetika diketahui suku ke-3 dan suku ke-10 berturut-turut adalah $-5$ dan 51. Suku ke-28 barisan tersebut adalah ….A. 171
B. 179
C. 187
D. 195
E. 203
Penyelesaian: Lihat/Tutup
$U_3=-5$, $U_{10}=51$, $U_{28}$ = ….Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_3=a+2b &= -5 \\ U_10=a+9b &= 51 \end{align}}{\begin{align}-7b &= -56 \\ b &= 8 \end{align}}-$
Substitusi $b=8$ ke persamaan $a+2b=-5$ maka:
$\begin{align}a+2b &= -5 \\ a+2.8 &= -5 \\ a+16 &= -5 \\ a &= -5-16 \\ a &= -21 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{28} &= a+27b \\ &= -21+27.8 \\ &= -21+216 \\ U_{28} &= 195 \end{align}$
Jawaban: D
Soal No. 24
Diketahui jumlah suku ke-2 dan ke-4 dari barisan aritmetika adalah 26. Dan selisih suku ke-8 dan ke-5 adalah 9. Suku ke-10 dari barisan aritmetika tersebut adalah ….A. 18
B. 24
C. 28
D. 34
E. 43
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$U_2+U_4=26$, $U_8-U_5=9$, $U_{10}$ = ….
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_2+U_4 &= 26 \\ (a+b)+(a+3b) &= 26 \\ 2a+4b &= 26 \\ a+2b &= 13 \end{align}$
$\begin{align}U_8-U_5 &= 9 \\ (a+7b)-(a+4b) &= 9 \\ 3b &= 9 \\ b &= 3 \end{align}$
Substitusi ke persamaan $a+2b=13$ maka:
$\begin{align}a+2b &= 13 \\ a+2.3 &= 13 \\ a+6 &= 13 \\ a &= 7 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{10} &= a+9b \\ &= 7+9.3 \\ &= 7+27 \\ U_{10} &= 34 \end{align}$
Jawaban: D
Soal No. 25
Ukuran sisi sebuah segitiga siku-siku membentuk suatu barisan aritmetika. Jika luas segitiga itu 54, maka kelilingnya sama dengan …A. 32
B. 36
C. 40
D. 44
E. 48
Penyelesaian: Lihat/Tutup

Dengan menggunakan teorema pythagoras maka:
$\begin{align}(a+2b)^2 &= a^2+(a+b)^2 \\ a^2+4ab+4b^2 &= a^2+a^2+2ab+b^2 \\ a^2-2ab-3b^2 &= 0 \\ a^2+ab-3ab-3b^2 &= 0 \\ a(a+b)-3b(a+b) &= 0 \\ (a+b)(a-3b) &= 0 \end{align}$
Perhatikan, $a+b > 0$ maka $a-3b=0\Leftrightarrow a=3b$
Luas segitiga = 54 maka:
$\begin{align}L &= 54 \\ \frac{1}{2}a(a+b) &= 54 \\ a(a+b) &= 108 \\ 3b(3b+b) &= 108 \\ 12b^2 &= 0 \\ b^2 &= 9 \\ b &= 3 \end{align}$
$a=3b\Leftrightarrow a=3.3=9$
$\begin{align}K &= a+(a+b)+(a+2b) \\ &= 3a+3b \\ &= 3.9+3.3 \\ K &= 36 \end{align}$
Jadi, keliling segitiga tersebut adalah 36 cm.
Cara alternatif:
Jika panjang sisi-sisi segitiga membentuk barisan aritmetika maka ketiga sisinya adalah $3x$, $4x$ dan $5x$ untuk $x>0$.
$\begin{align}L &= 54 \\ \frac{1}{2}.3x.4x &= 54 \\ 6x^2 &= 54 \\ x^2 &= 9 \\ x &= 3 \end{align}$
$\begin{align}K &= 3x+4x+5x \\ &= 12x \\ &= 12.3 \\ K &= 36 \end{align}$
Jawaban: B
Soal No. 26
Barisan bilangan aritmetika terdiri dari 21 suku. Suku tengah barisan tersebut adalah 52, sedangkan $U_3+U_5+U_{15}=106$. suku ke-7 barisan tersebut adalah ….A. 27
B. 30
C. 32
D. 35
E. 41
Penyelesaian: Lihat/Tutup
Barisan aritmetika: $n=21$, $U_t=52$, $U_3+U_5+U_{15}=106$, $U_7$ = ….$t=\frac{n+1}{2}=\frac{21+1}{2}\Leftrightarrow t=11$
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_t &= 52 \\ U_{11} &= 52 \\ a+10b &= 52\,....\,(1) \end{align}$
$\begin{align}U_3+U_5+U_{15} &= 106 \\ (a+2b)+(a+4b)+(a+14b) &= 106 \\ 3a+20b &= 106\,....(2) \end{align}$
Eliminasi $b$ dari persamaan (2) dan (1):
$\left. \begin{align}3a+20b &= 106 \\ a+10b &= 52 \end{align} \right|\begin{matrix} \times 1 \\ \times 2 \\ \end{matrix}$
$\frac{\begin{align}3a+20b &= 106 \\ 2a+20b &= 104 \\ \end{align}}{a=2}-$
Substitusi $a=2$ ke persamaan (1):
$\begin{align}a+10b &= 52 \\ 2+10b &= 52 \\ 10b &= 50 \\ b &= 5 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_7 &= a+6b \\ &= 2+6.5 \\ U_7 &= 32 \end{align}$
Jawaban: C
Soal No. 27
Seorang ayah membagikan uang sebesar Rp100.000,00 kepada 4 orang anaknya. Makin muda usia anak, makin kecil uang yang diterima. Jika selisih yang diterima oleh setiap dua anak yang usianya berdekatan adalah Rp5.000,00 dan si sulung menerima uang paling banyak, maka jumlah uang yang diterima oleh si bungsu adalah … A. Rp15.000,00
B. Rp17.500,00
C. Rp20.000,00
D. Rp22.500,00
E. Rp25.000,00
Penyelesaian: Lihat/Tutup
$S_4=100.000$$a$ = jumlah uang yang diterima anak pertama dan $b=-5.000$
Ingat, $S_n=\frac{n}{2}(2a+(n-1)b)$ maka:
$\begin{align}S_4 &= 100.000 \\ \frac{4}{2}(2a+3b) &= 100.000 \\ 2a+3b &= 50.000 \\ 2a+3(-5.000) &= 50.000 \\ 2a-15.000 &= 50.000 \\ 2a &= 65.000 \\ a &= 32.500 \end{align}$
Si bungsu = anak ke-4.
Jumlah uang yang diterima oleh si bungsu adalah $U_4$.
$\begin{align}U_n &= a+(n-1)b \\ U_4 &= a+3b \\ &= 32.500+3(-5.000) \\ &= 32.500-15.000 \\ U_4 &= 17.500 \end{align}$
Jawaban: B
Soal No. 28
Dari barisan aritmetika diketahui $U_2=7$dan $U_5=-2$ maka $S_{10}$ = ….A. $-35$
B. $-25$
C. 0
D. 25
E. 35
Penyelesaian: Lihat/Tutup
Barisan aritmetika: $U_n=a+(n-1)b$$\frac{\begin{align}U_2=a+b &= 7\, \\ U_5=a+4b &= -2 \\ \end{align}}{\begin{align}-3b &= 9 \\ b &= -3 \end{align}}-$
Substitusi $b=-3$ ke persamaan $a+b=7$ maka:
$\begin{align}a+b &= 7 \\ a+(-3) &= 7 \\ a &= 10 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{10} &= \frac{10}{2}(2a+9b) \\ &= 5(2.10+9.(-3)) \\ &= 5(20-27) \\ S_{10} &= -35 \end{align}$
Jawaban: A
Soal No. 29
Jumlah n suku pertama suatu deret aritmetika dinyatakan dengan rumus $S_n=2n^2-n$. Suku kesepuluh deret tersebut adalah ….A. 35
B. 36
C. 37
D. 38
E. 39
Penyelesaian: Lihat/Tutup
$S_n=2n^2-n$, $U_{10}$$\begin{align}U_n &= S_n-S_{n-1} \\ U_{10} &= S_{10}-S_9 \\ &= (2.10^2-10)-(2.9^2-9) \\ &= 190-153 \\ U_{10} &= 37 \end{align}$
Jawaban: C
Soal No. 30
Suatu perusahaan pakaian dapat menghasilkan 4.000 buah pada awal produksi. Pada bulan berikutnya produksi dapat ditingkatkan menjadi 4.050. Bila kemajuan tetap, maka jumlah produksi dalam 1 tahun ada … buahA. 45.500
B. 48.000
C. 50.500
D. 51.300
E. 55.500
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$U_n$ = jumlah produksi dalam bulan ke-n
$U_1=4.000=a$
$U_2=4.050$
$S_{12}$ = …?
$\begin{align}b &= U_2-U_1 \\ &= 4.050-4.000 \\ b &= 50 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{12} &= \frac{12}{2}(2a+11b) \\ &= 6(2\times 4.000+11\times 50) \\ &= 6\times 8.550 \\ S_{12} &= 51.300 \end{align}$
Jawaban: D
Soal No. 31
Seorang penjual daging pada bulan Januari menjual 120 kg, bulan Februari 130 kg, Maret dan seterusnya selama 10 bulan selalu bertambah 10 kg dari bulan sebelumnya. Jumlah daging yang terjual selama 10 bulan adalah … kgA. 1.050
B. 1.200
C. 1.350
D. 1.650
E. 1.750
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$a=120$, $b=10$, $S_{10}$ = ….
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{10} &= \frac{10}{2}(2a+11b) \\ &= 5(2\times 120+11\times 10) \\ &= 5\times 350 \\ S_{10} &= 1.750 \end{align}$
Jawaban: E
Soal No. 32
Diketahui suku ke-3 dan ke-7 barisan aritmetika berturut-turut 10 dan 26. Suku ke-10 adalah ….A. 38
B. 40
C. 42
D. 44
E. 46
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$U_3=10$, $U_7=26$, $U_{10}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_3=a+2b &= 10 \\ U_7=a+6b &= 26 \\ \end{align}}{\begin{align}-4b &= -16 \\ b &= 4 \end{align}}-$
Substitusi $b=4$ ke persamaan $a+2b=10$ maka:
$\begin{align}a+2b &= 10 \\ a+2.4 &= 10 \\ a &= 2 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{10} &= a+9b \\ &= 2+9.4 \\ U_{10} &= 38 \end{align}$
Jawaban: A
Soal No. 33
Diketahui suku ke-3 dan suku ke-8 suatu barisan aritmetika berturut-turut 7 dan 27. Suku ke-20 barisan tersebut adalah ….A. 77
B. 76
C. 75
D. 67
E. 66
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$U_3=7$, $U_8=27$, $U_{20}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_3=a+2b &= 7 \\ U_8=a+7b &= 27 \\ \end{align}}{\begin{align}-5b &= -20 \\ b &= 4 \end{align}}-$
Substitusi $b=4$ ke persamaan $a+2b=7$ maka:
$\begin{align}a+2b &= 7 \\ a+2.4 &= 7 \\ a &= -1 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{20} &= a+19b \\ &= -1+19.4 \\ U_{20} &= 75 \end{align}$
Jawaban: C
Soal No. 34
Suku keempat dan suku ketujuh suatu barisan aritmetika berturut-turut adalah 5 dan 14. Suku kelima belas barisan tersebut adalah …A. 35
B. 38
C. 39
D. 40
E. 42
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$U_4=5$, $U_7=14$, $U_{15}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_4=a+3b &= 5 \\ U_7=a+6b &= 14 \\ \end{align}}{\begin{align}-3b &= -9 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan $a+3b=5$ maka:
$\begin{align}a+3b &= 5 \\ a+3.3 &= 5 \\ a &= -4 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{15} &= a+14b \\ &= -4+14\times 3 \\ U_{15} &= 38 \end{align}$
Jawaban: B
Soal No. 35
Rini membuat kue yang dijualnya di toko. Hari pertama ia membuat 20 kue, hari kedua 22 kue, dan seterusnya. Setiap hari banyak kue yang dibuat bertambah 2 dibanding hari sebelumnya. Kue-kue itu selalu habis terjual. Jika setiap kue menghasilkan keuntungan Rp1.000,00, maka keuntungan Rini dalam 31 hari pertama adalah …A. Rp1.470.000,00
B. Rp1.550.000,00
C. Rp1.632.000,00
D. Rp1.650.000,00
E. Rp1.675.000,00
Penyelesaian: Lihat/Tutup
Karena pertambahan kue yang dibuat tetap setiap harinya, maka masalah ini merupakan masalah barisan aritmetika:$U_n$ = banyaknya kue yang dibuat pada hari ke-n.
$U_1=20=a$ dan $U_2=22$
Keuntungan = Rp1.000,00/kue.
Keuntungan Rini daam 31 hari pertama adalah 1000 x Jumlah kue yang dibuat selama 31 hari pertama = $1.000\times S_{31}$ = …
$b=U_2-U_1=22-20\Leftrightarrow b=2$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{31} &= \frac{31}{2}(2a+30b) \\ &= \frac{31}{2}(2\times 20+30\times 2) \\ &= \frac{31}{2}\times 100 \\ S_{31} &= 15.500 \end{align}$
Keuntungan Rini selama 31 hari pertama adalah $1.000\times S_{31}$ = $1.000\times 15.500$ = 15.500.000,00.
Jawaban: B
Soal No. 36
Seseorang mempunyai sejumlah uang yang akan diambil tiap bulan yang besarnya mengikuti aturan barisan aritmetika. Pada bulan pertama diambil Rp1.000.000,00, bulan kedua Rp925.000,00, bulan ketiga Rp850.000,00, demikian seterusnya. Jumlah seluruh uang yang telah diambil selama 12 bulan pertama adalah …A. Rp6.750.000,00
B. Rp7.050.000,00
C. Rp7.175.000,00
D. Rp7.225.000,00
E. Rp7.300.000,00
Penyelesaian: Lihat/Tutup
$U_1$ = Rp1.000.000,00 = $a$$U_2$ = Rp925.000,00
$\begin{align}b &= U_2-U_1 \\ &= 925.000-1.000.000 \\ b &= -75.000 \end{align}$
Jumlah seluruh uang yang telah diambil selama 12 bulan pertama adalah $S_{12}$.
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{12} &= \frac{12}{2}(2a+11b) \\ &= 6(2(1.000.000)+11(-75.000)) \\ &= 6(2.000.000-825.000) \\ &= 6(1.175.000) \\ S_{12} &= 7.050.000 \end{align}$
Jawaban: B
Soal No. 37
Rumus jumlah n suku pertama suatu deret aritmetika adalah $S_n=2n^2-12n$. Suku ke-4 deret tersebut adalah …A. 2
B. 6
C. 10
D. 14
E. 18
Penyelesaian: Lihat/Tutup
$S_n=2n^2-12n$$\begin{align}U_n &= S_n-S_{n-1} \\ U_4 &= S_4-S_3 \\ &= (2.4^2-12.4)-(2.3^2-12.3) \\ &= -16-(-18) \\ U_4 &= 2 \end{align}$
Jawaban: A
Soal No. 38
Dari suatu barisan aritmetika diketahui suku ke-5 adalah 22 dan suku ke-12 adalah 57. Suku ke-15 barisan ini adalah …A. 62
B. 68
C. 72
D. 74
E. 76
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$U_5=22$, $U_{12}=57$, $U_{15}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_5=a+4b &= 22 \\ U_{12}=a+11b &= 57 \end{align}}{\begin{align}-7b &= -35 \\ b &= 5 \end{align}}-$
Substitusi $b=5$ ke persamaan $a+4b=22$ maka:
$\begin{align}a+4b &= 22 \\ a+4.5 &= 22 \\ a &= 2 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{15} &= a+14b \\ &= 2+14.5 \\ U_{15} &= 72 \end{align}$
Jawaban: C
Soal No. 39
Suku pertama dan suku kelima suatu barisan aritmetika berturut-turut adalah 2 dan 10, jumlah dua puluh suku pertama barisan tersebut adalah …A. 382
B. 395
C. 400
D. 420
E. 435
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$a=2$, $U_5=10$, $S_{20}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_5 &= 10 \\ a+4b &= 10 \\ 2+4b &= 10 \\ 4b &= 8 \\ b &= 2 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{20} &= \frac{20}{2}(2a+19b) \\ &= 10(2a+19b) \\ &= 10(2.2+19.2) \\ &= 10(4+38) \\ S_{20} &= 420 \end{align}$
Jawaban: D
Soal No. 40
Rumus jumlah n suku pertama deret aritmetika adalah $S_n=6n^2-3n$. Suku ketujuh dari deret tersebut adalah ….A. 39
B. 45
C. 75
D. 78
E. 87
Penyelesaian: Lihat/Tutup
$S_n=6n^2-3n$ maka $U_7$ = ...?$\begin{align}U_n &= S_n-S_{n-1} \\ U_7 &= S_7-S_6 \\ &= (6.7^2-3.7)-(6.6^2-3.6) \\ &= 273-198 \\ U_7 &= 75 \end{align}$
Jawaban: C
Soal No. 41
Suku ke-4 dan ke-9 suatu barisan aritmetika berturut-turut adalah 110 dan 150. Suku ke-30 barisan aritmetika tersebut adalah …A. 308
B. 318
C. 326
D. 344
E. 354
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$U_4=110$, $U_9=150$, $U_{30}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_4=a+3b &= 110 \\ U_9=a+8b &= 150 \end{align}}{\begin{align}-5b &= -40 \\ b &= 8 \end{align}}-$
Substitusi $b=8$ ke persamaan $a+3b=110$ maka:
$\begin{align}a+3b &= 110 \\ a+3.8 &= 110 \\ a+24 &= 110 \\ a &= 86 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{30} &= a+29b \\ &= 86+29\times 8 \\ U_{30} &= 318 \end{align}$
Jawaban: B
Soal No. 42
Suku ke-6 dan ke-12 suatu barisan aritmetika berturut-turut adalah 35 dan 65. Suku ke-52 barisan aritmetika tersebut adalah …A. 245
B. 255
C. 265
D. 285
E. 355
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$U_6=35$, $U_{12}=65$, $U_{52}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_6=a+5b &= 35 \\ U_{12}=a+11b &= 65 \end{align}}{\begin{align}-6b &= -30 \\ b &= 5 \end{align}}-$
Substitusi $b=5$ ke persamaan $a+5b=35$ maka:
$\begin{align}a+5b &= 35 \\ a+5.5 &= 35 \\ a &= 10 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{52} &= a+51b \\ &= 10+51.5 \\ U_{52} &= 265 \end{align}$
Jawaban: C
Soal No. 43
Diketahui suku ke-3 deret aritmetika sama dengan 9, jumlah suku ke-5 dan ke-7 sama dengan 36. Suku ke-12 adalah ....A. 28
B. 32
C. 36
D. 40
E. 42
Penyelesaian: Lihat/Tutup
Deret aritmetika:$U_3=9$, $U_5+U_7=36$, $U_{12}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$U_3=a+2b=9\,....\,(1)$
$\begin{align}U_5+U_7 &= 36 \\ (a+4b)+(a+6b) &= 36 \\ 2a+10b &= 36 \\ a+5b &= 18\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\frac{\begin{align}a+2b &= 9 \\ a+5b &= 18 \end{align}}{\begin{align}-3b &= -9 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan (1):
$\begin{align}a+2b &= 9 \\ a+2.3 &= 9 \\ a &= 3 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{12} &= a+11b \\ &= 3+11.3 \\ U_{12} &= 36 \end{align}$
Jawaban: C
Soal No. 44
Diketahui barisan aritmetika dengan Un adalah suku ke-n. Jika $U_2+U_{15}+U_{40}=165$, maka $U_{19}$ = …A. 10
B. 19
C. 28,5
D. 55
E. 82,5
Penyelesaian: Lihat/Tutup
Ingat, $U_n=a+(n-1)b$ maka:$\begin{align}U_2+U_{15}+U_{40} &= 165 \\ (a+b)+(a+14b)+(a+39b) &= 165 \\ 3a+54b &= 165 \\ a+18b &= 55 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{19} &= a+18b \\ &= 55 \end{align}$
Jawaban: D
Soal No. 45
Jumlah n suku pertama deret aritmetika dinyatakan dengan $S_n=n^2+5n$. Suku ke-20 dari deret aritmetika tersebut adalah …A. 44
B. 42
C. 40
D. 38
E. 36
Penyelesaian: Lihat/Tutup
$S_n=n^2+5n$, $U_{20}$ = …$\begin{align}U_n &= S_n-S_{n-1} \\ U_{20} &= S_{20}-S_{19} \\ &= (20^2+5.20)-(19^2+5.19) \\ &= 500-456 \\ U_{20} &= 44 \end{align}$
Jawaban: A
Soal No. 46
Diketahui barisan aritmetika dengan suku ketiga 8 dan suku kelima 12. Jumlah delapan suku pertama deret tersebut adalah ...A. 176
B. 128
C. 88
D. 64
E. 18
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$U_3=8$, $U_5=12$ maka $S_8$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_3=a+2b &= 8 \\ U_5=a+4b &= 12 \end{align}}{\begin{align}-2b &= -4 \\ b &= 2 \end{align}}-$
Substitusi $b=2$ ke persamaan $a+2b=8$ maka:
$\begin{align}a+2b &= 8 \\ a+2.2 &= 8 \\ a &= 4 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_8 &= \frac{8}{2}(2a+7b) \\ &= 4(2.4+7.2) \\ S_8 &= 88 \end{align}$
Jawaban: C
Soal No. 47
Dalam barisan aritmetika diketahui $U_{11}+U_{17}=84$ dan $U_6+U_7=39$. Nilai suku ke-50 adalah ....A. 150
B. 147
C. 146
D. 145
E. 137
Penyelesaian: Lihat/Tutup
Barisan aritmetika:$U_{11}+U_{17}=84$, $U_6+U_7=39$ maka $U_{50}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\begin{align}U_{11}+U_{17} &= 84 \\ (a+10b)+(a+16b) &= 84 \\ 2a+26b &= 84\,....\,(1) \end{align}$
$\begin{align}U_6+U_7 &= 39 \\ (a+5b)+(a+6b) &= 39 \\ 2a+11b &= 39\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\frac{\begin{align}2a+26b &= 84 \\ 2a+11b &= 39 \end{align}}{\begin{align}15b &= 45 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan (2):
$\begin{align}2a+11b &= 39 \\ 2a+11.3 &= 39 \\ 2a+33 &= 39 \\ 2a &= 6 \\ a &= 3 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_{50} &= a+49b \\ &= 3+49.3 \\ U_{50} &= 150 \end{align}$
Jawaban: A
Soal No. 48
Jumlah n suku pertama barisan aritmetika dinyatakan dengan $S_n=\frac{3n^2+n}{2}$. Beda dari barisan aritmetika tersebut adalah ....A. 2
B. 3
C. 4
D. 5
E. 6
Penyelesaian: Lihat/Tutup
$S_n=\frac{3n^2+n}{2}$$\begin{align}U_n &= S_n-S_{n-1} \\ U_2 &= S_2-S_1 \\ &= \frac{3.2^2+2}{2}-\frac{3.1^2+1}{2} \\ &= 7-2 \\ U_2 &= 5 \end{align}$
$\begin{align}U_1 &= S_1 \\ &= \frac{3.1^2+1}{2} \\ U_1 &= 2 \end{align}$
$b=U_2-U_1=5-2\Leftrightarrow b=3$
Jawaban: B
Soal No. 49
Suku ke-5 sebuah deret aritmetika adalah 11 dan jumlah nilai suku ke-8 dengan suku ke-12 sama dengan 52. Jumlah 8 suku yang pertama deret itu adalah ….A. 68
B. 72
C. 76
D. 80
E. 84
Penyelesaian: Lihat/Tutup
Deret aritmetika:$U_5=11$, $U_8+U_{12}=52$ maka $S_8$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$U_5=a+4b=11\,....\,(1)$
$\begin{align}U_8+U_{12} &= 52 \\ (a+7b)+(a+11b) &= 52 \\ 2a+18b &= 52 \\ a+9b &= 26\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\frac{\begin{align}a+4b &= 11 \\ a+9b &= 26 \end{align}}{\begin{align}-5b &= -15 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan (1):
$\begin{align}a+4b &= 11 \\ a+4.3 &= 11 \\ a &= -1 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_8 &= \frac{8}{2}(2a+7b) \\ &= 4(2.(-1)+7.3) \\ &= 4\times 19 \\ S_8 &= 76 \end{align}$
Jawaban: C
Soal No. 50
Dari suatu deret aritmetika diketahui suku ke-6 adalah 17 dan suku ke-10 adalah 33. Jumlah tiga puluh suku pertama deret itu adalah….A. 1.650
B. 1.710
C. 3.300
D. 4.280
E. 5.300
Penyelesaian: Lihat/Tutup
Deret aritmetika:$U_6=17$, $U_{10}=33$ maka $S_{30}$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_6=a+5b &= 17 \\ U_{10}=a+9b &= 33 \end{align}}{\begin{align}-4b &= -16 \\ b &= 4 \end{align}}-$
Substitusi $b=4$ ke persamaan $a+5b=17$ maka:
$\begin{align}a+5b &= 17 \\ a+5.4 &= 17 \\ a &= -3 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{30} &= \frac{30}{2}(2a+29b) \\ &= 15(2.(-3)+29.4) \\ &= 15\times 110 \\ S_{30} &= 1.650 \end{align}$
Jawaban: A
Soal No. 51
Diketahui deret aritmetika dengan suku ke-7 adalah 16 dan suku ke-5 adalah 10. Jumlah 6 suku pertama dari deret tersebut adalah …A. $-24$
B. $-12$
C. 33
D. 39
E. 66
Penyelesaian: Lihat/Tutup
Deret aritmetika:$U_7=16$, $U_5=10$ maka $S_6$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_7=a+6b &= 16 \\ U_5=a+4b &= 10 \end{align}}{\begin{align}2b &= 6 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan $a+4b=10$ maka:
$\begin{align}a+4b &= 10 \\ a+4.3 &= 10 \\ a &= -2 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_6 &= \frac{6}{2}(2a+5b) \\ &= 3(2.(-2)+5.3) \\ &= 3(-4+15) \\ &= 3\times 11 \\ S_6 &= 33 \end{align}$
Jawaban: C
Soal No. 52
Rumus jumlah n suku pertama suatu deret aritmetika adalah $S_n=3n^2+19n$ . Suku ke-4 deret tersebut adalah …A. 30
B. 34
C. 40
D. 54
E. 84
Penyelesaian: Lihat/Tutup
$S_n=3n^2+19n$ maka $U_4$ = …$\begin{align}U_n &= S_n-S_{n-1} \\ U_4 &= S_4-S_3 \\ &= (3.4^2+19.4)-(3.3^2+19.3) \\ &= 124-84 \\ U_4 &= 40 \end{align}$
Jawaban: C
Soal No. 53
Diketahui jumlah n suku pertma deret aritmetika adalah $S_n=3n-4n^2$. Suku ke-8 adalah …A. $-57$
B. $-56$
C. $-55$
D. $-53$
E. $-48$
Penyelesaian: Lihat/Tutup
$S_n=3n-4n^2$, $U_8$ = …$\begin{align}U_n &= S_n-S_{n-1} \\ U_8 &= S_8-S_7 \\ &= (3.8-4.8^2)-(3.7-4.7^2) \\ &= -232-(-175) \\ U_8 &= -57 \end{align}$
Jawaban: A
Soal No. 54
Diketahui suku ke-2 deret aritmetika sama dengan 5, jumlah suku ke-4 dan ke-6 sama dengan 28. Suku ke-9 adalah ....A. 20
B. 26
C. 36
D. 40
E. 42
Penyelesaian: Lihat/Tutup
Deret aritmetika:$U_2=5$, $U_4+U_6=28$ maka $U_9$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$U_2=a+b=5\,....\,(1)$
$\begin{align}U_4+U_6 &= 28 \\ (a+3b)+(a+5b) &= 28 \\ 2a+8b &= 28 \\ a+4b &= 14\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\frac{\begin{align}a+b &= 5 \\ a+4b &= 14 \end{align}}{\begin{align}-3b &= -9 \\ b &= 3 \end{align}}-$
$\begin{align}a+b &= 5 \\ a+3 &= 5 \\ a &= 2 \end{align}$
$\begin{align}U_n &= a+(n-1)b \\ U_9 &= a+8b \\ &= 2+8.3 \\ U_9 &= 26 \end{align}$
Jawaban: B
Soal No. 55
Jumlah n suku pertama deret aritmetika dinyatakan dengan $S_n=2n^2+4n$, Suku ke-9 dari deret aritmetika tersebut adalah ...A. 30
B. 34
C. 38
D. 42
E. 46
Penyelesaian: Lihat/Tutup
$S_n=2n^2+4n$, $U_9$ = …$\begin{align}U_n &= S_n-S_{n-1} \\ U_7 &= S_7-S_6 \\ &= (2.7^2+4.7)-(2.6^2+4.6) \\ &= 126-96 \\ U_7 &= 30 \end{align}$
Jawaban: A
Soal No. 56
Jumlah n suku pertama deret aritmetika dinyatakan dengan $S_n=n^2+3n$. Suku ke-20 deret tersebut adalah ….A. 38
B. 42
C. 46
D. 50
E. 54
Penyelesaian: Lihat/Tutup
$S_n=n^2+3n$ maka $U_{20}$ = …$\begin{align}
U_n &= S_n-S_{n-1} \\ U_{20} &= S_{20}-S_{19} \\ &= (20^2+3.20)-(19^2+3.19) \\ &= 460-418 \\ U_{20} &= 42 \end{align}$
Jawaban: B
Soal No. 57
Jumlah n suku pertama deret aritmetika dinyatakan dengan $S_n=\frac{5}{2}n^2+\frac{3}{2}n$. Suku ke-10 dari deret aritmetika tersebut adalah ….A. 49
B. $47\frac{1}{2}$
C. 35
D. $33\frac{1}{2}$
E. 29
Penyelesaian: Lihat/Tutup
$S_n=\frac{5}{2}n^2+\frac{3}{2}n$ maka $U_{10}$ = …$\begin{align}U_n &= S_n-S_{n-1} \\ U_{10} &= S_{10}-S_9 \\ &= \left( \frac{5}{2}.10^2+\frac{3}{2}.10 \right)-\left( \frac{5}{2}.9^2+\frac{3}{2}.9 \right) \\ &= 265-216 \\ U_{10} &= 49 \end{align}$
Jawaban: A
Soal No. 58
Diketahui suku ketiga dan suku kelima dari deret aritmetika berturut-turut adalah 18 dan 24. Jumlah tujuh suku pertama deret tersebut adalah …A. 117
B. 120
C. 137
D. 147
E. 160
Penyelesaian: Lihat/Tutup
Deret aritmetika:$U_3=18$, $U_5=24$ maka $S_7$ = …
Ingat, $U_n=a+(n-1)b$ maka:
$\frac{\begin{align}U_3=a+2b &= 18 \\ U_5=a+4b &= 24 \end{align}}{\begin{align}-2b &= -6 \\ b &= 3 \end{align}}-$
Substitusi $b=3$ ke persamaan $a+2b=18$ maka:
$\begin{align}a+2b &= 18 \\ a+2.3 &= 18 \\ a &= 12 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_7 &= \frac{7}{2}(2a+6b) \\ &= \frac{7}{2}(2.12+6.3) \\ &= \frac{7}{2}\times 42 \\ S_7 &= 147 \end{align}$
Jawaban: D
Soal No. 59
Diketahui suatu barisan aritmetika, $U_n$ menyatakan suku ke-n. Jika $U_7=16$ dan $U_3+U_9=24$, maka jumlah 21 suku pertama dari deret aritmetika tersebut adalah …A. 336
B. 672
C. 756
D. 1.344
E. 1.512
Penyelesaian: Lihat/Tutup
$U_7=16$, $U_3+U_9=24$ maka $S_{21}$ = …Ingat, $U_n=a+(n-1)b$ maka:
$U_7=a+6b=16\,....\,(1)$
$\begin{align}U_3+U_9 &= 24 \\ (a+2b)+(a+8b) &= 24 \\ 2a+10b &= 24 \\ a+5b &= 12\,....\,(2) \end{align}$
Eliminasi $a$ dari persamaan (1) dan (2):
$\frac{\begin{align}a+6b &= 16 \\ a+5b &= 12 \end{align}}{b=4}-$
$\begin{align}a+6b &= 16 \\ a+6.4 &= 16 \\ a &= -8 \end{align}$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{21} &= \frac{21}{2}(2a+20b) \\ &= \frac{21}{2}(2.(-8)+20.4) \\ &= \frac{21}{2}\times 64 \\ S_{21} &= 672 \end{align}$
Jawaban: B
Soal No. 60
Suatu ruang pertunjukan memiiliki 25 baris kursi. Terdapat 30 kursi pada baris pertama, 34 kursi pada baris kedua, 38 kursi di baris ketiga, 42 kursi pada baris keempat dan seterusnya. Jumlah kursi yang ada dalam ruang pertunjukan adalah … buah.A. 1.535
B. 1.575
C. 1.950
D. 2.000
E. 2.700
Penyelesaian: Lihat/Tutup
Barisan aritmetika:30, 34, 38, 42, …. dan $n=25$ maka $S_{25}$ = …
$a=30$
$b=U_2-U_1=34-30=4$
$\begin{align}S_n &= \frac{n}{2}(2a+(n-1)b) \\ S_{25} &= \frac{25}{2}(2a+24b) \\ &= \frac{25}{2}(2.30+24.4) \\ &= \frac{25}{2}\times 156 \\ S_{25} &= 1.950 \end{align}$
Jawaban: C

Post a Comment for "Soal Barisan dan Deret Aritmetika Pembahasan"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.