Soal Deret Geometri Tak Hingga dan Pembahasan
Hallo...! Pengunjung setia Catatan Matematika, kali ini Bang RP (Reikson Panjaitan, S.Pd) berbagi Kumpulan Soal Deret Geometri Tak Hingga beserta pembahasannya. Ayo... manfaatkan website Catatan Matematika ini untuk belajar matematika secara online.
128 + 64 + 32 + 16 + ….
Jumlah tak hingga deret geometri tersebut adalah …
A. $85\frac{1}{3}$
B. 110
C. 220
D. 256
E. 512
$r=\frac{U_2}{U_1}=\frac{64}{128}=\frac{1}{2}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{128}{1-\frac{1}{2}}=\frac{128}{\frac{1}{2}}=128\times \frac{2}{1}=256$
Jawaban: D
$2+\frac{2}{3}+\frac{2}{9}+\frac{2}{27}+...$ adalah …
A. $\frac{2}{81}$
B. $\frac{2}{3}$
C. $\frac{80}{27}$
D. 3
E. 6
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{2}{1-\frac{1}{3}}=\frac{2}{\frac{2}{3}}=2\times \frac{3}{2}=3$
Jawaban: D
A. 120
B. 144
C. 240
D. 250
E. 260
Panjang lintasan seluruhnya hingga ayunan berhenti adalah:
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{90}{1-\frac{5}{8}}=\frac{90}{\frac{3}{8}}=90\times \frac{8}{3}=240$
Jadi, panjang lintasan seluruhnya hingga ayunan berhenti adalah 240 cm.
Jawaban: C
A. 17
B. 14
C. 8
D. 6
E. 4
Panjang lintasan bola turun:
$S_{turun}=\frac{h}{1-r}$ maka:
$S_{turun}=\frac{2}{1-\frac{3}{4}}=\frac{2}{\frac{1}{4}}=2\times \frac{4}{1}=8$
Panjang lintasan bola naik:
$S_{naik}=\frac{hr}{1-r}$ maka:
$S_{naik}=\frac{2.\frac{3}{4}}{1-\frac{3}{4}}=\frac{\frac{3}{2}}{\frac{1}{4}}=\frac{3}{2}\times \frac{4}{1}=6$
Panjang seluruh lintasan hingga bola berhenti adalah:
= $S_{turun}+S_{naik}$
= 8 + 6
= 14 meter
Jawaban: B
Cara alternatif (smart solution):
Jika bola dijatuhkan dari ketinggian $h=2$ dan memantul $\frac{p}{q}=\frac{3}{4}$ dari tinggi sebelumnya, maka panjang lintasan bola hingga berhenti adalah:
= $h\times \frac{q+p}{q-p}$
= $2\times \frac{4+3}{4-3}$
= 14 meter
Jawaban: B
A. $32\frac{2}{5}$
B. $21\frac{3}{5}$
C. $18\frac{9}{13}$
D. $12\frac{6}{13}$
E. $10\frac{4}{5}$
$S_{\infty }=81$ dan $a=27$ maka $S_{genap}=...?$
$\begin{align}S_{\infty } &= \frac{a}{1-r} \\ 81 &= \frac{27}{1-r} \\ 81-81r &= 27 \\ -81r &= -54 \\ r &= \frac{-54}{-81} \\ r &= \frac{2}{3} \end{align}$
$\begin{align}S_{genap} &= \frac{ar}{1-r^2} \\ &= \frac{27.\frac{2}{3}}{1-\left( \frac{2}{3} \right)^2} \\ &= \frac{18}{1-\frac{4}{9}} \\ &= \frac{18}{\frac{5}{9}} \\ &= 18\times \frac{9}{5} \\ &= \frac{162}{5} \\ S_{genap} &= 32\frac{2}{5} \end{align}$
Jawaban: A
A. 2
B. 3
C. 4
D. 5
E. 6
$S_{\infty }=6$ dan $S_{genap}=2$ maka $a$ = …?
$\begin{align}S_{\infty } &= 6 \\ \frac{a}{1-r} &= 6 \\ a &= 6(1-r) \end{align}$
$\begin{align}S_{genap} &= 2 \\ \frac{ar}{1-r^2} &= 2 \\ \frac{6(1-r)r}{(1-r)(1+r)} &= 2 \\ \frac{6r}{1+r} &= 2 \\ 6r &= 2+2r \\ 4r &= 2 \\ r &= \frac{1}{2} \end{align}$
Substitusi $r=\frac{1}{2}$ ke persamaan:
$a=6(1-r)=6-6r=6-6.\frac{1}{2}=3$
Jadi, suku pertama deret itu adalah 3.
Jawaban: B
A. 4
B. 6
C. 8
D. 10
E. 12
$S_{\infty }=96$ dan $S_{ganjil}=64$ maka $U_4=...?$
$S_{genap}=S_{\infty }-S_{ganjil}=96-64=32$
$r=\frac{S_{genap}}{S_{ganjil}}=\frac{32}{64}=\frac{1}{2}$
$\begin{align}S_{\infty } &= 96 \\ \frac{a}{1-r} &= 96 \\ a &= 96-96r \\ a &= 96-96\times \frac{1}{2} \\ a &= 96-48 \\ a &= 48 \end{align}$
$U_n=ar^{n-1}$ maka:
$U_4=ar^3=48.\left( \frac{1}{2} \right)^3=48.\frac{1}{8}=6$
Jawaban: B
A. 4
B. 1
C. $\frac{1}{2}$
D. $-4$
E. $-8$
$\begin{align}-\frac{8}{3} &= \frac{a}{1-r} \\ -8+8r &= 3a \\ 8r &= 3a+8 \\ r &= \frac{3a+8}{8} \end{align}$
$\begin{align}\left| r \right| < 1 \\ \left| \frac{3a+8}{8} \right| < 1 \\ \left| 3a+8 \right| < 8 \end{align}$
$-8 <3a+8 <8$
$-8-8 <3a+8-8 <8-8$
$-16 <3a <0$
$-\frac{16}{3} <a <0$
Ingat, $U_n=ar^{n-1}$ maka:
$\begin{align}U_2 &= 2 \\ ar &= 2 \\ r &= \frac{2}{a} \end{align}$
$\begin{align}U_4 &= \frac{1}{2} \\ ar^3 &= \frac{1}{2} \\ a\left( \frac{2}{a} \right)^3 &= \frac{1}{2} \\ \frac{8}{a^2} &= \frac{1}{2} \\ a^2 &= 16 \\ a &= \pm 4 \end{align}$
karena $-\frac{16}{3} <a <0$ maka $a=-4$.
Jawaban: D
A. 65
B. 81
C. 90
D. 135
E. 150
$\begin{align}U_1+U_2 &= 45 \\ a+ar &= 45 \\ a(1+r) &= 45 \\ a &= \frac{45}{1+r} \end{align}$
$\begin{align}U_3+U_4 &= 20 \\ ar^2+ar^3 &= 20 \\ a(r^2+r^3) &= 20 \\ \frac{45}{1+r}.r^2(1+r) &= 20 \\ 45r^2 &= 20 \\ r^2 &= \frac{20}{45} \\ r^2 &= \frac{4}{9} \\ r &= \frac{2}{3} \end{align}$
$a=\frac{45}{1+r}=\frac{45}{1+\frac{2}{3}}=45\times \frac{3}{5}=27$
$S_{\infty }=\frac{a}{1-r}=\frac{27}{1-\frac{2}{3}}=\frac{27}{\frac{1}{3}}=81$
Jawaban: B
A. $\frac{4}{3}$
B. $\frac{3}{2}$
C. 2
D. 3
E. 4
$\begin{align}S_{\infty } &= \frac{a}{1-r} \\ 4a &= \frac{a}{1-\frac{1}{a}} \\ 4a-4 &= a \\ 3a &= 4 \\ a &= \frac{4}{3} \end{align}$
Jawaban: A
A. $1\frac{1}{4} <S <1\frac{1}{2}$
B. $1\frac{1}{5} <S <1\frac{1}{3}$
C. $1\frac{1}{6} <S <1\frac{1}{4}$
D. $1\frac{1}{7} <S <1\frac{1}{5}$
E. $1\frac{1}{8} <S <1\frac{1}{6}$
Syarat deret geometri tak hingga:
$\begin{align}\left| r \right| < 1 \\ \left| \frac{4-3S}{S-1} \right| < 1 \\ \left| 4-3S \right| < \left| S-1 \right| \end{align}$
$\begin{align}(4-3S+S-1)(4-3S-S+1) < 0 \\ (3-2S)(5-4S) < 0 \\ (2S-3)(4S-5) < 0 \end{align}$
Pembuat nol: $S=\frac{3}{2}$ atau $S=\frac{5}{4}$
Jadi, $\frac{5}{4} <S <\frac{3}{2}\Leftrightarrow 1\frac{1}{4} <S <1\frac{1}{2}$.
Jawaban: A
A. $\frac{6}{7} <x <2$
B. $\frac{5}{7} <x <3$
C. $\frac{4}{7} <x <4$
D. $\frac{3}{7} <x <5$
E. $\frac{2}{7} <x <6$
Syarat deret geometri konvergen adalah:
$-1 <r <1$
$-1 < {^7\log (2x-1)} < 1 $
$^7\log 7^{-1} < {^7\log (2x-1)} < {^7\log 7}$
$^7\log \frac{1}{7} < {^7\log (2x-1)} < {^7\log 7}$
$\frac{1}{7} <2x-1 <7$
$\frac{1}{7}+1 <2x-1+1 <7+1$
$\frac{8}{7} <2x <8$
$\frac{4}{7} <x <4$
Jawaban: C
A. $x <\frac{1}{2}$
B. $0 <x <1$
C. $-\frac{1}{2} <x <\frac{1}{2}$
D. $0 <x <\frac{1}{2}$
E. $-\frac{1}{2} <x <0$
$S_{\infty }=1$ dan $a=2x+1$
$\begin{align}S_{\infty } &= \frac{a}{1-r} \\ 1 &= \frac{2x+1}{1-r} \\ 1-r &= 2x+1 \\ -r &= 2x \\ r &= -2x \end{align}$
Ingat:
$-1 < r < 1$
$-1 < -2x < 1$
$1 > 2x > -1$
$\frac{1}{2} > x > -\frac{1}{2}$
Jadi, $-\frac{1}{2} < x < \frac{1}{2}$
Jawaban: C
A. 5,5 meter
B. 7,5 meter
C. 9 meter
D. 10 meter
E. 12,5 meter
Panjang lintasan bola turun:
$S_{turun}=\frac{h}{1-r}$ maka:
$S_{turun}=\frac{\frac{5}{2}}{1-\frac{3}{5}}=\frac{\frac{5}{2}}{\frac{2}{5}}=\frac{5}{2}\times \frac{5}{2}=\frac{25}{4}$
Panjang lintasan bola naik:
$S_{naik}=\frac{hr}{1-r}$ maka:
$S_{naik}=\frac{\frac{5}{2}.\frac{3}{5}}{1-\frac{3}{5}}=\frac{\frac{3}{2}}{\frac{2}{5}}=\frac{3}{2}\times \frac{5}{2}=\frac{15}{4}$
Panjang seluruh lintasan hingga bola berhenti adalah:
= $S_{turun}+S_{naik}$
= $\frac{25}{4}+\frac{15}{4}$
= 10 meter
Jawaban: D
Cara alternatif (smart solution):
Jika bola dijatuhkan dari ketinggian $h=2,5=\frac{5}{2}$ dan memantul $\frac{p}{q}=\frac{3}{5}$ dari tinggi sebelumnya, maka panjang lintasan bola hingga berhenti adalah:
= $h\times \frac{q+p}{q-p}$
= $\frac{5}{2}\times \frac{5+3}{5-3}$
= 10 meter
Jawaban: D
A. $\sin x$
B. $\frac{1+\cos x}{\sin x}$
C. $\tan \frac{1}{2}x$
D. $\frac{\sin x}{1+\cos x}$
E. $\cos x$
$r=\frac{U_2}{U_1}=\frac{\cos x\sin x}{\sin x}=\cos x$
$S_{\infty }=\frac{a}{1-r}$ maka:
$\begin{align}S_{\infty } &= \frac{\sin x}{1-\cos x} \\ &= \frac{\sin x}{1-\cos x}\times \frac{1+\cos x}{1+\cos x} \\ &= \frac{\sin x(1+\cos x)}{1-{{\cos }^{2}}x} \\ &= \frac{\sin x(1+\cos x)}{{{\sin }^{2}}x} \\ S_{\infty } &= \frac{1+\cos x}{\sin x} \end{align}$
Jawaban: B

A. $\frac{4}{3}a^2\sqrt{3}$
B. $\frac{3}{4}a^2\sqrt{3}$
C. $\frac{1}{4}a^2\sqrt{3}$
D. $\frac{1}{3}a^2\sqrt{3}$
E. $\frac{2}{3}a^2\sqrt{3}$
Luas ABC = $\frac{1}{4}a^2\sqrt{3}$
Luas A'B'C' = $\frac{1}{4}$Luas ABC = $\frac{1}{16}a^2\sqrt{3}$
Luas A"B"C" = $\frac{1}{4}$Luas A’B’C’ = $\frac{1}{64}a^2\sqrt{3}$
Jadi, luas ABC + luas A'B'C' + luas A"B"C" + … adalah:
= $\frac{1}{4}s\sqrt{3}$ + $\frac{1}{16}a^2\sqrt{3}$ + $\frac{1}{64}a^2\sqrt{3}$ + …
Jumlah luas segitiga membentuk deret geometri tak hingga dengan $U_1=\frac{1}{4}a^2\sqrt{3}$ dan $r=\frac{1}{4}$ yang jumlahnya adalah:
= $\frac{U_1}{1-r}$
= $\frac{\frac{1}{4}a^2\sqrt{3}}{1-\frac{1}{4}}$
= $\frac{\frac{1}{4}a^2\sqrt{3}}{\frac{3}{4}}$
= $\frac{1}{4}a^2\sqrt{3}\times \frac{4}{3}$
= $\frac{1}{3}a^2\sqrt{3}$
Jawaban: D

A. $2a^2$
B. $3a^2$
C. $4a^2$
D. $5a^2$
E. $\infty $
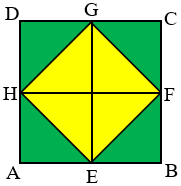
Luas ABCD = $a^2$
Luas EFGH = $\frac{1}{2}$ x luas EFGH
Luas EFGH = $\frac{1}{2}a^2$
Perhatikan gambar berikut!

Luas IJKL = $\frac{1}{2}$Luas segitiga EFGH
Luas IJKL = $\frac{1}{2}\times \frac{1}{2}a^2$ = $\frac{1}{4}a^2$
Jumlah luas persegi yang terbentuk jika diteruskan akan membentuk deret geometri tak hingga yaitu: $a+\frac{1}{2}a^2+\frac{1}{4}a^2+...$ dengan $U_1=a^2$ dan $r=\frac{1}{2}$.
Jumlah seluruhnya:
= $\frac{U_1}{1-r}$ = $\frac{a^2}{1-\frac{1}{2}}$ = $\frac{a^2}{\frac{1}{2}}$ = $2a^2$
Jawaban: A
A. $-96$
B. $-64$
C. $-36$
D. $-24$
E. $-12$
$(x-50)$, $(x-14)$, $(x-5)$
Syarat barisan geometri:
$\begin{align}\frac{U_2}{U_1} &= \frac{U_3}{U_2} \\ \frac{x-14}{x-50} &= \frac{x-5}{x-14} \\ (x-14)(x-14) &= (x-50)(x-5) \\ x^2-28x+196 &= x^2-55x+250 \\ -28x+196 &= -55x+250 \\ -28x+55x &= 250-196 \\ 27x &= 54 \\ x &= \frac{54}{27} \\ x &= 2 \end{align}$
$\begin{align}a &= x-50 \\ &= 2-50 \\ a &= -48 \end{align}$
$\begin{align}U_2 &= x-14 \\ &= 2-14 \\ U_2 &= -12 \end{align}$
$r=\frac{U_2}{U_1}=\frac{x-14}{x-50}=\frac{2-14}{2-50}=\frac{-12}{-48}r=\frac{1}{4}$
jumlah semua suku-sukunya adalah:
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{-48}{1-\frac{1}{4}}=\frac{-48}{\frac{3}{4}}=-48\times \frac{4}{3}=-64$
Jawaban: B
A. $-1 <x <1$
B. $0 <x <2$
C. $2 <x <\infty $
D. $-\infty <x <2$
E. $-\infty <x <\infty $
$\begin{align}\left| r \right| & <1 \\ \left| \frac{U_2}{U_1} \right| & < 1 \end{align}$
$\left| \frac{(x-1)^2}{x-1} \right| < 1$
$\left| x-1 \right| < 1$
$-1 < x-1 < 1$
$-1+1 < x-1+1 < 1+1$
$0 < x < 2$
Jawaban: B
A. $3\frac{1}{2} < x < 5$
B. $3\frac{1}{2}\le x\le 5$
C. $0\le \left| x-3 \right|\le 2$
D. $0 < \left| x-3 \right|\le 2$
E. $0 < \left| x-3 \right| < 2$
$-1 < r < 1$
$-1 < \frac{U_2}{U_1} < 1$
$-1 < \frac{^{2}\log (x-3)}{1} < 1$
$-1{{ < }^{2}}\log (x-3) < 1$
$^{2}\log {{2}^{-1}}{{ < }^{2}}\log (x-3){{ < }^{2}}\log 2$
${{2}^{-1}} < x-3 < 2$
$\frac{1}{2} < x-3 < 2$
$\frac{1}{2}+3 < x-3+3 < 2+3$
$3\frac{1}{2} < x < 5$
Jawaban: A
A. $\frac{4}{3}$
B. $\frac{5}{3}$
C. $\frac{12}{3}$
D. $\frac{15}{3}$
E. $\frac{16}{3}$
$a=4$ dan $r=\frac{U_2}{U_1}=\frac{1}{4}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{4}{1-\frac{1}{4}}=\frac{4}{\frac{3}{4}}=4\times \frac{4}{3}=\frac{16}{3}$
Jawaban: E
A. $74\frac{1}{7}$
B. $74\frac{1}{8}$
C. 74
D. $73\frac{1}{7}$
E. $73\frac{1}{8}$
$a=64$ dan $r=\frac{U_2}{U_1}=\frac{8}{64}=\frac{1}{8}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{64}{1-\frac{1}{8}}=\frac{4}{\frac{7}{8}}=64\times \frac{8}{7}=\frac{512}{7}=73\frac{1}{7}$
Jawaban: D
A. $26\frac{2}{3}$
B. 27
C. 36
D. $38\frac{7}{6}$
E. 54
$a=18$ dan $r=\frac{U_2}{U_1}=\frac{6}{18}=\frac{1}{3}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{18}{1-\frac{1}{3}}=\frac{18}{\frac{2}{3}}=18\times \frac{3}{2}=27$
Jawaban: B
A. $\infty $
B. 9
C. $8\frac{1}{2}$
D. 8
E. $7\frac{3}{4}$
$a=4$ dan $r=\frac{U_2}{U_1}=\frac{2}{4}=\frac{1}{2}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{4}{1-\frac{1}{2}}=\frac{4}{\frac{1}{2}}=4\times \frac{2}{1}=8$
Jawaban: D
A. 10
B. 11
C. 12
D. 13
E. 14
$a=6$ dan $r=\frac{U_2}{U_1}=\frac{3}{6}=\frac{1}{2}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{6}{1-\frac{1}{2}}=\frac{6}{\frac{1}{2}}=6\times \frac{2}{1}=12$
Jawaban: C
A. $\frac{2}{3}\left( \sqrt{2}+1 \right)$
B. $\frac{3}{2}\left( \sqrt{2}+1 \right)$
C. $2\left( \sqrt{2}+1 \right)$
D. $3\left( \sqrt{2}+1 \right)$
E. $4\left( \sqrt{2}+1 \right)$
$a=\sqrt{2}$ dan $r=\frac{U_2}{U_1}=\frac{1}{\sqrt{2}}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$\begin{align}S_{\infty } &= \frac{\sqrt{2}}{1-\frac{1}{\sqrt{2}}} \\ &= \frac{\sqrt{2}}{\frac{\sqrt{2}-1}{\sqrt{2}}} \\ &= \sqrt{2}\times \frac{\sqrt{2}}{\sqrt{2}-1} \\ &= \frac{2}{\sqrt{2}-1}\times \frac{\sqrt{2}+1}{\sqrt{2}+1} \\ S_{\infty } &= 2(\sqrt{2}+1) \end{align}$
Jawaban: C
A. $2+\sqrt{2}$
B. $2-\sqrt{2}$
C. $-2-\sqrt{2}$
D. $-2+\sqrt{2}$
E. $2+\sqrt{3}$
Ingat, $S_{ganjil}=\frac{a}{1-r^2}$ maka:
$\begin{align}S_{ganjil} &= 2 \\ \frac{a}{1-r^2} &= 2 \\ \frac{1}{1-r^2} &= 2 \\ 1 &= 2-2r^2 \\ 2r^2 &= 1 \\ r^2 &= \frac{1}{2} \\ r &= \frac{1}{\sqrt{2}} \end{align}$
$\begin{align}S_{\infty } &= \frac{a}{1-r} \\ &= \frac{1}{1-\frac{1}{\sqrt{2}}} \\ &= \frac{1}{\frac{\sqrt{2}-1}{\sqrt{2}}} \\ &= \frac{\sqrt{2}}{\sqrt{2}-1}\times \frac{\sqrt{2}+1}{\sqrt{2}+1} \\ &= \frac{2+\sqrt{2}}{2-1} \\ S_{\infty } &= 2+\sqrt{2} \end{align}$
Jawaban: A
A. 3,38 meter
B. 3,75 meter
C. 4,25 meter
D. 6,75 meter
E. 7,75 meter
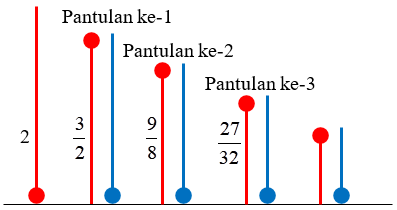
Panjang lintasan bola tersebut dari pantulan ke-3 sampai ia berhenti adalah dua kali jumlah deret geometri tak hingga dengan $a=\frac{27}{32}$ dan $r=\frac{3}{4}$.
$\begin{align}2\times S_{\infty } &= 2.\frac{a}{1-r} \\ &= 2.\frac{\frac{27}{32}}{1-\frac{3}{4}} \\ &= \frac{2.\frac{27}{32}}{\frac{1}{4}} \\ &= \frac{27}{16}\times \frac{4}{1} \\ &= \frac{27}{4} \\ &= 6,75 \end{align}$
Jadi, panjang lintasan bola tersebut dari pantulan ke-3 sampai ia berhenti adalah 6,75 meter.
Jawaban: D
A. 60 m
B. 70 m
C. 80 m
D. 90 m
E. 100 m
Panjang lintasan bola turun:
$S_{turun}=\frac{h}{1-r}$ maka:
$S_{turun}=\frac{10}{1-\frac{3}{4}}=\frac{10}{\frac{1}{4}}=10\times \frac{4}{1}=40$
Panjang lintasan bola naik:
$S_{naik}=\frac{hr}{1-r}$ maka:
$S_{naik}=\frac{10.\frac{3}{4}}{1-\frac{3}{4}}=\frac{\frac{15}{2}}{\frac{1}{4}}=\frac{15}{2}\times \frac{4}{1}=30$
Panjang seluruh lintasan hingga bola berhenti adalah:
= $S_{turun}+S_{naik}$
= 40 + 30
= 70 meter
Jawaban: B
Cara alternatif (smart solution):
Jika bola dijatuhkan dari ketinggian $h=10$ meter dan memantul $\frac{p}{q}=\frac{3}{4}$ dari tinggi sebelumnya, maka panjang lintasan bola hingga berhenti adalah:
= $h\times \frac{q+p}{q-p}$
= $10\times \frac{4+3}{4-3}$
= 70 meter
Jawaban: B
A. 16 m
B. 18 m
C. 20 m
D. 24 m
E. 30 m
Rasio pantulan bola adalah:
$r=\frac{\frac{8}{3}}{4}=\frac{8}{3}\times \frac{1}{4}=\frac{2}{3}$
Panjang lintasan bola turun:
$S_{turun}=\frac{h}{1-r}$ maka:
$S_{turun}=\frac{6}{1-\frac{2}{3}}=\frac{6}{\frac{1}{3}}=6\times \frac{3}{1}=18$
Panjang lintasan bola naik:
$S_{naik}=\frac{hr}{1-r}$ maka:
$S_{naik}=\frac{6.\frac{2}{3}}{1-\frac{2}{3}}=\frac{4}{\frac{1}{3}}=4\times \frac{3}{1}=12$
Panjang seluruh lintasan hingga bola berhenti adalah:
= $S_{turun}+S_{naik}$
= 18 + 12
= 30 meter
Jawaban: E
Cara alternatif (smart solution):
Jika bola dijatuhkan dari ketinggian $h=6$ meter dan memantul $\frac{p}{q}=\frac{2}{3}$ dari tinggi sebelumnya, maka panjang lintasan bola hingga berhenti adalah:
= $h\times \frac{q+p}{q-p}$
= $6\times \frac{3+2}{3-2}$
= 30 meter
Jawaban: E
A. 2 m
B. 3 m
C. 5 m
D. 7 m
E. 8 m
Panjang lintasan bola turun:
$S_{turun}=\frac{h}{1-r}$ maka:
$S_{turun}=\frac{1}{1-\frac{3}{4}}=\frac{1}{\frac{1}{4}}=4$
Panjang lintasan bola naik:
$S_{naik}=\frac{hr}{1-r}$ maka:
$S_{naik}=\frac{1.\frac{3}{4}}{1-\frac{3}{4}}=\frac{\frac{3}{4}}{\frac{1}{4}}=\frac{3}{4}\times \frac{4}{1}=3$
Panjang seluruh lintasan hingga bola berhenti adalah:
= $S_{turun}+S_{naik}$
= 4 + 3
= 7 meter
Jawaban: D
Cara alternatif (smart solution):
Jika bola dijatuhkan dari ketinggian $h=1$ meter dan memantul $\frac{p}{q}=\frac{3}{4}$ dari tinggi sebelumnya, maka panjang lintasan bola hingga berhenti adalah:
= $h\times \frac{q+p}{q-p}$
= $1\times \frac{4+3}{4-3}$
= 7 meter
Jawaban: D
A. $\frac{1}{3}$
B. $\frac{2}{3}$
C. 1
D. $\frac{5}{6}$
E. $\frac{4}{3}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{1}{1+\frac{1}{2}}=\frac{1}{\frac{3}{2}}=\frac{2}{3}$
Jawaban: B
A. $x > 0$
B. $x < 1$
C. $x > 2$
D. $0 < x < 1$
E. $x < 0$ atau $x > 2$
Syarat deret geometri konvergen:
$\begin{align}\left| r \right| & < 1 \\ \left| \frac{1}{x-1} \right| & < 1 \\ \left| x-1 \right| & > 1 \end{align}$
$x-1 < -1$ atau $x-1 >1$ maka:
$x < 0$ atau $x >2$
Jawaban: E
A. $\frac{1}{4} < S < \frac{1}{2}$
B. $\frac{3}{8} < S < \frac{3}{4}$
C. $\frac{1}{3} < S < 1$
D. $\frac{3}{4} < S < \frac{4}{3}$
E. $\frac{1}{5} < S < \frac{4}{5}$
$S=\frac{a}{1-r}$ maka:
$\begin{align}S &= \frac{\frac{1}{3+r}}{1-\frac{1}{3+r}} \\ &= \frac{\frac{1}{3+r}}{\frac{3+r-1}{3+r}} \\ &= \frac{1}{3+r}\times \frac{3+r}{2+r} \\ S &= \frac{1}{r+2} \\ r+2 &= \frac{1}{S} \\ r &= \frac{1}{S}-2 \\ r &= \frac{1-2S}{S} \end{align}$
Syarat deret geometri tak hingga:
$\begin{align}\left| r \right| & < 1 \\ \left| \frac{1-2S}{S} \right| & < 1 \\ \frac{\left| 1-2S \right|}{\left| S \right|} & < 1 \\ \left| 1-2S \right| & < \left| S \right| \\ (1-2S+S)(1-2S-S) & < 0 \\ (1-S)(1-3S) & < 0 \end{align}$
$1-S=0\to S=1$
$1-3S=0\to S=\frac{1}{3}$
Jadi, $\frac{1}{3} < S < 1$.
Jawaban: C
A. $\frac{\cos x+\sin x}{\sin x}$
B. $\frac{1+\cos x}{\sin x}$
C. $\frac{\sin x}{1+\cos x}$
D. $\frac{1+\sin x}{\cos x}$
E. $\frac{\cos x}{1+\sin x}$
$a=\cos x$ dan $r=\frac{U_2}{U_1}=\frac{\cos x\sin x}{\cos x}=\sin x$
$S_{\infty }=\frac{a}{1-r}$ maka:
$\begin{align}S_{\infty } &= \frac{\cos x}{1-\sin x} \\ &= \frac{\cos x}{1-\sin x}\times \frac{1+\sin x}{1+\sin x} \\ &= \frac{\cos x(1+\sin x)}{1-{{\sin }^{2}}x} \\ &= \frac{\cos x(1+\sin x)}{{{\cos }^{2}}x} \\ S_{\infty } &= \frac{1+\sin x}{\cos x} \end{align}$
Jawaban: D
A. 3, $\frac{3}{4}$, $\frac{3}{16}$, …
B. 3, $\frac{3}{8}$, $\frac{3}{64}$, …
C. 3, $\frac{3}{2}$, $\frac{3}{4}$, …
D. $\frac{3}{8}$, $\frac{3}{4}$, $\frac{3}{2}$, 3, …
E. $\frac{3}{8}$, $\frac{3}{6}$, $\frac{3}{2}$, …
$S_{ganjil}=4$ dan $S_{\infty }=6$
$S_{genap}=S_{\infty }-S_{ganjil}=6-4=2$
$r=\frac{S_{genap}}{S_{ganjil}}=\frac{2}{4}=\frac{1}{2}$
$\begin{align}S_{\infty } &= 6 \\ \frac{a}{1-r} &= 6 \\ a &= 6-6r \\ a &= 6-6.\frac{1}{2} \\ a &= 3 \end{align}$
Deret geometri tersebut adalah:
$a$, $ar$, $ar^2$, …
3, $\frac{3}{2}$, $\frac{3}{4}$, ….
Jawaban: C
A. 2
B. 1
C. $\frac{1}{2}$
D. $\frac{1}{3}$
E. $\frac{1}{4}$
$S_{\infty }=8$ dan $S_{genap}=\frac{8}{3}$ maka $U_5$ = …
$\begin{align}S_{\infty } &= 8 \\ \frac{a}{1-r} &= 8 \\ a &= 8-8r \end{align}$
Ingat, $S_{genap}=\frac{ar}{1-r^2}$ maka:
$\begin{align}S_{genap} &= \frac{8}{3} \\ \frac{ar}{1-r^2} &= \frac{8}{3} \\ 3ar &= 8-8r^2 \\ 3(8-8r)r &= 8-8r^2 \\ 24r-24r^2 &= 8-8r^2 \\ -16r^2+24r-8 &= 0 \\ 2r^2-3r+1 &= 0 \\ (2r-1)(r-1) &= 0 \end{align}$
$2r-1=0\to r=\frac{1}{2}$
$r-1=0\to r=1$
Karena $-1 < r < 1$ maka $r=\frac{1}{2}$.
$\begin{align}S_{\infty } &= 8 \\ \frac{a}{1-r} &= 8 \\ \frac{a}{1-\frac{1}{2}} &= 8 \\ a &= 4 \end{align}$
Ingat, $U_n=ar^{n-1}$ maka:
$U_5=a{{r}^{4}}=4.{{\left( \frac{1}{2} \right)}^{4}}=\frac{1}{4}$
Jawaban: E
Tata Cara Belajar:
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cek jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cek jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
Soal No. 1
Diketahui deret geometri:128 + 64 + 32 + 16 + ….
Jumlah tak hingga deret geometri tersebut adalah …
A. $85\frac{1}{3}$
B. 110
C. 220
D. 256
E. 512
Penyelesaian: Lihat/Tutup
$a=128$$r=\frac{U_2}{U_1}=\frac{64}{128}=\frac{1}{2}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{128}{1-\frac{1}{2}}=\frac{128}{\frac{1}{2}}=128\times \frac{2}{1}=256$
Jawaban: D
Soal No. 2
Jumlah tak hingga deret geometri:$2+\frac{2}{3}+\frac{2}{9}+\frac{2}{27}+...$ adalah …
A. $\frac{2}{81}$
B. $\frac{2}{3}$
C. $\frac{80}{27}$
D. 3
E. 6
Penyelesaian: Lihat/Tutup
$a=2$ dan $r=\frac{U_2}{U_1}=\frac{\frac{2}{3}}{2}=\frac{1}{3}$$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{2}{1-\frac{1}{3}}=\frac{2}{\frac{2}{3}}=2\times \frac{3}{2}=3$
Jawaban: D
Soal No. 3
Sebuah ayunan mencapai lintasan pertama sejauh 90 cm, dan lintasan berikutnya hanya mencapai $\frac{5}{8}$ dari lintasan sebelumnya. Panjang lintasan seluruhnya hingga ayunan berhenti adalah … cm.A. 120
B. 144
C. 240
D. 250
E. 260
Penyelesaian: Lihat/Tutup
$a=90$ dan $r=\frac{5}{8}$Panjang lintasan seluruhnya hingga ayunan berhenti adalah:
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{90}{1-\frac{5}{8}}=\frac{90}{\frac{3}{8}}=90\times \frac{8}{3}=240$
Jadi, panjang lintasan seluruhnya hingga ayunan berhenti adalah 240 cm.
Jawaban: C
Soal No. 4
Sebuah bola pingpong dijatuhkan ke lantai dari ketinggian 2 meter. Setiap bola itu memantul ia mencapai ketinggian $\frac{3}{4}$ dari ketinggian yang dicapai sebelumnya. Panjang lintasan bola tersebut hingga bola berhenti adalah … meter.A. 17
B. 14
C. 8
D. 6
E. 4
Penyelesaian: Lihat/Tutup
Bola dijatuhkan dari ketinggian (h) 2 meter dan memantul dengan r = $\frac{3}{4}$Panjang lintasan bola turun:
$S_{turun}=\frac{h}{1-r}$ maka:
$S_{turun}=\frac{2}{1-\frac{3}{4}}=\frac{2}{\frac{1}{4}}=2\times \frac{4}{1}=8$
Panjang lintasan bola naik:
$S_{naik}=\frac{hr}{1-r}$ maka:
$S_{naik}=\frac{2.\frac{3}{4}}{1-\frac{3}{4}}=\frac{\frac{3}{2}}{\frac{1}{4}}=\frac{3}{2}\times \frac{4}{1}=6$
Panjang seluruh lintasan hingga bola berhenti adalah:
= $S_{turun}+S_{naik}$
= 8 + 6
= 14 meter
Jawaban: B
Cara alternatif (smart solution):
Jika bola dijatuhkan dari ketinggian $h=2$ dan memantul $\frac{p}{q}=\frac{3}{4}$ dari tinggi sebelumnya, maka panjang lintasan bola hingga berhenti adalah:
= $h\times \frac{q+p}{q-p}$
= $2\times \frac{4+3}{4-3}$
= 14 meter
Jawaban: B
Soal No. 5
Jumlah tak hingga deret geometri adalah 81 dan suku pertamanya adalah 27. Jumlah semua suku bernomor genap deret tersebut adalah ….A. $32\frac{2}{5}$
B. $21\frac{3}{5}$
C. $18\frac{9}{13}$
D. $12\frac{6}{13}$
E. $10\frac{4}{5}$
Penyelesaian: Lihat/Tutup
Deret geometri tak hingga:$S_{\infty }=81$ dan $a=27$ maka $S_{genap}=...?$
$\begin{align}S_{\infty } &= \frac{a}{1-r} \\ 81 &= \frac{27}{1-r} \\ 81-81r &= 27 \\ -81r &= -54 \\ r &= \frac{-54}{-81} \\ r &= \frac{2}{3} \end{align}$
$\begin{align}S_{genap} &= \frac{ar}{1-r^2} \\ &= \frac{27.\frac{2}{3}}{1-\left( \frac{2}{3} \right)^2} \\ &= \frac{18}{1-\frac{4}{9}} \\ &= \frac{18}{\frac{5}{9}} \\ &= 18\times \frac{9}{5} \\ &= \frac{162}{5} \\ S_{genap} &= 32\frac{2}{5} \end{align}$
Jawaban: A
Soal No. 6
Jumlah semua suku suatu deret geometri tak berhingga adalah 6 dan jumlah suku-suku yang bernomor genap adalah 2, maka suku pertama deret itu adalah ….A. 2
B. 3
C. 4
D. 5
E. 6
Penyelesaian: Lihat/Tutup
Deret geometri tak berhingga:$S_{\infty }=6$ dan $S_{genap}=2$ maka $a$ = …?
$\begin{align}S_{\infty } &= 6 \\ \frac{a}{1-r} &= 6 \\ a &= 6(1-r) \end{align}$
$\begin{align}S_{genap} &= 2 \\ \frac{ar}{1-r^2} &= 2 \\ \frac{6(1-r)r}{(1-r)(1+r)} &= 2 \\ \frac{6r}{1+r} &= 2 \\ 6r &= 2+2r \\ 4r &= 2 \\ r &= \frac{1}{2} \end{align}$
Substitusi $r=\frac{1}{2}$ ke persamaan:
$a=6(1-r)=6-6r=6-6.\frac{1}{2}=3$
Jadi, suku pertama deret itu adalah 3.
Jawaban: B
Soal No. 7
Jika jumlah semua suku deret geometri tak hingga adalah 96 dan jumlah semua suku yang berindeks ganjil adalah 64, maka suku ke-4 deret tersebut adalah …A. 4
B. 6
C. 8
D. 10
E. 12
Penyelesaian: Lihat/Tutup
Deret geometri tak hingga:$S_{\infty }=96$ dan $S_{ganjil}=64$ maka $U_4=...?$
$S_{genap}=S_{\infty }-S_{ganjil}=96-64=32$
$r=\frac{S_{genap}}{S_{ganjil}}=\frac{32}{64}=\frac{1}{2}$
$\begin{align}S_{\infty } &= 96 \\ \frac{a}{1-r} &= 96 \\ a &= 96-96r \\ a &= 96-96\times \frac{1}{2} \\ a &= 96-48 \\ a &= 48 \end{align}$
$U_n=ar^{n-1}$ maka:
$U_4=ar^3=48.\left( \frac{1}{2} \right)^3=48.\frac{1}{8}=6$
Jawaban: B
Soal No. 8
Jika deret geometri konvergen dengan limit $-\frac{8}{3}$ dan suku ke-2 serta ke-4 berturut-turut 2 dan $\frac{1}{2}$ maka suku pertamanya adalah ….A. 4
B. 1
C. $\frac{1}{2}$
D. $-4$
E. $-8$
Penyelesaian: Lihat/Tutup
$S_{\infty }=-\frac{8}{3}$, $U_2=2$, $U_4=\frac{1}{2}$ maka $a=...?$$\begin{align}-\frac{8}{3} &= \frac{a}{1-r} \\ -8+8r &= 3a \\ 8r &= 3a+8 \\ r &= \frac{3a+8}{8} \end{align}$
$\begin{align}\left| r \right| < 1 \\ \left| \frac{3a+8}{8} \right| < 1 \\ \left| 3a+8 \right| < 8 \end{align}$
$-8 <3a+8 <8$
$-8-8 <3a+8-8 <8-8$
$-16 <3a <0$
$-\frac{16}{3} <a <0$
Ingat, $U_n=ar^{n-1}$ maka:
$\begin{align}U_2 &= 2 \\ ar &= 2 \\ r &= \frac{2}{a} \end{align}$
$\begin{align}U_4 &= \frac{1}{2} \\ ar^3 &= \frac{1}{2} \\ a\left( \frac{2}{a} \right)^3 &= \frac{1}{2} \\ \frac{8}{a^2} &= \frac{1}{2} \\ a^2 &= 16 \\ a &= \pm 4 \end{align}$
karena $-\frac{16}{3} <a <0$ maka $a=-4$.
Jawaban: D
Soal No. 9
Suku-suku suatu barisan geometri tak hingga adalah positif, jumlah suku $U_1+U_2=45$ dan $U_3+U_4=20$, maka jumlah suku-suku barisan itu adalah ….A. 65
B. 81
C. 90
D. 135
E. 150
Penyelesaian: Lihat/Tutup
Suku-suku suatu barisan geometri tak hingga adalah positif, maka $r >0$.$\begin{align}U_1+U_2 &= 45 \\ a+ar &= 45 \\ a(1+r) &= 45 \\ a &= \frac{45}{1+r} \end{align}$
$\begin{align}U_3+U_4 &= 20 \\ ar^2+ar^3 &= 20 \\ a(r^2+r^3) &= 20 \\ \frac{45}{1+r}.r^2(1+r) &= 20 \\ 45r^2 &= 20 \\ r^2 &= \frac{20}{45} \\ r^2 &= \frac{4}{9} \\ r &= \frac{2}{3} \end{align}$
$a=\frac{45}{1+r}=\frac{45}{1+\frac{2}{3}}=45\times \frac{3}{5}=27$
$S_{\infty }=\frac{a}{1-r}=\frac{27}{1-\frac{2}{3}}=\frac{27}{\frac{1}{3}}=81$
Jawaban: B
Soal No. 10
Jika jumlah tak hingga deret $a+1+\frac{1}{a}+\frac{1}{a^2}+...$ adalah $4a$, maka $a$ = ….A. $\frac{4}{3}$
B. $\frac{3}{2}$
C. 2
D. 3
E. 4
Penyelesaian: Lihat/Tutup
$S_{\infty }=4a$$r=\frac{U_2}{U_1}\Leftrightarrow r=\frac{1}{a}$$\begin{align}S_{\infty } &= \frac{a}{1-r} \\ 4a &= \frac{a}{1-\frac{1}{a}} \\ 4a-4 &= a \\ 3a &= 4 \\ a &= \frac{4}{3} \end{align}$
Jawaban: A
Soal No. 11
Jika r rasio dari deret geometri tak hingga yang jumlah-nya mempunyai limit dan S limit jumlah tak hingga $1+\frac{1}{4+r}+\frac{1}{{{(4+r)}^{2}}}+...+\frac{1}{{{(4+r)}^{n}}}+...$ maka …A. $1\frac{1}{4} <S <1\frac{1}{2}$
B. $1\frac{1}{5} <S <1\frac{1}{3}$
C. $1\frac{1}{6} <S <1\frac{1}{4}$
D. $1\frac{1}{7} <S <1\frac{1}{5}$
E. $1\frac{1}{8} <S <1\frac{1}{6}$
Penyelesaian: Lihat/Tutup
$\begin{align}S &= \frac{1}{1-\frac{1}{4+r}} \\ &= \frac{1}{\frac{4+r-1}{4+r}} \\ &= \frac{1}{\frac{3+r}{4+r}} \\ S &= \frac{r+4}{r+3} \\ rS+3S &= r+4 \\ r(S-1) &= 4-3S \\ r &= \frac{4-3S}{S-1} \end{align}$Syarat deret geometri tak hingga:
$\begin{align}\left| r \right| < 1 \\ \left| \frac{4-3S}{S-1} \right| < 1 \\ \left| 4-3S \right| < \left| S-1 \right| \end{align}$
$\begin{align}(4-3S+S-1)(4-3S-S+1) < 0 \\ (3-2S)(5-4S) < 0 \\ (2S-3)(4S-5) < 0 \end{align}$
Pembuat nol: $S=\frac{3}{2}$ atau $S=\frac{5}{4}$
Jadi, $\frac{5}{4} <S <\frac{3}{2}\Leftrightarrow 1\frac{1}{4} <S <1\frac{1}{2}$.
Jawaban: A
Soal No. 12
Ditentukan rasio deret geometri tak hingga adalah $^{7}\log (2x-1)$. Jika deret ini mempunyai jumlah (konvergen) maka nilai $x$ yang memenuhi adalah ...A. $\frac{6}{7} <x <2$
B. $\frac{5}{7} <x <3$
C. $\frac{4}{7} <x <4$
D. $\frac{3}{7} <x <5$
E. $\frac{2}{7} <x <6$
Penyelesaian: Lihat/Tutup
$r$ = $^7\log (2x-1)$Syarat deret geometri konvergen adalah:
$-1 <r <1$
$-1 < {^7\log (2x-1)} < 1 $
$^7\log 7^{-1} < {^7\log (2x-1)} < {^7\log 7}$
$^7\log \frac{1}{7} < {^7\log (2x-1)} < {^7\log 7}$
$\frac{1}{7} <2x-1 <7$
$\frac{1}{7}+1 <2x-1+1 <7+1$
$\frac{8}{7} <2x <8$
$\frac{4}{7} <x <4$
Jawaban: C
Soal No. 13
Jumlah deret geometri tak hingga adalah 1. Jika suku pertama deretnya adalah $2x+1$, maka semua nilai $x$ harus memenuhi pertaksamaan …A. $x <\frac{1}{2}$
B. $0 <x <1$
C. $-\frac{1}{2} <x <\frac{1}{2}$
D. $0 <x <\frac{1}{2}$
E. $-\frac{1}{2} <x <0$
Penyelesaian: Lihat/Tutup
Deret geometri tak hingga:$S_{\infty }=1$ dan $a=2x+1$
$\begin{align}S_{\infty } &= \frac{a}{1-r} \\ 1 &= \frac{2x+1}{1-r} \\ 1-r &= 2x+1 \\ -r &= 2x \\ r &= -2x \end{align}$
Ingat:
$-1 < r < 1$
$-1 < -2x < 1$
$1 > 2x > -1$
$\frac{1}{2} > x > -\frac{1}{2}$
Jadi, $-\frac{1}{2} < x < \frac{1}{2}$
Jawaban: C
Soal No. 14
Sebuah bola jatuh dari ketinggian 2,5 m dan memantul dengan ketinggian $\frac{3}{5}$ kali tinggi semula. Dan setiap kali memantul berikutnya mencapai $\frac{3}{5}$ kali tinggi pantulan sebelumnya. Maka jarak lintasan bola seluruhnya sampai berhenti adalah …A. 5,5 meter
B. 7,5 meter
C. 9 meter
D. 10 meter
E. 12,5 meter
Penyelesaian: Lihat/Tutup
Bola dijatuhkan dari ketinggian h = 2,5 = $\frac{5}{2}$ meter dan memantul dengan r = $\frac{3}{4}$Panjang lintasan bola turun:
$S_{turun}=\frac{h}{1-r}$ maka:
$S_{turun}=\frac{\frac{5}{2}}{1-\frac{3}{5}}=\frac{\frac{5}{2}}{\frac{2}{5}}=\frac{5}{2}\times \frac{5}{2}=\frac{25}{4}$
Panjang lintasan bola naik:
$S_{naik}=\frac{hr}{1-r}$ maka:
$S_{naik}=\frac{\frac{5}{2}.\frac{3}{5}}{1-\frac{3}{5}}=\frac{\frac{3}{2}}{\frac{2}{5}}=\frac{3}{2}\times \frac{5}{2}=\frac{15}{4}$
Panjang seluruh lintasan hingga bola berhenti adalah:
= $S_{turun}+S_{naik}$
= $\frac{25}{4}+\frac{15}{4}$
= 10 meter
Jawaban: D
Cara alternatif (smart solution):
Jika bola dijatuhkan dari ketinggian $h=2,5=\frac{5}{2}$ dan memantul $\frac{p}{q}=\frac{3}{5}$ dari tinggi sebelumnya, maka panjang lintasan bola hingga berhenti adalah:
= $h\times \frac{q+p}{q-p}$
= $\frac{5}{2}\times \frac{5+3}{5-3}$
= 10 meter
Jawaban: D
Soal No. 15
Diketahui deret $\sin x+\cos x\sin x+{{\cos }^{2}}x\sin x+...$. Jika $0 <x <\pi $ maka jumlah deret tersebut sama dengan ….A. $\sin x$
B. $\frac{1+\cos x}{\sin x}$
C. $\tan \frac{1}{2}x$
D. $\frac{\sin x}{1+\cos x}$
E. $\cos x$
Penyelesaian: Lihat/Tutup
$a=\sin x$$r=\frac{U_2}{U_1}=\frac{\cos x\sin x}{\sin x}=\cos x$
$S_{\infty }=\frac{a}{1-r}$ maka:
$\begin{align}S_{\infty } &= \frac{\sin x}{1-\cos x} \\ &= \frac{\sin x}{1-\cos x}\times \frac{1+\cos x}{1+\cos x} \\ &= \frac{\sin x(1+\cos x)}{1-{{\cos }^{2}}x} \\ &= \frac{\sin x(1+\cos x)}{{{\sin }^{2}}x} \\ S_{\infty } &= \frac{1+\cos x}{\sin x} \end{align}$
Jawaban: B
Soal No. 16
Pada segitiga samasisi ABC yang sisi-sisinya a, digambarkan titik-titik A, B dan C berturut-turut titik tengah BC, CA dan AB sehingga terjadi segitiga ABC. Proses semacam ini dikerjakan pada segitiga ABC sehingga diperoleh segitiga ABC dan seterusnya. Maka jumlah luas segitiga ABC, ABC, ABC … dan seterusnya adalah ….
A. $\frac{4}{3}a^2\sqrt{3}$
B. $\frac{3}{4}a^2\sqrt{3}$
C. $\frac{1}{4}a^2\sqrt{3}$
D. $\frac{1}{3}a^2\sqrt{3}$
E. $\frac{2}{3}a^2\sqrt{3}$
Penyelesaian: Lihat/Tutup
Ingat, Luas segitiga sama sisi = $\frac{1}{4}s\sqrt{3}$ maka:Luas ABC = $\frac{1}{4}a^2\sqrt{3}$
Luas A'B'C' = $\frac{1}{4}$Luas ABC = $\frac{1}{16}a^2\sqrt{3}$
Luas A"B"C" = $\frac{1}{4}$Luas A’B’C’ = $\frac{1}{64}a^2\sqrt{3}$
Jadi, luas ABC + luas A'B'C' + luas A"B"C" + … adalah:
= $\frac{1}{4}s\sqrt{3}$ + $\frac{1}{16}a^2\sqrt{3}$ + $\frac{1}{64}a^2\sqrt{3}$ + …
Jumlah luas segitiga membentuk deret geometri tak hingga dengan $U_1=\frac{1}{4}a^2\sqrt{3}$ dan $r=\frac{1}{4}$ yang jumlahnya adalah:
= $\frac{U_1}{1-r}$
= $\frac{\frac{1}{4}a^2\sqrt{3}}{1-\frac{1}{4}}$
= $\frac{\frac{1}{4}a^2\sqrt{3}}{\frac{3}{4}}$
= $\frac{1}{4}a^2\sqrt{3}\times \frac{4}{3}$
= $\frac{1}{3}a^2\sqrt{3}$
Jawaban: D
Soal No. 17
Bujur sangkar yang terjadi seperti pada gambar di samping jika diteruskan jumlah luasnya adalah ….
A. $2a^2$
B. $3a^2$
C. $4a^2$
D. $5a^2$
E. $\infty $
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Luas ABCD = $a^2$
Luas EFGH = $\frac{1}{2}$ x luas EFGH
Luas EFGH = $\frac{1}{2}a^2$
Perhatikan gambar berikut!

Luas IJKL = $\frac{1}{2}$Luas segitiga EFGH
Luas IJKL = $\frac{1}{2}\times \frac{1}{2}a^2$ = $\frac{1}{4}a^2$
Jumlah luas persegi yang terbentuk jika diteruskan akan membentuk deret geometri tak hingga yaitu: $a+\frac{1}{2}a^2+\frac{1}{4}a^2+...$ dengan $U_1=a^2$ dan $r=\frac{1}{2}$.
Jumlah seluruhnya:
= $\frac{U_1}{1-r}$ = $\frac{a^2}{1-\frac{1}{2}}$ = $\frac{a^2}{\frac{1}{2}}$ = $2a^2$
Jawaban: A
Soal No. 18
Jika $(x-50)$, $(x-14)$, $(x-5)$ adalah tiga suku pertama suatu deret geometri tak hingga, maka jumlah semua suku-sukunya adalah ….A. $-96$
B. $-64$
C. $-36$
D. $-24$
E. $-12$
Penyelesaian: Lihat/Tutup
Barisan geometri tak hingga:$(x-50)$, $(x-14)$, $(x-5)$
Syarat barisan geometri:
$\begin{align}\frac{U_2}{U_1} &= \frac{U_3}{U_2} \\ \frac{x-14}{x-50} &= \frac{x-5}{x-14} \\ (x-14)(x-14) &= (x-50)(x-5) \\ x^2-28x+196 &= x^2-55x+250 \\ -28x+196 &= -55x+250 \\ -28x+55x &= 250-196 \\ 27x &= 54 \\ x &= \frac{54}{27} \\ x &= 2 \end{align}$
$\begin{align}a &= x-50 \\ &= 2-50 \\ a &= -48 \end{align}$
$\begin{align}U_2 &= x-14 \\ &= 2-14 \\ U_2 &= -12 \end{align}$
$r=\frac{U_2}{U_1}=\frac{x-14}{x-50}=\frac{2-14}{2-50}=\frac{-12}{-48}r=\frac{1}{4}$
jumlah semua suku-sukunya adalah:
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{-48}{1-\frac{1}{4}}=\frac{-48}{\frac{3}{4}}=-48\times \frac{4}{3}=-64$
Jawaban: B
Soal No. 19
Deret ukur tak hingga: $(x-1)$, $(x-1)^2$, $(x-1)^3$ , … konvergen (jumlahnya ada) untuk nilai-nilai $x$ dalam selang ….A. $-1 <x <1$
B. $0 <x <2$
C. $2 <x <\infty $
D. $-\infty <x <2$
E. $-\infty <x <\infty $
Penyelesaian: Lihat/Tutup
Syarat deret konvergen:$\begin{align}\left| r \right| & <1 \\ \left| \frac{U_2}{U_1} \right| & < 1 \end{align}$
$\left| \frac{(x-1)^2}{x-1} \right| < 1$
$\left| x-1 \right| < 1$
$-1 < x-1 < 1$
$-1+1 < x-1+1 < 1+1$
$0 < x < 2$
Jawaban: B
Soal No. 20
Deret ukur $1{{+}^{2}}\log (x-3){{+}^{2}}{{\log }^{2}}(x-3)+...$ konvergen jika ….A. $3\frac{1}{2} < x < 5$
B. $3\frac{1}{2}\le x\le 5$
C. $0\le \left| x-3 \right|\le 2$
D. $0 < \left| x-3 \right|\le 2$
E. $0 < \left| x-3 \right| < 2$
Penyelesaian: Lihat/Tutup
Syarat deret konvergen:$-1 < r < 1$
$-1 < \frac{U_2}{U_1} < 1$
$-1 < \frac{^{2}\log (x-3)}{1} < 1$
$-1{{ < }^{2}}\log (x-3) < 1$
$^{2}\log {{2}^{-1}}{{ < }^{2}}\log (x-3){{ < }^{2}}\log 2$
${{2}^{-1}} < x-3 < 2$
$\frac{1}{2} < x-3 < 2$
$\frac{1}{2}+3 < x-3+3 < 2+3$
$3\frac{1}{2} < x < 5$
Jawaban: A
Soal No. 21
Jumlah tak hingga deret geometri $4+1+\frac{1}{4}+\frac{1}{16}+...$ adalah ….A. $\frac{4}{3}$
B. $\frac{5}{3}$
C. $\frac{12}{3}$
D. $\frac{15}{3}$
E. $\frac{16}{3}$
Penyelesaian: Lihat/Tutup
$4+1+\frac{1}{4}+\frac{1}{16}+...$$a=4$ dan $r=\frac{U_2}{U_1}=\frac{1}{4}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{4}{1-\frac{1}{4}}=\frac{4}{\frac{3}{4}}=4\times \frac{4}{3}=\frac{16}{3}$
Jawaban: E
Soal No. 22
Jumlah tak hingga deret geometri: $64+8+1+\frac{1}{8}+...$ adalah ….A. $74\frac{1}{7}$
B. $74\frac{1}{8}$
C. 74
D. $73\frac{1}{7}$
E. $73\frac{1}{8}$
Penyelesaian: Lihat/Tutup
$64+8+1+\frac{1}{8}+...$$a=64$ dan $r=\frac{U_2}{U_1}=\frac{8}{64}=\frac{1}{8}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{64}{1-\frac{1}{8}}=\frac{4}{\frac{7}{8}}=64\times \frac{8}{7}=\frac{512}{7}=73\frac{1}{7}$
Jawaban: D
Soal No. 23
Jumlah deret geometri tak hingga $18+6+2+\frac{2}{3}+...$ adalah ….A. $26\frac{2}{3}$
B. 27
C. 36
D. $38\frac{7}{6}$
E. 54
Penyelesaian: Lihat/Tutup
$18+6+2+\frac{2}{3}+...$$a=18$ dan $r=\frac{U_2}{U_1}=\frac{6}{18}=\frac{1}{3}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{18}{1-\frac{1}{3}}=\frac{18}{\frac{2}{3}}=18\times \frac{3}{2}=27$
Jawaban: B
Soal No. 24
Diketahui deret geometri $4+2+1+\frac{1}{2}+...$ jumlah tak hingga deret tersebut adalah ….A. $\infty $
B. 9
C. $8\frac{1}{2}$
D. 8
E. $7\frac{3}{4}$
Penyelesaian: Lihat/Tutup
$4+2+1+\frac{1}{2}+...$$a=4$ dan $r=\frac{U_2}{U_1}=\frac{2}{4}=\frac{1}{2}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{4}{1-\frac{1}{2}}=\frac{4}{\frac{1}{2}}=4\times \frac{2}{1}=8$
Jawaban: D
Soal No. 25
Jumlah tak hingga deret geometri: $6+3+\frac{3}{2}+\frac{3}{4}+...$ adalah …A. 10
B. 11
C. 12
D. 13
E. 14
Penyelesaian: Lihat/Tutup
$6+3+\frac{3}{2}+\frac{3}{4}+...$$a=6$ dan $r=\frac{U_2}{U_1}=\frac{3}{6}=\frac{1}{2}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{6}{1-\frac{1}{2}}=\frac{6}{\frac{1}{2}}=6\times \frac{2}{1}=12$
Jawaban: C
Soal No. 26
Jumlah deret geometri tak hingga: $\sqrt{2}+1+\frac{1}{2}\sqrt{2}+\frac{1}{2}+...$ adalah ….A. $\frac{2}{3}\left( \sqrt{2}+1 \right)$
B. $\frac{3}{2}\left( \sqrt{2}+1 \right)$
C. $2\left( \sqrt{2}+1 \right)$
D. $3\left( \sqrt{2}+1 \right)$
E. $4\left( \sqrt{2}+1 \right)$
Penyelesaian: Lihat/Tutup
$\sqrt{2}+1+\frac{1}{2}\sqrt{2}+\frac{1}{2}+...$$a=\sqrt{2}$ dan $r=\frac{U_2}{U_1}=\frac{1}{\sqrt{2}}$
$S_{\infty }=\frac{a}{1-r}$ maka:
$\begin{align}S_{\infty } &= \frac{\sqrt{2}}{1-\frac{1}{\sqrt{2}}} \\ &= \frac{\sqrt{2}}{\frac{\sqrt{2}-1}{\sqrt{2}}} \\ &= \sqrt{2}\times \frac{\sqrt{2}}{\sqrt{2}-1} \\ &= \frac{2}{\sqrt{2}-1}\times \frac{\sqrt{2}+1}{\sqrt{2}+1} \\ S_{\infty } &= 2(\sqrt{2}+1) \end{align}$
Jawaban: C
Soal No. 27
Jika suku pertama deret geometri tak hingga adalah 1, sedangkan jumlah suku-suku yang bernomor ganjil = 2, maka jumlah deret dengan rasio yang positif adalah …A. $2+\sqrt{2}$
B. $2-\sqrt{2}$
C. $-2-\sqrt{2}$
D. $-2+\sqrt{2}$
E. $2+\sqrt{3}$
Penyelesaian: Lihat/Tutup
$a=1$, $S_{ganjil}=2$ maka $S_{\infty }$ = …?Ingat, $S_{ganjil}=\frac{a}{1-r^2}$ maka:
$\begin{align}S_{ganjil} &= 2 \\ \frac{a}{1-r^2} &= 2 \\ \frac{1}{1-r^2} &= 2 \\ 1 &= 2-2r^2 \\ 2r^2 &= 1 \\ r^2 &= \frac{1}{2} \\ r &= \frac{1}{\sqrt{2}} \end{align}$
$\begin{align}S_{\infty } &= \frac{a}{1-r} \\ &= \frac{1}{1-\frac{1}{\sqrt{2}}} \\ &= \frac{1}{\frac{\sqrt{2}-1}{\sqrt{2}}} \\ &= \frac{\sqrt{2}}{\sqrt{2}-1}\times \frac{\sqrt{2}+1}{\sqrt{2}+1} \\ &= \frac{2+\sqrt{2}}{2-1} \\ S_{\infty } &= 2+\sqrt{2} \end{align}$
Jawaban: A
Soal No. 28
Sebuah bola pingpong dijatuhkan ke lantai dari ketinggian 2 meter. Setiap kali setelah bola memantul ia mencapai ketinggian tiga per empat dari ketinggian yang dicapai sebelumnya. Panjang lintasan bola tersebut dari pantulan ke-3 sampai ia berhenti adalah …A. 3,38 meter
B. 3,75 meter
C. 4,25 meter
D. 6,75 meter
E. 7,75 meter
Penyelesaian: Lihat/Tutup
Perhatikan gambar berikut!
Panjang lintasan bola tersebut dari pantulan ke-3 sampai ia berhenti adalah dua kali jumlah deret geometri tak hingga dengan $a=\frac{27}{32}$ dan $r=\frac{3}{4}$.
$\begin{align}2\times S_{\infty } &= 2.\frac{a}{1-r} \\ &= 2.\frac{\frac{27}{32}}{1-\frac{3}{4}} \\ &= \frac{2.\frac{27}{32}}{\frac{1}{4}} \\ &= \frac{27}{16}\times \frac{4}{1} \\ &= \frac{27}{4} \\ &= 6,75 \end{align}$
Jadi, panjang lintasan bola tersebut dari pantulan ke-3 sampai ia berhenti adalah 6,75 meter.
Jawaban: D
Soal No. 29
Sebuah bola jatuh dari ketinggian 10 m dan memantul kembali dengan ketinggian $\frac{3}{4}$ kali tinggi sebelumnya. Pemantulan ini berlangsung terus menerus hingga bola berhenti. Jumlah seluruh lintasan bola adalah ….A. 60 m
B. 70 m
C. 80 m
D. 90 m
E. 100 m
Penyelesaian: Lihat/Tutup
Bola dijatuhkan dari ketinggian (h) = 10 meter dan memantul dengan r = $\frac{3}{4}$Panjang lintasan bola turun:
$S_{turun}=\frac{h}{1-r}$ maka:
$S_{turun}=\frac{10}{1-\frac{3}{4}}=\frac{10}{\frac{1}{4}}=10\times \frac{4}{1}=40$
Panjang lintasan bola naik:
$S_{naik}=\frac{hr}{1-r}$ maka:
$S_{naik}=\frac{10.\frac{3}{4}}{1-\frac{3}{4}}=\frac{\frac{15}{2}}{\frac{1}{4}}=\frac{15}{2}\times \frac{4}{1}=30$
Panjang seluruh lintasan hingga bola berhenti adalah:
= $S_{turun}+S_{naik}$
= 40 + 30
= 70 meter
Jawaban: B
Cara alternatif (smart solution):
Jika bola dijatuhkan dari ketinggian $h=10$ meter dan memantul $\frac{p}{q}=\frac{3}{4}$ dari tinggi sebelumnya, maka panjang lintasan bola hingga berhenti adalah:
= $h\times \frac{q+p}{q-p}$
= $10\times \frac{4+3}{4-3}$
= 70 meter
Jawaban: B
Soal No. 30
Sebuah bola dijatuhkan vertikal dari ketinggian 6 m terjadi pantulan ke-2,ke-3,ke-4 dan seterusnya dengan ketinggian 4 m, $\frac{8}{3}$ m, $\frac{16}{9}$ m dan seterusnya. Jarak lintasan yang ditempuh bola sampai berhenti ….A. 16 m
B. 18 m
C. 20 m
D. 24 m
E. 30 m
Penyelesaian: Lihat/Tutup
Bola dijatuhkan dari ketinggian (h) = 6 meter.Rasio pantulan bola adalah:
$r=\frac{\frac{8}{3}}{4}=\frac{8}{3}\times \frac{1}{4}=\frac{2}{3}$
Panjang lintasan bola turun:
$S_{turun}=\frac{h}{1-r}$ maka:
$S_{turun}=\frac{6}{1-\frac{2}{3}}=\frac{6}{\frac{1}{3}}=6\times \frac{3}{1}=18$
Panjang lintasan bola naik:
$S_{naik}=\frac{hr}{1-r}$ maka:
$S_{naik}=\frac{6.\frac{2}{3}}{1-\frac{2}{3}}=\frac{4}{\frac{1}{3}}=4\times \frac{3}{1}=12$
Panjang seluruh lintasan hingga bola berhenti adalah:
= $S_{turun}+S_{naik}$
= 18 + 12
= 30 meter
Jawaban: E
Cara alternatif (smart solution):
Jika bola dijatuhkan dari ketinggian $h=6$ meter dan memantul $\frac{p}{q}=\frac{2}{3}$ dari tinggi sebelumnya, maka panjang lintasan bola hingga berhenti adalah:
= $h\times \frac{q+p}{q-p}$
= $6\times \frac{3+2}{3-2}$
= 30 meter
Jawaban: E
Soal No. 31
Sebuah bola dijatuhkan dari ketinggian 1 meter. Setiap kali sesudah jatuh mengenai lantai, bola itu dipantulkan lagi mencapai tinggi $\frac{3}{4}$ dari tinggi sebelumnya. Maka panjang seluruh jalan yang dilalui bola itu sampai berhenti adalah …A. 2 m
B. 3 m
C. 5 m
D. 7 m
E. 8 m
Penyelesaian: Lihat/Tutup
Bola dijatuhkan dari ketinggian (h) = 1 meter dan memantul dengan r = $\frac{3}{4}$Panjang lintasan bola turun:
$S_{turun}=\frac{h}{1-r}$ maka:
$S_{turun}=\frac{1}{1-\frac{3}{4}}=\frac{1}{\frac{1}{4}}=4$
Panjang lintasan bola naik:
$S_{naik}=\frac{hr}{1-r}$ maka:
$S_{naik}=\frac{1.\frac{3}{4}}{1-\frac{3}{4}}=\frac{\frac{3}{4}}{\frac{1}{4}}=\frac{3}{4}\times \frac{4}{1}=3$
Panjang seluruh lintasan hingga bola berhenti adalah:
= $S_{turun}+S_{naik}$
= 4 + 3
= 7 meter
Jawaban: D
Cara alternatif (smart solution):
Jika bola dijatuhkan dari ketinggian $h=1$ meter dan memantul $\frac{p}{q}=\frac{3}{4}$ dari tinggi sebelumnya, maka panjang lintasan bola hingga berhenti adalah:
= $h\times \frac{q+p}{q-p}$
= $1\times \frac{4+3}{4-3}$
= 7 meter
Jawaban: D
Soal No. 32
$1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\frac{1}{16}-...$ = ….A. $\frac{1}{3}$
B. $\frac{2}{3}$
C. 1
D. $\frac{5}{6}$
E. $\frac{4}{3}$
Penyelesaian: Lihat/Tutup
$a=1$ dan $r=\frac{U_2}{U_1}=\frac{-\frac{1}{2}}{1}=-\frac{1}{2}$$S_{\infty }=\frac{a}{1-r}$ maka:
$S_{\infty }=\frac{1}{1+\frac{1}{2}}=\frac{1}{\frac{3}{2}}=\frac{2}{3}$
Jawaban: B
Soal No. 33
Agar deret geometri $\frac{x-1}{x},\frac{1}{x},\frac{1}{x(x-1)},...$ jumlahnya mempunyai limit, nilai $x$ harus memenuhi ….A. $x > 0$
B. $x < 1$
C. $x > 2$
D. $0 < x < 1$
E. $x < 0$ atau $x > 2$
Penyelesaian: Lihat/Tutup
$r=\frac{U_2}{U_1}=\frac{\frac{1}{x}}{\frac{x-1}{x}}=\frac{1}{x-1}$Syarat deret geometri konvergen:
$\begin{align}\left| r \right| & < 1 \\ \left| \frac{1}{x-1} \right| & < 1 \\ \left| x-1 \right| & > 1 \end{align}$
$x-1 < -1$ atau $x-1 >1$ maka:
$x < 0$ atau $x >2$
Jawaban: E
Soal No. 34
Jika $r$ rasio (pembanding) suatu deret geometrik tak hingga yang konvergen dan S jumlah deret geometrik tak hingga $\frac{1}{3+r}+\frac{1}{{{(3+r)}^{2}}}+\frac{1}{{{(3+r)}^{3}}}+...$A. $\frac{1}{4} < S < \frac{1}{2}$
B. $\frac{3}{8} < S < \frac{3}{4}$
C. $\frac{1}{3} < S < 1$
D. $\frac{3}{4} < S < \frac{4}{3}$
E. $\frac{1}{5} < S < \frac{4}{5}$
Penyelesaian: Lihat/Tutup
$\frac{1}{3+r}+\frac{1}{{{(3+r)}^{2}}}+\frac{1}{{{(3+r)}^{3}}}+...$$S=\frac{a}{1-r}$ maka:
$\begin{align}S &= \frac{\frac{1}{3+r}}{1-\frac{1}{3+r}} \\ &= \frac{\frac{1}{3+r}}{\frac{3+r-1}{3+r}} \\ &= \frac{1}{3+r}\times \frac{3+r}{2+r} \\ S &= \frac{1}{r+2} \\ r+2 &= \frac{1}{S} \\ r &= \frac{1}{S}-2 \\ r &= \frac{1-2S}{S} \end{align}$
Syarat deret geometri tak hingga:
$\begin{align}\left| r \right| & < 1 \\ \left| \frac{1-2S}{S} \right| & < 1 \\ \frac{\left| 1-2S \right|}{\left| S \right|} & < 1 \\ \left| 1-2S \right| & < \left| S \right| \\ (1-2S+S)(1-2S-S) & < 0 \\ (1-S)(1-3S) & < 0 \end{align}$
$1-S=0\to S=1$
$1-3S=0\to S=\frac{1}{3}$
Jadi, $\frac{1}{3} < S < 1$.
Jawaban: C
Soal No. 35
Untuk $0 < x < \frac{\pi }{2}$, maka jumlah deret tak berhingga $\cos x+\cos x\sin x+\cos x{{\sin }^{2}}x+...$ adalah ….A. $\frac{\cos x+\sin x}{\sin x}$
B. $\frac{1+\cos x}{\sin x}$
C. $\frac{\sin x}{1+\cos x}$
D. $\frac{1+\sin x}{\cos x}$
E. $\frac{\cos x}{1+\sin x}$
Penyelesaian: Lihat/Tutup
$\cos x+\cos x\sin x+\cos x{{\sin }^{2}}x+...$$a=\cos x$ dan $r=\frac{U_2}{U_1}=\frac{\cos x\sin x}{\cos x}=\sin x$
$S_{\infty }=\frac{a}{1-r}$ maka:
$\begin{align}S_{\infty } &= \frac{\cos x}{1-\sin x} \\ &= \frac{\cos x}{1-\sin x}\times \frac{1+\sin x}{1+\sin x} \\ &= \frac{\cos x(1+\sin x)}{1-{{\sin }^{2}}x} \\ &= \frac{\cos x(1+\sin x)}{{{\cos }^{2}}x} \\ S_{\infty } &= \frac{1+\sin x}{\cos x} \end{align}$
Jawaban: D
Soal No. 36
Jumlah suku-suku yang nomor ganjil pada suatu deret ukur tak berhingga adalah 4. Kalau deret itu sendiri jumlahnya = 6, maka deret itu adalah …A. 3, $\frac{3}{4}$, $\frac{3}{16}$, …
B. 3, $\frac{3}{8}$, $\frac{3}{64}$, …
C. 3, $\frac{3}{2}$, $\frac{3}{4}$, …
D. $\frac{3}{8}$, $\frac{3}{4}$, $\frac{3}{2}$, 3, …
E. $\frac{3}{8}$, $\frac{3}{6}$, $\frac{3}{2}$, …
Penyelesaian: Lihat/Tutup
Deret geometri tak berhingga:$S_{ganjil}=4$ dan $S_{\infty }=6$
$S_{genap}=S_{\infty }-S_{ganjil}=6-4=2$
$r=\frac{S_{genap}}{S_{ganjil}}=\frac{2}{4}=\frac{1}{2}$
$\begin{align}S_{\infty } &= 6 \\ \frac{a}{1-r} &= 6 \\ a &= 6-6r \\ a &= 6-6.\frac{1}{2} \\ a &= 3 \end{align}$
Deret geometri tersebut adalah:
$a$, $ar$, $ar^2$, …
3, $\frac{3}{2}$, $\frac{3}{4}$, ….
Jawaban: C
Soal No. 37
Jumlah tak hingga suatu deret geometri adalah 8 dan jumlah semua suku pada kedudukan (urutan) genap adalah $\frac{8}{3}$. Suku kelima deret tersebut adalah …A. 2
B. 1
C. $\frac{1}{2}$
D. $\frac{1}{3}$
E. $\frac{1}{4}$
Penyelesaian: Lihat/Tutup
Deret geometri tak hingga:$S_{\infty }=8$ dan $S_{genap}=\frac{8}{3}$ maka $U_5$ = …
$\begin{align}S_{\infty } &= 8 \\ \frac{a}{1-r} &= 8 \\ a &= 8-8r \end{align}$
Ingat, $S_{genap}=\frac{ar}{1-r^2}$ maka:
$\begin{align}S_{genap} &= \frac{8}{3} \\ \frac{ar}{1-r^2} &= \frac{8}{3} \\ 3ar &= 8-8r^2 \\ 3(8-8r)r &= 8-8r^2 \\ 24r-24r^2 &= 8-8r^2 \\ -16r^2+24r-8 &= 0 \\ 2r^2-3r+1 &= 0 \\ (2r-1)(r-1) &= 0 \end{align}$
$2r-1=0\to r=\frac{1}{2}$
$r-1=0\to r=1$
Karena $-1 < r < 1$ maka $r=\frac{1}{2}$.
$\begin{align}S_{\infty } &= 8 \\ \frac{a}{1-r} &= 8 \\ \frac{a}{1-\frac{1}{2}} &= 8 \\ a &= 4 \end{align}$
Ingat, $U_n=ar^{n-1}$ maka:
$U_5=a{{r}^{4}}=4.{{\left( \frac{1}{2} \right)}^{4}}=\frac{1}{4}$
Jawaban: E

Post a Comment for "Soal Deret Geometri Tak Hingga dan Pembahasan"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.