P2. Menentukan Nilai Suku Banyak
Pada postingan ini kita akan membahas Bagaimana Cara Menentukan Nilai Suku Banyak (Polinomial).
COntoh 1.
Tentukan nilai suku banyak $f(x)=4x^3-7x+5$ untuk $x=3$.
Penyelesaian:
$\begin{align}f(x) &= 4x^3-7x+5 \\ f(3) &= 4.3^3-7.3+5 \\ &= 4.27-21+5 \\ &= 108-16 \\ f(3) &= 92 \end{align}$
Jadi, nilai suku banyak $f(x)=4x^3-7x+5$ untuk $x=3$ adalah $f(3)=92$.
COntoh 2.
Tentukan nilai suku banyak $f(x)=2x^4-5x^2-7x+1$ untuk $x=-2$.
Penyelesaian:
$\begin{align}f(x) &= 2x^4-5x^2-7x+1 \\ f(-2) &= 2(-2)^4-5(-2)^2-7(-2)+1 \\ &= 2.16-5.4+14+1 \\ &= 32-20+15 \\ f(-2) &= 27 \end{align}$
Jadi, nilai suku banyak $f(x)=2x^4-5x^2-7x+1$ untuk $x=-2$ adalah $f(-2)=27$.
COntoh 3.
Tentukanlah nilai $m$ agar suku banyak $x^5+4mx-4{{m}^{2}}$ bernilai 0 untuk $x=2$.
Penyelesaian:
$x^5+4mx-4{{m}^{2}}$ bernilai 0 untuk $x=2$ maka:
$\begin{align}2^5+4m.2-4m^2 &= 0 \\ -4m^2+8m+32 &= 0 \\ m^2-2m-8 &= 0 \\ (m+2)(m-4) &= 0 \end{align}$
$m+2=0\to m=-2$
$m-4=0\to m=4$
Jadi, nilai $m$ agar suku banyak $x^5+4mx-4m^2$ bernilai 0 untuk $x=2$ adalah $m=-2$ atau $m=4$.
Contoh 1.
Tentukan nilai suku banyak $f(x)=32x^5+8x^4-2x^2+3$ untuk $x=\frac{1}{2}$ menggunakan skema horner.
Penyelesaian:
$f(x)=32x^5+8x^4-2x^2+3$
$f(x)=32x^5+8x^4+0x^3-2x^2+0x+3$
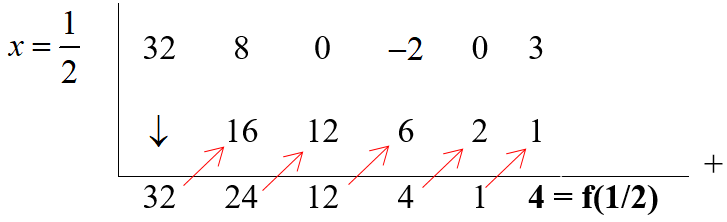
Tanda $\nearrow $ artinya kalikan dengan $\frac{1}{2}$.
Jadi, nilai suku banyak $f(x)=32x^5+8x^4-2x^2+3$untuk $x=2$ adalah $f(2)=4$.
Contoh 2.
Tentukan nilai suku banyak $f(x)=x^4-10x^3+8x-3$ untuk $x=10$ menggunakan skema horner.
Penyelesaian:
$f(x)=x^4-10x^3+8x-3$
$f(x)=x^4-10x^3+0x^2+8x-3$

Tanda $\nearrow $ artinya kalikan dengan 10.
Jadi, nilai suku banyak $f(x)=x^4-10x^3+8x-3$ untuk $x=10$ adalah $f(10)=77$.
A. Menentukan Nilai Suku Banyak dengan Substitusi
Nilai suku banyak $f(x)$ untuk $x=k$ ditulis $f(k)$ yaitu dengan melakukan substitusi nilai $k$ ke dalam variabel-variabel $x$ pada suku banyak tertentu.
Nilai suku banyak $f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$ untuk $x=k$ dengan menggunakan metode substitusi diperoleh:
$f(k)=a_nk^n+a_{n-1}k^{n-1}+...+a_1k+a_0$
Nilai suku banyak $f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$ untuk $x=k$ dengan menggunakan metode substitusi diperoleh:
$f(k)=a_nk^n+a_{n-1}k^{n-1}+...+a_1k+a_0$
COntoh 1.
Tentukan nilai suku banyak $f(x)=4x^3-7x+5$ untuk $x=3$.
Penyelesaian:
$\begin{align}f(x) &= 4x^3-7x+5 \\ f(3) &= 4.3^3-7.3+5 \\ &= 4.27-21+5 \\ &= 108-16 \\ f(3) &= 92 \end{align}$
Jadi, nilai suku banyak $f(x)=4x^3-7x+5$ untuk $x=3$ adalah $f(3)=92$.
COntoh 2.
Tentukan nilai suku banyak $f(x)=2x^4-5x^2-7x+1$ untuk $x=-2$.
Penyelesaian:
$\begin{align}f(x) &= 2x^4-5x^2-7x+1 \\ f(-2) &= 2(-2)^4-5(-2)^2-7(-2)+1 \\ &= 2.16-5.4+14+1 \\ &= 32-20+15 \\ f(-2) &= 27 \end{align}$
Jadi, nilai suku banyak $f(x)=2x^4-5x^2-7x+1$ untuk $x=-2$ adalah $f(-2)=27$.
COntoh 3.
Tentukanlah nilai $m$ agar suku banyak $x^5+4mx-4{{m}^{2}}$ bernilai 0 untuk $x=2$.
Penyelesaian:
$x^5+4mx-4{{m}^{2}}$ bernilai 0 untuk $x=2$ maka:
$\begin{align}2^5+4m.2-4m^2 &= 0 \\ -4m^2+8m+32 &= 0 \\ m^2-2m-8 &= 0 \\ (m+2)(m-4) &= 0 \end{align}$
$m+2=0\to m=-2$
$m-4=0\to m=4$
Jadi, nilai $m$ agar suku banyak $x^5+4mx-4m^2$ bernilai 0 untuk $x=2$ adalah $m=-2$ atau $m=4$.
B. Menentukan Nilai Suku Banyak Menggunakan Skema Horner
Misalkan suku banyak $f(x)=ax^3+bx^2+cx+d$. Nilai suku banyak $f(x)$ untuk $x=k$ dapat ditentukan dengan menggunakan operasi perkalian dan operasi penjumlahan yang disajikan dalam model skema (bagan).

Tanda $\nearrow $ artinya kalikan dengan $k$.
Jadi, nilai suku banyak untuk $x=k$ adalah $f(x)=ak^3+bk^2+ck+d$.
Cara yang digunakan untuk menghitung nilai suku banyak tersebut dinamakan skema horner.

Tanda $\nearrow $ artinya kalikan dengan $k$.
Jadi, nilai suku banyak untuk $x=k$ adalah $f(x)=ak^3+bk^2+ck+d$.
Cara yang digunakan untuk menghitung nilai suku banyak tersebut dinamakan skema horner.
Contoh 1.
Tentukan nilai suku banyak $f(x)=32x^5+8x^4-2x^2+3$ untuk $x=\frac{1}{2}$ menggunakan skema horner.
Penyelesaian:
$f(x)=32x^5+8x^4-2x^2+3$
$f(x)=32x^5+8x^4+0x^3-2x^2+0x+3$
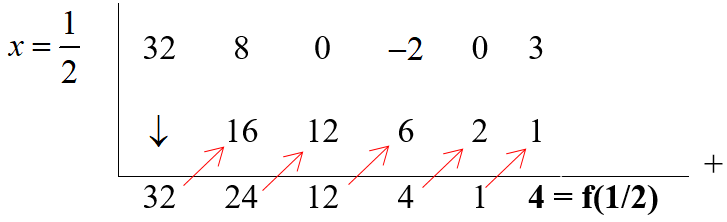
Tanda $\nearrow $ artinya kalikan dengan $\frac{1}{2}$.
Jadi, nilai suku banyak $f(x)=32x^5+8x^4-2x^2+3$untuk $x=2$ adalah $f(2)=4$.
Contoh 2.
Tentukan nilai suku banyak $f(x)=x^4-10x^3+8x-3$ untuk $x=10$ menggunakan skema horner.
Penyelesaian:
$f(x)=x^4-10x^3+8x-3$
$f(x)=x^4-10x^3+0x^2+8x-3$

Tanda $\nearrow $ artinya kalikan dengan 10.
Jadi, nilai suku banyak $f(x)=x^4-10x^3+8x-3$ untuk $x=10$ adalah $f(10)=77$.
C. Soal Latihan
- Dengan cara substitusi tentukan nilai $f(x)=4x^4-3x+8$ untuk $x=-3$.
- Tentukan nilai $m$ agar suku banyak $x^3-mx^2+3x+2$ bernilai $-3$ untuk $x=1$.
- Diketahui $g(x)=x^5+mx^4-2x^3+x+1$ dan $g(2)=3$. Tentukan nilai $g(-2)$.
- Dengan menggunakan skema horner tentukan nilai suku banyak $f(x)=5x^4-x^3+3x-6$ untuk $x=2$.
- Dengan menggunakan skema horner tentukan $f(-4)$ jika $f(x)=2x^4-8x^2+10$

Post a Comment for "P2. Menentukan Nilai Suku Banyak"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.