Polinomial 3. Pembagian Suku Banyak (Bersusun dan Horner-Kino)

Misalkan suku banyak $f(x)$ dibagi dengan $P(x)$ memberikan hasil bagi $H(x)$ dan sisa $S(x)$, maka diperoleh:
$f(x)=P(x).H(x)+S(x)$
atau
$\text{yang dibagi}=\text{pembagi}\times \text{hasil}+\text{sisa}$
Jika $f(x)$ suku banyak berderajat $n$ dan $P(x)$ adalah berderajat $m$, dengan $m\le n$ maka:
1) $H(x)$ berderajat $(n-m)$
2) $S(x)$ berderajat maksimum $(m-1)$.

A. Pembagian Suku Banyak dengan Metode Pembagian Bersusun

Prosedur pembagian suku banyak dengan metode pembagian bersusun sama dengan prosedur pembagian pada bilangan bulat.
Contoh 1.
Tentukan hasil dan sisa pembagian $f(x)=4x^3-10x^2+14x-15$ oleh $(x-5)$.
Penyelesaian:

Jadi, hasil pembagian $H(x)=4x^2+10x+64$ dan sisa pembagian $S(x)=-305$.

---

Contoh 2.
Tentukan hasil dan sisa pembagian $2x^3+7x^2-6x-9$ oleh $2x-1$.
Penyelesaian:

Jadi, hasil pembagian $H(x)=x^2+4x-1$ dan sisa pembagian $S(x)=-10$.

---

Contoh 3.
Tentukan hasil dan sisa pembagian $2x^4-4x^3+3x^2-2x+8$ oleh $x^2+2x+2$.
Penyelesaian:

Jadi, hasil bagi $H(x)=2x^2-8x+15$ dan sisa pembagian $-16x-22$.

---

B. Pembagian Suku Banyak dengan Metode Horner (Pembagian Sintetik)

1. Pembagian Suku Banyak dengan $(x-k)$

Misalkan suku banyak $f(x)=ax^2+bx+c$ dibagi dengan $(x-k)$ memberikan hasil $H(x)$ dan sisa $S$. Untuk menentukan hasil bagi $H(x)$ dan sisa $S(x)$ digunakan pembagian suku banyak dengan cara skematik yang dinamakan strategi pembagian sintetik (strategi Horner) seperti berikut ini:
$(ax^2+bx+c)\div (x-k)$ maka:

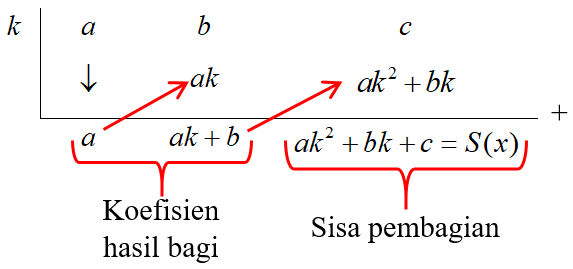
Jadi, hasil bagi $H(x)=ax+(ak+b)$ dan sisa $S(x)=a{{k}^{2}}+bk+c$.

---

Contoh:
Tentukan hasil dan sisa pembagian suku banyak $2x^4-3x^2+x+7$ oleh $(x-3)$.
Penyelesaian:
$(2x^4-3x^2+x+7)\div (x-3)$
Pembagi $(x-3)$ maka $k=3$

Jadi, hasil bagi $H(x)=2x^3+6x^2+15x+46$ dan sisa $S(x)=145$.

---

2. Pembagian Suku Banyak dengan $(ax-b)$

Misalkan $k=\frac{b}{a}$ adalah bilangan rasional, sehingga bentuk $(x-k)$ menjadi $\left( x-\frac{b}{a} \right)$. Jika sukubanyak $f(x)$ dibagi dengan $\left( x-\frac{b}{a} \right)$ memberikan hasil $h(x)$ dan sisa $S(x)$ maka:
$f(x)=\left( x-\frac{b}{a} \right).h(x)+S(x)$
$f(x)=\left( \frac{ax-b}{a} \right).h(x)+S(x)$
$f(x)=(ax-b).\frac{h(x)}{a}+S(x)$
Dari persamaan akhir ini diperoleh: $f(x)$ dibagi $(ax-b)$ memberikan hasil bagi $H(x)=\frac{h(x)}{a}$ dan sisa $S(x)$.

---

Contoh:
Tentukan hasil dan sisa pembagian suku banyak $f(x)=4x^4-3x^3+7x^2-2x+1$ oleh $(4x+1)$.
Penyelesaian:
$f(x)=4x^4-3x^3+7x^2-2x+1$
Pembagi $(4x+1)$maka $k=-\frac{1}{4}$

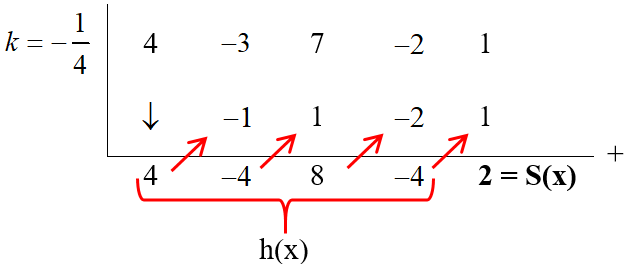
Hasil pembagian adalah:
$\begin{align}H(x) &= \frac{h(x)}{a} \\ &= \frac{4x^3-4x^2+8x-4}{4} \\ H(x) &= x^3-x^2+2x-1 \end{align}$
Sisa pembagian = $S(x)$ = 2.

---

3. Pembagian Suku Banyak dengan $ax^2+bx+c$

Pembagian suku banyak $f(x)$ dengan $ax^2+bx+c$ menggunakan skema horner (pembagian sintetis) dapat dilakukan jika $ax^2+bx+c$ dapat difaktorkan menjadi $a(x-{{k}_{1}})(x-{{k}_{2}})$ dengan $a\ne 0$. Adapun langkah-langkah pembagiannya adalah sebagai berikut:

1. Bagi $f(x)$ dengan $(x-k_1)$, diperoleh: $f(x)=(x-k_1).H_1(x)+S_1$.
2. Hasil bagi $H_1(x)$ dibagi dengan $(x-k_2)$, diperoleh: $H_1(x)=(x-k_2).H_2(x)+S_2$.
3. Substitusi $H_1(x)$ ke persamaan $f(x)$ pada langkah 1, diperoleh:

Kesimpulan:
Jika $f(x)$ dibagi dengan $ax^2+bx+c$ = $a(x-k_1)(x-k_2)$ maka:
1. Hasil bagi = $H(x)$ = $\frac{H_2(x)}{a}$
2. Sisa = $S(x)$ = $S_2(x-k_1)+S_1$

---

Contoh:
Tentukan hasil dan sisa pembagian suku banyak $f(x)=5x^4-x^3+2x^2+8x-3$ oleh $x^2-x-6$.
Penyelesaian:
$f(x)=5x^4-x^3+2x^2+8x-3$
Pembagi:
$(x^2-x-6)=(x-3)(x+2)$ maka $k_1=3$ dan $k_2=-2$

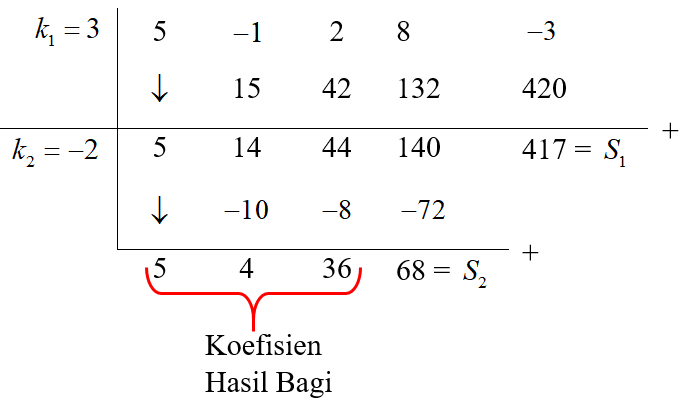
Jadi,
Hasil = $H(x)$ = $5x^2+4x+36$
$\begin{align}\text{Sisa} &= S(x) \\ &= S_2(x-k_1)+S_1 \\ &= 68(x-3)+417 \\ &= 68x-204+417 \\ \text{Sisa} &= 68x+213 \end{align}$

---

C. Pembagian Suku Banyak dengan Metode Horner-Kino

Metode Horner-Kino adalah metode pembagian suku banyak $f(x)$ dengan $ax^2+bx+c$. Pencetus metode ini adalah Bapak Prof. Sukino Suparmin, M.Sc.
Misal suku banyak $f(x)=px^4+qx^3+rx^2+sx+t$ dibagi dengan $ax^2+bx+c$, maka tentukan $k_1=-\frac{c}{a}$ dan $k_2=-\frac{b}{a}$ kemudian ikuti pola Horner-Kino berikut:

---

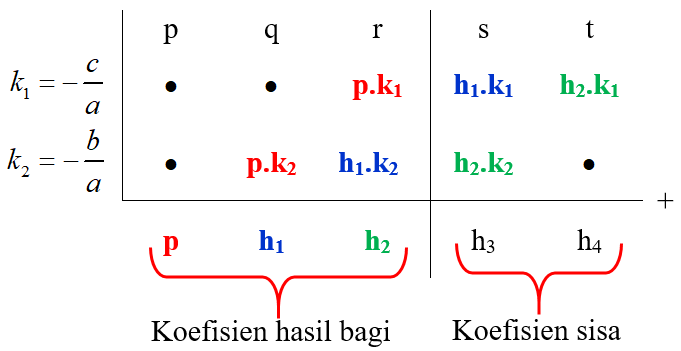
Contoh:
Tentukan hasil dan sisa pembagian $2x^4-4x^3+3x^2-2x+1$ oleh $x^2+2x-4$.
Penyelesaian:
$f(x)=2x^4-4x^3+3x^2-2x+1$
Pembagi $x^2+2x+2$ maka:
$k_1=-\frac{c}{a}=-\frac{-4}{1}=4$
$k_2=-\frac{b}{a}=-\frac{2}{1}=-2$

Jadi,
Hasil bagi $H(x)=2x^2-8x+27$ dan sisa $S(x)=-88x+109$.

---

D. Soal Latihan

1. Tentukan hasil bagi dan sisa pembagian $f(x)=x^3+4x^2-x-4$ oleh $x+4$ menggunakan metode pembagian bersusun.
2. Tentukan hasil bagi dan sisa pembagian $f(x)=3x^4+2x^3-7x^2+5x-2$ oleh $3x-1$ menggunakan metode pembagian sintetik (skema horner).
3. Tentukan hasil bagi dan sisa pembagian $f(x)=x^3+2x^2-8x-2$ oleh $x^2-2x-15$ menggunakan metode pembagian sintetik (skema horner).
4. Tentukan hasil bagi dan sisa pembagian $f(x)=2x^4-5x^3+6x^2-x+4$ oleh $x^2-4x-5$ menggunakan metode pembagian sintetik (skema horner).
5. Tentukan hasil bagi dan sisa pembagian $f(x)=x^3-5x^2+2$ oleh $x^2+4x-1$ menggunakan metode horner-kino.

Semoga postingan: Polinomial 3. Pembagian Suku Banyak (Bersusun dan Horner-Kino) ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :