Soal Ukuran Penyebaran Data Tunggal - Simpangan Kuartil - Simpangan Rata-rata - Simpangan Baku - Varians dan Pembahasan
Hallo...! Pengunjung setia Catatan Matematika, kali ini Bang RP (Reikson Panjaitan, S.Pd) berbagi Kumpulan Soal Ukuran Penyebaran Data Tunggal dan Pembahasannya. Ayo... manfaatkan website Catatan Matematika ini untuk belajar matematika secara online.
A. 1
B. 2
C. 3,5
D. 4
E. 7
3, 3, 4, 4, 4, 5, 5, 6, 6, 7, 7, 8, 9, 10, 10
$n$ = 15
$\begin{align}Q_1 &= \text{data ke-}\frac{1}{4}(n+1) \\ &= \text{data ke-}\frac{1}{4}(15+1) \\ &= \text{data ke-}4 \\ Q_1 &= 4 \end{align}$
$\begin{align}Q_3 &= \text{data ke-}\frac{3}{4}(n+1) \\ &= \text{data ke-}\frac{3}{4}(15+1) \\ &= \text{data ke-}12 \\ Q_3 &= 8 \end{align}$
Simpangan kuartil ($Q_d$) adalah:
$\begin{align}Q_d &= \frac{1}{2}\left( Q_3-Q_1 \right) \\ &= \frac{1}{2}(8-4) \\ Q_d &= 2 \end{align}$
Jawaban: B
A. 0
B. 3,6
C. 5,6
D. 11
E. 28
$\begin{align}\bar{x} &= \frac{\sum{{{x}_{i}}}}{n};\,\text{untuk}\,i=1,2,3,...,n \\ &= \frac{3+5+13+15+19}{5} \\ \bar{x} &= 11 \end{align}$
Simpangan Rata-rata:

Jawaban: C
A. 1
B. $\frac{7}{3}$
C. 2
D. $\frac{14}{3}$
E. 5
$\bar{x}=\frac{7+2+3+8+4+6}{6}=5$
Varians:

Jawaban: D
A. $\sqrt{15}$
B. $\sqrt{10}$
C. $\sqrt{5}$
D. $\sqrt{3}$
E. $\sqrt{2}$
$\bar{x}=\frac{2+3+4+5+6}{5}=4$
Varians ($S^2$):

Simpangan baku (S):
$S=\sqrt{\operatorname{varians}}=\sqrt{2}$
Jawaban: E
A. rata-rata nilai menjadi 70
B. rata-rata nilai menjadi 65
C. simpangan baku menjadi 20
D. simpangan baku menjadi 5
E. median menjadi 50

Jawaban: C
A. 3
B. 4
C. 7
D. 8
E. 9

$\begin{align}6p &= 9 \\ p &= \frac{9}{6} \\ p &= \frac{3}{2} \end{align}$
$\begin{align}16p-q &= 20 \\ 16.\frac{3}{2}-q &= 20 \\ 24-q &= 20 \\ 24-20 &= q \\ 4 &= q \end{align}$
$2p+q=2.\frac{3}{2}+4=7$
Jawaban: C
A. $\frac{1}{2}\sqrt{11}$
B. $\frac{1}{2}\sqrt{13}$
C. $\frac{1}{2}\sqrt{15}$
D. $\frac{1}{2}\sqrt{17}$
E. $\frac{1}{2}\sqrt{19}$
$\bar{x}=\frac{7+7+6+11+7+5+6+7}{8}=7$
Varians:

Simpangan baku:
$S=\sqrt{\text{varians}}=\sqrt{\frac{11}{4}}=\frac{1}{2}\sqrt{11}$
Jawaban: A
A. 0
B. 2
C. 3,6
D. 5,2
E. 10
$\bar{x}=\frac{4+7+10+14+15}{5}=10$
Simpangan rata-rata:
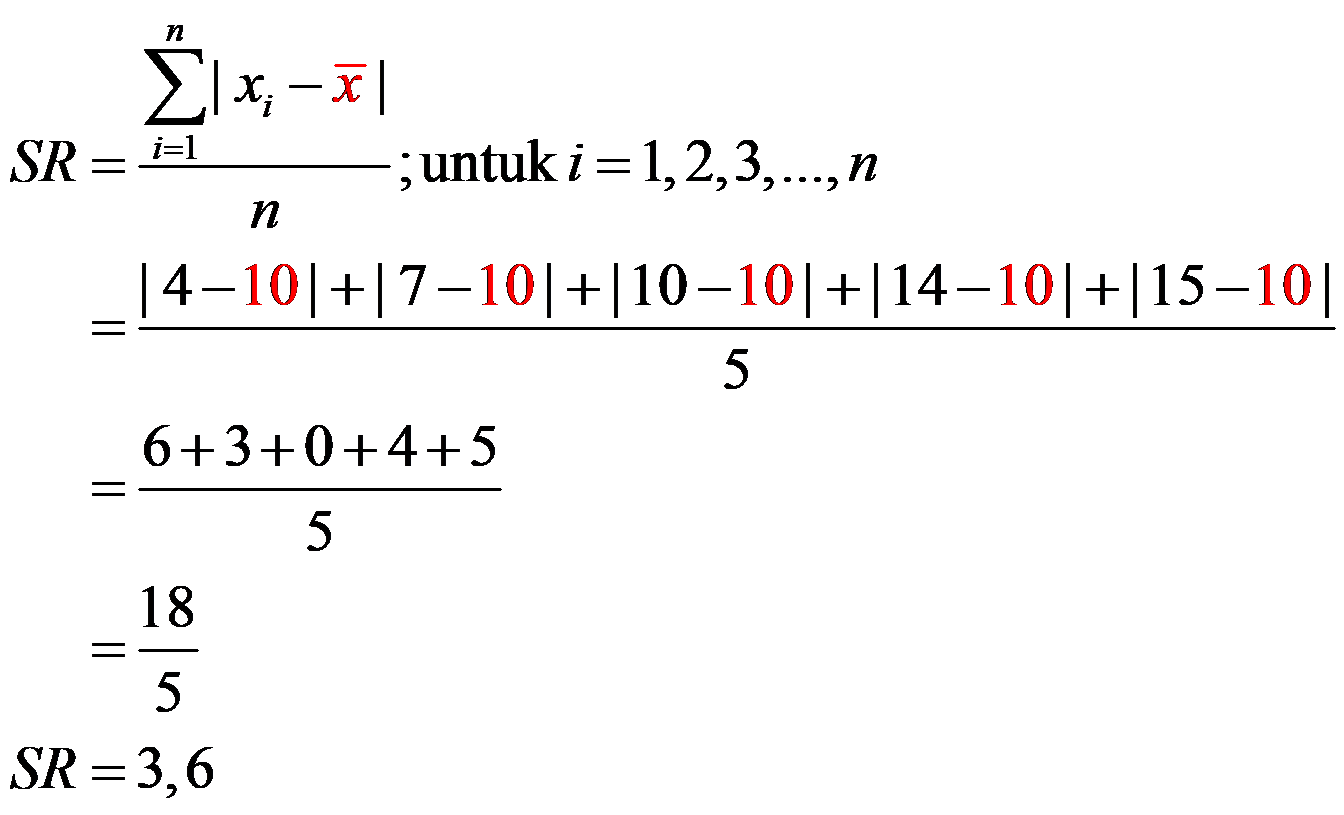
Jawaban: C
A. 1
B. 2
C. 3
D. 4
E. 5

$\begin{align}\bar{x}_{baru} &= S_{baru} \\ 4 &= 2a \\ 2 &= a \end{align}$
Jadi, simpangan baku yang lama adalah ${{S}_{lama}}=a=2$.
Jawaban: B
A. 0
B. 1,8
C. 2
D. 2,8
E. 12
$\begin{align}\bar{x} &= \frac{\sum{{{x}_{i}}}}{n};\,\text{untuk}\,i=1,2,3,...,n \\ &= \frac{7+10+12+15+16}{5} \\ \bar{x} &= 12 \end{align}$
Simpangan Rata-rata:

Jawaban: D
A. $\frac{2}{3}\sqrt{5}$
B. $\frac{2}{3}\sqrt{11}$
C. $2\sqrt{2}$
D. $2\sqrt{5}$
E. $6\sqrt{2}$
$\begin{align}\bar{x} &= \frac{2.20+22+3.24+26+2.28}{9} \\ &= \frac{216}{9} \\ \bar{x} &= 24 \end{align}$
Varians ($S^2$):

Simpangan baku (S):
$\begin{align}S &= \sqrt{\operatorname{varians}} \\ &= \sqrt{8} \\ S &= 2\sqrt{2} \end{align}$
Jawaban: C
A. 18
B. 19
C. 20
D. 21
E. 22
$\begin{align}\bar{x} &= \frac{x_1+15+x_3}{3} \\ 15 &= \frac{x_1+15+x_3}{3} \\ 45 &= x_1+15+x_3 \\ 30 &= x_1+x_3 \end{align}$
$\begin{align}J &= x_3-x_1 \\ 10 &= x_3-x_1 \end{align}$
$30={{x}_{3}}+{{x}_{1}}$
--------------------- +
$\begin{align}40 &= 2x_3 \\ 20 &= x_3 \\ \end{align}$
Jadi, data terbesar adalah 20.
Jawaban: C
A. $\frac{1}{4}\sqrt{3}$
B. $\frac{1}{2}\sqrt{3}$
C. $\frac{1}{3}\sqrt{6}$
D. $\frac{1}{2}\sqrt{6}$
E. $2\sqrt{6}$
$\begin{align}\bar{x} &= \frac{2.6+4+2.5+2.7+8}{8} \\ &= \frac{48}{8} \\ \bar{x} &= 6 \end{align}$
Varians ($S^2$):

Simpangan baku (S):
$\begin{align}S &= \sqrt{\operatorname{varians}} \\ &= \sqrt{\frac{3}{2}} \\ &= \frac{\sqrt{3}}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ S &= \frac{1}{2}\sqrt{6} \end{align}$
Jawaban: D
A. 3
B. 4
C. 5
D. 6
E. 7

$7p=9\to p=\frac{9}{7}$
$\begin{align}35p-q &= 42 \\ 35.\frac{9}{7}-q &= 42 \\ 45-q &= 42 \\ 45-42 &= q \\ 3 &= q \end{align}$
$7p-q=7.\frac{9}{7}-3=6$
Jawaban: D
A. 8
B. 10
C. 12
D. 14
E. 16
$\begin{align}\frac{6}{y} &= 3 \\ 3y &= 6 \\ y &= 2 \end{align}$
$\begin{align}\frac{12-x}{y} &= 2 \\ \frac{12-x}{2} &= 2 \\ 12-x &= 4 \\ -x &= -8 \\ x &= 8 \end{align}$
$x+y=8+2=10$
Jawaban: B
A. rata-rata 76, jangkauan 108
B. rata-rata 76, jangkauan 140
C. rata-rata 76, jangkauan 36
D. rata-rata 108, jangkauan 36
E. rata-rata 108, jangkauan 108

Jawaban: B
Tata Cara Belajar:
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cek jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
Cobalah mengerjakan soal-soal yang tersedia secara mandiri. Setelah itu cek jawaban kamu dengan pembahasan yang telah disediakan, dengan cara:
klik "LIHAT/TUTUP:".
Soal No. 1
Simpangan kuartil dari data 6, 7, 7, 3, 8, 4, 6, 5, 5, 9, 10, 10, 4, 4, 3 adalah ...A. 1
B. 2
C. 3,5
D. 4
E. 7
Penyelesaian: Lihat/Tutup
Data diurutkan menjadi:3, 3, 4, 4, 4, 5, 5, 6, 6, 7, 7, 8, 9, 10, 10
$n$ = 15
$\begin{align}Q_1 &= \text{data ke-}\frac{1}{4}(n+1) \\ &= \text{data ke-}\frac{1}{4}(15+1) \\ &= \text{data ke-}4 \\ Q_1 &= 4 \end{align}$
$\begin{align}Q_3 &= \text{data ke-}\frac{3}{4}(n+1) \\ &= \text{data ke-}\frac{3}{4}(15+1) \\ &= \text{data ke-}12 \\ Q_3 &= 8 \end{align}$
Simpangan kuartil ($Q_d$) adalah:
$\begin{align}Q_d &= \frac{1}{2}\left( Q_3-Q_1 \right) \\ &= \frac{1}{2}(8-4) \\ Q_d &= 2 \end{align}$
Jawaban: B
Soal No. 2
Diketahui data: 3, 5, 13, 15, 19, maka simpangan rata-rata data adalah ....A. 0
B. 3,6
C. 5,6
D. 11
E. 28
Penyelesaian: Lihat/Tutup
Rata-rata:$\begin{align}\bar{x} &= \frac{\sum{{{x}_{i}}}}{n};\,\text{untuk}\,i=1,2,3,...,n \\ &= \frac{3+5+13+15+19}{5} \\ \bar{x} &= 11 \end{align}$
Simpangan Rata-rata:

Jawaban: C
Soal No. 3
Diberikan sekumpulan data sebagai berikut: 7, 2, 3, 8, 4, 6. Nilai varians data di atas adalah ....A. 1
B. $\frac{7}{3}$
C. 2
D. $\frac{14}{3}$
E. 5
Penyelesaian: Lihat/Tutup
Rata-rata:$\bar{x}=\frac{7+2+3+8+4+6}{6}=5$
Varians:

Jawaban: D
Soal No. 4
Simpangan baku dari data 2, 3, 4, 5, 6 adalah ...A. $\sqrt{15}$
B. $\sqrt{10}$
C. $\sqrt{5}$
D. $\sqrt{3}$
E. $\sqrt{2}$
Penyelesaian: Lihat/Tutup
Rata-rata:$\bar{x}=\frac{2+3+4+5+6}{5}=4$
Varians ($S^2$):

Simpangan baku (S):
$S=\sqrt{\operatorname{varians}}=\sqrt{2}$
Jawaban: E
Soal No. 5
Pada suatu ujian yang diikuti oleh 50 siswa, diperoleh rata-rata nilai ujian adalah 35, median 40, dan simpangan baku 10. Karena rata-rata terlalu rendah, maka semua nilai dikalikan 2, kemudian dikurangi 15. Akibatnya ....A. rata-rata nilai menjadi 70
B. rata-rata nilai menjadi 65
C. simpangan baku menjadi 20
D. simpangan baku menjadi 5
E. median menjadi 50
Penyelesaian: Lihat/Tutup

Jawaban: C
Soal No. 6
Suatu data dengan rata-rata 16 dan jangkauan 6. Jika setiap nilai dalam data dikalikan $p$, kemudian dikurangi $q$ diperoleh data baru dengan rata-rata 20 dan jangkauan 9. Nilai dari $2p+q$ = ...A. 3
B. 4
C. 7
D. 8
E. 9
Penyelesaian: Lihat/Tutup

$\begin{align}6p &= 9 \\ p &= \frac{9}{6} \\ p &= \frac{3}{2} \end{align}$
$\begin{align}16p-q &= 20 \\ 16.\frac{3}{2}-q &= 20 \\ 24-q &= 20 \\ 24-20 &= q \\ 4 &= q \end{align}$
$2p+q=2.\frac{3}{2}+4=7$
Jawaban: C
Soal No. 7
Simpangan baku dari data 7, 7, 6, 11, 7, 5, 6, 7 adalah ....A. $\frac{1}{2}\sqrt{11}$
B. $\frac{1}{2}\sqrt{13}$
C. $\frac{1}{2}\sqrt{15}$
D. $\frac{1}{2}\sqrt{17}$
E. $\frac{1}{2}\sqrt{19}$
Penyelesaian: Lihat/Tutup
Rata-rata:$\bar{x}=\frac{7+7+6+11+7+5+6+7}{8}=7$
Varians:

Simpangan baku:
$S=\sqrt{\text{varians}}=\sqrt{\frac{11}{4}}=\frac{1}{2}\sqrt{11}$
Jawaban: A
Soal No. 8
Diketahui data: 4, 7, 10, 14, 15, maka simpangan rata-rata data adalah ....A. 0
B. 2
C. 3,6
D. 5,2
E. 10
Penyelesaian: Lihat/Tutup
Rata-rata:$\bar{x}=\frac{4+7+10+14+15}{5}=10$
Simpangan rata-rata:
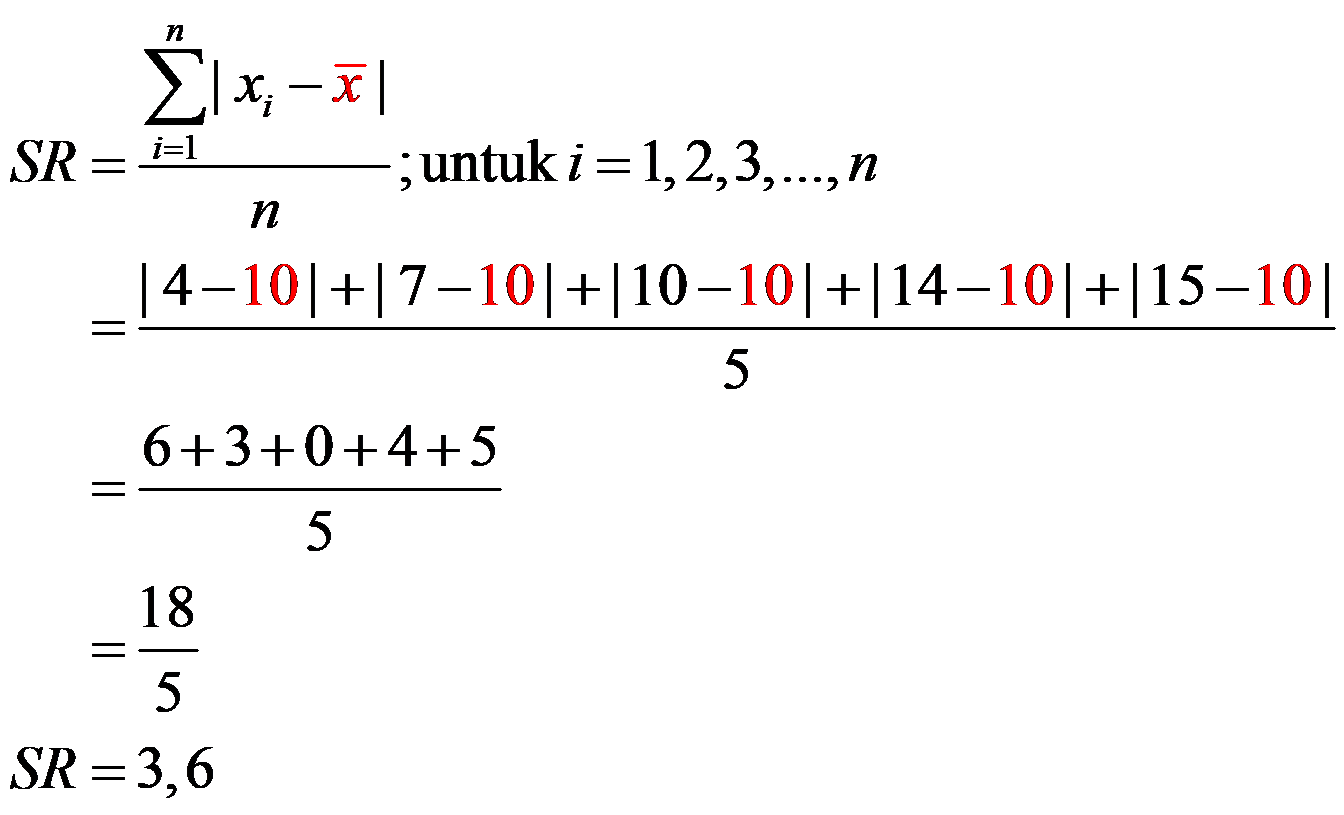
Jawaban: C
Soal No. 9
Pada suatu tes simulasi yang diikuti 50 siswa diperoleh nilai rata-rata matematika adalah 10. Karena nilai rata-rata terlalu rendah, maka semua nilai dikali 2, kemudian dikurangi 16. Jika nilai rata-rata yang baru sama dengan 2 kali simpangan baku yang baru, maka simpangan baku yang lama adalah ...A. 1
B. 2
C. 3
D. 4
E. 5
Penyelesaian: Lihat/Tutup

$\begin{align}\bar{x}_{baru} &= S_{baru} \\ 4 &= 2a \\ 2 &= a \end{align}$
Jadi, simpangan baku yang lama adalah ${{S}_{lama}}=a=2$.
Jawaban: B
Soal No. 10
Diketahui data 7, 10, 12, 15, 16, maka simpangan rata-rata data tersebut adalah ...A. 0
B. 1,8
C. 2
D. 2,8
E. 12
Penyelesaian: Lihat/Tutup
Rata-rata:$\begin{align}\bar{x} &= \frac{\sum{{{x}_{i}}}}{n};\,\text{untuk}\,i=1,2,3,...,n \\ &= \frac{7+10+12+15+16}{5} \\ \bar{x} &= 12 \end{align}$
Simpangan Rata-rata:

Jawaban: D
Soal No. 11
Simpangan baku dari data: 20, 20, 22, 24, 26, 24, 24, 28, 28 adalah ....A. $\frac{2}{3}\sqrt{5}$
B. $\frac{2}{3}\sqrt{11}$
C. $2\sqrt{2}$
D. $2\sqrt{5}$
E. $6\sqrt{2}$
Penyelesaian: Lihat/Tutup
Rata-rata:$\begin{align}\bar{x} &= \frac{2.20+22+3.24+26+2.28}{9} \\ &= \frac{216}{9} \\ \bar{x} &= 24 \end{align}$
Varians ($S^2$):

Simpangan baku (S):
$\begin{align}S &= \sqrt{\operatorname{varians}} \\ &= \sqrt{8} \\ S &= 2\sqrt{2} \end{align}$
Jawaban: C
Soal No. 12
Diketahui data terdiri dari 3 pengamatan mempunyai rata-rata 15, median 15, dan jangkauan 10. Data terbesar dari pengamatan tersebut adalah ....A. 18
B. 19
C. 20
D. 21
E. 22
Penyelesaian: Lihat/Tutup
Data: ${{x}_{1}}$, 15, ${{x}_{3}}$$\begin{align}\bar{x} &= \frac{x_1+15+x_3}{3} \\ 15 &= \frac{x_1+15+x_3}{3} \\ 45 &= x_1+15+x_3 \\ 30 &= x_1+x_3 \end{align}$
$\begin{align}J &= x_3-x_1 \\ 10 &= x_3-x_1 \end{align}$
$30={{x}_{3}}+{{x}_{1}}$
--------------------- +
$\begin{align}40 &= 2x_3 \\ 20 &= x_3 \\ \end{align}$
Jadi, data terbesar adalah 20.
Jawaban: C
Soal No. 13
Simpangan baku data 6, 4, 5, 6, 5, 7, 8, 7 adalah ....A. $\frac{1}{4}\sqrt{3}$
B. $\frac{1}{2}\sqrt{3}$
C. $\frac{1}{3}\sqrt{6}$
D. $\frac{1}{2}\sqrt{6}$
E. $2\sqrt{6}$
Penyelesaian: Lihat/Tutup
Rata-rata:$\begin{align}\bar{x} &= \frac{2.6+4+2.5+2.7+8}{8} \\ &= \frac{48}{8} \\ \bar{x} &= 6 \end{align}$
Varians ($S^2$):

Simpangan baku (S):
$\begin{align}S &= \sqrt{\operatorname{varians}} \\ &= \sqrt{\frac{3}{2}} \\ &= \frac{\sqrt{3}}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ S &= \frac{1}{2}\sqrt{6} \end{align}$
Jawaban: D
Soal No. 14
Suatu data mempunyai rata-rata 35 dan jangkauan 7. Jika setiap nilai dalam data dikali $p$ kemudian dikurangi $q$ di dapat data baru dengan rata-rata 42 dan jangkauan 9. Nilai $7p-q$ = ...A. 3
B. 4
C. 5
D. 6
E. 7
Penyelesaian: Lihat/Tutup

$7p=9\to p=\frac{9}{7}$
$\begin{align}35p-q &= 42 \\ 35.\frac{9}{7}-q &= 42 \\ 45-q &= 42 \\ 45-42 &= q \\ 3 &= q \end{align}$
$7p-q=7.\frac{9}{7}-3=6$
Jawaban: D
Soal No. 15
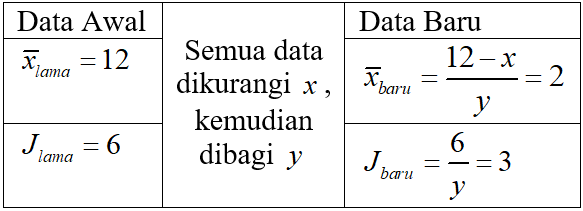
Sekumpulan data mempunyai rata-rata 12 dan jangkauan 6. Jika setiap data dikurangi dengan x kemudian hasilnya dibagi y ternyata menghasilkan data baru dengan rata-rata 2 dan jangkauan 3, maka nilai x + y adalah ....A. 8
B. 10
C. 12
D. 14
E. 16
Penyelesaian: Lihat/Tutup

$\begin{align}\frac{6}{y} &= 3 \\ 3y &= 6 \\ y &= 2 \end{align}$
$\begin{align}\frac{12-x}{y} &= 2 \\ \frac{12-x}{2} &= 2 \\ 12-x &= 4 \\ -x &= -8 \\ x &= 8 \end{align}$
$x+y=8+2=10$
Jawaban: B
Soal No. 16
Dari hasil ulangan 50 siswa, diperoleh nilai rata-rata 54 dan jangkauan 70. Karena nilai rata-ratanya terlalu rendah maka setiap nilai dikali 2 dan dikurangi 32. Nilai baru yang diperoleh mempunyai ...A. rata-rata 76, jangkauan 108
B. rata-rata 76, jangkauan 140
C. rata-rata 76, jangkauan 36
D. rata-rata 108, jangkauan 36
E. rata-rata 108, jangkauan 108
Penyelesaian: Lihat/Tutup

Jawaban: B

Post a Comment for "Soal Ukuran Penyebaran Data Tunggal - Simpangan Kuartil - Simpangan Rata-rata - Simpangan Baku - Varians dan Pembahasan"
Pertanyaan melalui kolom komentar akan direspon secepatnya. Jika tidak direspon, berarti pertanyaan serupa telah ada.