Solution of SEAMO 2017 Paper D

SEAMO (Southeast Asian Mathematical Olympiads)
SEAMO 2017 PAPER D

SEAMO 2017 Paper D No. 1

Find the value of $x$ in $\frac{x}{3+x}-\frac{x}{4-x}=2$.
A. $-12$
B. +12
C. $-24$
D. +24
E. +30

Solution: Show/Hide

$\begin{align}\frac{x}{3+x}-\frac{x}{4-x} &= 2 \\ \frac{x(4-x)-x(3+x)}{(3+x)(4-x)} &= 2 \\ \frac{4x-x^2-3x-x^2}{12-3x+4x-x^2} &= 2 \\ \frac{x-2x^2}{12+x-x^2} &= 2 \\ 24+2x-2x^2 &= x-2x^2 \\ x &= -24 \end{align}$
Answer: C

SEAMO 2017 Paper D No. 2

Find all positive value of $n$, such that ${{2}^{n}}-1$ is divisible by 7.
A. $n$ must be a multiple of 2
B. $n$ must be a multiple of 3
C. $n$ must be a multiple of 4
D. $n$ must be a multiple of 5
E. None of the above

Solution: Show/Hide

Consider $2^3=8\equiv 1(\bmod 7)$
The congruency holds for $k$ power.
$2^{3k}\equiv 1(\bmod 7)$
Thus, $n=3k$
Which is a multiple of 3.
Answer: B

SEAMO 2017 Paper D No. 3

Type A and B coffee are mixed in the ratio $m:n$ and costs $40 and $60 per kg, respectively. If the price of type A coffee is decreased by 15% while the price of type B coffee is increased by 15%, the total cost of the mixture remained unchanged. Find $m:n$.
A. 1 : 2
B. 2 : 3
C. 3 : 2
D. 2 : 1
E. 5 : 2

Solution: Show/Hide

$\begin{align}40m+60n &= 0.85\times 40m+1.15\times 60n \\ 40m+60n &= 34m+69n \\ 6m &= 9n \\ \frac{m}{n} &= \frac{9}{6} \\ \frac{m}{n} &= \frac{3}{2} \end{align}$
Answer: C

SEAMO 2017 Paper D No. 4

Evaluate $\frac{400^2\times (254^2+246^2)\times (254^4+246^4)}{(254^8-246^8)}$
A. 30
B. 40
C. 50
D. 60
E. 70

Solution: Show/Hide

$\frac{400^2\times (254^2+246^2)\times (254^4+246^4)}{(254^8-246^8)}$
= $\frac{400^2\times (254^2+246^2)\times (254^4+246^4)}{(254^4-246^4)(254^4+246^4)}$
= $\frac{400^2\times (254^2+246^2)}{(254^4-246^4)}$
= $\frac{400^2\times (254^2+246^2)}{(254^2-246^2)(254^2+246^2)}$
= $\frac{400^2}{254^2-246^2}$
= $\frac{{{400}^{2}}}{(254-246)(254+246)}$
= $\frac{400\times 400}{8\times 500}$
= 40
Answer: B

SEAMO 2017 Paper D No. 5

Evaluate $\frac{20172016^2}{20172015^2+20172017^2-2}$.
A. $\frac{1}{3}$
B. $\frac{1}{2}$
C. 1
D. $\frac{3}{2}$
E. None of the above

Solution: Show/Hide

$\frac{20172016^2}{20172015^2+20172017^2-2}$
Let $x=20172016$
$\frac{x^2}{{{(x-1)}^{2}}+{{(x+1)}^{2}}-2}$
= $\frac{x^2}{x^2-2x+1+x^2+2x+1-2}$
= $\frac{x^2}{2x^2}$
= $\frac{1}{2}$
Answer: B

SEAMO 2017 Paper D No. 6

It is known that $m=\frac{a}{b+c}=\frac{b}{a+c}=\frac{c}{a+b}$. Given that $a+b+c\ne 0$, find the value of $m$.
A. $\frac{1}{4}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. 1
E. None of the above

Solution: Show/Hide

Method 1:
We observe when $\frac{a_1}{b_1}=\frac{a_2}{b_2}=...=\frac{a_n}{b_n}$ given $a_1+a_2+...+a_n\ne 0$, then $\frac{a_1}{b_1}=\frac{a_2}{b_2}=...=\frac{a_n}{b_n}$ = $\frac{a_1+a_2+...+a_n}{b_1+b_2+...+b_n}$.
$\begin{align}m &= \frac{a+b+c}{b+c+a+c+a+b} \\ &= \frac{(a+b+c)}{2(a+b+c)} \\ m &= \frac{1}{2} \end{align}$
Method 2:
Let $a=b=c$
$\begin{align}m &= \frac{a}{b+c} \\ &= \frac{a}{a+a} \\ &= \frac{a}{2a} \\ m &= \frac{1}{2} \end{align}$
Answer: C

SEAMO 2017 Paper D No. 7

A rectangle is inscribed in a square as shown. It is known that the total area of 4 isosceles right angled $\Delta $ is 98 $\text{cm}^2$. Find $\text{XY}$, the length of the diagonal of rectangle.

A. 10
B. 11
C. 12
D. 13
E. 14

Solution: Show/Hide

Area of
$\begin{align}\Delta s &= 98 \\ \frac{1}{2}\times m^2\times 2+\frac{1}{2}\times n^2\times 2 &= 98 \\ m^2+n^2 &= 98 \end{align}$
$\begin{align}(\text{XY})^2 &= (m+n)^2+(m-n)^2 \\ &= m^2+2mn+n^2+m^2-2mn+n^2 \\ &= 2(m^2+n^2) \\ &= 2\times 98 \\ (\text{XY})^2 &= 196 \\ \text{XY} &= 14 \end{align}$
Answer: E

SEAMO 2017 Paper D No. 8

Evaluate $\left( \frac{2}{3}+\frac{3}{4}+...+\frac{49}{50} \right)$$\left( \frac{1}{2}+\frac{2}{3}+\frac{3}{4}...+\frac{48}{49} \right)$-$\left( \frac{1}{2}+\frac{2}{3}+\frac{3}{4}...+\frac{49}{50} \right)$$\left( \frac{2}{3}+\frac{3}{4}+...+\frac{48}{49} \right)$.
A. $\frac{49}{100}$
B. $\frac{99}{100}$
C. $\frac{49}{50}$
D. $\frac{48}{50}$
E. 1

Solution: Show/Hide

$\left( \frac{2}{3}+\frac{3}{4}+...+\frac{49}{50} \right)$$\left( \frac{1}{2}+\frac{2}{3}+\frac{3}{4}...+\frac{48}{49} \right)$-$\left( \frac{1}{2}+\frac{2}{3}+\frac{3}{4}...+\frac{49}{50} \right)$$\left( \frac{2}{3}+\frac{3}{4}+...+\frac{48}{49} \right)$
Let $x=\frac{2}{3}+\frac{3}{4}+...+\frac{48}{49}$
$\left( \frac{2}{3}+\frac{3}{4}+...+\frac{48}{49}+\frac{49}{50} \right)$$\left( \frac{1}{2}+\frac{2}{3}+\frac{3}{4}...+\frac{48}{49} \right)$-$\left( \frac{1}{2}+\frac{2}{3}+\frac{3}{4}...+\frac{48}{49}+\frac{49}{50} \right)$$\left( \frac{2}{3}+\frac{3}{4}+...+\frac{48}{49} \right)$
= $\left( x+\frac{49}{50} \right)\left( \frac{1}{2}+x \right)$-$\left( \frac{1}{2}+x+\frac{49}{50} \right)x$
= $\frac{1}{2}x+x^2$+$\frac{49}{100}$+$\frac{49}{50}x$-$\frac{1}{2}x$-$x^2$-$\frac{49}{50}x$
= $\frac{49}{100}$
Answer: A

SEAMO 2017 Paper D No. 9

Evaluate $\sqrt{2017+2016\sqrt{2017+2016\sqrt{2017+2016\sqrt{...}}}}$
A. 2015
B. 2016
C. 2017
D. 2018
E. 2019

Solution: Show/Hide

Let $x=\sqrt{2017+2016\sqrt{2017+2016\sqrt{2017+2016\sqrt{...}}}}$
Then,
$x=\sqrt{2017+2016x}$
$x^2=2017+2016x$
$x^2-2016x-2017=0$
$(x-2017)(x+1)=0$
$x=2017$
Answer: C

SEAMO 2017 Paper D No. 10

It is given that $a+\frac{1}{a}=5$, find $a^4+\frac{1}{a^4}$.
A. 523
B. 527
C. 631
D. 635
E. None of the above

Solution: Show/Hide

$a+\frac{1}{a}=5$
$\begin{align}\left( a+\frac{1}{a} \right)^2 &= 5^2 \\ a^2+2.a.\frac{1}{a}+\frac{1}{a^2} &= 25 \\ a^2+\frac{1}{a^2}+2 &= 25 \\ a^2+\frac{1}{a^2} &= 23 \end{align}$
$\begin{align}\left( a^2+\frac{1}{a^2} \right)^2 &= 23^2 \\ a^4+2.a^2.\frac{1}{a^2}+\frac{1}{a^4} &= 529 \\ a^4+\frac{1}{a^4}+2 &= 529 \\ a^4+\frac{1}{a^4} &= 527 \end{align}$
Answer: B

SEAMO 2017 Paper D No. 11

Evaluate ${{\log }_{\frac{1}{2}}}8+{{\log }_{2}}64-{{\log }_{5}}\frac{1}{125}$.
A. 2
B. 3
C. 4
D. 5
E. 6

Solution: Show/Hide

${{\log }_{\frac{1}{2}}}8+{{\log }_{2}}64-{{\log }_{5}}\frac{1}{125}$
= ${{\log }_{\frac{1}{2}}}{{\left( \frac{1}{2} \right)}^{-3}}+{{\log }_{2}}{{2}^{6}}-{{\log }_{5}}{{5}^{-3}}$
= $-3+6-(-3)$
= 6
Answer: E

SEAMO 2017 Paper D No. 12

ABCD is a rectangle with E the midpoint of AB and $DF\bot CE$. Given that AB = 6 and BC = 4. Find length of DF.

A. 3.6
B. 4.2
C. 4.8
D. 5.4
E. None of the above

Solution: Show/Hide

$\begin{align}CE &= \sqrt{BE^2+CB^2} \\ &= \sqrt{\left( \frac{AB}{2} \right)^2+CB^2} \\ &= \sqrt{3^2+4^2} \\ CE &= 5 \end{align}$
Area of rectangle ABCD = AD.CD
Area of $\Delta CDE$ = $\frac{1}{2}.AD.CD$
Area of rectangle ABCD = 2.$\Delta CDE$.
$\begin{align}AB.BC &= 2.\frac{1}{2}.DF.CE \\ 6\times 4 &= DF\times 5 \\ DF &= \frac{24}{5} \\ DF &= 4.8 \end{align}$
Answer: C

SEAMO 2017 Paper D No. 13

The smallest number which, when divided by 52 leaves a remainder 33, when divided by 78 leaves 59 as remainder and when divided by 117 leaves 98 as remainder is
A. 553
B. 293
C. 468
D. 449
E. 458

Solution: Show/Hide

52 – 33 = 19
78 – 59 = 19
117 – 98 = 19
It suffices to find the lowest common multiple of 52, 78, 117.

LCM is $13\times 3\times 2\times 2\times 1\times 3=468$.
468 – 19 = 449
Answer: D

SEAMO 2017 Paper D No. 14

In the figure shown below, the area of $\Delta ABC$ is 8 $\text{cm}^2$, AE = DE and BD = 2CD. Find the total area of the shaded regions.

A. 3.2 $\text{cm}^2$
B. 3.6 $\text{cm}^2$
C. 4.0 $\text{cm}^2$
D. 4.4 $\text{cm}^2$
E. None of the above

Solution: Show/Hide

$\frac{[BDF]}{[CDF]}=\frac{BD}{CD}=\frac{2}{1}$
$[CDF]=\frac{x+y}{2}$
[ABE] + [EBD] + [AEF] + [DEF] + [DFC] = [ABC]
$\begin{align}x+x+y+y+\frac{x+y}{2} &= 8 \\ 2x+2y+\frac{x+y}{2} &= 8 \\ 2(x+y)+\frac{1}{2}(x+y) &= 8 \\ \frac{5}{2}(x+y) &= 8 \\ x+y &= 8\times \frac{2}{5} \\ x+y &= 3.2\,\text{cm}^2 \end{align}$
Answer: A

SEAMO 2017 Paper D No. 15

In $\Delta ABC$, AN = BM = AB, $\angle C=38^\circ$. Find $\angle APB$.

A. $114^\circ$
B. $104^\circ$
C. $118^\circ$
D. $120^\circ$
E. $122^\circ$

Solution: Show/Hide

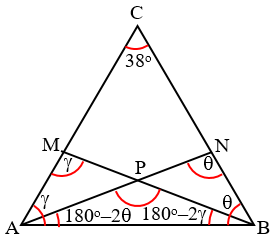
$\gamma +\theta =142^\circ$
$\begin{align}\angle APB &= 180^\circ -[360^\circ -2(\theta +\gamma)] \\ &= 180^\circ -[360^\circ -2\times 142^\circ] \\ &= 180^\circ -[360^\circ -284^\circ] \\ &= 180^\circ -76^\circ \\ &= 104^\circ \end{align}$
Answer: B

SEAMO 2017 Paper D No. 16

$p$ is the difference between a real number and its reciprocal. $q$ is the difference between the square of the same real number and the square of the reciprocal. The the value of $p^4+q^2+4p^2$ is
A. $2q^2$
B. $3q^2$
C. $\frac{1}{2}q^2$
D. $\frac{3}{4}q^2$
E. None of the above

Solution: Show/Hide

$q=x^2-\frac{1}{x^2}$
$\begin{align}p &= x-\frac{1}{x} \\ p^2 &= \left( x-\frac{1}{x} \right)^2 \\ p^2 &= x^2-2+\frac{1}{x^2} \end{align}$
$\begin{align}p^4+4p^2 &= (p^2+2)^2-4 \\ &= \left( x^2-2+\frac{1}{x^2}+2 \right)^2-4 \\ &= \left( x^2+\frac{1}{x^2} \right)^2-4 \\ &= x^4+2+\frac{1}{x^4}-4 \\ &= \left( x^4-2+\frac{1}{x^4} \right) \\ &= \left( x^2-\frac{1}{x^2} \right)^2 \\ p^4+4p^2 &= q^2 \end{align}$
$\begin{align}p^4+q^2+4p^2 &= p^4+4p^2+q^2 \\ &= q^2+q^2 \\ &= 2q^2 \end{align}$
Answer: A

SEAMO 2017 Paper D No. 17

A motorboat takes 6 h to travel from port A to port B, which is on the same side of the river. It takes the boat 8 h, to return to port A. It is given the speed of the current is 2.5 km/h. Find the speed of the boat in still water.
A. 10.5 km/h
B. 13.5 km/h
C. 16.5 km/h
D. 17.5 km/h
E. 18.5 km/h

Solution: Show/Hide

Time from port A to B: $t_1$ = 6 h
Time from port B to A: $t_2$ = 8 h
Speed of the current: $v_{current}$ = 2.5 h
Let:
$v_{boat}$ be the speed of the boat in still water (in km/h).
$d$ be distance between A and B (in km).
The boat’s relative speed:
Downstream (with the current):
$v_{down}=v_{boat}+v_{current}$
Upstream (against the current):
$v_{up}=v_{boat}-v_{current}$
Using the relationship:
distance = speed $\times $ time:
Downstream:
$\begin{align}d &= v_{down}.t_1 \\ &= t_1.\left( v_{boat}+v_{current} \right) \\ &= 6\left( v_{boat}+2.5 \right) \\ d &= 6v_{boat}+15\,....\,(1) \end{align}$
Upstream:
$\begin{align}d &= v_{up}.t_2 \\ &= t_2.\left( v_{boat}-v_{current} \right) \\ &= 8\left( v_{boat}-2.5 \right) \\ d &= 8v_{boat}-20\,....\,(2) \end{align}$
From equation (1) and (2):
$\begin{align}8v_{boat}-20 &= 6v_{boat}+15 \\ 2v_{boat} &= 35 \\ v_{boat} &= 17.5 \end{align}$
Answer: D

SEAMO 2017 Paper D No. 18

Given an equilateral triangle, what is the ratio of area of its inscribed circle to the area of its circumscribed circle?

A. 1 : 2
B. 1 : 3
C. 1 : 4
D. 1 : 5
E. None of the above

Solution: Show/Hide

$R=2r$
Area of its inscribed circle = $\pi r^2$
Area of its circumscribed circle = $\pi r^2$ = $\pi (2r)^2$ = $\pi .4r^2$
Ratio of tis inscribed circle to the area of its circumscribed circle is:
$\pi r^2:\pi .4r^2$ = 1 : 4
Answer: C

SEAMO 2017 Paper D No. 19

Arrange $3^{50}$, $4^{40}$, $5^{30}$ in ascending order.
A. $3^{50} < 4^{40} < 5^{30}$
B. $5^{30} < 3^{50} < 4^{40}$
C. $5^{30} < 4^{40} < 3^{50}$
D. $4^{40} < 5^{30} < 3^{50}$
E. None of the above

Solution: Show/Hide

$3^{50}=3^{5\times 10}=(3^5)^{10}=243^{10}$
$4^{40}=4^{4\times 10}=(4^4)^{10}=256^{10}$
$5^{30}=5^{3\times 10}=(5^3)^{10}=125^{10}$
$125^{10} < 243^{10} < 256^{10}$
$5^{30} < 3^{50} < 4^{40}$
Answer: B

SEAMO 2017 Paper D No. 20

Sara picks 2 oranges from a basket of 15 oranges in which 10 oranges are good, 5 oranges are bad. The probability that she picks up at least one good orange is $\frac{m}{n}$. Find the value of $(m+n)$.
A. 38
B. 39
C. 40
D. 41
E. 42

Solution: Show/Hide

$\begin{align}\frac{m}{n} &= \frac{C_1^{10}\times C_1^5+C_2^{10}}{C_2^5} \\ &= \frac{\frac{10!}{1!.9!}\times \frac{5!}{1!.4!}+\frac{10!}{2!.8!}}{\frac{15!}{2!.13!}} \\ &= \frac{\frac{10.9!!}{1.9!}\times \frac{5.4!!}{1.4!}+\frac{10.9.8!}{2.1.8!}}{\frac{15.14.13!}{2.1.13!}} \\ &= \frac{10\times 5+45}{105} \\ &= \frac{95}{105} \\ \frac{m}{n} &= \frac{19}{21} \end{align}$
$m+n=19+21=40$
Answer: C

SEAMO 2017 Paper D No. 21

In an equilateral $\Delta ABC$, D and E are points on BC and AB respectively. Given that BD = AE and AD and CE intersect at point F, find $\angle DFC$.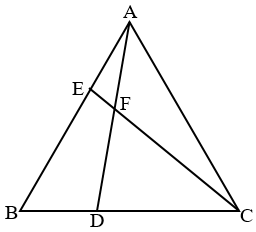

A. $30^\circ$
B. $36^\circ$
C. $42^\circ$
D. $54^\circ$
E. $60^\circ$

Solution: Show/Hide

$\angle A=\angle B=\angle C=60^\circ$
AB = BC = AC
In $\Delta ABD$ and $\Delta CAE$:
AB = AC
$\angle ABD=\angle CAE$
BD = AE (given)
$\therefore \Delta ABD\cong \Delta CAE$
Now, $\angle BAD+\angle DAC=\angle BAC=60^\circ$
$\angle ACE+\angle DAC=60^\circ$;
$\angle AFC=180^\circ -60^\circ =120^\circ$
$\begin{align}\angle DFC &= 180^\circ -\angle AFC \\ &= 180^\circ -120^\circ \\ &= 60^\circ \end{align}$
Answer: E

SEAMO 2017 Paper D No. 22

The number which, when subtracted from the terms of ratio $a:b$ makes it equal to $c:d$, is
A. $\frac{ab-cd}{ab+cd}$
B. $\frac{bc-ad}{c-d}$
C. $\frac{ab+cd}{c+d}$
D. $\frac{ab-cd}{b-c}$
E. None of the above

Solution: Show/Hide

$\frac{a-x}{b-x}=\frac{c}{d}$
Cross multiply:
$\begin{align}(a-x)d &= c(b-x) \\ ad-xd &= cb-cx \\ cx-dx &= cb-ad \\ x(c-d) &= cb-ad \\ x &= \frac{cb-ad}{c-d} \end{align}$
Answer: B

SEAMO 2017 Paper D No. 23

$a$, $b$, $c$ are three positive real numbers. $c$ is greater than $b$ by the amount that $b$ is greater than $a$. The product of the two smaller numbers is 85 and that of the two bigger numbers is 115. Then the value of $(2012a-1006c)$ is
A. 3355
B. 4433
C. 5533
D. 3344
E. 5454

Solution: Show/Hide

$a < b < c$
Let $a=A-D$, $b=A$, $c=A+D$
$\begin{align}\frac{(A-D)A}{A(A+D)} &= \frac{85}{115} \\ \frac{A-D}{A+D} &= \frac{17}{23} \\ 23A-23D &= 17A+17D \\ 6A &= 40D \\ 3A &= 20D \\ A &= \frac{20D}{3} \end{align}$
$\begin{align}(A-D)A &= 85 \\ \left( \frac{20D}{3}-D \right).\frac{20D}{3} &= 85 \\ \frac{17D}{3}.\frac{20D}{3} &= 85 \\ 17.20D^2 &= 9.85 \\ 4D^2 &= 9 \\ D^2 &= \frac{9}{4} \\ D &= \frac{3}{2} \end{align}$
$\begin{align}A &= \frac{20}{3}D \\ &= \frac{20}{3}.\frac{3}{2} \\ A &= 10 \end{align}$
$\begin{align}a &= A-D \\ &= 10-\frac{3}{2} \\ a &= \frac{17}{2} \end{align}$
$\begin{align}c &= A+D \\ &= 10+\frac{3}{2} \\ c &= \frac{23}{2} \end{align}$
$\begin{align}2012a-1006c &= 1006(2a-c) \\ &= 1006\left( 2.\frac{17}{2}-\frac{23}{2} \right) \\ &= 1006.\frac{11}{2} \\ &= 5533 \end{align}$
Answer: C

SEAMO 2017 Paper D No. 24

If $x=\frac{y}{y+1}$ and $y=\frac{a-2}{2}$, then value of $x(y+2)+\frac{x}{y}+\frac{y}{x}$ when $a=2017$ is
A. 2016
B. 2015
C. 2018
D. 2017
E. 2019

Solution: Show/Hide

$y=\frac{a-2}{2}$
$\begin{align}x &= \frac{y}{y+1} \\ &= \frac{\frac{(a-2)}{2}}{\frac{(a-2)}{2}+1} \\ x &= \frac{a-2}{a} \end{align}$
$\frac{x}{y}=\frac{\frac{a-2}{a}}{\frac{a-2}{2}}\to \frac{x}{y}=\frac{2}{a}$
$x(y+2)+\frac{x}{y}+\frac{y}{x}$
= $\frac{a-2}{a}\left( \frac{a-2}{2}+2 \right)+\frac{2}{a}+\frac{a}{2}$
= $\frac{a-2}{a}.\frac{a+2}{2}+\frac{4+a^2}{2a}$
= $\frac{a^2-4}{2a}+\frac{4+a^2}{2a}$
= $\frac{2a^2}{a}$
= $a$
= 2017
Answer: D

SEAMO 2017 Paper D No. 25

A triangular pyramid is made of 4 equilateral triangles as faces. If each side of equilateral triangular face is 1 unit, find the height of the pyramid.
A. $\sqrt{\frac{2}{3}}$
B. $\sqrt{\frac{3}{2}}$
C. $\frac{2}{\sqrt{3}}$
D. $\frac{\sqrt{3}}{2}$
E. None of the above

Solution: Show/Hide

$b=\frac{\sqrt{3}}{3}a$
Height of the pyramid : $H=\sqrt{a^2-b^2}$
$\begin{align}H &= \sqrt{a^2-\left( \frac{\sqrt{3}}{3}a \right)^2} \\ &= \sqrt{a^2-\frac{1}{3}a^2} \\ &= \sqrt{\frac{2}{3}a^2} \\ H &= a\sqrt{\frac{2}{3}} \end{align}$
$a=1$
$H=a\sqrt{\frac{2}{3}}=1.\sqrt{\frac{2}{3}}=\sqrt{\frac{2}{3}}$
Answer: A

Semoga postingan: Solution of SEAMO 2017 Paper D ini bisa bermanfaat. Mohon keikhlasan hatinya, membagikan postingan ini di media sosial bapak/ibu guru dan adik-adik sekalian. Terima kasih.

Share :